Main

Cavity optomechanical systems have emerged as an ideal testbed for exploring the quantum limits of linear measurement of macroscopic motion2, as well as a promising new architecture for performing quantum computations. In such systems, a light field reflecting off a mechanical oscillator acquires a position-dependent phase shift and reciprocally, it applies a force onto the mechanical oscillator. This effect is enhanced by embedding the oscillator inside a high-quality-factor electromagnetic cavity. Numerous physical implementations exist, both in the microwave and optical domains, and have been used to push the manipulation of macroscopic oscillators into the quantum regime, demonstrating laser cooling to the ground state of motion8,14, coherent transfer of itinerant light fields into mechanical motion9,15, or their entanglement10. Thus far, linear position measurements have provided evidence for the quantization of light fields through radiation pressure shot noise16,17 and mechanical vacuum fluctuations through motional sideband asymmetries4,5,6,7. However, the use of only classical and linear tools has restricted most optomechanical experiments to the manipulation of Gaussian states.

The addition of a strong nonlinearity, such as an atom, has fostered tremendous progress towards exquisite control over non-Gaussian quantum states of light fields and atomic motion11,12. First developed in the context of cavity quantum electrodynamics (cQED), these techniques are now widely applied to engineered systems, such as superconducting quantum bits (qubits) and microwave resonant circuits13,18,19,20,21. In a pioneering cQED-type experiment, a qubit resonantly coupled to a high-frequency mechanical oscillator3 allowed for the control of a single-phonon Fock state. However, short energy lifetimes of the mechanical oscillator and the qubit have slowed any further progress.

Here, we go beyond just cQED by introducing cavity optomechanical interactions. Our unique architecture incorporates an artificial atom—a superconducting qubit22—into a circuit cavity electromechanical system23, on a single chip. Here, a low-frequency, high-quality-factor mechanical oscillator strongly interacts with the microwave cavity photons. The qubit–cavity interaction realizes a non-classical emitter and detector of photons, thus providing an essential nonlinear resource for the deterministic control of long-lived mechanical quantum states. We demonstrate the potential of such an architecture by measuring the quantum vacuum fluctuations inherently present in the motion of a macroscopic oscillator.

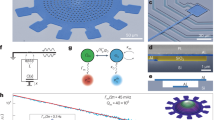
A microwave cavity is the central element of this architecture (in blue in Fig. 1a). It is a linear inductor–capacitor (LC) resonator formed by a coil inductor and a mechanically compliant vacuum-gap capacitor23,24. First, the intra-cavity electromagnetic field is coupled by means of radiation pressure to the vibrational mode of the compliant capacitor (in red in Fig. 1). Second, the microwave cavity is capacitively coupled to a phase qubit (in green in Fig. 1). A phase qubit is formed from a Josephson junction in parallel with an LC oscillator, and it behaves like a nonlinear resonator at the single-quantum level, that is, an artificial atom22. To a good approximation the phase qubit can be operated as a two-level system whose transition frequency ωqb can be widely tuned in situ by applying an external flux, such that 9 GHz ≤ ωqb/2π ≤ 13.5 GHz. The microwave cavity and the fundamental flexural mode of the capacitor are two harmonic oscillators with resonance frequencies of respectively ωc/2π = 10.188 GHz and Ωm/2π = 15.9 MHz.

Figure 1: Device description and strong-coupling regime.
figure 1

a, False-colour optical micrograph of the device. Aluminium is in grey and sapphire in light blue. The phase qubit is in green; the microwave cavity in blue; and the mechanically compliant capacitor in red. b,c, False-colour scanning electron micrograph of the qubit’s Josephson junction and of the mechanical oscillator, respectively. d, Equivalent circuit diagram. e, Qubit–cavity vacuum Rabi splitting. Population of the qubit’s excited state Pe, in green, as a function of the drive frequency and of the qubit detuning with respect to the microwave cavity. The avoided crossing is a clear signature of the single-photon strong-coupling regime. From a fit with theory we extract the qubit/cavity coupling rate J/2π = 12.5 MHz. f, Cavity–oscillator normal-mode splitting. Reflected power in blue as a function of the drive and pump frequencies. The drive is applied near the cavity resonance and the pump is applied near Δp = −Ωm. Here, the pump strength is set to np ≈ 5 × 105. The normal-mode splitting observed in the cavity-driven response corresponds to the hybridization of the cavity and mechanical modes in the driven strong-coupling regime. From a fit with theory we extract κ/2π = 163 kHz, Γm/2π = 150 Hz and , where at T ≈ 25 mK.

Full size image

The qubit and the cavity are both electrical circuits with quantized energy levels, sharing a voltage through the coupling capacitor. On resonance, Δqb = ωqb − ωc = 0, the interaction between the qubit and the cavity is well described by the Jaynes–Cummings Hamiltonian . Here, () is the raising (lowering) operator for the qubit, () is the creation (annihilation) operator for cavity photons and J is the capacitive coupling strength. describes the exchange of a single quantum between the qubit and the cavity at a rate 2J. In the strong-coupling regime, when the coupling strength J overcomes the decoherence rates of the qubit γqb and the cavity κ, that is, J > (γqb, κ), the system hybridizes, leading to the well-known vacuum Rabi splitting, measured spectroscopically in Fig. 1e. The qubit–cavity interaction can be effectively turned off by detuning the qubit.

The position of the mechanical oscillator modulates the cavity resonance frequency and thus, the energy stored in the cavity. As a result, the microwave photons apply a force on the mechanical oscillator. This interaction is described by the radiation pressure Hamiltonian2 , where G = dωc/dx, is the cavity photon number and is the oscillator’s position. Here, xzpf is the oscillator’s zero-point fluctuation and () is the creation (annihilation) operator for mechanical phonons. The force applied by a single photon onto the mechanical oscillator is typically weak, with , where is the equilibrium thermal occupancy of the oscillator and Γm is its intrinsic relaxation rate. However, the total force increases significantly with the intensity of the intra-cavity field. In the presence of a strong coherent microwave pump of frequency ωp, the optomechanical interaction is linearized and takes two different forms depending on the pump–cavity detuning Δp = ωp − ωc (Supplementary Information). When Δp = − Ωm, the annihilation of a mechanical phonon can up-convert a pump photon into a cavity photon, mediating a ‘beamsplitter’ interaction, . This results in the coherent exchange of the cavity and mechanical states at a rate 2g, where is the enhanced optomechanical coupling and np is the pump strength expressed in terms of the average number of intra-cavity photons. When Δp = + Ωm, pump photons are down-converted into correlated photon–phonon pairs, mediating a ‘two-mode squeezer’ interaction, . This results in the amplification and entanglement of the cavity field and the mechanical motion10, at a rate 2g. The hallmark for entering the strong-coupling regime in our device, g > (Γm, κ), is the hybridization and normal-mode splitting induced by a strong beamsplitter interaction23, as measured through the cavity-driven response in Fig. 1f. Finally, with a lifetime of the mechanical oscillator’s ground state, μs, much longer than the cavity lifetime, 1/κ ≈ 1 μs, this device is in the quantum-coherent regime15.

Measurements in the frequency domain provide an extensive characterization of the device’s parameters; however, they probe only the steady state of the system, in equilibrium with the thermal environment. In the next two paragraphs, we will show that time-domain protocols enable: the preparation of non-classical cavity states and the measurement of the intra-cavity photon-number distribution11,12,13; and coherent state transfer by frequency conversion and entanglement by parametric amplification between the microwave cavity and the mechanical oscillator25,26.

The out-of-equilibrium dynamics between the phase qubit and the cavity are shown in Fig. 2. First, in Fig. 2a, b we perform the first basic block of the Law–Eberly protocol27. We initialize the qubit in the excited state using a resonant microwave pulse, then tune the qubit into resonance with the cavity for an interaction time τ and measure the qubit population Pe (using a destructive single-shot readout). The coupled system undergoes vacuum Rabi oscillations at a single frequency J/π and after half a cycle the cavity is prepared in a single-photon Fock state. Next, in Fig. 2c–f, we exploit the well-known scaling of the Rabi frequency with the cavity Fock state number to measure the intra-cavity photon-number distribution13. We initialize the cavity in either a coherent state or a thermal state, parametrized by the average photon occupancy . When the qubit is tuned into resonance, each initial distribution (Fig. 2d) produces a distinct time evolution of Pe(τ) (Fig. 2e, f), in good agreement with simulations that include all sources of decoherence and where the average photon number is the only free parameter (Supplementary Information). We resolve the cavity occupancy down to and have the ability to distinguish the thermal, noise-like component of the cavity state from the coherent component.

Figure 2: Cavity state preparation and readout.
figure 2

a, Sequence diagram for the preparation of a single-photon Fock state in the cavity. The qubit is prepared in the first excited state |e〉, with a 75% efficiency, and then interacts resonantly with the cavity for a time τ before the qubit state is measured. b, The population of the qubit Pe plotted as a function of the interaction time τ. The black line is a fit to a master equation prediction (Supplementary Information). c, Sequence diagram for the readout of the cavity state. The cavity is prepared in a coherent (or thermal) state by driving it with a coherent tone (or with white noise). d, The corresponding intra-cavity photon distributions for four drive amplitudes, parametrized by the average cavity occupancy . The distributions for thermal and coherent states are respectively in bright and dark blue. e,f, For each drive amplitude, the evolution of the qubit population Pe is plotted in green for the coherent states (e), and for the thermal states (f). The solid lines are a fit to a master equation prediction.

Full size image

We will now exploit this measurement technique to explore the out-of-equilibrium optomechanical dynamics (Fig. 3). To acquire some physical intuition one can solve the lossless equations of motion describing the time evolution of the microwave and mechanical field amplitudes (Supplementary Information). The average photon occupancy after a beamsplitter interaction, , or a two-mode squeezer interaction, , follows:

where and are respectively the initial cavity and mechanical occupancy, and θ = ∫ 2g(t) dt is the accumulated interaction phase. The periodic functions in equation (1) describe the state exchange induced by the beamsplitter interaction (see Fig. 3b) and the hyperbolic functions in equation (2) describe the amplification induced by the two-mode squeezer interaction (see Fig. 3c). Experimentally, we start by actively preparing the mechanical state in a nearly pure coherent state, , where |αmi| 2 = 23 is the coherent component (displacement) and represents the residual thermal (incoherent) phonon occupancy (Supplementary Information). We then pulse either optomechanical interaction using a microwave pump at Δp = ±Ωm, followed by tuning the qubit into resonance with the cavity to measure the subsequent photon-number distribution (as described previously in Fig. 2) for each pump duration. As expected this distribution corresponds to a displaced thermal state, characterized by an incoherent component and a coherent component αc±, for a total average photon occupancy of . In Fig. 3b, c, we show as a function of the interaction phase θ. The data in Fig. 3b (Fig. 3c) qualitatively agree with equation (1) (equation (2)), and quantitatively agree with full numerical simulations (solid blue lines) that include the finite linewidth and bath temperature of each mode (Supplementary Information). The expected evolution of follows the solid red line. The only free parameter is the initial mechanical occupancy . We emphasize our ability to resolve, with a sensitivity well below the single-quantum level, the coherent exchange of mechanical phonons and cavity photons or the amplification of the two localized modes, with both processes occurring at a rate faster than decoherence.

Figure 3: Optomechanics with a number-resolving detector.
figure 3

a, Sequence diagram. b, Measured cavity occupancy (blue circles) as a function of the interaction duration in reduced unit θ, for Δp = −Ωm (np = 3.8 × 105 and g = 2π × 198 kHz). c, The same as in b for Δp = +Ωm. In both b and c the predictions of the Heisenberg–Langevin equations of motion are shown in solid blue lines (Supplementary Information). The mechanical occupancy is shown as solid red lines. d, Measurement of the vacuum fluctuations of the mechanical oscillator. The cavity occupancy is measured as a function of the initial mechanical displacement for θ = π and for Δp = ±Ωm. The gain at each pump frequency, G±, is the ratio of final cavity displacement to initial mechanical displacement G± = |αc±| 2/ |αmi| 2, which is constant for all αmi. We show 〈â†â〉−/G− in red and 〈â†â〉+/G+ in blue. The amplification of the mechanical vacuum fluctuations appears as one additional quantum when Δp = +Ωm. The error bars are the measurement uncertainty of the photon-number distribution (Supplementary Information).

Full size image

A striking signature of the quantum nature of the oscillator’s motion resides in the commutation relation . Together with equation (2), we can see that even with both modes initially in their ground state, , the zero-point motion of the oscillator alone feeds the parametric amplification process, with a gain sinh2(θ/2), leading to a finite cavity occupancy . In contrast, from the same initial conditions, equation (1) shows no interesting dynamics for the beamsplitter interaction, with . Thus, to quantitatively extract the ‘+1’ contribution during amplification, we compare the two processes, as shown in Fig. 3d. With the cavity initially in its ground state, , equation (1) and equation (2) relate the final average cavity occupancy to the initial average mechanical occupancy through the gain of the parametric interactions, sin2(θ/2) for the beamsplitter or sinh2(θ/2) for the two-mode squeezer. First, we set the interaction phase to θ = π and measure the final photon distribution as a function of the initial mechanical displacement αmi, for Δp = +Ωm and Δp = −Ωm. In the presence of loss, both gains are less than their maximum values, G− < sin2(π/2) and G+ < sinh2(π/2). By taking the ratio of final cavity displacement to initial mechanical displacement, G± = |αc±| 2/ |αmi| 2, we measure G− = 0.25 and G+ = 0.88, at all coherent drive amplitudes (Supplementary Information). We show the results for in red and in blue. The difference between these two optomechanical interactions is clear in Fig. 3d, showing the extra ‘+1’ contribution sourced directly from the commutator between the position and momentum of the macroscopic mechanical oscillator due to the quantum vacuum fluctuations.

This signature has been discussed in terms of asymmetry between the rates of phonon absorption and emission5,7, or in terms of added noise in the context of three-wave mixing1,28. Our architecture is however uniquely suited to explore quantitatively this phenomenon in optomechanics, because we have the ability to measure directly the mechanically scattered photons, localized in the cavity. By combining the measurement of the intra-cavity photon-number distribution with the optomechanical interactions, we have realized a phonon-number distribution measurement. The nonlinearity of the qubit–cavity interaction allows us to clearly distinguish classical noise from quantum noise, as only classical noise can lead to real cavity quanta that can excite the qubit out of its ground state. In addition, our technique is not sensitive to the correlations between the electromagnetic noise and mechanical noise, which would induce ‘squashing’ of the output field7.

Looking forward, with more complex protocols, we could: exploit the qubit as a deterministic single-phonon source to generate arbitrary quantum states of motion20; perform full-state tomography of the mechanical oscillator29. The ability to encode complex quantum states in these long-lived mechanical systems has important implications for quantum information and for the study of the fundamental quantum behaviour of massive objects30.