Observation of the kinetic condensation of classical waves

Abstract

The observation of Bose–Einstein condensation, in which particle interactions lead to a thermodynamic transition into a single, macroscopically populated coherent state, is a triumph of modern physics^1,2,3,4,5. It is commonly assumed that this transition is a quantum process, relying on quantum statistics, but recent studies in wave turbulence theory have suggested that classical waves with random phases can condense in a formally identical manner^6,7,8,9. In complete analogy with gas kinetics, particle velocities map to wavepacket k-vectors, collisions are mimicked by four-wave mixing, and entropy principles drive the system towards an equipartition of energy. Here, we use classical light in a self-defocusing photorefractive crystal to give the first observation of classical wave condensation, including the growth of a coherent state, the spectral redistribution towards equilibrium, and the formal reversibility of the interactions. The results confirm fundamental predictions of kinetic wave theory and hold relevance for a variety of fields, ranging from Bose–Einstein condensation to information transfer and imaging.

Main

Weakly interacting bosons may exhibit, under extremely low temperatures, a Bose–Einstein transition^1,2,3,4,5. This transition is characterized by a macroscopic occupation of the ground state. The quantum nature of the bosons involved is crucial for this process, and indeed Bose–Einstein condensation (BEC) is a wonderful manifestation of quantum mechanics at a macroscopic scale. On the other hand, a growing body of theoretical work has predicted that completely classical waves may undergo an analogous condensation process^6,7,8,9. The requirements are a random ensemble of waves, so that statistical arguments apply, and a means of interaction between modes. Examples include sea waves stirred by wind, vibrations on elastic plates, interacting oscillators, and diffracting light that propagates in a nonlinear medium^6,10,11. As these systems evolve, turbulent wave mixing leads to a self-organized redistribution of energy: an inverse cascade increases the ‘number of waves’ in the lowest allowed mode while a normal cascade transfers energy towards higher momenta. The process is ruled by the natural thermalization of a conservative Hamiltonian wave system. As with the collisions of particles, each wave interaction is formally reversible, yet entropy principles mandate that the ensemble evolves towards an equilibrium state of maximum disorder. In this way, a large-scale coherent structure grows and becomes immersed in a sea of small-scale fluctuations (‘uncondensed particles’), which store the information necessary for reversible evolution of the waves. Here, we directly observe this process of wave condensation, as well as its formal reversibility, by imaging classical light dynamics in a photorefractive crystal.

As in ordinary kinetic theory, wave dynamics can often be expressed as a hierarchy of interaction processes. Known as wave turbulence theory^{10,11,12,13,14,15}, this approach focuses on the spectral distribution of modes as the field ψ(x,y,z) evolves. We apply the theory here to the nonlinear propagation of an optical beam, where ψ describes the envelope of the electric field and the dynamics occur in the x–y plane as the field propagates along z. To consider the interaction of modes, we concentrate on the (ensemble-averaged) power spectrum n(k,z), defined through , where is the Fourier transform of ψ(x,y,z) and * denotes complex conjugation. Formally, following this quantity results in an infinite hierarchy of moment equations. However, the hierarchy can be closed if the interactions are sufficiently weak (the ‘gas’ is sufficiently dilute), so that low-order collisions dominate. For example, for systems in which four-wave mixing is the dominant interaction, the evolution of n(k,z) follows the Boltzmann-like kinetic equation^{10,11,13,14,15}

where g is the strength of the nonlinear interaction, $n_{{\text{k}}_i}$ is shorthand for n(k_i,z), and W₀ = σ δ(k₁+k₂−k₃−k₄)δ(k₁²+k₂²−k₃²−k₄²) is the collision term. In this latter term, σ = σ(k₁,k₂,k₃,k₄) is a scattering matrix, which in general depends on the complete set of k vectors, and the Dirac delta functions ensure the conservation of momentum and energy. For many systems, including and especially the homogeneous optical system considered below, σ reduces to a simple constant factor. This scalar form is therefore foundational, in the same sense that hard sphere or s-wave models form the basis of more complex theories¹⁶.

In complete analogy with Boltzmann’s equation, the kinetic wave equation is not reversible with respect to the propagation variable z. This happens despite the reversibility of the individual interactions, due to the truncation of higher-order terms and the averaging of the overall dynamics^14,15. Formally, this is expressed by the H-theorem of entropy growth dS/dz≥0, where the nonequilibrium entropy reads . The equilibrium spectrum n^eq(k) is determined from the condition of zero entropy growth (maximum entropy¹¹). One obtains the celebrated Rayleigh–Jeans distribution for classical nonlinear waves:

where k²/2k_L may be regarded as the (transverse) kinetic energy of waves with wavelength 2π/k_L and the parameters 1/T and −μ/T are Lagrange multipliers introduced to ensure conservation of energy and power (‘particle number’) . By analogy with thermodynamics, we call T the temperature and μ the chemical potential of the system. Interestingly, the one-to-one correspondence between {N,E} and {μ,T} implies that the field evolution can be described in the framework of the microcanonical statistical ensemble^8,9 (in contrast with the canonical treatment using a thermal bath¹⁶). In what follows, we will use both sets of variables interchangeably.

The equilibrium distribution (2) is a Lorentzian spectrum, with statistics characterized by the correlation length . The correlation length diverges as μ →0, indicating that in an infinite system the k = 0 (‘plane-wave’) mode become macroscopically populated. In two dimensions, however, the requirements of finite temperature, density and energy mean that condensation can occur only in bounded systems^8,9,17; in this case, waves accumulate in the lowest available wavenumber k₀≠0 as μ→μ_c = k₀²/2k_L. The other ‘excited’ waves occupy an algebraic k⁻² spectrum, given by the tails of the distribution (2), indicating that there is an equipartition of energy among the uncondensed modes. For the experiment, a relatively large beam size was chosen (3 mm diameter), so that beam spreading was negligible over the length of the crystal. The surface area S of the beam thus bounds the region of wave interactions, and the system evolves with statistically homogeneous fluctuations (consistent with a basic assumption of wave turbulence theory). For the circular beam, the fundamental mode is characterized by , where is the first zero of the Bessel function J₀(r). More details are given in the Supplementary Information.

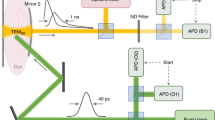
We realize the condensation of classical waves experimentally using the set-up shown in Fig. 1. A finite-size, 10 mW beam is projected onto two sequential spatial light modulators (SLMs). The SLMs create a random-phase field (taken from a Gaussian (Maxwell–Boltzmann) distribution) with a user-defined correlation length l_c. Nonlinear wave action occurs in a 5×5×10 mm SBN:75 (Sr_0.75Ba_0.25Nb₂O₆) photorefractive crystal with a self-defocusing (repulsive) coupling strength g controlled by applying a voltage across the c axis¹⁸. Output from the crystal is then imaged directly in both position (x) and momentum (k) space.

Figure 1: Experimental set-up.

Light from a 532 nm laser is collimated onto intensity and phase spatial light modulators (SLMs). The beam is modulated with a random intensity and phase pattern and imaged onto the input plane of a SBN:75 crystal. The output is observed using real (x) space and Fourier (k) space cameras. A piezo-electric actuator is used to shift the reference beam in increments of λ₀/4. Note: for the purpose of clarity, imaging lenses are not shown and the spatial light modulators are shown as transmissive, instead of reflective as in the actual experiment.

The condensation of classical waves is shown in Figs 2, 3, 4. Figure 2 shows experimental pictures when the nonlinear coupling strength is fixed at −500 V and the energy per particle E/N is varied. As the initial kinetic energy decreases, waves accumulate in the mode with the largest available spatial scale. Considering that the initial input beam was centred around k = 0, all modes with spatial frequencies belong to the condensate mode. Using the base width of the spectral peaks in Fig. 2d,e as the characteristic wavenumber scale, the measured value of k₀ = 2×10⁻³ μm⁻¹ matches very well with the theoretical prediction. The approach to this value as condensation progresses is seen more clearly by considering the corresponding chemical potential, plotted in Fig. 3a.

Figure 2: Condensation results as a function of decreasing kinetic energy (increasing correlation length).

a–e, Real-space (top row) and k-space (bottom row) intensity pictures for initial wave kinetic energies E/N of 13.3 (a), 10.4 (b), 7.1 (c), 4.6 (d) and 1.8m⁻¹ (e). The nonlinear interaction strength is fixed by maintaining a constant applied voltage bias of −500 V.

Figure 3: Approach to equilibrium and condensation.

Shown are results for fixed interaction strength, obtained by maintaining a constant voltage of −500 V across the crystal. a,b, Chemical potential (a) and condensate fraction (b) versus energy per particle E/N. Dots are experimental values, obtained from an average over 10 runs, while solid lines are theoretical fits. Error bars show variance. The red line in b corresponds to the limit μ→μ_c = k₀²/(2k_L), in which the fundamental Bessel mode k₀ becomes macroscopically populated. The blue line takes into account finite-size effects, (see Supplementary Information). c,d, Spectral profiles of random-phase input (black line) and equilibrium output (red, blue lines) from numerical simulation (c) and experimental measurements (d). The green line in c is a reference k⁻² spectrum predicted from Rayleigh–Jeans theory. Inset in d is a least-squares fit of the experiment.

Figure 4: Condensation results as a function of increasing interaction strength.

a–g, Real-space (top row) and k-space (bottom row) intensity pictures at input (a), linear output (b), −100 V (c), −200 V (d), −300 V(e), −400 V (f) and −500 V(e). The power N and correlation length are kept constant, so that the growth of the condensate is due to an increase in nonlinear coupling strength.

The amount of light in the condensate can be determined by a mode-counting argument. To do this, we limit the wavenumber range to , where the ultraviolet cut-off k_D corresponds to the Debye length in the photorefractive crystal (∼2 μm). Following the usual interpretation of BEC, we separate the ground state contribution from that of the ‘excited states’¹⁶. In the limit μ→μ_c = k₀²/2k_L, n_k^eq exhibits a divergence, showing that the fundamental mode k₀ becomes macroscopically populated. The fraction of condensed power follows directly from equation (2) (a detailed derivation is given in the Supplementary Information) and reads , where N_*is the number of modes and E₀ = N k₀²/2k_L refers to the lowest energy, that is the energy of the optical field when all quasi-particles occupy the ground state. Condensate fractions for μ = μ_c and μ≠μ_c are plotted in Fig. 3b. We note that the dynamics follows the ideal limit over most of the observed energy range, despite the finite size of the beam.

According to equation (2), the equilibrium state should be a Rayleigh–Jeans spectrum. Numerical and experimental proof of this is given in Fig. 3c,d respectively. The figures show explicitly the conservative nature of the spectral redistribution, with modes at both low and high wavenumbers growing at the expense of those in the middle of the range. This bidirectional energy transfer is required by the formal reversibility of the wave condensation process: as waves condense into the fundamental mode, information about their progress is recorded in the dynamics of the uncondensed, high- k modes^8,9,19,20.

Nonlinear interactions are necessary for condensation to occur. Figure 4 shows experimental pictures when the initial kinetic energy is fixed (l_c = 200 μm) while the nonlinear wave coupling (applied voltage) is increased. For linear propagation, the output spectrum (Fig. 4b) is statistically similar to the input spectrum (Fig. 4a). As the nonlinearity is increased (Fig. 4c–g), the spectrum concentrates in the fundamental k₀≈0 mode. This mode reached a steady-state height at approximately −400 V, verifying that changing the interaction strength only changes the rate, not the asymptotic state, of the condensation process.

We emphasize that the observed spectral redistribution and condensation of light arises spontaneously from the natural thermalization of the conservative wave system. This contrasts with the familiar case of blackbody radiation, in which interaction with cavity walls prevents photon condensation from taking place^5,21. The thermalization also contrasts with similar wave dynamics observed in other systems, such as optical mode coupling/locking in lasers^22,23 and self-focusing turbulence in liquid crystals²⁴, which are inherently dissipative systems driven far from equilibrium. In a similar way, optical wave thermalization through supercontinuum generation is affected by the dissipative Raman effect²⁵. We note, in particular, that although wave turbulence theory is independent of the sign of the interactions¹¹, in practice modulation instability dominates in the self-focusing case; the dynamics are controlled by the potential (rather than kinetic) energy of the system, the (inverse) momentum cascade is unidirectional, self-similar spectra are transient, and ‘condensation’ appears in the form of coherent soliton structures^24,26. Localized intensity structures (zeros in the field) are present here from the random-phase initial conditions, but these did not participate actively in the dynamics. We did not observe waveguide filtering from each zero²⁷ or an increase in their number during propagation, for example from vortex unbinding in a Berezinskii–Kosterlitz–Thouless transition¹⁶.

For long propagation distances (analogous to long evolution times), dynamics should consist of fluctuations around the equilibrium state. Unfortunately, the finite length of the crystal inhibits a direct measurement of this. Indeed, all nonlinear propagation experiments are limited by the finite extent of their media. To get around this, we introduce a novel feedback mechanism which takes advantage of the digital nature of our input/output devices (Fig. 1): the output field is recorded in the CCD (charge-coupled device) cameras and then used as the input field of the SLMs. This field recycling creates an effectively infinite crystal, subject to discretization errors, band-pass filtering, and bit-depth limitations. After a second pass through the crystal, the peak of the condensate remains within 10% of the single-pass value (with a correlation coefficient of 0.95 between the two spectral profiles). These results, in combination with longer-propagation simulations (Fig. 3c), confirm that the optical field has reached a (quasi-) equilibrium state.

The feedback method enables a scenario not possible in classical gas dynamics: selective and controlled adjustment of each particle’s momentum. To show reversibility, we change the sign of all the particle velocities; in the wave case, this is achieved by phase conjugation. As shown in Fig. 5b, the SLM can act as an ideal ‘Maxwell demon,’²⁸ reversing the flow of condensation and recovering the initial ‘thermal’ cloud (with a correlation coefficient of 0.88). This experimentally proves that although the ensemble dynamics described by equation (1) always evolves towards maximum entropy, the individual wave collisions are formally reversible (conservative); as wavepackets collapse, the uncondensed ones retain all the information necessary to reconstruct the dynamical history.

Figure 5: Digital feedback, showing a steady-state condensate in the forward direction and reversible behaviour in the backward direction.

The digital output recorded in the CCD cameras is fed back into the spatial light modulator (SLM) and used directly as input (a) or digitally phase-conjugated and then recycled through the crystal (b). In a the condensate remains constant after a second round of forward propagation; whereas in b the condensate reverts back to the initial ‘thermal’ cloud after propagation backwards.

The dynamics has interesting consequences when the waves have signal content. For example, recent methods of imaging using spatial nonlinearity have shown that wave mixing can greatly increase signal coherence²⁹ and resolution¹⁹ while the information content of the system remains constant. More generally, information capacity is defined by entropy, yet the ability to reach capacity and the corresponding transmission dynamics are typically treated as separate issues²⁸. Here, we have demonstrated that nonlinear interactions link the parameters of propagating beams, with entropy both constraining and driving the thermodynamics of classical waves.

Methods

The initial condition consists of a random-phase beam with Gaussian statistics and a correlation length l_c = 2π/Δk:

where is delta-correlated. This input approximates a Maxwell–Boltzmann distribution and, in particular, ensures that all initial odd moments are zero (necessary to maintain a zero mean field). Inside the nonlinear crystal, the slowly varying field ψ obeys the Schrödinger equation , where the photorefractive screening nonlinearity Δn = −(1/2)n₀³r_{i j}E₀(I/1+I) (ref. 18). In this expression, n₀ = 2.3, r_{i j}is the electro-optic coefficient, I = |ψ|² is in units of background illumination, and E₀ is generated by applying a bias across the crystal. At the maximum applied voltage of −500 V, the nonlinear index change is measured to be Δn/n₀ = −6.4×10⁻⁴. These experimental parameters were used for the numerical results in Fig. 3c, obtained by direct simulation of the Schrödinger equation for a spatially confined speckle beam of radius 1.5 mm (using a numerical grid of 1,024×1,024 points and an average over 20 realizations).

The real and Fourier space intensity at the output face of the crystal are imaged using CCD cameras. Phase information is retrieved experimentally using a phase shifting algorithm³⁰, where the reference beam is shifted using a piezo-actuated mirror in increments of λ₀/4±5 nm. The range of the cameras is limited to 12 bits. In Fig. 3d, the output power spectrum was measured using a series of different intensity filters, re-scaled and summed together to produce the entire power spectrum over 4.5 decades of intensity (2.7 decades of wavenumber). However, the input power spectrum was Gaussian only within two decades of intensity, below which it deviates from a quadratic falloff. Despite this, the system dynamically self-adjusts to the asymptotic k⁻² spectrum over the full recorded range.