Main

Superconducting states with non-zero orbital angular momentum, , are characterized by a competitive, but essential, relationship with magnetism, strong normal-state anisotropy or both1,2,3,5. Moreover, these states are strongly suppressed by disorder, an important consideration for applications7 and a signature of their unconventional behaviour3,8,9. Although liquid 3He in its normal phase is perfectly isotropic, it becomes a p-wave superfluid at low temperatures with non-zero orbital and spin angular momenta, L=S=1 (ref. 10). One of its two superfluid phases in zero magnetic field is anisotropic with chiral symmetry, where the handedness results from the orbital motion of the bound 3He pairs about an axis . This chiral superfluid, called the A phase or axial state, is stable at high pressure near the normal-to-superfluid transition, Fig. 1a–c, whereas the majority of the phase diagram is the non-chiral B phase, with isotropic physical properties. The stability of the A phase is attributed to strong-coupling effects arising from collisions between 3He quasiparticles10. However, in the presence of isotropic disorder these strong-coupling effects are reduced and the stable chiral phase disappears11,12, Fig. 1a. Here we show that anisotropic disorder can reverse this process and stabilize an anisotropic phase over the entire phase diagram, Fig. 1c.

Figure 1: Superfluid phase diagrams.
figure 1

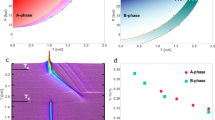
a–c, Comparison of pressure–temperature (P–T) phase diagrams of 3He in silica aerogels with various types of anisotropy in the limit H→0. High spatial uniformity of the aerogels, better than 99.97%, was established using optical cross-polarization methods16 for a and c. The solid black curves are fits to Tca(P) using the GL-scattering theory (Supplementary Information) and the solid (dashed) red curves correspond to the superfluid transition Tc (B → A transition TBA) for pure 3He at H=0. For subscripts, the lowercase a signifies aerogel and uppercase A and B represent the corresponding phases of superfluid 3He. a, A uniformly isotropic 98.2% porosity aerogel12. b, A 98.0% porosity aerogel axially compressed by 10% from torsional oscillator experiments25. In both a and b the B phase occupies the majority of the P–T plane. c, For the 97.5% porosity stretched aerogel used in the present work the A phase is stable throughout the phase diagram. The open squares (Td) mark the transition to a disordered chiral phase and the open circle at T=0 indicates a quantum critical point at which the superfluid order parameter vanishes (Fig. 2b). d, Left: Photograph of an aerogel with ∼98% porosity, 1 cm in diameter, partially extracted from the glass tube in which it was grown. Centre: Perspective view of the microstructure of the aerogel based on numerical simulation of diffusion-limited aggregation of silica particles, with diameter δ, into a network of strands with most probable spacing ξa. Right: The enlarged sketch shows the favourable directions (red arrows) of the chiral axes, , perpendicular to the strand.

Full size image

For many years it was thought to be impossible to introduce disorder into liquid 3He because it is intrinsically chemically and isotopically pure at low temperatures. Then it was discovered13,14 that 3He imbibed in ∼98% porosity silica aerogel, Fig. 1d, is a superfluid with a transition temperature that is sharply defined12, but reduced from that of pure 3He. To test predictions that isotropic disorder favours isotropic states and anisotropic disorder favours anisotropic states15, we have grown a 97.5% porosity anisotropic aerogel with growth-induced radial compression16, effectively stretching it along its cylinder axis by 14.3%. Experiments using uncharacterized stretched aerogels have been previously reported17,18 and are in disagreement with the work presented here. Silica aerogels, as in Fig. 1d, are formed by silica particles ≈3 nm in diameter, precipitated from a tetramethylorthosilicate solution, and aggregated in a diffusion-limited process. After supercritical drying we obtain a cylinder as shown in Fig. 1d. Our numerical simulation of this process indicates that the gel particles form strands (Fig. 1d). According to theory19, is constrained to point outward from the strand. Stretching an aerogel tends to align the strands, thereby forcing the chiral axis, on average, to be in an easy plane perpendicular to the aerogel anisotropy axis6. On the other hand, for an axially compressed aerogel should be aligned with the compression axis6.

We use pulsed nuclear magnetic resonance (NMR; Methods), to identify the 3He superfluid state and determine the magnitude of its order parameter, Δ. The equilibrium nuclear magnetization is tipped by a pulsed magnetic field to an angle β away from the static applied magnetic field, H, and the Fourier transform of its free precession is the NMR spectrum. The frequency shift of the spectrum, Δω, from the normal-state value centred at the Larmor frequency, ωL, is a direct measure of the temperature-dependent order parameter, Δ(T). For the A and B phases of 3He (ref. 10) the frequency shifts are

where ΩA,B2 is the square of the longitudinal resonance frequency, which is proportional to ΔA,B2 and determined by constants of the normal fluid: gyromagnetic ratio, γ; dimensionless dipole coupling constant, λD; and single-spin density of states at the Fermi level, NF; as well as the magnetic susceptibilities χA and χB. The A-phase susceptibility is temperature independent and equal to the normal-state value, χN; however, χB is temperature dependent and suppressed relative to χN.

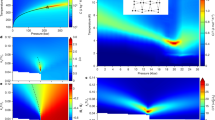
For 3He in our anisotropic aerogel we observe a sharp transition to a superfluid state at a temperature, Tca, marked by the onset of NMR frequency shifts for small tip angle, β=8° (Fig. 2a). Our comparison of the data with either of the two pure 3He states based on equations (1) and (2) indicates that the superfluid is an axial p-wave state similarly to the A phase. In the Ginzburg–Landau (GL) limit, T≲Tc, the initial slope of ΔωA is proportional to the square of the order parameter magnitude ΔA02, where ΔA2=ΔA02(1−T/Tc). We find in our anisotropic aerogel that ΔA02 has a linear pressure dependence, as shown in Fig. 2b, just as is the case for pure 3He-A (refs 20, 21). It is, however, substantially reduced in magnitude and extrapolates to a critical pressure of Pc=7.9 bar at T=0, where the order parameter vanishes at a quantum critical point22. We have analysed the transition temperatures Tca(P) using GL theory23 (Supplementary Information) to determine the mean free path λ=113 nm and the silica particle correlation length ξa=39 nm. Our calculated phase diagram compares very well with the data in Fig. 1c. With the same parameters we have also calculated ΔA02 (Supplementary Information), shown in Fig. 2b, and find excellent agreement with the order parameter determined from the frequency shifts, equation (1), consistent with a suppressed A phase. Moreover, extrapolation of Δω(P)→0 is at a pressure that coincides with the critical pressure from the calculated phase diagram, demonstrating important consistency between experiment and theory.

Figure 2: Identification of the superfluid state.
figure 2

a, The frequency shift of the NMR spectrum for a small tip angle, β=8°, as determined from Gaussian fits. The superfluid transition temperature at different pressures is marked by the onset of positive frequency shifts. The NMR spectra have been corrected for fast exchange of liquid spins with several layers of paramagnetic solid 3He on the aerogel surface14,28. b, The square of the order-parameter magnitude as a function of pressure in our aerogel (closed green circles) was calculated from the initial slopes in a using equation (1), showing the suppression relative to pure 3He-A (open and closed squares; refs 20, 21). The experimental results are compared with the predictions of the GL theory (open blue circles; Supplementary Information). The critical pressure, Pc=7.9 bar, is determined from an extrapolation (dashed line) of ΔA02 to zero, indicated by the arrow. The solid line is a linear fit to the pure A-phase data. c, Identification of the superfluid as the axial p-wave state follows from the agreement with theory24 (dashed blue curve) for the dependence of frequency shift Δω on tip angle, Td<T<Tc. d, The susceptibility for stretched and isotropic aerogel samples taken on warming at a pressure P≃26 bar in H=196 mT after subtraction of a paramagnetic background from solid 3He (ref. 14). For the isotropic aerogel the field-induced A-phase region has a constant susceptibility below Tca and a very sharp jump at the BA transition12. A similar jump in susceptibility would be anticipated for the stretched aerogel if the 3He were in the B phase or any other non-ESP phase.

Full size image

The tip-angle dependence of the NMR frequency shift is a fingerprint of a specific p-wave state10. Our measurements of Δω(β), Fig. 2c, follow the expected behaviour of the chiral axial state24, equation (1). The magnitude of the shift is reduced when compared with that of pure 3He-A, as shown in Fig. 2b. Furthermore, the axial state belongs to the class of equal-spin-pairing (ESP) states, with the same susceptibility as the normal Fermi liquid. We have directly demonstrated that this is the case as shown in Fig. 2d.

Last, we have looked for a possible phase transition to some other p-wave state by cooling to our lowest temperatures, ≲650 μK, in a substantial magnetic field of 196 mT, and measuring χ and Δω on warming. For example, if there had been a transition to a B phase on cooling we would have observed a discontinuous increase of χ on warming from the B phase to a magnetic field-induced A phase, as is characteristic of the first-order B-to-A transition in an isotropic aerogel (Fig. 2d; refs 12). Correspondingly, we would also have observed a discontinuous change in Δω. The absence of these discontinuities demonstrates that an ESP superfluid state in a stretched aerogel is stable down to our lowest temperatures.

Our three independent NMR measurements show that an anisotropic stretched aerogel stabilizes anisotropic superfluidity throughout the phase diagram, Fig. 1c. This is in stark contrast to 3He in the presence of isotropic disorder11,12, Fig. 1a, or for anisotropic disorder established by axial compression, Fig. 1b (ref. 25). In both of these latter cases the B phase is dominant. Understanding the stability of chiral superfluidity, stabilized by anisotropy, is an interesting open problem, in part because topologically non-trivial pairing states have unusual structure.

Our NMR results reported in Fig. 2a–c were restricted to temperatures within ∼20% of Tca. In this high-temperature region there is negligible increase in the NMR linewidth as compared with the normal fluid (Fig. 3), indicating that the chiral axis, , has a well-defined direction orthogonal to both the aerogel anisotropy axis6 and the magnetic field. This orientation minimizes the magnetic dipole energy, producing the so-called dipole-locked condition, on which the validity of equation (1) depends10, and with which our tip-angle results agree. The combined effects of the dipole energy and aerogel anisotropy define a uniform direction of for the A phase of superfluid 3He in our stretched aerogel.

Figure 3: The disorder transition.
figure 3

Below the disorder transition, T<Td (vertical dashed lines), the NMR frequency shift drops and the linewidth abruptly increases. The frequency shift is defined as the first moment of the NMR spectrum and the linewidth is the full-width at half-maximum. Both quantities have been corrected for the effect of fast exchange between liquid and surface solid 3He spins14,28. Data were taken on warming.

Full size image

At lower temperatures, we have discovered a different phase characterized by a significantly broadened NMR line. The data indicate that this superfluid state is no longer the homogeneous A phase with . On warming there is an abrupt increase in the first moment of the NMR spectrum (frequency shift) and a corresponding decrease in the linewidth at a well-defined temperature, Td (Fig. 3). The transition at Tdis independent of magnetic field for 31.1<H<196 mT. In addition, the magnetic susceptibility does not change at this temperature; however, Td is pressure dependent, as shown by the open squares in the phase diagram of Fig. 1c. We interpret these results as evidence for a disordered ESP phase with a possible phase transition at Td.

The frequency shift is a measure of ΔA, given in equation (1) for the dipole-locked case where the angle between the chiral axis and the magnetic field is . However, in general the shift also depends on θ, where for small tip angles Δω(θ) reduces to26

This enables us to extract the angular distribution, P(θ), of relative to H, from the NMR spectra both above and below Td. The observed spectrum is given by the convolution product of the normal-state lineshape and the frequency distribution P(ω) that corresponds to P(θ) determined by equation (3) (Supplementary Information). Above Td the NMR spectrum (Fig. 4a) can be fitted with an  distribution (Fig. 4b) that has a single component centred at θ=90°, as sketched in Fig. 4c, with angular spread Δθ=17.8°±3.6°. Examination of the spectrum below Td, Fig. 4a, indicates that it is bimodal, suggesting that P(θ) has three main components, which we take to be Gaussian functions with adjustable position, width and relative weight. From our fits we determine these parameters and obtain P(θ), Fig. 4b. For the spectra below Td, the disordered state is composed of three domains. Approximately one-third of the sample remains with whereas the majority, ∼2/3 of the distribution, has nearly zero frequency shift with θ=43.8°±0.1°. The theory, equation (3), does not distinguish between angles that are symmetric about θ=90°, and thus we assume that P(θ)=P(180°−θ) as shown in Fig. 4d. Our interpretation of the disordered state in terms of distinct  domains is different from the two-dimensional ‘orbital glass’ phase defined by a random distribution of confined to a plane perpendicular to the stretching axis6. It is noteworthy that the possible existence of orbital domains, such as we observe here, has been central to the discussion of time-reversal symmetry breaking in the unconventional superconducting state in Sr2RuO4 (ref. 27).

Figure 4: Distribution of the direction of the chiral axis.
figure 4

a, The convolution product of the normal-state NMR line (red curve) with a best-fit angular distribution of the chiral axis, P(θ), gives an excellent representation (dashed black curves) of the NMR spectra for the superfluid state above (left panel, bold green curve) and below (right panel, bold green curve) the disorder transition (Supplementary Information). The spectra were obtained with H=31.1 mT. b, The angular distributions for the chiral axis, , determined from a. The dashed pink curve is the distribution for Td<T<Tca. c, Stretching the aerogel along the cylinder axis forces into an easy plane perpendicular to the direction of strain6. To minimize the dipole energy must be perpendicular to H, as illustrated. d, According to our analysis the distribution splits into three  domains for T<Td.

Full size image

Methods

In our experiments the external magnetic field H was 31.1, 95.5 or 196 mT and oriented perpendicular to the aerogel cylinder axis. The sample was 4.93 mm long and had a diameter of 3.43 mm. The susceptibility was obtained by numerically integrating the phase-corrected absorption spectrum, whereas the frequency shift and linewidth were determined from the power spectrum. The sample was cooled using adiabatic nuclear demagnetization of PrNi5. NMR on 195Pt was used for thermometry at H=95.5 and 196 mT and calibrated relative to the known phase diagram of pure superfluid 3He from a volume of liquid outside the aerogel sample equal to 30% of the total liquid. For data acquired at H=31.1 mT, temperature was determined from the Curie–Weiss dependence of the solid 3He adsorbed to the aerogel surface14,28.