Abstract
The manipulation of matter waves had an important role in the history of quantum mechanics. The first experimental validation of matter-wave behaviour was the observation of diffraction of matter by crystals1, followed by interference experiments with electrons, neutrons, atoms and molecules using gratings and Young’s double slit2,3,4,5. More recently, matter-wave manipulation has become a building block for quantum devices such as quantum sensors6 and it has an essential role in a number of proposals for implementing quantum computers7,8. Here, we demonstrate the coherent control of the spatial extent of an atomic wavefunction by reversibly stretching and shrinking the wavefunction over a distance of more than one millimetre. The quantum-coherent process is fully deterministic, reversible and in quantitative agreement with an analytical model. The simplicity of its experimental implementation could ease applications in the field of quantum transport and quantum processing.
Similar content being viewed by others
Main
Cold atomic gases trapped in optical lattices (large and periodic ensembles of optical microtraps created by interfering optical laser beams) provide ideal tools for studying quantum transport in different regimes9,10 and quantum many-body systems in periodic potentials11,12,13,14,15. One of the challenges in this field is to coherently transfer matter waves between macroscopically separated sites. This would provide a mechanism to couple distant quantum bits and ultimately would lead to scalable quantum-information processing with cold atoms in optical lattices16. Recently, it was demonstrated that spatially driven lattice potentials in the presence of a linear potential can induce a coherent delocalization of a matter wave 17 when the driving is applied at the Bloch frequency νB, that is, the linear potential between adjacent sites expressed in frequency units. The delocalization occurs at integer multiples of νB because of the resonant coupling between Wannier–Stark levels within the same band. The resonances are characterized by a sinc2(π tΔν) spectral profile, where t is the driving time and Δν is the detuning of the driving from the resonant frequency. The sinc response here arises from the influence on the tunnelling current of the relative phase φ between the driving and the site-to-site quantum phase in the broadened wavefunction. When φ lies between 0 and π the wavefunction expands, whereas when it lies between π and 2π the wavefunction shrinks. In particular, when φ=2π the wavefunction returns to the starting point. Such a reversible behaviour is expected provided that the evolution of the wavefunction is fully coherent.
Any mechanism introducing loss of coherence would in fact lead to a non-reversible broadening. However, in a decoherence-free regime, it should be possible to engineer the spatial extension of the wavefunction using the frequency offset and the amplitude of the driving as tuning knobs. Here, we experimentally demonstrate this new technique of matter-wave manipulation by showing that coherent delocalization results in an extended distribution corresponding to the size of the broadened wavefunction. This is demonstrated by observing in situ the breathing of the wavefunction under non-resonant driving conditions, and through a self-interference technique based on time-of-flight (TOF) expansion. Our experimental findings are supported by a theoretical model with which we can determine analytically the spatial wavefunction under the action of the driving18,19.
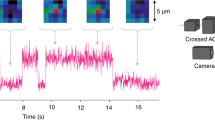
To drive (that is, modulate) the phase of the lattice potential, we apply a sinusoidal voltage (with frequency νPZT) to the piezoelectric transducer (PZT) that supports the retro-reflecting mirror of the standing-wave dipole trap (Fig. 1). In a first set of measurements, we test the spatial coherence of the broadened wavefunction by observing the periodic breathing of the atomic distribution while we drive the PZT with a non-zero frequency detuning Δν=νPZT−νB. Figure 1 shows the image of the atomic distribution under hard driving conditions. The frequency detuning Δν is set to about 0.26 Hz such that the revival period, equal to Δν−1, is about 4 s and the amplitude of the driving is set to its maximally experimentally accessible value, 10 lattice sites peak-to-peak. The spatial profile is initially Gaussian, corresponding to the initial spatial distribution of the atoms in the magneto-optical trap. The profile then evolves into a more complex shape as a result of the wavefunction broadening 18,19, but then at the revival the distribution returns to its initial profile. Starting from a size of 31 μm, it reaches an extension larger than 1.5 mm, and then it returns to a size of 40 μm. In other words, the distribution increases its size by a factor larger than 20 and then returns to almost its initial value. The observation of the exact refocusing to the original size is hampered by technical limitations (see Fig. 1). Intermediate values of the spatial extent can be obtained in a reproducible and reversible way by varying the amplitude or frequency detuning Δν of the driving voltage.
Left: cold strontium atoms are trapped in an optical lattice potential aligned along the Earth’s gravity field g. The standing wave originating the lattice potential is axially driven by applying a sinusoidal voltage to the PZT holding the retro-reflecting mirror. The diagram is not to scale. Right: spatial distribution of the atoms for various durations T of a non-resonant driving (0 to 3.8 s from left to right). The colour scale is adapted to each picture so that the visibility is maintained with the varying atomic densities. With the maximum modulation and a frequency detuning Δν set to about 260 mHz, the transport extends on the millimetre scale and shows a revival time of 3.8 s. At T=0 the in situ r.m.s. spatial width is 31 μm, whereas at T=3.8 s it becomes 40 μm.
In Fig. 2, we show the time evolution of the spatial extent for different values of frequency detuning Δν. With Δν equal to +5 and −5 Hz, the breathing shows a revival with the expected period of 5 Hz, and a constant visibility on a 1 s timescale, regardless of the sign of the frequency detuning. With Δν=0.5 Hz, again the atomic distribution shows a breathing at a frequency equal to Δν, and from the reduction of the oscillation amplitude over time we can infer a e−1 damping time of 28 s. The results presented in Figs 1 and 2 cannot be explained classically and show a quantitative agreement with the analytic expression of the wavefunction expected for the driven potential18,19. This implies that we manipulate and directly observe the spatial wavefunction on a length scale larger than 1 mm.
For short times, the minimum size corresponds to the size of the non-driven atomic cloud. a–c, Detuning Δν=νPZT−νB=+5 Hz (a), Δν=−5 Hz (b) and Δν=−0.5 Hz (c). The driving amplitude is set to about 1 (a,b) and 0.2 (c) lattice sites peak-to- peak. The reported spatial extent is defined as the r.m.s. radius calculated on the atomic distribution. Each data point is the average of five measurements and the error bars show the standard deviation of the average calculated on the corresponding data set. The damping observed on the periodic dynamics is attributed mostly to the off-resonant scattering of the trapping photons. From the data in c, we infer a 1/e− damping time of about 28 s. In each graph, the fitted line gives a periodicity consistent with Δν−1.
To study the coherence properties of the modified wavefunction, we measure the interference of the wavefunction with itself. To this end, the wavefunction is expanded in TOF after an adiabatic release from the lattice potential. We record the evolution for an expansion varying between 0 and 25 ms under various driving conditions. First, we consider the case of resonant driving (Δν=0). An integer number of sinusoidal cycles, up to 120 (equivalent to 210 ms when νB=574.14 Hz), is applied to the PZT such that the wavefunction broadens proportionally with time. The atomic distribution is then probed in TOF 300 ms after the beginning of the driving, and after switching off the lattice potential adiabatically on a 20 μs timescale. Figure 3 shows the changes in the expansion after 15 ms of TOF for various broadening conditions. In the absence of a driving, the sample expands as expected yielding a Gaussian profile. When we drive the system, we clearly observe the appearance on a transient time of a non-Gaussian distribution characterized by a narrow peak emerging from the broader pedestal. This transient effect results from the interference among the probability amplitudes originating from the different portions of the wavefunction and it is confirmed by a simulation of the ballistic expansion of the broadened wavefunction (see the Methods section).
The TOF is fixed to 15 ms and a resonant driving is applied for the amount of cycles reported on each row. Left: two-dimensional density profile. In the pictures, the gravity and the lattice are horizontally oriented. Right: the atomic density integrated along the transverse direction of the lattice. The red line is the distribution expected from the ballistic expansion of the analytical expression of the broadened wavefunction (see the Methods section). We maintain the same colour scale on the two-dimensional distributions and the vertical scale on the integrated density profiles for the five cases. The appearance of the narrow peak in the ballistic expansion results from a transient interference effect to which contributes the entire population of the sample.
We verified that the narrow peak in TOF does not arise from a trivial selection of a given momentum class nor a temperature reduction for a fraction of the population. In fact, for the conditions of Fig. 3, the overall number of atoms does not change with the number of applied cycles, whereas the atomic distribution gathers in the central peak as a phenomenon of interference alone. As an extra check, we verified that for longer TOF the same Gaussian distribution in the momentum space is observed both with and without driving. For a fixed duration of the TOF, the narrow peak reaches maximum visibility compared with the pedestal when the size of the broadened wavefunction is a fraction of the size of the non-driven and ballistically expanded sample.
In addition, for a static lattice (that is, without a driving applied to the PZT), the position of the interference peak depends on the time spent in the lattice potential exhibiting a periodic dynamics at the Bloch frequency νB. This result, shown in Fig. 4, reflects the time evolution of the site-to-site phase differences in the broadened wavefunction that is induced by the gravity potential. This dynamics is confirmed by numerical simulations of the expansion of the wavefunction. In the absence of driving, on the other hand, the shape of the distribution after ballistic expansion shows neither an interference peak nor a periodic signal. Originated from the dynamics of the wavefunction’s phase gradient, this phenomenon is in analogy with Bloch oscillations that occur in the momentum space for atoms at sub-recoil temperatures20. On the other hand, the periodic dynamics of the interference peak happens regardless of the initial temperature of the sample. This may find applications in the realization of precise force sensors using species difficult to cool to sub-recoil temperatures.
First, the atomic wavefunction is stretched to a fixed size. Then the atoms are kept in the static lattice potential for a varying time, and finally they are probed after a fixed ballistic expansion. The combined effect of the static lattice potential and the Earth’s gravity field induces a linear increase of the site-to-site phase in the broadened wavefunction, which is directly observable in the ballistic expansion as a periodic evolution of the interference peak keeping a fixed TOF duration of 15 ms. From top to bottom, the hold time in the static lattice increases linearly over one Bloch period (about 1.75 ms).
The pictures in Fig. 3 and the related analysis are made by starting the TOF at the point where the site-to-site phase difference is zero or, equivalently, the emerging narrow peak is centred on the pedestal.
The dynamics that we observe, both in situ and in TOF, can be described starting from the expression of the broadened wavefunction18,19

of the initial state |n〉, where |m〉 are the Wannier–Stark eigenstates of the static Hamiltonian (with the gravity potential and the non-modulated lattice) labelled by the index m of their position expressed in lattice units, t is the time of driving, Ω is a coefficient accounting for the tunnelling rate among the lattice barriers and Jn are the Bessel functions of the first kind. The assumption that the initial state corresponds to the Wannier–Stark eigenstate |n〉 is consistent with the fact that the trapped atoms are derived from a thermal sample at a temperature higher than the recoil temperature and they uniformly fill the first band. The thermal de Broglie wavelength is shorter than the lattice period, so when we load the atoms into the lattice potential the coherence degree among adjacent Wannier–Stark eigenstates is negligible.
In addition, we verified that the wavefunction also exhibits revivals in the interference pattern for the TOF distribution under non-resonant driving. In Fig. 5, we compare the TOF profiles taken for different expansion times under three different conditions: without driving, at maximum expansion and at the spatial revival, while the frequency detuning Δν is set to about 2 Hz. The TOF expansion at maximum broadening is equivalent to that obtained under resonant driving except that now the distribution is deliberately asymmetric because of a different choice of the site-to-site phase difference at the release (same as in Fig. 4, case 5). On the other hand, the TOF expansion at the revival is the same as that in the absence of driving.
The reversible dynamics of the spatial extent have their counterpart in the ballistic expansion signal. From left to right: in situ distribution, 10 ms and 15 ms TOF. a, No driving. b, Maximum expansion. c, First spatial revival. In b, the driving conditions are the same as those in Fig. 3 for 80 cycles, except that here we use a 2.28 Hz frequency detuning of the driving field with respect to the Bloch frequency. In c, the interference peak is absent, denoting, as expected, the revival of the wavefunction also in the momentum space. The displacement along the horizontal axis for different TOF times corresponds to the free fall in the Earth’s gravity field.
The control of transport discussed here proves in its simplicity that matter waves can be coherently manipulated over macroscopic distances in optical lattice potentials. The proposed method can be extended to control travelling waves19,21, with applications in guiding and splitting atomic wavefunctions. This suggests possible implementations of quantum gates exploiting controlled interactions with ultracold atoms16,22.
Methods
Experimental set-up and procedure.
The experimental set-up was described previously in ref. 23. About 106 88Sr atoms are laser cooled to a temperature of 1 μK and are subsequently loaded into a vertical lattice potential produced by the dipole force of a λL=532 nm laser field. The lattice is formed by retro-reflecting the laser light with a mirror mounted on top of a PZT. The phase of the optical lattice, defined to be zero at the surface of the mirror, is modulated by applying a time-dependent voltage to the PZT with a maximum excursion of 10 lattice sites peak-to-peak. The experimental set-up is supported on pneumatic suspensions to suppress seismic noise in the lattice reference. This, on the other hand, introduces small instabilities of the orientation of the set-up, which result in drifts on the definition of νB. These, in turn, are responsible for the difficulty to resolve the exact moment of refocusing of the distribution, especially at long interrogation times and fast tunnelling rate as reported in Fig. 1. The depth of the lattice potential is typically eight recoil energies ER (ER=h2/2m λL2=kB×381 nK) along the optical axis of the trapping beam and it decreases exponentially in the radial direction owing to the Gaussian spatial profile. As initially the atoms are hot with respect to the recoil temperature, when they are loaded into the lattice potential they occupy almost uniformly the first band and, with decreasing weight, the higher bands. Owing to Landau–Zener tunnelling, the atoms have a lifetime shorter than 100 ms in all of the bands except for the first one where the atoms live longer than our experimental timescale. We exploit this fact to select only the atoms that lie in the first band by initially waiting a time of 100 ms in the static potential before applying the driving. The atomic distribution is measured by absorption imaging of a resonant laser beam detected on a CCD (charge-coupled device) camera.
Calculation of the spatial distribution after ballistic expansion.
We calculated the spatial distribution after ballistic expansion of the broadened sample by applying the free-particle evolution operator to the wavefunction in equation (1). We chose the same conditions as in Fig. 3, where Δν=0 and the speed of broadening Ω=430 sites s−1. We numerically carried out the calculation by Fourier transforming |n(t)〉 in the momentum space where the free-particle Hamiltonian is diagonal. After 15 ms of TOF, we reconstructed the wavefunction in the real space. Finally, we applied a convolution with a Gaussian distribution 30 μm wide (r.m.s.) which accounts for the initial size of the atomic sample just after the loading into the lattice potential.
References
Davisson, C. & Germer, L. H. The scattering of electrons by a single crystal of nickel. Nature 119, 558–560 (1927).
Jönsson, C. Elektroneninterferenzen an mehreren künstlich hergestellten Feinspalten. Z. Phys. 161, 454–474 (1961).
Zeilinger, A., Gahler, R., Shull, C. G., Treimer, W. & Mampe, W. Single and double slit diffraction of neutrons. Rev. Mod. Phys. 60, 1067–1073 (1988).
Carnal, O. & Mlynek, J. Young’s double-slit experiment with atoms: A simple atom interferometer. Phys. Rev. Lett. 66, 2689–2692 (1991).
Arndt, M. et al. Wave-particle duality of C60 molecules. Nature 401, 680–682 (1999).
Peters, A., Chung, K. Y. & Chu, S. Measurement of gravitational acceleration by dropping atoms. Nature 400, 849–852 (1999).
Monroe, C., Meekhof, D., King, B. & Wineland, D. A ‘Schrödinger cat’ superposition state of an atom. Science 272, 1131–1136 (1996).
Monroe, C. Quantum information processing with atoms and photons. Nature 416, 238–246 (2002).
Madison, K. W., Fischer, M. C., Diener, R. B., Niu, Q. & Raizen, M. G. Dynamical Bloch band suppression in an optical lattice. Phys. Rev. Lett. 81, 5093–5096 (1998).
Browaeys, A., Haeffner, H., McKenzie, C., Rolston, S. L., Helmerson, K. & Phillips, W. D. Transport of atoms in a quantum conveyor belt. Phys. Rev. A. 72, 053605 (2005).
Cataliotti, F. S. et al. Josephson junction arrays with Bose–Einstein condensates. Science 293, 843–846 (2001).
Bloch, I. Ultracold quantum gases in optical lattices. Nature Phys. 1, 23–30 (2005).
Gemelke, N., Sarajlic, E., Bidel, Y., Hong, S. & Chu, S. Parametric amplification of matter waves in periodically translated optical lattices. Phys. Rev. Lett. 95, 170404 (2005).
Sias, C. et al. Resonantly enhanced tunnelling of Bose–Einstein condensates in periodic potentials. Phys. Rev. Lett. 98, 120403 (2007).
Sias, C. et al. Observation of photon-assisted tunneling in optical lattices. Phys. Rev. Lett. 100, 040404 (2008).
Bloch, I. Quantum coherence and entanglement with ultracold atoms in optical lattices. Nature 453, 1016–1022 (2008).
Ivanov, V. V. et al. Coherent delocalization of atomic wave packets in driven lattice potentials. Phys. Rev. Lett. 100, 043602 (2008).
Thommen, Q., Garreau, J. C. & Zehnlé, V. Quantum interference in a driven washboard potential. Am. J. Phys. 72, 1017–1025 (2004).
Thommen, Q., Garreau, J. C. & Zehnlé, V. Atomic motion in tilted optical lattices: An analytical approach. J. Opt. B 6, 301–308 (2004).
Dahan, M. B., Peik, E., Reichel, J., Castin, Y. & Salomon, C. Bloch oscillations of atoms in an optical potential. Phys. Rev. Lett. 76, 4508–4511 (1996).
Creffield, C. E. Quantum control and entanglement using periodic driving fields. Phys. Rev. Lett. 99, 110501 (2007).
Ye, J., Kimble, H. J. & Katori, H. Quantum state engineering and precision metrology using state-insensitive light traps. Science 320, 1734–1738 (2008).
Ferrari, G., Poli, N., Sorrentino, F. & Tino, G. M. Long-lived Bloch oscillations with bosonic Sr atoms and application to gravity measurement at the micrometre scale. Phys. Rev. Lett. 97, 060402 (2006).
Acknowledgements
We would like to thank M. Artoni, N. Poli, C. W. Oates and M. L. Chiofalo for stimulating discussions, M. Schioppo for his contribution in the early stage of the experiment and R. Ballerini, M. De Pas, M. Giuntini, A. Hajeb and A. Montori for technical assistance. This work was supported by LENS, INFN, EU (under Contract No. RII3-CT-2003 506350 and the FINAQS project), ASI and Ente CRF.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Alberti, A., Ivanov, V., Tino, G. et al. Engineering the quantum transport of atomic wavefunctions over macroscopic distances. Nature Phys 5, 547–550 (2009). https://doi.org/10.1038/nphys1310
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys1310
This article is cited by
-
Visual observation of photonic Floquet–Bloch oscillations
Light: Science & Applications (2024)
-
Observation of Bloch oscillations and Wannier-Stark localization on a superconducting quantum processor
npj Quantum Information (2021)
-
From super-Bloch oscillations to sudden self-trapping in Bose–Einstein condensates with inter-atomic interactions
Nonlinear Dynamics (2020)
-
Ground states of a Bose-Einstein Condensate in a one-dimensional laser-assisted optical lattice
Scientific Reports (2016)
-
Parametric excitation and squeezing in a many-body spinor condensate
Nature Communications (2016)