Abstract
The detailed nature of fluid flow over a cylinder is one of the fundamental topics in classical fluid dynamics as it demonstrates flow separation and vortex shedding1. In superfluid helium, either He (II) or the B phase of3He, an important question has been to what extent these quantum fluids show classical fluid turbulent states2,3,4. Although the existence of turbulent structures can be inferred using precise instrumentation5,6, direct visualization of the flow field can provide unequivocal evidence of these phenomena. Here we show the existence of large turbulent structures in He (II) counterflow across a cylinder as obtained by the particle image velocimetry technique. Compared with classical fluid flow, the particle motion driven by He (II) counterflow shows macroscopic eddies downstream of the cylinder but also similar structures are observed in front of the cylinder, behaviour not seen in classical fluids. As Landau’s two-fluid model7 for He (II) describes counterflow as the relative motion of the superfluid and normal fluid components, the current results indicate that both components may be undergoing a kind of flow separation as they pass over the cylinder.
Similar content being viewed by others
Main
Visualizing the flow of superfluid4He (He(II)) has long been of interest to the scientific community8,9,10,11. Particle image velocimetry (PIV), a quantitative visualization technique that records the motion of micrometre-scale solid particles suspended in the fluid and uses that information to map out the flow field of a dynamic fluid12, has been used extensively in classical fluids, but only applied in the past few years to the study of liquid helium fluid dynamics13,14. This delay has at least in part been because of the challenges of particle selection and seeding into a fluid of very low temperature and low density. The entire process must occur in an optical He(II) cryostat with the visualization equipment consisting of a charge-coupled-device camera, a dual-head pulse laser, beam-expanding optics, a synchronizer for timing and triggering and a data-acquisition computer. To map the velocity field, sequential images of the suspended particles are collected and divided with a grid into a large number of ‘interrogation regions’, each of which provides a local velocity vector based on averaging the particle velocities in that region. The interrogation regions typically contain ten particles and are about 1×1 mm2, which establishes the approximate spatial resolution of the measurement.
In the two-fluid model for He(II), the viscous normal fluid component density, ρn, increases with temperature T and the corresponding inviscid superfluid component density, ρs, decreases with T until it vanishes at the transition to He(I), just below 2.2 K. A heat current q produces a normal fluid velocity, vn, which is given by the relationship7

where ρ is the total density and s is the fluid entropy. In this case, the superfluid component velocity, vs, is in the opposite sense conserving the zero net momentum condition such that

This internal convection of the two fluid components is known as thermal counterflow.
As the PIV technique maps out the velocity field of particles suspended in the fluid, it is not a trivial problem to relate the observed particle motion to the individual velocity fields of the normal and the superfluid components in He(II). Our experiments on counterflow in a one-dimensional channel have shown that, in a similar manner to classical fluids, the particle motion is approximately uniform and parallel15. However, quantitative analysis of these data has indicated that the interaction between the suspended particles and the two fluid components is more complex than one might assume, with the turbulent superfluid component also exerting a force on the particles. This observation is further supported by theoretical studies that have suggested the particle–superfluid interaction may be associated with pinning of the quantized vortex lines in the turbulent superfluid component16,17.
In the present experiment, we have used the PIV technique to visualize counterflow He(II) over a circular cylinder. Counterflow is produced in a one-dimensional rectangular channel that is 200 mm long and has a cross-section of 38.9×19.5 mm2. The channel is immersed in a constant-temperature He(II) bath and seeded with 1.7-μm-diameter polymer particles (specific gravity=1.1)14. The top end of the channel is open to the helium bath whereas the lower end is closed and contains a nichrome thin-film heater. On each side wall of the channel there is an optical window for the laser sheet in and out. The front wall has a 45×20 mm2 optical window that transmits the images to the charge-coupled-device camera. A 6.35-mm-diameter transparent cylinder is located inside the channel spanning the full width and orthogonal to the fluid flow. In the widest part of the cylinder, the channel cross-section is therefore reduced to 68% of its original area.
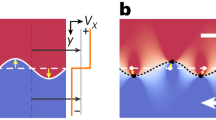
An example of the raw data produced by these PIV experiments is shown in Fig. 1, which is an image of the suspended particles in the He(II) channel. See Supplementary Information to view a video of the particle motion at 2.03 K produced by an 11.2 kW m−2 steady heat current from below the cylinder. This flux corresponds to a vortex line density L0 of about 2.6×1010 m m−3 and an average line spacing of about 6.2 μm; ref. 18. In the video, one can easily resolve large convective cells behind the cylinder at the approximate angles of 45 and 135∘. These cells are roughly of the same diameter as the cylinder and seem to maintain stable locations over the 10 s duration of the video. In addition, convective cells are also seen in front of the cylinder, at about 225 and 315∘. These cells are of similar size but seem to be slightly closer to the channel walls. For comparison, in classical flow over a cylinder the streamlines in front of the cylinder are smooth and large vortices are only observed behind the cylinder. Thus, these vortices in front of the cylinder have no classical analogue.
It should be pointed out that large-scale vortex rings in He(II) were reported while measuring the velocity profile in a He(II) counterflow jet using the laser Doppler velocimetry technique10,11. However, it is believed that the large vortex structures were probably caused by an experimental artefact that resulted in cavitation in the counterflow jet rather than, as in our experiments, the complex interaction between the two fluid components.
Two examples of the computed velocity vectors for counterflow across a cylinder obtained from the analysed PIV data are shown in Fig. 2. The coloured contour represents the particle velocity magnitude with the velocity scale indicated at the top of each figure and in the figure caption. Velocity streamlines for the same two cases are shown in Fig. 3. Comparing these two figures, one can clearly see a higher level of turbulence for Fig. 3b than for Fig. 3a.
By analogy to classical fluids, one might expect the scale of the turbulence to increase with Reynolds number, in this case defined in terms of the normal fluid velocity and viscosity, μn, as

where D is the diameter of the cylinder. Note that equation (1) uses the total density rather than the normal fluid density, a form normally used to correlate frictional pressure drop in He(II) flow in tubes19 and over bluff bodies20. However, computing the Reynolds number for the two cases in Figs 2 and 3 gives ReD∼41,000 for Fig. 2a and ReD∼21,000 for Fig. 2b, which is a value lower by about a factor of two even though it shows more turbulence than Fig. 2a. This suggests that the Reynolds number as defined in equation (1) may not be the appropriate parameter to describe the scale of the turbulence in counterflow He(II). In other experiments not shown here, we have attempted to match the Reynolds numbers at different temperatures and heat currents; however, in all cases, the level of turbulence is greater at higher temperatures.
Furthermore, it is worth noting that for classical fluids at ReD>10,000 considerably different flow structures are normally present downstream of a cylinder. In particular, the large-scale vortices behind the cylinder show vortex shedding, where the structures are generated periodically and detach from the cylinder producing a dynamic wake. Such time-dependent phenomena in classical fluids result in pressure fluctuations that are not present in He(II) counterflow in wide channels. In fact, the vortex structures present in these counterflow He(II) experiments show behaviour that is qualitatively similar to the steady wakes seen in classical flow over a cylinder at low Reynolds number, ReD<50 (ref. 21).
Finally, as can be seen in Fig. 3, the location of the large vortices in front of the cylinder seems closer to the channel wall than do those downstream of the cylinder. This asymmetry of particle motion may be further evidence that the normal fluid component interacts more strongly with the particles than does the turbulent superfluid component. As the particle motion in front of the cylinder should be determined by both the counterflowing superfluid component and the normal fluid component, which has a significant horizontal velocity component, one would expect the normal fluid to move the vortex in front of the cylinder farther away from it. Apart from these qualitative observations of particle motion during counterflow around a cylinder and its explanation in terms of interactions with both the superfluid and normal fluid component, we have no theoretical justification for these results at present. This is an area of current research.
It remains to be seen how the present results can help us understand the flow of heat currents in counterflow He(II) around bluff bodies. This topic is of significant interest to scientists and engineers who use He(II) to cool large technical devices such as superconducting magnets and particle physics accelerators. The design of such devices is frequently based on extensions of the two-fluid model and its application in complex geometries. By visualizing counterflow around a cylinder, we show that the corresponding heat current may have more complex behaviour than one might assume.
References
Schlichting, H. Boundary Layer Theory 7th edn Ch. 2 (McGraw Hill, New York, 1979).
Stalp, S. R., Skrbek, L. & Donnelly, R. J. Decay of grid turbulence in a finite channel. Phys. Rev. Lett. 82, 4831–4834 (1999).
Vinen, W. F. Classical character of turbulence in a quantum fluid. Phys. Rev. B 61, 1410–1420 (2000).
Vinen, W. F. & Niemela, J. J. Quantum turbulence. J. Low Temp. Phys. 128, 167–231 (2002).
Finne, A. P. et al. An intrinsic velocity-independent criterion for superfluid turbulence. Nature 424, 1022–1025 (2003).
Bradley, D. I. et al. Emission of discrete vortex rings by a vibrating grid in superfluid3He – B: precursor to quantum turbulence. Phys. Rev. Lett. 95, 035302 (2005).
Landau, D. The theory of superfluidity of helium II. J. Phys. (USSR) 5, 71 (1941).
Chopra, K. L. & Brown, J. B. Suspension of particles in liquid helium. Phys. Rev. 108, 157 (1957).
Chung, D. Y. & Critchlow, P. R. Motion of suspended particles in turbulent superflow of liquid helium II. Phys. Rev. Lett. 14, 892–894 (1965).
Murakami, M., Nakai, H., Ichikawa, N., Hanada, M. & Yamazaki, T. in Proc. 11th Int. Cryog. Engn. Conf. (Berlin) 582–586 (Butterworth, Surrey, UK, 1986).
Murakami, M. & Ichikawa, N. Flow visualization of a thermal counterflow jet in He II. Cryogenics 29, 438–443 (1989).
Adrian, R. J. Particle–imaging techniques for experimental fluid mechanics. Annu. Rev. Fluid Mech. 23, 261–304 (1991).
Donnelly, R. J. et al. The use of particle image velocimetry in the study of turbulence in liquid helium. J. Low Temp. Phys. 126, 327–332 (2002).
Zhang, T., Celik, D. & Van Sciver, S. W. Tracer particles for application to PIV studies of liquid helium. J. Low Temp. Phys. 134, 985–1000 (2004).
Zhang, T. & Van Sciver, S. W. The motion of micron-size particles in He II counterflow as observed by the PIV technique. J. Low Temp. Phys. 138, 865–870 (2005).
Poole, D. R., Barenghi, C. F., Sergeev, Y. A. & Vinen, W. F. Particle dynamics in helium II. J. Low Temp. Phys. 138, 487–492 (2005).
Poole, D. R., Barenghi, C. F., Sergeev, Y. A. & Vinen, W. F. The motion of tracer particles in helium II. Phys. Rev. B 71, 064514 (2005).
Tough, J. T. Progress in Low Temperature Physics Vol. 6 Ch. 3, 147–155 (North Holland, Amsterdam, 1982).
Walstrom, P. L., Weisend, J. G. II, Maddocks, J. R. & Van Sciver, S. W. Turbulent flow pressure drop in various He II transfer system components. Cryogenics 28, 101–109 (1988).
Smith, M. R., Hilton, D. K. & Van Sciver, S. W. Observed drag crisis on a sphere in flowing He I and He II. Phys. Fluids 11, 1–3 (1999).
Williamson, C. H. K. Vortex dynamics in a cylindrical wake. Ann. Rev. Fluid Mech. 28, 477–539 (1996).
Acknowledgements
This work was supported in part by the National Science Foundation, Division of Chemical Transport Systems and by the Department of Energy, Division of High Energy Physics. The authors would like to thank L. Lourenco, S. Fuzier and S. Maier for assistance in performing these experiments.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
This file contains a video image of the particle motion around the cylinder at 2.03 K produced by an 11.2 kW/m2 steady heat current through the He II from below. This flux corresponds to a vortex line density of about 2.6 x 1010 m/m3 and an average line spacing of about 6.2 μm. The particles are 1.7 μm diameter polymer micro-spheres with a specific gravity of 1.1. (SWF 2665 kb)
Rights and permissions
About this article
Cite this article
Zhang, T., Van Sciver, S. Large-scale turbulent flow around a cylinder in counterflow superfluid4He (He (II)). Nature Phys 1, 36–38 (2005). https://doi.org/10.1038/nphys114
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys114
This article is cited by
-
Imaging quantized vortex rings in superfluid helium to evaluate quantum dissipation
Nature Communications (2023)
-
Observing flow of He II with unsupervised machine learning
Scientific Reports (2022)
-
Atomic-scale visualization of electronic fluid flow
Nature Materials (2021)
-
Molecular Tagging Velocimetry in Superfluid Helium-4: Progress, Issues, and Future Development
Journal of Low Temperature Physics (2019)
-
Statistical Measurement of Counterflow Turbulence in Superfluid Helium-4 Using \(\hbox {He}_2^*\) Tracer-Line Tracking Technique
Journal of Low Temperature Physics (2017)