Main

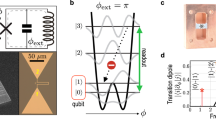
The system considered is shown schematically in the inset of Fig. 1a with a scanning electron micrograph provided in Fig. 1b. It consists of a three-junction flux qubit14 with the two qubit states corresponding to persistent currents of amplitude Ip flowing clockwise and anticlockwise. When operated in the vicinity of the degeneracy point, fx≡Φx/Φ0−1/2≈0, where Φx is the magnetic flux applied to the qubit loop and Φ0=h/2e is the flux quantum, the Hamiltonian of the qubit in the basis of the persistent current states reads

Here, σi are Pauli matrices, Δ is the tunnelling amplitude and ɛ(fx)=2Φ0Ipfx is the energy bias. The energy levels of the isolated qubit, separated by , are shown in Fig. 1. The qubit is driven by a high-frequency field with frequency ωd and coupled through a mutual inductance M to a low-frequency tank circuit with frequency much lower than the level spacing of the qubit, ℏωT≪Δ. Both the high-frequency driving and the coupling to the tank circuit can be included at this stage through their contributions to the external flux Φx. The slowly oscillating current in the tank circuit can be treated in an adiabatic approximation, that is, it shifts the bias flux of the qubit by Φx(t)=M[Id.c.+Ir.f.(t)]. To illustrate the principle, we first treat Ir.f.(t) as a classical a.c. current. For the quantitative description provided below, we will quantize this oscillator degree of freedom.

Figure 1: The system and the operation principles.
figure 1

a, The energy levels of the qubit as a function of its energy bias ɛ(fx)=2Φ0Ipfx. The sinusoidal current in the tank coil indicated by wavy lines, with its instantaneous value indicated by the dot, drives the bias of the qubit. The cooling and amplification cycles are marked by blue and red, respectively. The resonant excitation of the qubit due to the high-frequency driving, with amplitude ΩR0, is indicated by two green arrows and the Lorentzian depicting the width of this resonance. The frequency of this driving is kept constant, whereas the detuning is controlled by the d.c. bias of the qubit. The relaxation of the qubit is denoted by the black dashed arrows. The inset shows schematically the three-junction qubit coupled to the LC circuit. An onchip microwave antenna (not shown) couples the high-frequency driving to the qubits. b, Scanning electron micrograph of the superconducting flux qubit prepared by the shadow evaporation technique.

Full size image

The system mimics the Sisyphus mechanism of damping (cooling) and amplification (tendency towards lasing) known from quantum optics13. This mechanism is shown in Fig. 1. Here, we describe the damping (cooling, hence marked in blue) for a situation where the driving is red-detuned, ℏωd<ΔE; the amplification (marked in red) for blue-detuning can be described in an analogous way. The oscillations of the current in the tank circuit, Ir.f.(t), lead to oscillations of ɛ(fx) around a value determined by the d.c. component, Id.c.. In the first part of the cycle, when the qubit is in the ground state, the current shifts the qubit towards the resonance at ΔE=ℏωd. The energy of the qubit grows owing to the work done by the inductor–capacitor (LC) circuit. Once the system reaches the vicinity of the resonance point, the qubit can be excited, the energy being provided by the high-frequency driving field. With parameters adjusted such that this happens at the turning point of the oscillating trajectory, in the following the qubit in the excited state is shifted away from the resonance, such that the qubit’s energy continues to grow. Again the work has to be provided by the LC circuit. The cycle is completed by a relaxation process that takes the qubit back to the ground state, while the work carried out by the oscillator together with a quantum of energy of the high-frequency driving is released to the environment. The maximum effect is achieved when the driving frequency and relaxation rate are of the same size. If the relaxation is too slow, the state is merely shifted back and forth adiabatically during many periods of oscillations. Note that the complete cycle resembles the ideal Otto-engine thermodynamic cycle15. Although the cooling cycle described here differs in some details from the one in atomic systems13 where more than two levels are involved and the transition mechanism is different, it demonstrates the basic idea of Sisyphus cooling.

We have carried out two types of measurement. In the first, a response analysis, the LC tank circuit is driven near-resonantly by a low-frequency radiofrequency current, and its response is detected using lock-in techniques. In these measurements, we identify the influence of the high-frequency driven qubit on the effective quality factor and eigenfrequency of the tank circuit. We associate a reduction of the effective quality factor with cooling, whereas the enhancement of the effective quality factor is associated with amplification and tendency towards lasing. Our quantitative analysis enables us to identify parameter regimes where these effect are optimized.

In the second type of measurements, the low-frequency radiofrequency driving is switched off, while the emission of the LC tank circuit is monitored by a spectrum analyser. This analysis probes the influence of the qubit on the effective quality factor, and, most importantly, enables us to determine the energy stored in the tank circuit. Thus, we are able to demonstrate cooling and amplification of the LC oscillator. Note, that the increase of the number of photons in the LC circuit in the amplification regime is not simply heating, because it is accompanied by an increase of the effective quality factor and a linewidth narrowing. This property indicates a tendency towards lasing, although the system considered here does not yet reach the lasing instability.

Our results of the first type of experiment are shown in Fig. 2. The dips (peaks) correspond to the Sisyphus damping (amplification) of the tank circuit, that is, to the decrease (increase) of the effective quality factor Qtank. The central dip is due to the shift of the oscillator frequency when the qubit is at its degeneracy point16 and is not related to the Sisyphus effect. We observe from Fig. 2b that the extra voltage saturates for large driving amplitudes at approximately 200 nV. Using this value and equation (6) (see the Methods section), we observe that indeed the relaxation time is close to the period of oscillations, ΓR≈0.2ωT or ΓR≈0.8ωT (two solutions are allowed by equation (6)). We also note that the distance between the points of optimal damping and optimal amplification grows with the amplitude of the external low-frequency driving. This confirms our conjecture that the cooling (amplification) is optimized when the oscillating current, Ir.f.(t), brings the qubit into the resonance with the microwave driving at the turning point of oscillations of Ir.f.(t) (Fig. 1a).

Figure 2: Influence of high-frequency driving of the qubit on the low-frequency response of the tank circuit.
figure 2

a, Amplitude of the radiofrequency tank voltage as a function of the d.c. magnetic bias of the qubit, fxd.c., for a microwave driving frequency ωd/2π=14.125 GHz and various amplitudes of the radiofrequency current driving the tank circuit. b, The height of the peaks (squares) and dips (circles) as a function of the voltage amplitude of the unloaded tank circuit VT0. The voltage VT0 is determined as VT taken at fxd.c.=0.02 where the effect of the interaction between the tank circuit and the qubit is negligible. The height saturates near 200 nV.

Full size image

The results for the second type of experiment are shown in Fig. 3. The comparison shows that at the bias point corresponding to maximum Sisyphus damping, the resonant line widens in good agreement with the results for the driven LC circuit. At the bias point corresponding to maximum amplification, the line narrows, indicating a tendency towards lasing. We can extract the quality factors in these two regimes, as well as for the bias point far from the resonance where no extra damping occurs. The comparison of the experimental results with equation (5) of the Methods section section shows a quantitative agreement.

Figure 3: Influence of the driven qubit on the spectral properties of the LC circuit.
figure 3

a, Spectral density of the voltage noise in the LC circuit, SV(ω), measured when the low-frequency radiofrequency driving is switched off while the high-frequency qubit driving is fixed at ωd/2π=6 GHz. SV is shown as a function of frequency (vertical axis) and normalized magnetic flux in the qubit fxd.c. (horizontal axis). b, The integral, , evaluated using the data from a, and expressed as the effective temperature of the tank circuit Ttank. At the optimal d.c. bias fxd.c., the effective temperature is lower by 8% than the temperature T0 away from the resonance, (T0−Ttank)/T0=0.08. c, Spectral density SV(ω) measured at three different values of fxd.c. corresponding to damping (blue), amplification (red) and away from the resonance (black). These values of fxd.c. are marked, respectively, by blue, red and black arrows in a.

Full size image

Finally, the results shown in Fig. 3 enable us to estimate the efficiency of the cooling or amplification (lasing) in the two regimes. Integrating the power spectra, we observe that in the damping regime the number of photons in the LC circuit decreases by about 8% compared with the undamped case. A cooling effect of 6%–13% was observed also for other microwave frequencies. One reason why there is only little cooling lies in the fact that our system is optimized towards maximum Sisyphus damping rather than minimum temperature. Indeed, damping is optimized when the resonant point is reached at the turning point of the oscillator’s trajectory. In this regime, even a small reduction of the oscillator’s amplitude, that is, weak cooling, switches the whole mechanism off. For more efficient cooling, we could imagine a feedback mechanism in which the detuning is slightly reduced when the 10% cooling is reached. This would bring the system again into the optimal damping regime with extra cooling.

In our experiments, the qubit’s temperature is low, Tq<100 mK, but the tank circuit is strongly coupled to the amplifier anchored at the T0≈4.2 K stage of the refrigerator. The two orders of magnitude mismatch between the energy level separation of the qubit Δ/h≥3.5 GHz and that of the LC circuit ωT/2π≈20 MHz makes the coupling between them inefficient for heat transfer. Thus, without active cooling, the oscillator would adopt the high temperature of the amplifier, Ttank≈T0. What we have demonstrated experimentally is the reduction of Ttank by the active Sisyphus cooling by approximately 10% as compared with T0. Potentially, a much stronger cooling could be achieved by first optimizing the Sisyphus cooling as discussed above and then, at a second stage, by switching to, for example, the sideband resolved cooling which could produce Ttank∼(ωT/ωd)Tq≈0.1 mK (ref. 17). Furthermore, the initial temperature of the tank circuit could be reduced by decoupling it from the amplifier, for example, by a radiofrequency isolator. (Unfortunately, cryogenic isolators for the 20–100 MHz range are not available commercially.) Finally, we expect to gain if, instead of measuring the low-frequency oscillator directly by an amplifier, we infer the information on its state by dispersively measuring the qubit by microwaves in the gigahertz range18,19,20.

To develop the comparison further, we model the Sisyphus damping as an extra effective bath coupled to the oscillator, which we characterize by a quality factor QSis and temperature TSis. The standard analysis gives the total quality factor and temperature, Qtank−1=Q0−1+QSis−1 and TtankQtank−1=T0Q0−1+TSisQSis−1, respectively. Here, T0 is the temperature of the oscillator without Sisyphus damping, which in our case is determined mostly by the amplifier. Our data show that Qtank∼Q0/2. Thus, the coupling strength of the Sisyphus mechanism is comparable to that of the rest of the environment, QSis≈Q0≈340. In the present experiment, it seems that TSis is comparable to T0, consistent with the observation that we have little cooling.

In contrast, in the amplification mode of our experiment, the line gets much sharper, which can be formally expressed by choosing QSis negative, QSis≈−600. This means that, although the system did not yet reach the lasing instability, because |QSis|>Q0, it is not far from it. Consistently, the Sisyphus mechanism, acting as an active medium with population inversion, is described by a negative temperature TSis. Its value is not known, but we can get a lower bound for it from the inequality Ttank/Qtank>T0/Q0. This predicts that the temperature and number of photons should be increased by a factor ∼2. The experiment shows a 36% increase, which demonstrates the trend, although a quantitative discrepancy remains.

We now outline the theoretical analysis of the problem. Quantizing the oscillations in the tank circuit, we arrive at the Hamiltonian

where the coupling constant is g=M IpIT,0 and is the amplitude of the vacuum fluctuation of the current in the LC oscillator. The third term of equation (1) describes the high-frequency driving with amplitude ΩR0. After transformations to the eigenbasis of the qubit and some appropriate approximations (described in the Methods section), the Hamiltonian reduces to

with and tanζ≡ɛ/Δ. Thus, we obtain the effective Rabi frequency ΩR0cosζ and the effective linear qubit–oscillator coupling gsinζ. As we need both of these terms for the Sisyphus cooling, the qubit should be biased near but not exactly at the symmetry point. The second-order term ∝g2 is responsible, for example, for the qubit-dependent shift of the oscillator frequency16.

We account for the effects of dissipation by the Liouville equation for the density operator of the system, including the two relevant damping terms,

As far as the qubit is concerned (LQ), we consider spontaneous emission with rate ΓR and pure dephasing with rate Γϕ* (see the Methods section). The damping of the tank circuit (LR) is characterized by the friction coefficient κ=ωT/Q0 and effective temperature T0 (see the Methods section). We solve the master equation (3) in the quasiclassical limit, that is, for n≡〈a†a〉≫1, and for various choices of the parameters ΓR, Γϕ* and ΩR0. As the system is harmonically driven, we determine the response of the observables/density matrix at the driving frequency, and, finally, find the amplitude of the driven voltage oscillations across the tank circuit. As shown in Fig. 4, we reproduce well the experimental findings by fitting the system parameters within a reasonable range. Actually, a good fit can be obtained for a relatively wide range of values of the Rabi frequency ΩR0 and pure dephasing rate Γϕ*, provided their product is kept roughly constant. On the other hand, the relaxation rate ΓR is determined rather accurately.

Figure 4: Amplitude of the voltage oscillation for various amplitudes of the radiofrequency driving of the tank circuit.
figure 4

Coloured lines: experimental data. Black lines: numerical solution of equations (3) for ΩR0=2π×0.5 GHz, ΓR=1.0×108 s−1, Γϕ*=5.0×109 s−1. The amplitude of the radiofrequency driving is directly related to the asymptotic value of voltage at fxd.c.=0.02. The central dip is due to the quadratic coupling term in (2) that causes a shift of the oscillator frequency16.

Full size image

The Sisyphus cooling and amplification by a superconducting qubit analysed here can also be applied to nanoelectromechanical systems8,21,22,23,24,25. Typical nanomechanical resonators in the frequency range of 10–100 MHz can be coupled to Josephson qubits with coupling strength comparable to that of our system. Owing to typically higher quality factors of nanoelectromechanical systems, more efficient cooling and lasing should be possible.

Methods

Estimating the quality factor

Here, we provide a qualitative analysis of the first type of measurement, the response analysis. The LC tank circuit is driven by a current source with amplitude ITd, and the resulting amplitude VT of the voltage oscillations across the tank circuit is measured. It is

where is the actual amplitude of the radiofrequency current in the inductance and Qtank is the effective quality factor of the tank circuit. It is given by the ratio Qtank=2πWT/A between the energy stored in the tank, WT=LTIT2/2, and the energy loss A per period. The latter consists of two contributions, A=AT+ASis. The intrinsic losses of the tank are given by AT=2πWT/Q0, where Q0 is the intrinsic quality factor of the tank circuit. To estimate the average work done by the tank on the qubit per period, ASis, we consider the optimal situation when the oscillator brings the qubit into resonance at the turning point of its trajectory (Fig. 1). We assume further that the state of the qubit is instantaneously ‘thermalized’, with equal probabilities to remain in the ground state or to get excited. In the latter case, after leaving the area of resonance, the qubit can relax with rate ΓR. The probability of the qubit relaxing during one period 2π/ωT within an interval dt is given by dP=exp(−ΓRt) ΓRdt. With Ir.f.(t)=−ITcos(ωTt) and dASis=M IpdIr.f., we obtain the Sisyphus work carried out by the oscillator in this event to be 2M IpIT (1−cos(ωTt)), where the factor 2 is due to the work carried out after the relaxation. Thus, we obtain the value of the work averaged over many cycles (taking into account the probability 1/2 of the initial state to be excited)

where

This estimate demonstrates that the optimal situation for damping or amplification is reached when ΓR∼ωT. For the effective quality factor, we obtain

where ± stands for damping/amplification. Substituting into equation (4), we arrive at

where VT0=Q0ωTLTITd is the voltage on the tank circuit far from resonance. Equation (6) provides the estimate for the increase/decrease of the tank voltage for large driving currents ITd, such that the qubit spends most of the time away from the resonant excitation area. For weaker driving, when the times spent away and within the excitation area are comparable, the damping is weaker.

Transformations of the Hamiltonian

After transformation to the eigenbasis of the qubit, the Hamiltonian (1) becomes

with tanζ=ɛ/Δ and . Because of the large difference of the energy scales between the qubit and the oscillator, ΔE≫ℏωT, we can drop within the usual rotating-wave approximation, the longitudinal driving term −ℏΩR0cos(ωdt)sinζ σz. On the other hand, we retain the transverse coupling term, −gcosζ σx(a+a†), but transform it by using a Schrieffer–Wolff transformation, US=exp(i S), with generator S=(g/ΔE)cosζ (a+a†) σy, into a second-order longitudinal coupling. The Hamiltonian then reduces to the form (2).

Dissipation in the system

The dynamics of the system is strongly influenced by dissipation. The qubit’s dissipation is well described by the Lindblad form

We can neglect excitation processes because the qubit’s energy splitting exceeds the temperature. Thus, the standard longitudinal relaxation rate is given by T1−1=ΓR. The rates ΓR and Γϕ* may depend on the working point, that is, on ζ. In the experiments considered here, this point is fixed by the driving frequency by the condition ℏωd≈ΔE. As cooling and amplification appear only in the narrow vicinity of this point, and for all other values of the bias the qubit is in the ground state and its response does not depend on the relaxation rates, it is reasonable to use single values for both ΓR and Γϕ*. It should be mentioned that pure dephasing is frequently caused by the 1/f noise26, for which the Markovian description used here is not applicable. We expect, however, that the main features are still captured provided Γϕ* is chosen properly.

In addition, the resonator damping term can be written in the usual form27,

where κ=ωT/Q0 characterizes the strength of the resonator damping and Nth=[exp(ℏωT/kBT0)−1]−1 is the thermal average number of photons in the resonator.