Abstract
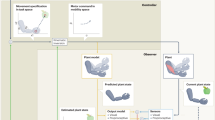
Unifying principles of movement have emerged from the computational study of motor control. We review several of these principles and show how they apply to processes such as motor planning, control, estimation, prediction and learning. Our goal is to demonstrate how specific models emerging from the computational approach provide a theoretical framework for movement neuroscience.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Bellman, R. Dynamic Programming (Princeton Univ. Press, Princeton, New Jersey, 1957).
Shadmehr, R. & Mussa-Ivaldi, F. Adaptive representation of dynamics during learning of a motor task. J. Neurosci. 14, 3208–3224 (1994).
Wolpert, D. M., Ghahramani, Z. & Jordan, M. I. An internal model for sensorimotor integration. Science 269, 1880–1882 ( 1995).
Ghahramani, Z. & Wolpert, D. M. Modular decomposition in visuomotor learning. Nature 386, 392– 395 (1997).
Gomi, H. & Kawato, M. Equilibrium-point control hypothesis examined by measured arm stiffness during multijoint movement. Science 272, 117–120 ( 1996).
Cohn, J. V., DiZio, P. & Lackner, J. R. Reaching during virtual rotation: context specific compensations for expected coriolis forces. J. Neurophysiol. 83, 3230–3240 (2000).
Flash, T. & Hogan, N. The co-ordination of arm movements: An experimentally confirmed mathematical model. J. Neurosci. 5, 1688–1703 (1985).
Uno, Y., Kawato, M. & Suzuki, R. Formation and control of optimal trajectories in human multijoint arm movements: Minimum torque-change model. Biol. Cybern. 61, 89–101 ( 1989).
Harris, C. M. & Wolpert, D. M. Signal-dependent noise determines motor planning. Nature 394, 780– 784 (1998).
Kitazawa, S., Kimura, T. & Yin, P. Cerebellar complex spikes encode both destinations and errors in arm movements . Nature 392, 494–497 (1998).
Feldman, A. G. Functional tuning of the nervous system with control of movement or maintenance of a steady posture. III. Mechanographic analysis of execution by arm of the simplest motor tasks. Biophysics 11, 766 –775 (1966).
Bizzi, E., Accornerro, N., Chapple, B. & Hogan, N. Posture control and trajectory formation during arm movement. J. Neurosci. 4, 2738–2744 (1984).
Hogan, N. An organizing principle for a class of voluntary movements. J. Neurosci. 4, 2745–2754 ( 1984).
Flash, T. The control of hand equilibrium trajectories in multi-joint arm movements . Biol. Cybern. 57, 257– 274 (1987).
Kawato, M., Furawaka, K. & Suzuki, R. A hierarchical neural network model for the control and learning of voluntary movements. Biol. Cybern. 56, 1–17 (1987).
Giszter, S. F., Mussa-Ivaldi, F. A. & Bizzi, E. Convergent force fields organized in the frog's spinal cord. J. Neurosci. 13, 467– 491 (1993).
Tresch, M. C., Saltiel, P. & Bizzi, E. The construction of movement by the spinal cord. Nat. Neurosci. 2, 162–167 (1999).
Mussa-Ivaldi, F. A. Modular features of motor control and learning. Curr. Opin. Neurobiol. 9, 713–717 ( 1999).
Mussa-Ivaldi, F. A. Do neurons in the motor cortex encode movement direction? An alternative hypothesis . Neurosci. Lett. 91, 106– 111 (1988).
Sanger, T. Theoretical considerations for the analysis of population coding in motor cortex. Neural Comput. 6, 29– 37 (1994).
Georgopoulos, A. P. Current issues in directional motor control. Trends Neurosci. 18, 506–510 (1995).
Scott, S. & Kalaska, J. F. Motor cortical activity is altered by changes in arm posture for identical hand trajectories. J. Neurophysiol. 73, 2563–2567 ( 1995).
Kakei, S., Hoffman, D. S. & Strick, P. L. Muscle and movement representations in the primary motor cortex. Science 285, 2136– 2139 (1999).
Todorov, E. Direct cortical control of muscle activation in voluntary arm movements: a model. Nat. Neurosci. 3, 391– 398 (2000).
Goodwin, G. C. & Sin, K. S. Adaptive Filtering Prediction and Control (Prentice-Hall, Englewood Cliffs, New Jersey, 1984).
van Beers, R. J., Sittig, A. C. & van der Gon, J. J. D. Integration of proprioceptive and visual position-information: An experimentally supported model. J. Neurophysiol. 81, 1355–1364 (1999).
Kuo, A. D. An optimal-control model for analyzing human postural balance. IEEE Trans. Biomed. Eng. 42, 87–101 (1995).
Merfeld, D. M., Zupan, L. & Peterka, R. J. Humans use internal model to estimate gravity and linear acceleration. Nature 398, 615– 618 (1999).
Wolpert, D. M., Goodbody, S. J. & Husain, M. Maintaining internal representations: the role of the superior parietal lobe. Nat. Neurosci. 1, 529–533 (1998).
Miall, R. C. & Wolpert, D. M. Forward models for physiological motor control. Neural Networks 9, 1265– 1279 (1996).
Johansson, R. S. & Cole, K. J. Sensory-motor coordination during grasping and manipulative actions. Curr. Opin. Neurobiol. 2, 815–823 ( 1992).
Sirigu, A. et al. The mental representation of hand movements after parietal cortex damage. Science 273, 1564– 1568 (1996).
Bell, C. C., Han, V. Z., Sugawara, Y. & Grant, K. Synaptic plasticity in a cerebellum-like structure depends on temporal order. Nature 387, 278–281 ( 1997).
Duhamel, J. R., Colby, C. L. & Goldberg, M. E. The updating of the representation of visual space in parietal cortex by intended eye movements. Science 255, 90–92 (1992).
Blakemore, S. J., Frith, C. D. & Wolpert, D. M. Perceptual modulation of self-produced stimuli: The role of spatio-temporal prediction. J. Cogn. Neurosci. 11, 551–559 (1999).
Frith, C. D. The Cognitive Neuropsychology of Schizophrenia (Lawrenece Erlbaum, Hove, UK, 1992).
Sirigu, A., Daprati, E., Pradatdiehl, P., Franck, N. & Jeannerod, M. Perception of self-generated movement following left parietal lesion. Brain 122, 1867–1874 (1999).
Wolpert, D. M. & Kawato, M. Multiple paired forward and inverse models for motor control. Neural Networks 11, 1317–1329 (1998).
Eskandar, E. N. & Assad, J. A. Dissociation of visual, motor and predictive signals in parietal cortex during visual guidance . Nat. Neurosci. 2, 88– 93 (1999).
Kim, J. & Shadlen, M. N. Neural correlates of a decision in the dorsolateral prefrontal cortex of the macaque. Nat. Neurosci. 2, 176–185 ( 1999).
Kawato, M. & Gomi, H. The cerebellum and VOR/OKR learning models. Trends Neurosci. 15, 445– 453 (1992).
Shidara, M., Kawano, K., Gomi, H. & Kawato, M. Inverse-dynamics encoding of eye movement by Purkinje cells in the cerebellum. Nature 365, 50–52 ( 1993).
Lackner, J. R. & DiZio, P. Rapid adaptation to Coriolis force perturbations of arm trajectory. J. Neurophysiol. 72, 299–313 ( 1994).
Conditt, M. A., Gandolfo, F. & Mussa-Ivaldi, F. A. The motor system does not learn dynamics of the arm by rote memorization of past experience. J. Neurophysiol. 78, 554–560 (1997).
Conditt, M. A. & Mussa-Ivaldi, F. A. Central representation of time during motor learning. Proc. Natl. Acad. Sci. USA 96, 11625–11630 (1999).
Bhushan, N. & Shadmehr, R. Computational nature of human adaptive control during learning of reaching movements in force fields. Biol. Cybern. 81, 39–60 (1999).
Brashers-Krug, T., Shadmehr, R. & Bizzi, E. Consolidation in human motor memory. Nature 382, 252–255 ( 1996).
Gandolfo, F., Mussa-Ivaldi, F. A. & Bizzi, E. Motor learning by field approximation. Proc. Natl. Acad. Sci. USA 93, 3843–3846 (1996).
Krakauer, J. W., Ghilardi, M. F. & Ghez, C. Independent learning of internal models for kinematic and dynamic control of reaching. Nat. Neurosci. 2, 1026–1031 (1999).
Flanagan, J. R. et al. Composition and decomposition of internal models in motor learning under altered kinematic and dynamic environments. J. Neurosci. 19, B1–B5 ( 1999).
Acknowledgements
We thank Pierre Baraduc, Robert van Beers, James Ingram, Kelvin Jones and Philipp Vetter for comments on the manuscript. This work was supported by grants from the Wellcome Trust, the Gatsby Charitable Foundation and the Human Frontiers Science Organization.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Wolpert, D., Ghahramani, Z. Computational principles of movement neuroscience. Nat Neurosci 3 (Suppl 11), 1212–1217 (2000). https://doi.org/10.1038/81497
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/81497
This article is cited by
-
Motor neurons generate pose-targeted movements via proprioceptive sculpting
Nature (2024)
-
Prediction error in implicit adaptation during visually- and memory-guided reaching tasks
Scientific Reports (2024)
-
The complex interplay between perception, cognition, and action: a commentary on Bach et al. 2022
Psychological Research (2024)
-
Impairment of the internal forward model and feedback mechanisms for vocal sensorimotor control in post-stroke aphasia: evidence from directional responses to altered auditory feedback
Experimental Brain Research (2024)
-
Theoretical explanations and the availability of information for learning via combined action observation and motor imagery: a commentary on Eaves et al. (2022)
Psychological Research (2024)