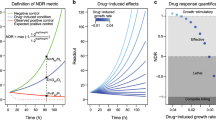
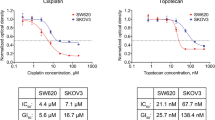
Abstract
In vitro cell proliferation assays are widely used in pharmacology, molecular biology, and drug discovery. Using theoretical modeling and experimentation, we show that current metrics of antiproliferative small molecule effect suffer from time-dependent bias, leading to inaccurate assessments of parameters such as drug potency and efficacy. We propose the drug-induced proliferation (DIP) rate, the slope of the line on a plot of cell population doublings versus time, as an alternative, time-independent metric.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Change history
13 May 2016
In the version of this article initially published online, two funding sources were not listed in the Acknowledgments. The sentence "This work was also supported by the National Science Foundation (grant MCB-1411482 to C.F.L.) and the VICC (Young Ambassador Award to C.F.L.)." was added prior to the last sentence in the Acknowledgments.
References
Zuber, J. et al. Nat. Biotechnol. 29, 79–83 (2011).
Berns, K. et al. Nature 428, 431–437 (2004).
Bonnans, C., Chou, J. & Werb, Z. Nat. Rev. Mol. Cell Biol. 15, 786–801 (2014).
Garnett, M.J. et al. Nature 483, 570–575 (2012).
Wang, L., McLeod, H.L. & Weinshilboum, R.M. N. Engl. J. Med. 364, 1144–1153 (2011).
Barretina, J. et al. Nature 483, 603–607 (2012).
Stephenson, R.P. Br. J. Pharmacol. Chemother. 11, 379–393 (1956).
Fallahi-Sichani, M., Honarnejad, S., Heiser, L.M., Gray, J.W. & Sorger, P.K. Nat. Chem. Biol. 9, 708–714 (2013).
Yang, W. et al. Nucleic Acids Res. 41, D955–D961 (2013).
Goutelle, S. et al. Fundam. Clin. Pharmacol. 22, 633–648 (2008).
Tyson, D.R., Garbett, S.P., Frick, P.L. & Quaranta, V. Nat. Methods 9, 923–928 (2012).
Frick, P., Paudel, B., Tyson, D. & Quaranta, V. J. Cell. Physiol. 230, 1403–1412 (2015).
Shoemaker, R.H. Nat. Rev. Cancer 6, 813–823 (2006).
Quaranta, V. et al. Methods Enzymol. 467, 23–57 (2009).
Gong, Y. et al. PLoS Med. 4, e294 (2007).
Seashore-Ludlow, B. et al. Cancer Discov. 5, 1210–1223 (2015).
Rees, M.G. et al. Nat. Chem. Biol. 12, 109–116 (2016).
McDermott, U., Sharma, S.V. & Settleman, J. Methods Enzymol. 438, 331–341 (2008).
Heiser, L.M. et al. Genome Biol. 10, R31 (2009).
Sporn, M.B. & Harris, E.D. Jr. Am. J. Med. 70, 1231–1235 (1981).
Seber, G.A.F. & Wild, C.J. Nonlinear Regression (Wiley, 2003).
Ritz, C. & Streibig, J.C. J. Stat. Softw. 12, 1–22 (2005).
Cornish-Bowden, A. Fundamentals of Enzyme Kinetics 4th edn. (Wiley-Blackwell, 2012).
Rein, M. Phys. Fluids A Fluid Dyn. 4, 873–886 (1992).
Soetaert, K., Petzoldt, T. & Setzer, R.W. J. Stat. Softw. 33, 1–25 (2010).
Acknowledgements
We are grateful to R. Feroze, J. Hao, K. Jameson, and C. Peng for support in experimental data acquisition; to J. Guinney, T. de Paulis, and J.R. Faeder for critical reviews of the manuscript; to W. Pao (Vanderbilt University, Nashville, Tennessee) for providing the PC9 cell line; and to M. Herlyn (Wistar Institute, Philadelphia, Pennsylvania) for providing the WM115 cell line. This work was supported by Uniting Against Lung Cancer 13020513 (D.R.T.), Vanderbilt Biomedical Informatics Training Program NLM 5T15-LM007450-14 (L.A.H.), and the National Cancer Institute U54-CA113007 (V.Q.), U01-CA174706 (V.Q.), and R01-CA186193 (V.Q.), and partially supported by the National Cancer Institute (P50-CA098131) and the National Center for Advancing Translational Sciences (UL1-TR000445-06). This work was also supported by the National Science Foundation (grant MCB-1411482 to C.F.L.) and the VICC (Young Ambassador Award to C.F.L.). Its contents are solely the responsibility of the authors and do not necessarily represent official views of the National Cancer Institute, the National Center for Advancing Translational Sciences, or the National Institutes of Health.
Author information
Authors and Affiliations
Contributions
D.R.T., L.A.H., P.L.F., and S.P.G. conceived and designed the study; D.R.T., L.A.H., and S.P.G. built the mathematical models and performed simulations; B.B.P., K.N.H., and P.L.F. acquired experimental data; D.R.T., L.A.H., P.L.F., and S.P.G. analyzed and interpreted the experimental data; C.F.L., D.R.T., L.A.H., P.L.F., S.P.G., and V.Q. wrote, reviewed, and/or revised the manuscript; and C.F.L., D.R.T., and V.Q. supervised the study.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Integrated supplementary information
Supplementary Figure 1 Different formulations of the dose–response curve.
Potency parameters EC50 and IC50 are shown, as are area under the curve (AUC) and activity area (AA; the inverse of AUC), parameters that attempt to capture both potency and efficacy in a single quantity. (a) The “scaled” form given in equation (S2); (b) The “direct effect” form obtained by rearranging equation (S2) to solve for Edrug; (c) The “response ratio” form obtained by dividing the direct-effect form by E0. Note that we consider here a case where Emax < 0, which is possible when using a dynamic drug effect metric such as DIP rate. This results in IC50 < EC50 (see equation S5). In cases like this, the IC50 is sometimes referred to as the GI50 (half-maximal growth inhibitory concentration; see Supplementary Table 1).
Supplementary Figure 2 Fast-acting drugs, slow-acting drugs, and DIP rate.
Hypothetical growth curves (in log scale) for a cell line untreated and treated with two different drugs: a fast-acting drug where the full effect is achieved immediately, and a slow-acting drug that causes a temporal delay in the stabilization of the drug effect. Also shown is drug-induced proliferation (DIP) rate, defined as the slope of the line after the drug effect has stabilized (in this case, immediately for the fast-acting drug and ≥48h for the slow-acting drug). Note that the DIP rate is shown as equivalent for both the fast- and slow-acting drugs for illustration purposes only.
Supplementary Figure 3 Two-state model of fractional proliferation predicts a sigmoidal relationship between proliferation rate and drug concentration.
(a) The model assumes two states, a drug-naïve state and a drugged state, each with its own characteristic rate of proliferation (DIP0 and DIPmax, respectively), which is the difference between the rates of cell division and death. The rate of transition from the drug-naïve state to the drugged state depends on the concentration of drug, while the reverse transition does not. Hence, as the concentration of drug increases, the dynamic equilibrium between states shifts increasingly in favor of the drugged state. (b) Since the action of an antiproliferative drug is to reduce, and perhaps reverse, the rate of proliferation of a cell population, we assume that the proliferation rate of the drug-naïve state is positive and greater than that of the drugged state (which may be positive or negative). In Figure 1 of the main text, we assume that in each case the drug is cytotoxic at saturating drug concentrations (i.e., causes regression of the cell population). Hence, the DIP rate of the drugged state (DIPmax) is assumed to be negative. (c) An example dose–response curve predicted by the two-state model under the partial equilibrium assumption (PEA). The curve was generated from equation (S27) with EC50 = 1e–8 M, DIP0 = 0.06*ln(2) h-1, and DIPmax = –0.03*ln(2) h-1. (d) An example dose–response curve predicted by the two-state model in conditions where the PEA does not hold. The curve was generated by numerical integration of equations (S12) and (S13) with kon = 1e5 M-1 h-1, koff = 1e–3 h-1, kdiv– kdeath = 0.06*ln(2) h-1, and kdiv* – kdeath* = –0.03*ln(2) h-1. Note that these are consistent with the values used in part (c); see equations (S22), (S23), and (S26). Arrows highlight largest differences between calculated values (circles) and the Hill equation fit (black line).
Supplementary Figure 4 Theoretical illustration of bias in dose–response curves based on the NCI DTP dynamic drug effect metric.
(a) Growth curves in the absence and presence of 630 nM drug for the theoretical fast-growing cell line with delayed drug effect (Fig. 1c in the main text). Dash-dotted lines are a visual illustration of the NCI DTP dynamic metric and the time-dependent bias that it harbors. Depending on when cell count measurements are taken, the NCI DTP metric can indicate that the drug is partially cytostatic (<96h), fully cytostatic (96h), or cytotoxic (>96h) at this concentration. (b) Comparison of dose–response curves for this cell line and drug type based on the NCI DTP dynamic effect metric and DIP rate. The vertical orange line corresponds to 630 nM drug concentration; circles correspond to those in part (a).
Supplementary Figure 5 Static-based dose–response curves for PC9 parental cells and subclones treated with erlotinib.
Dose–response curves for three PC9-derived drug-sensitive (DS) clonal sublines (DS3, DS4, DS5) and parental PC9 cells treated with erlotinib using cell counts after 72h drug exposure as the drug effect metric. Filled circles are mean values (n ≥ 6), lines are optimal fits to a four-parameter log-logistic model (equation S2), and grey shading indicates 95% confidence intervals on the fitting function. None of the dose–response curves for the clonal sublines is statistically different from the parental curve based on t-statistics and the null hypothesis that the ratio of clonal to parental values is 1 (p>0.05 for each of the four fitting parameters).
Supplementary Figure 6 Automated estimation of DIP rate from cell count data.
Cell count data for the three PC9 sublines treated with 3 μM erlotinib (Fig 2c of the main text) is used to evaluate the ability to automatically estimate drug effect stabilization times and DIP rates using adjusted R2 and root-mean-squared error (RMSE) as measures of linearity. Best linear model fits to the population growth curves (solid red lines) are based on the RMSE-estimated stabilization times. A fifth-order polynomial (solid blue line) was fit to the RMSE curve and used to estimate the point at which exclusion of additional data points does not substantially improve the linear model fit. Source code implementing this approach (dipDRC.r) is freely available at github.com/QuLab-VU/DIP_rate_NatMeth2016. See Supplementary Note for more details.
Supplementary Figure 7 Effects of sampling frequency on automated DIP rate estimation.
Cell count data for one PC9 subline (DS3) treated with 3 μM erlotinib (Fig 2c of the main text and Supplementary Fig. 6) is used to evaluate the robustness of the automated DIP rate estimation method to changes in sampling frequency. The full data set (top row) was successively subsampled a total of four times. Best linear model fits (solid red lines) are based on the adjusted R2-estimated stabilization times. DIP rates for data sets with ≥15 data points varied by less than 1%; DIP rate from the smallest data set (n=8) was within 15% of that for the full data set. Gray shading indicates 95% confidence interval on the DIP rate. See Supplementary Note and Supplementary Figure 6 for more details.
Supplementary Figure 8 Theoretical effects of variations around a mean cell seeding density on the static effect metric and response ratio.
The two-state model of fractional proliferation (Supplementary Note and Supplementary Fig. 3) with the “fast proliferating / fast acting” parameter set (Supplementary Table 2) is seeded with initial cell counts drawn from a normal distribution with mean 1 and standard deviation 0.1 and simulated under untreated and drug-treated conditions. (a) 100 simulated time courses each of untreated and drug-treated cell populations. (b) Boxplots of static response ratios at 72h for variations in seeding density alone and variations in seeding density and measurement time (72 ± 5h). Based on 108 samples. Red line is the median; black dot is the mean; boxes extend from the first to third quartile; whiskers extend 1.5 times the interquartile range; outliers are not shown. (c) For variations in the seeding density alone, histograms for the mean of 10 untreated final (72h) cell counts (n=104; left column), the drug-treated final cell count (n=104; middle column), and the static response ratio (n=108; right column). Sample means, standard deviations, and skews are shown in each case. Analytical distributions are shown in red (equations S30, S32, and S33). (d) Same as c (less the analytical distributions) but for variations in both seeding density and measurement time (72 ± 5h).
Supplementary Figure 9 Effects of variations in mean cell seeding density on DIP rate estimation.
Cell count data for BRAF-mutant (SKMEL5) melanoma cells treated with 8 μM PLX4720 is used to evaluate the effects of mean seeding density on DIP rate estimates. Cell counts were obtained using fluorescence microscopy imaging (Online Methods). (a) Population growth curves (log2 scaled) for each seeding density considered (n=4; seeding density in cells/well is listed above each plot). Vertical dashed line corresponds to ~72h, the hand-chosen stabilization time; data to the right of this point were used to estimate DIP rate. (b) Population growth curves from part (a) normalized to the number of cells for each well at the first time point. Vertical dashed line corresponds to ~72h. (c) Boxplots of estimated DIP rates (n=4) at each seeding density. Mean values were statistically indistinguishable across all seeding densities (p=0.47); variances were not (Levene’s test, p=0.0082), as expected (see Supplementary Note).
Supplementary information
Supplementary Text and Figures
Supplementary Figures 1–9, Supplementary Tables 1 and 2, and Supplementary Note (PDF 2671 kb)
Supplementary Software
Software for obtaining DIP rates automatically from raw cell count data. (ZIP 0 kb)
Rights and permissions
About this article
Cite this article
Harris, L., Frick, P., Garbett, S. et al. An unbiased metric of antiproliferative drug effect in vitro. Nat Methods 13, 497–500 (2016). https://doi.org/10.1038/nmeth.3852
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nmeth.3852
This article is cited by
-
Quick tips for interpreting cell death experiments
Nature Cell Biology (2023)
-
Analysis and modeling of cancer drug responses using cell cycle phase-specific rate effects
Nature Communications (2023)
-
A global sensitivity analysis of a mechanistic model of neoadjuvant chemotherapy for triple negative breast cancer constrained by in vitro and in vivo imaging data
Engineering with Computers (2023)
-
Multiplexed and reproducible high content screening of live and fixed cells using Dye Drop
Nature Communications (2022)
-
Enhanced phosphorylation of c-Jun by cisplatin treatment as a potential predictive biomarker for cisplatin response in combination with patient-derived tumor organoids
Laboratory Investigation (2022)