Abstract
The origin of magnetism in metals has been traditionally discussed in two diametrically opposite limits: itinerant and local moments. Surprisingly, there are very few known examples of materials that are close to the itinerant limit, and their properties are not universally understood. In the case of the two such examples discovered several decades ago, the itinerant ferromagnets ZrZn2 and Sc3In, the understanding of their magnetic ground states draws on the existence of 3d electrons subject to strong spin fluctuations. Similarly, in Cr, an elemental itinerant antiferromagnet with a spin density wave ground state, its 3d electron character has been deemed crucial to it being magnetic. Here, we report evidence for an itinerant antiferromagnetic metal with no magnetic constituents: TiAu. Antiferromagnetic order occurs below a Néel temperature of 36 K, about an order of magnitude smaller than in Cr, rendering the spin fluctuations in TiAu more important at low temperatures. This itinerant antiferromagnet challenges the currently limited understanding of weak itinerant antiferromagnetism, while providing insights into the effects of spin fluctuations in itinerant–electron systems.
Similar content being viewed by others
Introduction
The local and itinerant moment are extreme limits of magnetic behaviour, with poorly understood physics associated with in-between scenarios. While the local moment magnetism (or real-space-localized magnetic moments and fluctuations) was readily understood early on within the Heisenberg model1 using a Weiss molecular field, the itinerant moment behaviour (corresponding to moments and fluctuations localized in the reciprocal space) can only partially be reproduced by current theoretical approaches. Despite the success of the Stoner model2 and the subsequent improvements when spin fluctuations were accounted for3,4,5, a unified picture of magnetism (which to encompass both extreme scenarios, local and itinerant moment) remains elusive. A practical limitation is the small number of known itinerant moment magnetic systems. In one extreme case, that of magnetic metals without magnetic constituents, only two itinerant ferromagnets (IFMs), Sc3In (ref. 6) and ZrZn2 (ref. 7), have been known for 50 years.
Here we report evidence for an itinerant antiferromagnet (IAFM) with no magnetic constituents, TiAu. Given the small number of known itinerant magnets, the discovery of the IAFM TiAu provides an opportunity for detailed studies which to advance the understanding of the physics of itinerant magnets in general, and of IAFMs in particular. Thermodynamic and transport measurements reveal the antiferromagnetic order at a Néel temperature TN≅36 K. The long-range order is confirmed by neutron diffraction data, while muon spin relaxation (μSR) experiments indicate static order. Together these measurements point to small moment ordering in the whole sample volume. In addition to the experimental evidence for the itinerant moment antiferromagnetic order in TiAu, density functional theory (DFT) calculations confirm the spin density wave (SDW) small moment ordering.
Results
Evidence for itinerant moment antiferromagnetic order
TiAu has been reported to form in three distinct crystal structures, cubic Pm m8, tetragonal P4/nmm9 and orthorhombic Pmma8, posing an inherent difficulty in synthesizing it as a single phase. It comes as no surprise then, that no reports of physical properties of TiAu exist. Here we report the magnetic and electronic properties of phase-pure orthorhombic TiAu, and that it is an itinerant electron antiferromagnet.
m8, tetragonal P4/nmm9 and orthorhombic Pmma8, posing an inherent difficulty in synthesizing it as a single phase. It comes as no surprise then, that no reports of physical properties of TiAu exist. Here we report the magnetic and electronic properties of phase-pure orthorhombic TiAu, and that it is an itinerant electron antiferromagnet.
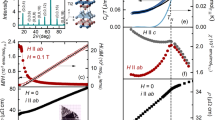
The first evidence for the antiferromagnetic ground state is the cusp around 36 K in the temperature-dependent magnetic susceptibility M(T)/H, shown in Fig. 1 (left axis). By analogy with local moment AFMs, the TiAu zero-field-cooled and field-cooled data are indistinguishable. The value of the temperature-independent Pauli susceptibility, calculated from the magnetic density of states χ0≈0.2 × 10−3 e.m.u. mol−1, agrees well with the experimental one M0/H≈0.3 × 10−3 e.m.u. mol−1. Upon warming above the Néel temperature, the inverse susceptibility H/(M–M0) (right axis, Fig. 1) is linear in temperature up to 800 K. Such linear T dependence of H/M has been long considered the hallmark of local moment magnetism, until it was observed in the weak IFMs without local moments, ZrZn2 (ref. 7) and Sc3In (ref. 6). Puzzling at first, the origin of this behaviour was reconciled in the case of IFMs, when spin fluctuation effects were considered by Moriya3,4. The self-consistent renormalization theory unified the local and itinerant pictures of ferromagnetism, and postulated a new origin for the Curie–Weiss-like susceptibility in the latter, as the interactions of the spatially extended modes of spin fluctuations10,11. TiAu however is an IAFM, and no existing theory accounts for an IAFM ground state if neither Ti nor Au have conventional local moments. X-ray photoemission spectroscopy (XPS) analysis suggests that Ti is close to the non-magnetic 4+ oxidation state (Supplementary Note 1). This is unexpected in light of the high magnetic volume fraction observed in the μSR measurements presented below, which, together with the single phase XPS and neutron patterns in Supplementary Figs 1 and 2, indicates that the observed magnetic behaviour is indeed intrinsic. Therefore, this suggests that Pmma TiAu is the first IAFM metal with no magnetic constituents, with the magnetic ground state strongly affected by spin fluctuations.
(a) Left axis: zero-field-cooled magnetic susceptibility as a function of temperature for μ0H=0.1 T applied field (1 e.m.u.=10 A cm−2). Right axis: inverse susceptibility H/M along with a Curie–Weiss-like fit (solid line), with θ≈−37 K (marked by a dashed line). (b) The crystal structure of TiAu with Ti (small) and Au (large) atoms, and the orthorhombic unit cell outlined in thin black lines. The arrows identify the crystallographic directions, marked by a, b and c axes.
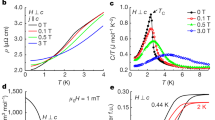
By contrast with most known weak itinerant (ferro- or antiferro-) magnets, the TiAu electrical resistivity (Fig. 2a) and specific heat data (Fig. 2b) also show signatures of the phase transition around 36 K. The H=0 ρ(T) data are typical of a good metal, decreasing nearly linearly from room temperature down to ∼40 K. A drop of about 10%, similar to the loss of spin-disorder scattering, occurs at TN (Fig. 2a). Although often the gap opening associated with the SDW ordering results in a resistivity increase, a similar drop was observed in BaFe2As2 single crystals12. In the absence of local moment ordering, the decrease in the resistivity at TN results from the balance of the loss of scattering due to Fermi surface nesting (see below) and the gap opening due to the SDW AFM state. At the same temperature in TiAu, a small peak becomes visible in the specific heat data Cp (Fig. 2b), such that TN in this AFM metal can be determined, as shown by Fisher13,14, from peaks in Cp (most visible in Cp/T), d(MT)dT and dρ/dT (Fig. 2c). Distinguishing between local and itinerant moment magnetism is inherently difficult, especially in the nearly unexplored realm of IAFMs. It is therefore surprising that in TiAu, the evidence points toward its itinerant magnetic moment character. The fact that the peak in Cp is not as strong as Fisher’s prediction13 is one such argument favouring the itinerant moment scenario in TiAu. Another argument is the small magnetic entropy Sm (grey area, Fig. 2c) associated with the transition (solid blue line, Fig. 2c). Even though the Sm calculated after assuming a polynomial non-magnetic Cp around the transition (dashed line, Fig. 2c) is an underestimate, it amounts to only 0.2 J mol−1 K−1 or ∼3% of Rln2.
H=0 temperature-dependent resistivity (a) and specific heat (b) with black arrows indicating the feature corresponding to TN. (c) The ordering temperature TN (vertical dotted line) for TiAu determined from peaks in the temperature derivatives of resistivity, dρ/dT (H=0, black triangles, left axis), and d(MT)/dT (μ0H=0.1 T, red squares, left axis), and in Cp/T (H=0, blue circles, right axis). The entropy Sm (solid blue line, right axis) is calculated by subtracting a polynomial non-magnetic component (dashed blue line) from the measured specific heat data (blue circles).
Despite the remarkably large paramagnetic moment μPM≅0.8 μB, derived from the Curie–Weiss-like fit of the inverse susceptibility (Fig. 1a, right axis), the field-dependent magnetization M(H) does not saturate up to μ0H=7 T, and the maximum measured magnetization is only 0.01 μB (Fig. 3). A closer look at the low temperature M(H) reveals a weak metamagnetic transition starting around μ0H=3.6 T for T=2 K (circles, Fig. 3). This is most apparent in the derivative dM/dH (open symbols) rather than in the as-measured isotherms (full symbols), with the latter nearly indistinguishable well below (T=2 K) and above (T=60 K) the magnetic ordering temperature. It has been shown by Sandeman et al.15, that, within the Stoner theory, the presence of a sharp double peak structure in the electronic density of states (DOS) sufficiently close to the Fermi level results in a metamagnetic transition. The argument requires that the paramagnetic Fermi level lie in between the two peaks of the DOS, and this is indeed revealed by the band structure calculations for TiAu, as is shown below. It results that, as the Fermi sea is polarized by the applied magnetic field H, the majority and minority spin Fermi levels feel the effect of the two DOS peaks at different values of induced magnetization. The DOS peak that is closest to the Fermi level will lead to a sharp increase (decrease) in the population of the majority (minority) spin band, resulting in a metamagnetic transition.
The magnetization isotherms M(H) (full symbols, left axis) and the derivative dM/dH (open symbols, right axis) for T=2 K (circles) and 60 K (triangles). No saturation is achieved for magnetic fields up to 7 T. A metamagnetic transition is observed around 4 T in the T=2 K isotherm, but not in the one above TN.
Evidence of Static magnetic order in the full volume
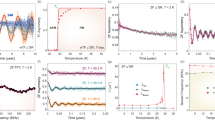
Muon spin relaxation data shown in Fig. 4 support the static magnetic order developing in the full volume fraction, with the transition temperature corresponding to the anomaly in the magnetic susceptibility, resistivity and specific heat shown in Fig. 2c. For temperatures above 35 K, the total asymmetry undergoes a negligibly small relaxation, signalling lack of static magnetic order (Fig. 4a). In the time spectra observed in zero field (ZF), a fast decaying front end begins to develop around 35 K, and becomes more pronounced for lower temperatures. This early time decay results from the build up of static internal field, since a small longitudinal field (LF), μ0H=0.01 T, eliminates this relaxation via the decoupling effect (Fig. 4b). The time spectra in ZF are fitted with the relaxation function G(t), expected for a Lorentzian distribution of local fields16:
(a) Time dependence of the asymmetry in H=0, fit with equation (1) (solid lines). (b) A small applied longitudinal field μ0H=0.01 T eliminates the relaxation response. For comparison, the H=0 T=2 K asymmetry is shown in black circles. (c) Relaxation rate a (black circles, left) and volume fraction (red circles, right) as a function temperature (H=0). (d) Integrated intensity of the (0, π/b, 0) TiAu magnetic Bragg peak as a function of temperature with mean-field fit (TN=36±2 K, black curve). Inset: net counts normalized for 2 min. counting time between 2.5 and 60 K, showing the (0, π/b, 0) magnetic peak fit with a resolution-limited Gaussian (red line). Uncertainties are statistical in origin and represent one standard deviation.

where f represents the volume fraction with static magnetic order. Detailed reasoning for the choice of this fitting function is given in the Supplementary Note 2. The temperature dependence of the relaxation rate a and the magnetic volume fraction f are shown in Fig. 4c. A reasonably sharp transition occurs below TN=36 K to a state with 100% ordered volume, preceded on cooling by a small temperature region around TN characterized by the finite volume fraction f, which suggests co-existence of ordered and paramagnetic volumes in real space via phase separation.
An important feature found in both ZF and LF time spectra is the absence of dynamic relaxation, expected for critical slowing down of spin fluctuations around TN. Such an effect should have resulted in the 1/T1 relaxation of the asymmetry measured in μ0H=0.01 T, since this LF can eliminate the effect of static magnetism, while dynamic effects survive in a small LF. The observed relaxation rate 1/T1 in LF=100 G was <0.02 μs−1. Using the well-known formula 1/T1∼Δ2τc, with the local field strength Δ=1 μs−1, we then find that the correlation time τc of the local field fluctuations should be <20 ns. Critical slowing down of spin fluctuations slower than this should have resulted in an observable decay in the LF spectra near the spin freezing temperature ∼36 K. Another piece of information comes from the absence of the decay of the 1/3 component in ZF and the decoupled time spectra in LF at low temperatures. These spectra indicate that the local field at low temperatures in the ordered state is quasi-static, with the time scale of 10 μs or more. See ref. 16 for more details.
Together with the ZF relaxation function (equation (1)) which solely involves static effects, the present data indicate complete absence of dynamic critical behaviour. Although occurring in a limited temperature region, the aforementioned phase separation indicates that the transition is likely first-order, without dynamic critical behaviour. As shown in Supplementary Table 1, similar absence of dynamic critical behaviour associated with phase separation was observed in μSR studies of the itinerant helimagnet MnSi in an applied pressure of 13–15 kbar17, near the pressure-tuned quantum crossover to the paramagnetic phase. Such tendencies were also seen in the itinerant ferromagnet (Sr,Ca)RuO3 close to the disappearance of static magnetic order around a Ca concentration of 0.7 (ref. 18). The first-order transition may be a generic feature of weak magnetic order in itinerant–electron systems19.
As Supplementary Table 2 shows, the magnitude of the internal magnetic field in TiAu in the ordered state is very small, compared with μSR results in other itinerant–electron systems, dilute alloy spin glasses or the incommensurate SDW system (Sr1.5Ca0.5)RuO4 (ref. 20). Although this indicates a very small ordered moment in TiAu, it is not possible to estimate the moment size since the hyperfine coupling constant could depend strongly on the assumption of the location of muon sites. The line shape of the ZF μSR data in equation (1) is obtained for the case of dilute alloy spin glasses where the local field at the muon site varies due to different distances to the moment site16. However, the same line shape was also observed in (Sr1.5Ca0.5)RuO4 in which incommensurate SDW order was recently confirmed by neutron scattering. Therefore, it is difficult to determine the spin structure of the TiAu system from the present μSR data alone. In general, the observation of long-lived oscillations by μSR can indicate homogenous long-range order, but the absence of oscillations does not rule out long-range magnetic correlations. This feature can be found in many cases of known AFM and FM systems, as reviewed in the Supplementary Note 2.
Evidence of Long-range antiferromagnetic order
Neutron diffraction measurements above (T=60 K) and below (T=2 K) the ordering temperature reveal a resolution-limited magnetic peak (inset, Fig. 4d, Supplementary Fig. 3) in the low temperature data. The temperature dependence of this peak indicates magnetic ordering at TN=36(2) K. The magnitude of the ordered moment is estimated to be 0.15 μB per Ti, consistent with a small itinerant moment. The neutron data eliminate the possibility that the observed magnetism is due to dilute magnetic impurities. The μSR results that show a magnetic phase fraction of 100% eliminate the possibility of neutron signal coming from a minority phase of small volume. These arguments suggest that the magnetism of the present system is an intrinsic feature of TiAu. Since it is not possible to determine the origin of the LSG line shape observed in μSR (see Supplementary Figs 4 and 5 and the discussion in Supplementary Note 2), the present work relies on neutron diffraction measurements to show long-range order, and μSR for information on volume fractions and absence of critical spin dynamics. More detailed and general discussions on limitations of μSR and neutron measurements, and the merits of the combination of the two methods, can be found in Supplementary Note 3, with the Supplementary Fig. 6 illustrating various spin patterns possible in real compounds, and Supplementary Fig. 7 showing possible neutron (a–f) and μSR (g–j) responses.
Band structure calculations
Even though the experimental evidence demonstrates long-range antiferromagnetic, small moment ordering in orthorhombic TiAu, a comparison between the experimental data with theoretical results from band structure calculations are of interest. These were performed using a full-potential DFT21 while taking spin–orbit coupling into account (see the Methods section for more details). A number of possible magnetic configurations were considered: ferromagnetic (FM), AFM SDW with modulation vectors Q1=(0, 2π/3b, 0) (AFM1) and Q2=(0, π/b, 0) (AFM2). Their energies relative to the paramagnetic state were estimated to be EFM=−35 MeV per Ti, EAFM1=−47 MeV per Ti and EAFM2=−34 MeV per Ti, respectively. Given the systematic error bars of the exchange-correlation potential employed in the DFT, the calculated energy values point to a AFM ground state with wavevector Qexp=(0, k, 0), with k between 2π/3b (AFM1) and π/b (AFM2), a value consistent with the neutron diffraction experiments. However the uncertainty in determining the exact wavevector from DFT does not affect the conclusions from the overwhelming experimental evidence for the itinerant AFM order in TiAu. Furthermore, the calculation yields a small ordered magnetic moment μcalc for all surveyed configurations, 0.52 μB per Ti≤μcalc≤0.74 μB per Ti, reflecting the itinerant nature of the ordered moment. This DFT overestimate compared to the experimental moment estimate of 0.15 μB per Ti from neutron scattering is likely a result of strong spin fluctuations which cannot be accounted for by the calculations. The same problem was also encountered in Fe pnictides, which are also itinerant SDW AFM compounds22,23. In the case of TiAu this may be remedied by future dynamical mean-field theory calculations, beyond the scope of this mainly experimental report of IAFM TiAu.
It is instructive to analyse the origin of magnetism in TiAu using the input from the band structure calculations. A picture that is often employed is that of the weak-coupling random phase approximation, resulting in the generalized Stoner criterion for the bare magnetic susceptibility χ(0) at a reciprocal wavevector Q24:

Within this picture, the idealized itinerant limit can be understood as the case where χ(Q) is strongly peaked at a particular Q vector, resulting in a SDW ordering at that wavevector. In this case, the Q dependence of the interaction strength I(Q) is unimportant. Traditionally, for instance in Cr25, the peak in χ(0)(Q) is understood as originating from Fermi surface nesting. Indeed, the calculated Fermi surface of the non-magnetic TiAu (Fig. 5c and Supplementary Fig. 8) exhibits large nearly nested regions in the kb direction with the nesting wavevector Qnest=(0, k, 0) discussed above. In one spatial dimension, nesting is known to result in a logarithmic divergence of the susceptibility at Qnest=2kF, χ(0)(Qnest)∼−ρ(EF)log[ρ(EF)T], resulting in the celebrated Peierls mechanism for charge density wave and SDW, with ρ(EF) representing the electronic density of states at the Fermi level. However in higher dimensions, it was pointed out that the divergence of χ(0) is strongly suppressed26, and moreover, the ordering wavevector Q of the charge density wave (and by analogy, SDW) does not generally coincide with the nesting wavevector Qnest27, shown to be the case in example, rare earth tritellurides26,27. The reason behind this is that the real part of the susceptibility χ(Q) contains the integration over all bands deep below the Fermi level, whereas nesting is the property of the Fermi surface itself and its effect is limited (except in the special case of perfect nesting, as is the case in one dimension).
(a) The non-magnetic density of states (thin black line) exhibits a peak close to the Fermi surface, similar to that seen in other itinerant magnets. (b) For the AFM1 ground state, the finite total density of states (thick red line) at the Fermi energy is flanked by two peaks around 0.1 eV, which explains the metamagnetic transition at low T (see text). (c) The electron spin density shows a modulation along the b axis, consistent with the k=2π/3b nesting shown in d. The colour scale indicates degree of electron polarization, ranging from spin-up (red) to spin-down (purple). The arrows identify the crystallographic directions, marked by a, b and c axes. Fermi surface with nesting vector Qcalc=(0,2π/3b,0) is shown in d. The Fermi surface is coloured for ease of viewing. The arrows identify the wavevectors in the reciprocal space, marked by ka, kb and kc.
It is a non-trivial task to calculate χ(0)(Q) accurately from the DFT results, however the fact that all three magnetic configurations considered above have comparable energies indicates that χ(0)(Q) is not a simple single-peaked function. This goes to show that, while magnetism in TiAu is close to the itinerant limit, its mechanism is more complicated than in Cr25. The difference between Cr and TiAu is further highlighted by the fact that the latter has a considerably larger drop in the relative magnetic susceptibility ΔM/M at TN, where  . In TiAu, ΔM/M is ∼20%, nearly five times larger than in Cr25. In the latter, the small magnetization decrease at TN had been attributed to the small spin susceptibility (and not the larger orbital component) being affected by the gap associated with the SDW transition. Conversely, the larger magnetization change in TiAu might indicate a sizable effect on the orbital magnetization, as the SDW transition is now associated with more two dimensional nesting than that in Cr.
. In TiAu, ΔM/M is ∼20%, nearly five times larger than in Cr25. In the latter, the small magnetization decrease at TN had been attributed to the small spin susceptibility (and not the larger orbital component) being affected by the gap associated with the SDW transition. Conversely, the larger magnetization change in TiAu might indicate a sizable effect on the orbital magnetization, as the SDW transition is now associated with more two dimensional nesting than that in Cr.
Discussion
We evidence that orthorhombic TiAu is an IAFM without local moments and analogous to the only two IFMs with no magnetic elements, Sc3In and ZrZn2. Experimental evidence for the itinerant character of the magnetic state in TiAu includes small magnetic moment in the ordered state compared to the paramagnetic moment, as well as small magnetic entropy at TN. It is readily apparent that strong spin fluctuations are at play in this magnetic system. The exact role of the spin fluctuations, their strength, as well as the details of the magnetic structure in the ordered state, remain to be fully elucidated with further experiments. Additionally, doping experiments are underway, indicating that the magnetic order in doped TiAu is suppressed to 0 in a quantum critical regime with strong spin fluctuations. More detailed calculations using dynamical mean-field theory, left to a future in-depth theoretical study on the IAFM. Ultimately, the search for IAFMs appears to be a promising avenue for furthering our understanding of the complex magnetism, and providing the unifying picture for local and itinerant moment magnetism.
Methods
Sample preparation and composition analysis
Polycrystalline samples of TiAu were prepared by arcmelting, with mass losses no more than 0.3%. The hardness of the arcmelted samples rendered powder X-ray diffraction experiments difficult, and therefore X-ray diffraction data were collected at room temperature off the cross-section (about 3 mm in diameter) of cut and polished specimens using a custom 4-circle Huber diffractometer with graphite monochromator and analyser in non-dispersive geometry, coupled to a Rigaku rotating anode source producing CuKα radiation. X-ray photoemission spectroscopy was performed on the polished surface of the TiAu sample, using an XPS Phi Quantera spectrometer with a monochromatic Al X-ray source and Ar ion sputtering gun, used to cleanse the surface of contaminants. The alignment was checked by comparing the binding energy of the C1s peak to the published one28. More details can be found in the Supplementary Note 1. Heat treatment (annealing) at several different temperatures resulted in no measurable changes in either the structural or physical properties.
Magnetization, specific heat and resistivity measurements
The d.c. magnetization was measured in a Quantum Design (QD) Magnetic Property Measurement System from 2 to 400 K. At temperatures above 400 K, the magnetization data were collected using the Vibrating Sample Magnetometer option of a QD Physical Property Measurement System (PPMS) equipped with an oven. Specific heat using an adiabatic relaxation method, and four-probe d.c. resistivity measurements from 2 to 300 K were carried out in the QD PPMS environment.
μSR measurements
ZF and LF (up to μ0H=0.01 T) μSR measurements were performed at the M20 channel of TRIUMF, Vancouver, Canada. The cut TiAu samples of thickness around 0.1 cm and area of about 3.5 cm2 were mounted on a silver foil and oriented perpendicular to the direction of the incoming muons. For all experiments the beam momentum was ∼28 MeV c−1, with muons polarized along the flight direction.
Neutron diffraction measurements
Neutron diffraction data were collected on the BT-1 powder diffractometer and BT-7 thermal triple-axis spectrometer at the NIST Center for Neutron Research. For the neutron diffraction measurements the sample was sealed with helium exchange gas and mounted in a closed cycle refrigerator with a base temperature of 2.5 K. To search for magnetic scattering the high intensity/coarse resolution BT-7 spectrometer was employed in two-axis mode, with a fixed initial neutron energy of 14.7 MeV (λ=2.369 Å) and collimator (full-width-half-maximum) configuration open—PG(002) monochromator—80′—sample—80′ radial-collimator—position-sensitive detector29. Supplementary Fig. 3 shows the observed counts (full circles) for the magnetic peak. The solid curve is a fit to Gaussian (instrumental) peaks (solid curve). To characterize the sample and search for possible structural changes associated with the magnetic phase transition the BT-1 high resolution powder diffractometer was used. Collimators of 15′, 20′ and 7′ were used before and after the Cu (311) monochromator (λ=1.5401 Å) and after the sample, respectively, and data were collected in steps of 0.05° in the 2θ range of 3–168°. BT-1 data were used for the crystallographic analysis at T=5 K (black) as shown in Supplementary Fig. 2, with all peaks identified as the orthorhombic Pmma TiAu phase (vertical marks). The results of Rietveld structural refinements with the General Structure Analysis System software of the data below (T=5 K) and above (T=60 K) TN as well as those obtained from room temperature X-ray diffraction are summarized in Supplementary Table 1.
Theoretical calculations
Band structure calculations were performed using the full-potential linearized augmented plane-wave method implemented in the WIEN2K package30. The PBE-GGA was used as the exchange potential, the default generalized gradient approximation for the exchange-correlation potential in WIEN2K31 and spin–orbit coupling was included in a second-variational fashion32. The lattice parameters and atomic positions were determined from both neutron and X-ray diffraction and are reported in the Supplementary Table 1. A 10 × 10 × 10 k-point grid was used, and shift away from high symmetry directions was allowed. The convergence criterion for force is 1 mRyd per a.u. (1 Ryd=13.6 eV), with the residual force for the Q=(0, 2b/3π, 0) state less than 3.5 mRyd per a.u. (or 90 MeV Å−1). For the density of states plot, the Gaussian broadening was used, with a broadening factor of 3 mRyd. In order to make the Fermi surface plot (shown in Fig. 5c) easier to read, a separated Fermi surface plot for the different bands in shown in Supplementary Fig. 8.
Additional information
How to cite this article: Svanidze, E. et al. An itinerant antiferromagnetic metal without magnetic constituents. Nat. Commun. 6:7701 doi: 10.1038/ncomms8701 (2015).
References
Heisenberg, W. Zur theorie des ferromagnetismus. Z. Physik 49, 619–636 (1928).
Stoner, E. C. Collective electron ferromagnetism. P. R. Soc. Lond. A 165, 372–414 (1938).
Moriya, T. & Kawabata, A. Effect of spin fluctuations on itinerant electron ferromagnetism. J. Phys. Soc. Jpn. 34, 639–651 (1973).
Moriya, T. & Kawabata, A. Effect of spin fluctuations on itinerant electron ferromagnetism II. J. Phys. Soc. Jpn. 35, 669–676 (1973).
Moriya, T. & Takahashi, Y. Itinerant electron magnetism. Annu. Rev. Mater. Sci. 14, 49–66 (1984).
Matthias, B. T., Clogston, A. M., Williams, H. J., Corenzwit, E. & Sherwood, R. C. Ferromagnetism in solid solutions of Scandium and Indium. Phys. Rev. Lett. 7, 7–9 (1961).
Matthias, B. T. & Bozorth, R. M. Ferromagnetism of a Zirconium-Zinc compound. Phys. Rev. 109, 604–605 (1958).
Donkersloot, H. C. & van Vucht, J. H. N. Martensic transformations in gold-titanium, palladium-titanium and platinum-titanium alloys near the equiatomic composition. J. Less-Common Met. 20, 83–92 (1970).
Schubert, K., Meissner, H. G., Poetzschke, M., Rossteutscher, W. & Stolz, E. Einige strukturdaten metallischer phasen (VII). Naturwissenschaften 49, 57 (1962).
Moriya, T. Spin Fluctuations in Itinerant Electron Magnetism Springer (1985).
Hasegawa, H. & Moriya, T. Effect of spin fluctuations on itinerant electron antiferromagnetism. J. Phys. Soc. Jpn. 36, 1542–1553 (1974).
Wang, X. F. et al. Anisotropy in the electrical resistivity and susceptibility of superconducting BaFe2As2 single crystals. Phys. Rev. Lett. 102, 117005 (2009).
Fisher, M. E. Relation between the specific heat and susceptibility of an antiferromagnet. Philos. Mag. 7, 1731–1743 (1962).
Fisher, M. E. & Langer, J. S. Resistive anomalies at magnetic critical points. Phys. Rev. Lett. 20, 665–668 (1968).
Sandeman, K., Lonzarich, G. & Schofield, A. Ferromagnetic superconductivity driven by changing Fermi surface topology. Phys. Rev. Lett. 90, 167005 (2003).
Uemura, Y. J., Yamazaki, T., Harshman, D. R., Senba, M. & Ansaldo, E. J. Muon-spin relaxation in AuFe and CuMn spin glasses. Phys. Rev. B 31, 546–563 (1985).
Uemura, Y. J. et al. Phase separation and suppression of critical dynamics at quantum transitions of itinerant magnets: MnSi and (Sr1−xCax)RuO3 . Nat. Phys. 3, 29–35 (2007).
Gat-Malureanu, I. M. et al. Muon spin relaxation and susceptibility measurements of an itinerant-electron system Sr1−xCaxRuO3: quantum evolution from ferromagnet to paramagnet. Phys. Rev. B 84, 224415 (2011).
Belitz, D. & Kirkpatrick, T. R. First order transitions and multicritical points in weak itinerant ferromagnets. Phys. Rev. Lett. 82, 4707–4710 (1999).
Carlo, J. P. et al. New magnetic phase diagram of (Sr, Ca)2RuO4 . Nat. Mater. 11, 323–328 (2012).
Martin, R. M. Electronic Structure: Basic Theory and Practical Methods Cambridge University Press (2008).
de la Cruz, C. et al. Magnetic order close to superconductivity in the iron-based layered LaO1−xFxFeAs systems. Nature 453, 899–902 (2008).
Ma, F., Lu, Z. & Xiang, T. Arsenic-bridged antiferromagnetic superexchange interactions in LaFeAsO. Phys. Rev. B 78, 224517 (2008).
Kübler, J. Theory of Itinerant Electron Magnetism Oxford University Press (2009).
Fawcett, E. Spin-density-wave antiferromagnetism in chromium. Rev. Mod. Phys. 60, 209–283 (1988).
Yao, H., Robertson, J. A., Kim, E. A. & Kivelson, S. A. Theory of stripes in quasi two dimensional rare-earth tritellurides. Phys. Rev. B 74, 245126 (2006).
Johannes, M. D. & Mazin, I. I. Fermi surface nesting and the origin of charge density waves in metals. Phys. Rev. B 77, 165135 (2008).
NIST X-ray Photoelectron Spectroscopy Database (National Institute of Standards and Technology, 2012) http://srdata.nist.gov/xps/.
Lynn, J. W. et al. Double focusing thermal triple axis spectrometer at the NCNR. J. Res. NIST 117, 61–79 (2012).
Blaha, P., Schwarz, K., Madsen, G. K. H., Kvasnicka, D. & Luitz, J. WIEN2k: an augmented plane wave + local orbitals program for calculating crystal properties (Techn. Universität Wien, 2001) http://www.wien2k.at .
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Singh, J. J. Planewaves, Pseudopotentials and the LAPW Method Kluwer Academic Publishers (1994).
Acknowledgements
We would like to thank M.B. Maple, P. Dai, M. Foster, S. Kivelson, Z. Deng, T. Munsie, T. Medina, and G. Luke for assistance and discussions. The work at Rice University was supported by NSF DMR 0847681 (E.M. and E.S.), AFOSR MURI (J.K.W.) and the Welch Foundation grant C-1818 (A.H.N.). Work at Brookhaven National Laboratory (M.B.G. and M.C.A.) was carried out under the auspices of the US Department of Energy, Office of Basic Energy Sciences, under Contract No. DE-AC02-98CH1886. T.B. and T.S. are supported by the U.S. Department of Energy, Office of Basic Energy Sciences, Materials Sciences and Engineering Division, under Award #DE-SC0008832. A portion of this work was performed at the National High Magnetic Field Laboratory, which is supported by National Science Foundation Cooperative Agreement No. DMR-1157490 and the State of Florida. Work at Columbia and TRIUMF (L.L., B.F. and Y.J.U.) is supported by NSF grants DMR-1105961, OISE-0968226 (PIRE) and DMR-1436095 (DMREF), REIMEI project from JAEA, Japan, and the Friends of Todai Inc. Foundation. The identification of any commercial product or trade name does not imply endorsement or recommendation by the National Institute of Standards and Technology.
Author information
Authors and Affiliations
Contributions
E.M. designed the study, E.S. prepared the samples, performed susceptibility, specific heat, resistivity and X-ray photoemission spectroscopy measurements. E.M and E.S. performed the data analysis and wrote the manuscript with contributions from all authors. J.K.W. and A.N. performed band structure calculations and analysis. T.B. and T.S. were responsible for X-ray measurements and structural characterization. L.L., B.F. and Y.J.U. performed muon spin relaxation measurements and data analysis, M.B.G. and M.C.A. measured the high-temperature magnetization, J.W.L. and Q.H. carried out neutron diffraction experiments and analysis.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-8, Supplementary Tables 1-2, Supplementary Notes 1-3 and Supplementary References (PDF 626 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Svanidze, E., Wang, J., Besara, T. et al. An itinerant antiferromagnetic metal without magnetic constituents. Nat Commun 6, 7701 (2015). https://doi.org/10.1038/ncomms8701
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms8701
This article is cited by
-
Synthesis of goldene comprising single-atom layer gold
Nature Synthesis (2024)
-
Field-induced quantum critical point in the itinerant antiferromagnet Ti3Cu4
Communications Physics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.