Purely hydrodynamic ordering of rotating disks at a finite Reynolds number

Abstract

Self-organization of moving objects in hydrodynamic environments has recently attracted considerable attention in connection to natural phenomena and living systems. However, the underlying physical mechanism is much less clear due to the intrinsically nonequilibrium nature, compared with self-organization of thermal systems. Hydrodynamic interactions are believed to play a crucial role in such phenomena. To elucidate the fundamental physical nature of many-body hydrodynamic interactions at a finite Reynolds number, here we study a system of co-rotating hard disks in a two-dimensional viscous fluid at zero temperature. Despite the absence of thermal noise, this system exhibits rich phase behaviours, including a fluid state with diffusive dynamics, a cluster state, a hexatic state, a glassy state, a plastic crystal state and phase demixing. We reveal that these behaviours are induced by the off-axis and many-body nature of nonlinear hydrodynamic interactions and the finite time required for propagating the interactions by momentum diffusion.

Introduction

Self-organization is the autonomous organization of components into patterns or structures and the underlying mechanism can be grouped into two classes: thermal and athermal origin^1,2. Compared with the understanding of self-assembly of a thermal system, which can be explained in terms of the free energy, that of an athermal system is far behind due to the lack of a firm theoretical background. Typical examples for the latter is active matter in hydrodynamic environments, which shows many interesting unconventional pattern formation with exotic dynamical features^{1,3,4,5,6,7,8,9,10,11}. Directional swimmers undergoing translational motion, like fishes, tend to swim together while forming a cluster of particular shape^6,7,9. The hexatic ordering of directionally self-propelling particles was also recently studied¹².

Rotation is another important type of motion. Self-organization of passive rotors was first observed in laboratory experiments by Grzybowski, Stone and Whitesides⁴. Such rotation can be induced by applying a torque to a particle by magnetic^4,13,14 and optical fields¹⁵. Self-organization of active rotors has also been studied intensively. For example, it was found that there are interesting stable bound states of spinning Volvox algae⁸. Furthermore, it was shown¹⁶ that microorganisms, like spermatozoa, self-organize into dynamic vortices and they form an array with local hexagonal order. This study indicates that large-scale coordination of cells can be regulated hydrodynamically, and chemical signals are not required. It was also shown recently that self-assembly of rotors is a generic feature of aggregating swimmers¹⁷. There has also been a theoretical prediction for intriguing self-organization of rotating molecular motors in membranes¹⁸. This and related problems have also been investigated by numerical simulations^{11,19,20,21,22,23,24}.

As described above, there exist two types of rotors²⁵: rotors driven by external torques are called passive rotors, while those that are internally driven are called active rotors and many such examples can be seen in biological systems. A realistic realization of a truly active system of self-rotors in biological systems may be one in which the particles are torque dipole with no resultant net torque on the system^18,21,25. To elucidate the physics of self-organization of flow created by rotors at a finite Reynolds number, a system of hard disks each of which is rotated by an externally applied torque is an ideal model system. Ordering of this system may be regarded as a nonequilibrium counterpart of thermodaynamic ordering of hard disks. We note that, unlike a thermodynamic system, where a state is selected solely by free energy, dynamic factors such as hydrodynamic interactions also affect the selection of a state of an out-of-equilibrium system.

For example, it has been now recognized that nonlinear hydrodynamic interactions play crucial roles in self-organization of rotating disks^4,13,14. In other words, the phenomena are beyond Stokes approximations, and may even have a link to self-organization of vortices²⁶, which is observed at a high Reynolds number. Vortex crystals are very interesting examples^27,28. The nonequilibrium, nonlinear, nonlocal, non-instantaneous nature of hydrodynamic interactions makes analytical approaches to this problem very difficult and thus numerical simulations are expected to play a crucial role. This problem also has a link to self-organization of a point vortex system^29,30, but the finite size and solidity of disks lead to far more rich behaviour. Here we employ a fluid particle dynamics (FPD) method³¹, which we developed for studying hydrodynamic interactions between colloidal particles (Methods). This method treats a solid colloid as an undeformable fluid particle inside which the viscosity is considerably higher than the surrounding liquid. This approximation makes us free from solid–fluid boundary conditions, which significantly simplifies the computation. This method can quite naturally deal with many-body hydrodynamic interactions even at a high Reynolds number.

In this Article, we study self-organization of rotating hard disks in a two-dimensional (2D) incompressible liquid by using the FPD method. Like the Ising model for magnetic ordering or the hard sphere system for crystallization, this system may serve as a fundamental model system for studying dynamical phase behaviour caused by hydrodynamic interactions between rotating particles. The situation is similar to the above-mentioned experimental and theoretical works^4,13,14. We make our simulation in 2D to compare with the behaviour of its thermal counterpart, 2D hard disks, whose thermodynamic behaviour is reasonably understood³². Here we report surprisingly rich phase-ordering behaviours, such as aggregation, re-entrant order–disorder transition, glass transition, plastic crystal formation and phase demixing in this class of strongly nonequilibrium systems.

Results

Behaviours of a single and a pair of rotating disks

Before discussing many-body interactions between disks rotating with an angular frequency Ω, first we describe the behaviour of a dilute limit: behaviours of a single rotating disk and a pair of rotating disks (Supplementary Fig. 1; Supplementary Note 1). We characterize the rotation speed of a disk either by the angular frequency Ω or the relevant Reynolds number Re=ρa²Ω/η_ℓ (ρ: density; a: particle radius: η_ℓ: liquid viscosity). Figure 1a,b shows the 2D flow field around a rotating disk and the velocity distribution, respectively. The latter shows that the rotating velocity linearly increases with the distance from the centre of mass, r, inside a disk and decays as 1/r in its outside. This is the characteristic of the so-called Rankin vortex, that is, a forced vortex in the central core surrounded by a free vortex. We note that the Rankin vortex is known to mimic the 2D flow field of tornado and hurricane³³. For two co-rotating ‘point’ vortexes, the analytical solution is known and the two particles rotate around their centre of mass towards the same direction as the rotating direction^29,30. In this case, the radius of rotation is the half of the initial interparticle distance. For particles with a finite size, on the other hand, the direction of rotation and the rotation centre are the same as the case of point particles, but the radius of the rotation decreases with an increase in the rotation speed of the particles Ω, or Re. This problem has a similarity to viscous interactions of co-rotating vortices^29,34, but the crucial difference arises from the fact that the vortex core is an undeformable solid and not a liquid in our case. There are a few studies on spinning particles in 3D^25,35 however, we note that there is an essential difference between 2D and 3D problems (Supplementary Fig. 2; Supplementary Note 2). We confirm that if we fix the centres of mass of two rotating particles on a fixed line they always repel each other by the Magnus force^4,13,36. The attraction between particles is thus due to interparticle hydrodynamic interactions, as schematically explained in Fig. 1c. The flow field generated by a rotating disk makes the other disk follow it, and vice versa. Thus, two particles try to follow each other while rotating around the centre of mass of the pair. In 3D, on the other hand, such hydrodynamic interactions weaken due to the presence of the escape dimension, thus the Magnus force wins over the hydrodynamic attractive force, and particles repel each other. In 2D, this hydrodynamic attraction overwhelms the repulsion due to the Magnus force, which leads to the rotating pair of particles (Fig. 1d), whose interparticle distance monotonically decreases with an increase in Ω, or Re (Fig. 1e), as long as the area fraction of disks, Φ, is sufficiently small. In relation to the above dimensionality effect on hydrodynamic interactions between rotors, it is worth noting that the hexagonal ordering observed by Grzybowski et al.^1,4,13,14 at finite Reynolds numbers is due to the effective hydrodynamic repulsion between the disks floating at an interface in 3D (that is, 2.5D).

Figure 1: Behaviours of an isolated rotating disk and co-rotating disks in a dilute suspension.

(a) 2D flow fields around an isolated rotating disk. (b) The velocity profile as a function of r/a. ε/(aω) increases linearly with r inside the disk and then decays as 1/r in its outside, which is the characteristic of the so-called Rankin voltex. (c) Schematic picture of a pair of two disks rotating around the centre of mass. The two disks are rotating anticlockwise with the same speed. (d) Trajectory of coupled rotating particles (the system size=256 × 256 lattices). The initial separation of the particles (arrowed) was 30 lattices and each particle rotates anticlockwise with Re=0.76. (e) Temporal change in the interparticle separation. We note that for all the cases including Re=0.7 the interparticle distance eventually reaches a final steady-state value of the separation (see d), which monotonically decreases with Re. (f) A cluster of disks formed at Φ=0.04 at Re=5.94. We confirm that irrespective of the value of Re a cluster is always formed in the range of Re studied.

Structural ordering due to many-body hydrodynamic interactions

Now we consider the dynamical behaviour of a system of many disks rotating in the anticlockwise direction with Ω. The hydrodynamic attraction between rotating disks leads to the formation of rotating clusters for low Φ (Fig. 1f). The higher rotation speed of individual disks leads to the formation of a more compact rotating cluster. This tendency is basically the same as that for a pair of rotors (Fig. 1e). For this regime, only one cluster is formed in the simulation box and the whole cluster rotates in the anticlockwise direction, as shown in Fig. 1f. A cluster always tends to have a circular shape, but it does not have any particular internal structural order, partly because imperfect matching between the size and the number of particles leads to structural fluctuations: the internal structure is basically controlled by the number of disks in it and Re, which determine the cluster size, but fluctuating with time. With a further increase in Re, however, this cluster state becomes unstable, since the repulsive Magnus force of nonlinear origin eventually wins over the hydrodynamic attraction for high Re (see below). Above a critical Φ (Φ_c~0.05), on the other hand, a system exhibits a re-entrant transition between states as a function of Ω (Fig. 2a): for low Ω, a system is in a disordered liquid state with large fluctuations, but with an increase in Ω it enters into a rather stable hexatic phase where rotating particles are localized on a hexagonal lattice. The border between the cluster to the hexatic state is rather sharp as a function of Φ.

Figure 2: Re-entrant state transitions observed at a rather high Φ.

(a) Snapshots of particle configurations together with the velocity fields. The system size is 256 × 256 lattices, the number of particles is 80 and Φ~0.157. We can see sequential transitions from disordered, hexatic ordered to disordered states with an increase in Re. (b) Upper panel: the direction of the hydrodynamic force θ measured from the interparticle axis. Lower panels: patterns formed by Brownian simulations for the two off-axis forces: left is a liquid state for θ=89°, whereas the right panel is a hexatic state for θ=85°. (c) Re-dependence of the hexatic order parameter Ψ₆, which clearly shows the re-entrant behaviour for various Φ’s (expressed in %). (d) The degree of fluctuations of Ψ₆ as a function of Re for various Φ’s (expressed in %). We can see that, as in a thermodynamic hexatic-ordering transition, the order parameter exhibits large amplitude fluctuations near the transition points. (e) Re-dependence of the decay of the spatial correlation function of the hexatic order parameter g₆(r) normalized by the radial distribution function g(r) around the transition at low Re for Φ=0.157. In the hexatic state, g₆(r)/g(r) decays with a power law with the exponent of −1/4, as it should be³². In the disordered states, it decays almost exponentially. (f) The same as e, but for around the transition at high Re. In the hexatic state, g₆(r)/g(r) again decays with a power law with the exponent of −1/4. In the disordered states, it decays almost exponentially.

The transition can be characterized by the nature of interparticle interactions. Here we analyse a point pattern to extract the nature of interparticle interactions. The point pattern analysis is very useful to determine the overall interparticle interactions³⁷. Here we use what we call N function, which is the number of connected regions as a function of the radius of circle whose centre is located at the centre of each disk. The number of connected regions decreases monotonically, with an increase in the circle radius, from the total number of disks N₀ to 1. Here we use N for the one normalized by N₀. By comparing N for a reference system made of randomly distributed disks, that is, Poisson pattern, we can judge whether the interaction is repulsive or attractive. For a system of particles with repulsive interactions, particles form a rather regular pattern and N decays slower than that for the corresponding Poisson pattern. For a system of particles with attractive interactions, on the other hand, particles form a cluster pattern and N decays faster than that for the corresponding Poisson pattern. In Fig. 3a, we show the N function for Φ=0.04. We can clearly see that for the cluster-forming case at Re=0.72 the interaction is attractive, whereas for the disordered state at Re=5.97 the interaction is repulsive. In Fig. 3b, we show the N function for Φ=0.15. We can see that for all the value of Re the interaction is basically repulsive, but its strength is maximum at Re=5.9, for which the hexatic order is formed.

Figure 3: The analysis of point patterns.

(a) The decrease in N as a function of the particle radius a/ρ^1/2 for Φ=0.04, where ρ is the particle number density and ρ^−1/2 is the average interparticle distance. (b) The decrease in N as a function of the particle radius a/ρ^1/2 for Φ=0.15.

The transition can be seen even more clearly by the degree of localization of the flow field: for a hexatic state, each particle has its own localized rotational flow field, whereas for a cluster state a single vortex is always formed and thus the flow field is strongly delocalized. However, the precise nature of the cluster-hexatic phase transition, such as whether the transition is continuous or discontinuous and whether a disorder state always exists between the two states or there exists a critical point between the cluster and the hexatic state, is not clear at this moment. To access this problem, we need to survey the border region of a bigger system size with a high resolution of Φ and Re. Although this is a very interesting problem, we leave this for future investigation.

We also find that the hexatic state is eventually destabilized and melts by a further increase in Ω and the system becomes disordered again. We note that for all these states interparticle interactions are basically repulsive, unlike the case of low Φ. Although the torque exerted to each disk is exactly the same, the rotation speed of a disk can in principle depend on the particle configuration around it. Here we show in Fig. 4 the normalized variance of the angular frequency Ω of rotating disks as a function of the averaged Ω. For ordered states, the variance, that is, the fluctuations of rotation speed, becomes very small, indicating all the disks rotating with almost the same frequency. For disordered states, on the other hand, the variance is large, reflecting the large fluctuations of particle environment. This result indicates a strong negative correlation between the degree of fluctuations of rotational speed of particles and the degree of order.

Figure 4: The normalized variance of the angular frequency Ω of rotating disks as a function of the averaged Ω for Φ=0.15.

We can see the negative correlation between the degree of the hexatic order and the variance.

In Fig. 2c, we show the Ω-dependence of the hexatic order parameter Ψ₆, which clearly indicates the re-entrant nature of the state transitions. The transitions can also be characterized by the magnitude of fluctuations of Ψ₆, or the susceptibility (see Fig. 2d), which is also observed in a thermodynamic hexatic ordering in 2D disks. In the hexatic ordered state, we confirm the power law decay of the spatial correlation of the hexatic order that is specific to the hexatic phase (see Fig. 2e,f). We do not see any indication of the positional order since the radial distribution function decays almost exponentially (see below).

Here we show a hexatic phase observed in a large system (the system size=2,048² lattices and the number of particles=5,120) at Φ=0.15 and Re=5.9. We can see grain boundaries between hexatic order with different orientations as shown in Fig. 5a,b. Figure 6a,b shows the decay of the correlation function of the hexatic order normalized by the radial distribution function g(r), g₆(r)/g(r), and that of g(r)−1, respectively. We can see that g₆(r)/g(r) decays algebraically for a short distance r<400, but decays faster for long distance. This is because the size of monodomain regions is finite (see Fig. 5a,b). On the other hand, we can see that g(r) decays faster than an algebraic decay even for r<400, where g₆(r)/g(r) decays algebraically. This clearly indicates the absence of quasi-long-range translational order in the ordered phase. Thus, we conclude that the ordered phase is the hexatic phase. The appearance of the transitions between dynamical states as a function of Φ and Ω in athermal systems is quite striking, which is reminiscent of phase transitions in a thermal system. We stress that the interparticle interaction in our system is of purely hydrodynamic origin.

Figure 5: Hexatic ordering in a large system.

Here we show results of large-size simulation (the system size=2,048² lattices and the number of particles=5,120). The area fraction Φ=0.15 and Re=5.9. (a) The structure of a hexatic state shown with three colours (yellow for particles with six neighbours; red for particles with more than 7 neighbours; blue for particles with less than 5 neighbours). (b) The same as a, but with orientations of hexatic order. See the colour bar for the meaning of colour.

Figure 6: Spatial correlation of hexatic and positional order.

(a) The spatial decay of the correlation function of the hexatic order g₆(r) in Fig. 5a normalized by the radial distribution function g(r). We can see that it decays algebraically in a short distance, but decays faster for long distance because of the finiteness of the domain size. The dashed line has a slope of −1/4. (d) The spatial decay of the radial distribution function g(r) for the pattern shown in Fig. 5a. It decays more quickly than the decay of g₆(r) even for rather short distance (r<400). The dashed line has a slope of −1/3.

Here we consider a quite interesting feature of hydrodynamic interparticle interactions, which are absent in a thermal system. Binary interaction potentials that lead to phase ordering in thermal systems always act along the interparticle axis, that is, along the line connecting the centres of mass of two interacting particles. However, this is not the case for our athermal system. The nonlinear Magnus force acts along the line connecting two particles, whereas the Stokes force acts according to the flow direction. Furthermore, linear hydrodynamic interactions are tensorial and act not along the interparticle direction. Thus, the total hydrodynamic force does not act along the interparticle axis. The direction of the hydrodynamic force as a function of Re is shown in the upper panel of Fig. 2b with a schematic explanation. With an increase in Re, both the Magnus and the hydrodynamic force increase. However, the nonlinear Magnus force increases more rapidly than the linear hydrodynamic force. Thus, the direction of the total force, which is repulsive, approaches the interparticle axis. A strong enough repulsive force acting on particles not so far from the interparticle direction leads to the formation of hexatic order. To verify this scenario, we have performed Brownian dynamics simulation (without hydrodynamic interactions) by changing the angle θ between the direction of an artificial repulsive force and the interparticle direction. We find that when θ is continuously decreased a system indeed forms hexatic order below a critical value of θ (see the lower panels of Fig. 2b).

Next we discuss the nature of the translational motion of rotating disks in the disordered states. To see this, we calculate the mean-square displacement of disks ‹Δr²(t)› (see Fig. 7a). Interestingly, in the two types of disordered states, particle motion is apparently diffusional: in the long-time limit, we observe the relation ‹Δr²(t)›~D_efft, where D_eff is the effective diffusion constant and t is the time duration. It should be noted that in our system there is no thermal noise and an isolated rotating disk exhibits no motion. For a pair of rotating particles, we also observe that their trajectory is very stable and there is no fluctuation (see Fig. 1d). Thus, the apparently diffusional motion should be the consequence of self-generated force noise due to many-body hydrodynamic interactions of both linear and nonlinear origin. We can also see no diffusion, or non-ergodic behaviour, for the hexatic state. The random nature of fluctuations may be related to the long-range nature of hydrodynamic interactions, which makes a number of surrounding particles affecting a particle large enough to provide strong stochastic spatio-temporal fluctuations.

Figure 7: Dynamical behaviour and state diagram of rotating disks.

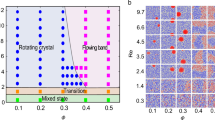
(a) The mean-square displacement ‹Δr²›^1/2 versus time t. Despite the absence of thermal noise, particles undergo Brownian-like diffusive motion ‹Δr²›^1/2=D_efft with an effective diffusion constant D_eff in the long-time limit. The black dashed line is the momentum diffusion constant, or the kinematic viscosity ν(=η_ℓ/ρ). (b) Re-dependence of the effective diffusion constant D_eff. In the hexatic ordered state, D_eff is very low and there is no diffusive behaviour, as it should be (see a). At high Re, D_eff exceeds ν (indicated by the blue horizontal line), which means that fluctuations of particles cannot be suppressed by hydrodynamic interactions at high Re (see text). (c) State diagram on the Re–Φ plane. At low Φ and low Re, the system forms a cluster due to hydrodynamic attractive interactions. At high Φ, on the other hand, the system exhibits re-entrant transition between a disordered chaotic liquid state and ordered hexatic state. The latter state is basically stabilized by the repulsive interaction due to the Magnus effect.

For high Re, the particle diffusion starts to become comparable or faster than momentum diffusion: D_eff≥ν, where ν is the momentum diffusion constant or the kinematic viscosity ν=η_ℓ/ρ (see Fig. 7a,b). This implies that hydrodynamic interactions induced by the rotation of a particle cannot fully propagate to its neighbouring particles for high Re. This weakens the repulsive interactions of particles and eventually leads to the melting of the hexatic state. Thus, the re-entrant hexatic ordering as a function of Re may be explained as follows: the increase in the Magnus force of nonlinear origin with an increase in Re makes the direction of the interparticle force more aligned along the interparticle direction and also increases the strength of the repulsive force. This leads to stabilization of the hexatic order, as explained above. The ordered state is stable until the repulsive interaction is weakened by the intrinsically kinetic nature of hydrodynamic interactions: Unlike ordinary interparticle interactions that propagate with the speed of light, hydrodynamic interactions propagate much slower in a diffusive manner with the momentum diffusion constant ν. This kinetic weakening of the repulsive force eventually destabilizes the hexatic state and leads to melting into the disordered chaotic state.

Here we summarize what we observed in our system and show the state diagram as a function of Φ and Re (see Fig. 7c). We can see the three states, that is, disordered fluid, cluster and the ordered hexatic state. It is quite striking that particles interacting by hydrodynamic interactions alone exhibit such rich phase behaviours.

Other interesting states formed by rotating disks

Finally, we show other interesting states formed by rotating particles. The introduction of size polydispersity to hard spheres is known to lead to the formation of a glass state for a thermal system³⁸. Motivated by this, we introduce the polydispersity in the rotating speed of particles, whose variance is δ, and indeed find a non-ergodic glassy state of the rotating particles (Fig. 8a) for high enough δ (Fig. 8b): liquid–glass transition in an athermal system. Reflecting the nearly continuous nature of the liquid-to-hexatic transition^32,39, there is no sharp transition from a hexatic to a disordered glassy state. Although disks are rotating around their centres of mass, their positions are frozen in a disordered configuration and thus the system can be regarded as a non-ergodic glassy state. Here we show how the distribution of the rotation speed of particles leads to the loss of hexatic order and results in the formation of a glassy state. As shown in Fig. 9a, the larger deviation from the averaged Re leads to the larger deviation from the average number of nearest neighbours (=6). With an increase in the variance of the distribution δ, more defects are produced and the hexatic order is eventually lost above δ≥0.2. We can also see that the the interparticle distance is larger for a particle rotating with a faster speed because of stronger hydrodynamic repulsive force, that is, Magnus force (Fig. 9). Both of these disorder effects are responsible for the formation of a glassy state: the number of the nearest neighbours and the average distance to the neighbours are both strongly correlated to the rotational speed of particles, which explains a wide enough distribution of the rotation speed results in the formation of a non-ergodic amorphous state instead of a hexatic ordered state. This glassy state is non-ergodic if we consider the particle configuration, yet maintains strong flow fields, which makes this state very unique. Reflecting the kinetic origin of interparticle interactions, the introduction of disorder in the dynamic quantity, Ω, is essential for avoiding the ordering, which is an interesting point unique to purely kinetic athermal systems.

Figure 8: Other interesting states formed in a system made of rotating particles.

(a) A glassy non-ergodic state formed in a system of rotating disks where the torque Γ acting on particles has a Gaussian distribution, whose normalized variance is δ=‹ΔΓ²›^1/2/Γ. Here Φ=0.157, the average Re ()=4.22 and δ=0.2. The colour of particles is green when the number of nearest neighbour particles NN is 6. For NN>6, the colour is red and for NN<6 blue. (b) δ-dependence of the hexatic-order parameter Ψ₆. Here Φ=0.157 and Re=7.76. With an increase in δ, the hexatic order monotonically decreases and the system eventually enters into a non-ergodic glassy state. (c) A plastic phase formed in a system made of rotating dumbbells (anticlockwise). The torque applied is the same for all particles. The rotation direction is anticlockwise. The system exhibits hexatic order at a certain range of Re, but without any orientational order of the axes of dumbbells. (d) Re-dependence of Ψ₆ for rotating dumbbells. We note that the transition is rather broad. The schematic image represents the distribution of volticity around a single rotating dumbbell (red: anticlockwise; blue: clockwise). (e) Phase separation of particles rotating clockwise (Ω) and anticlockwise (−Ω; Ω=0.155 (or Re=6.35)). Φ=0.157 and the number fraction of particles rotating clockwise is 0.5.

Figure 9: Correlation between local structure and rotation speed (or, Re) of each particle in a glassy state.

(a) Dependence of the number of nearest neighbours on Re for individual particles. The system size is 256² lattices, Φ=0.15, and the average value of Re, , is 4.2. We can see that the larger deviation from leads to the larger deviation from the average number of nearest neighbours (=6). (b) Dependence of the distance to nearest neighbour particles on Re for individual particles. The conditions are the same as the above. We can see that the interparticle distance is larger for a particle rotating with a faster speed (or, larger Re) because of stronger hydrodynamic repulsive force, that is, Magnus force.

We also find a plastic crystal-like state in a rotating particle pair (dumbbell) system (Fig. 8c) above a critical Re (Fig. 8d). This state is characterized by hexatic ordering of the centre of mass of disk pairs (dumbbells) without any orientational order in the axis directions of dumbbells. So we find for this type of athermal systems made of rotating particles almost all states seen in its thermodynamic counterparts, including a liquid, a hexatic phase, a glass and a plastic crystal. The only missing state is a liquid-crystalline state, but the lack of this state is natural consequence of the fact that the system is composed of rotating elements. We also note that the modification of the rotational direction leads to complex behaviours; for example, we can introduce phase demixing of particles rotating oppositely (Fig. 8e), which may be used to separate different types of passive and active rotors. In relation to this, it is worth noting that phase separation between particles rotating clockwise and anticlockwise was recently observed even without hydrodynamic interactions⁴⁰. It is interesting that such phase separation is observed in both systems with and without hydrodynamic interactions. It is also worth noting that the presence of regular arrays of vortices, for example, the triangle state, are predicted for an active polar film⁴¹. So far we have not seen such a regular state, but the similarity in the physics between the two systems implies that it might exist in a certain parameter range. This is an interesting problem for future study.

Discussion

It is remarkable that our athermal system where particles interact only via hydrodynamic interactions exhibits such rich phase (or more strictly, state) behaviour and reproduces almost all the physical states observed in its thermal counterpart. We hope that these phase behaviours will be observed experimentally. For this purpose, a quasi-2D version of the experimental setup used in refs 1, 4, 13, 14 may be suitable, since the 2D nature of hydrodynamic interactions is important. Here we have focused on the bulk behaviour of rotating disks to study the fundamental nature of dynamical phase behaviour from a viewpoint of nonequilibrium statistical physics. The effects of confinement on such a system are also quite interesting not only from a fundamental viewpoint, but also from a viewpoint of applications to microfluidics^42,43. Such effects on rotors in a fluid have recently been numerically studied by Götze and Gompper^22,23. It is quite interesting to study how such spatial confinements affect all the dynamical phases we reported and the transition between them.

Here it is worth stressing that even non-ergodic states of particles, such as hexatic, glassy and plastic crystal states, have strong hydrodynamic flow fields, which makes these states quite distinct from their thermal counterparts. The interesting and unique feature of hydrodynamic self-organization is that structural ordering is the consequence of self-organization of flow dissipating energy and thus even non-ergodic states are maintained by dynamical flow. In nature, there are many dynamical systems in which crucial interactions between elements are of purely hydrodynamic origin. The coexistence of linear and nonlinear hydrodynamic interactions, the resulting unconventional off-axis force, the finite propagation speed of the interactions and the significance of hydrodynamic degrees of freedom even for non-ergodic (apparently static) states lead to rich and non-trivial self-organization. We hope that our study sheds new light on hydrodynamic self-organization and stimulate further study on this intriguing problem.

Methods

Simulation method

Treating hydrodynamic interactions between colloids is difficult even for a thermal system. There are several methods such as Stokesian dynamics, lattice Boltzmann, smooth particle and FPD methods. Here we employ our FPD method^31,44, which has an advantage in its theoretical transparency and its applicability to a high Reynolds number (Re) regime. We can access a high Re regime rather easily particularly because a torque applied externally makes the flow field inside a fluid disk almost exactly that for a solid disk even at high Re.

Here we briefly explain the FPD method³¹ and the physical concept behind it. A particle whose centre of mass is located at r_i is represented by a smooth viscosity change as , where η_ℓ is the liquid viscosity and η_c is the viscosity inside a colloidal particle. The summation is taken over all N particles. φ_i represents particle i as , where a is the particle radius and ξ is the interface thickness. Then, the equation of motion to be solved is

with , where is the unit tensor. Here ρ is the mass density and we assume that the density of the liquid is the same as that of particles. ε(r) is the velocity field, and the pressure p is determined to satisfy the incompressibility condition . Here f_U(r) is the force density due to the interparticle interaction determined as , where U(r) is the interparticle potential, r_ij=r_i–r_j, and is the area of each particle. f_T(r) is the force density due to the torque: f_T(r)=α|r|φ(r)e_θ, where e_θ is the unit angular vector in the anticlockwise direction. α is the strength of the torque and α>0 leads to the anticlockwise rotation of a particle.

In our FPD method, the particle rigidity is approximately expressed by introducing the smooth viscosity profile, η(r). The approximation is better for a larger viscosity ratio η_c/η_ℓ and a smaller ξ/a. By multiplying both sides of Equation (1) by φ_i(r) and then performing its spatial integration, we can straightforwardly obtain an approximate equation of motion of particle i: M_idV_i/dt=F_i+K_i, where M_i=ρA=M and are the mass and the average velocity of particle i, respectively. On the right hand side, is the force arising from the interparticle interaction and the torque, and the force exerted by the fluid. Here we use the following approximate relation for an arbitrary tensor , where S_i is the surface of particle i and is the unit outward normal vector to S_i. In practical numerical calculations, the on-lattice velocity field, ε(r, t+Δt), is evaluated from the physical quantities at time t by Equation (1). Then, we move particle i off-lattice as a rigid body by r_t(t+Δt)=r_i(t)+Δt V_i(t+Δt), where Δt is the time increment of the numerical integration.

In our simulation, the units of length ℓ and time τ are related as τ=ℓ²/(η_ℓ/ρ), which sets both the scaled density and viscosity of the fluid region to unity. This τ is a time required for the fluid momentum to diffuse over a lattice size ℓ. The units of stress and energy are and , respectively. Furthermore, we set η_c/η_ℓ=50, Δt=0.003, ℓ=0.5, ξ=0.5 and a=6.4. We confirmed that this choice yields reliable results by comparing them wit the analytical solution for a single particle rotation (see, for example, Fig. 1a,b). The simulation box used was typically L²=256² lattices. To avoid cumbersome expressions, we will use the same characters for the scaled variables below. We solve the equation of motion (Equation (1)) by the marker-and-cell method with a staggered lattice under the periodic boundary condition.

Interparticle potentials

To mimic rotating hard disks, we employ the Weeks–Chandler–Andersen repulsive potential⁴⁵: U_jk(r)=4ε{(σ_jk/r)¹²−(σ_jk/r)⁶+1/4} for , otherwise U_jk(r)=0, where ε gives the energy scale, σ_jk=(σ_j+σ_k)/2 and σ_j represent the size of particle j.

Characterization of structures

The 2D radial distribution function g(r) was calculated as

which is the ratio of the ensemble average of the number density of particles existing in the region r~r+Δr to the average number density ρ=N/L². Here N is the number of particles in the simulation box, whose side length is L, and Δr is the increment of r.

Similarly, the spatial correlation of is calculated as³²

The spatial correlation of the bond-orientational order can then be characterized by .