Abstract
Ferroelectricity is a potentially crucial issue in halide perovskites, breakthrough materials in photovoltaic research. Using density functional theory simulations and symmetry analysis, we show that the lead-free perovskite iodide (FA)SnI3, containing the planar formamidinium cation FA, (NH2CHNH2)+, is ferroelectric. In fact, the perpendicular arrangement of FA planes, leading to a ‘weak’ polarization, is energetically more stable than parallel arrangements of FA planes, being either antiferroelectric or ‘strong’ ferroelectric. Moreover, we show that the ‘weak’ and ‘strong’ ferroelectric states with the polar axis along different crystallographic directions are energetically competing. Therefore, at least at low temperatures, an electric field could stabilize different states with the polarization rotated by π/4, resulting in a highly tunable ferroelectricity appealing for multistate logic. Intriguingly, the relatively strong spin–orbit coupling in noncentrosymmetric (FA)SnI3 gives rise to a co-existence of Rashba and Dresselhaus effects and to a spin texture that can be induced, tuned and switched by an electric field controlling the ferroelectric state.
Similar content being viewed by others
Introduction
One way to meet the growing energy demand of society, is the direct conversion of sunlight into electric power using photovoltaic cells. Increasing the efficiency of solar cells and relying on nontoxic abundant elements are absolutely vital to widely replace other means of energy production. Remarkably, in ferroelectric (FE) photovoltaic devices, where a homogeneous FE material acts as a light-absorbing layer, the electric field can help to separate electron–hole pairs, increasing the photocurrent1,2. Shift current has been proven to be a main mechanism of the bulk photovoltaic effect in FE oxides3,4.
Research interest in FE photovoltaic cells has been rekindled by the report that the lead iodide perovskite, (MA)PbI3, where MA refers to the methylammonium cation (CH3NH3)+, possesses ultrafast carrier mobility with a solar-energy-conversion efficiency of the order of 20% (ref. 5). In the class of organic/inorganic iodide perovskites (some of them remarkably crystallizing in a polar space group at room temperature)6, (MA)PbI3 has so far been the most promising material, because of a high absorption coefficient for the portion of the electromagnetic spectrum that passes through the atmosphere, combined with relatively long carrier lifetimes7. Mitzi et al.8,9 investigated the properties of layered organic–inorganic halides as thin-film transistors and light-emitting diodes. Photovoltaic properties were initially reported by Miyasaka and co-workers for the lead-based perosvkite10 reporting an efficiency ~2–4%, which subsequently increased to 6.5% (ref. 11). Later, it was observed that ‘meso-superstructured solar cells’12 result in even higher efficiency13. Recent experimental work14,15,16 has further improved the efficiency reaching now 17.9% (refs 7, 17).
Interestingly, these solar cells show many unusual characteristics, for instance, an anomalous hysteresis in the current–voltage curves18 that was tentatively related to their FE properties18. A full understanding of the hysteresis in (MA)PbI3 is essential for further progress and is likely to lead to performance improvements18,19. However, green energy requirements pose serious constraints on the use of Pb-based materials, thus raising the question whether Pb could be replaced by nontoxic elements, such as Sn (refs 20, 21, 22).
Intriguingly, owing to the presence of relatively heavy elements in halide perovskites, spin–orbit coupling (SOC), joint with the noncentrosymmetry of FE materials, might give rise to exotic spin-splitting phenomena23, such as Rashba or Dresselhaus effects24,25,26 occurring in the relativistic electronic structure of (nonmagnetic) semiconductors. While the Dresselhaus effect was originally formulated for three-dimensional (3D) solids as arising from bulk inversion asymmetry, whereas the Rashba effect was thought to derive from two-dimensional (2D) structural inversion asymmetry, this picture has been recently and nicely revised in an unified perspective27, following the discovery of Rashba effects in bulk materials28,29. Indeed, according to ref. 27, spin splittings can be classified on the basis of atomic site point groups lacking inversion symmetry, being either nonpolar (Dresselhaus) or polar (Rashba), implying also their possible co-existence. Within this framework, we remark that, despite strong interest in photovoltaic cells based on FE organic/inorganic iodide perovskites, experimental/theoretical studies concerning their FE behaviour and related relativistic effects are very few2,23,30,31,32,33,34.
The tin iodide (FA)SnI3, where FA refers to the formamidinium cation ((NH2)2CH)+, is quite unique in that each planar polar cation, FA, can change its dipole direction by rotating around its N···N axis, which is parallel to the crystallographic a axis. Thus, the arrangements of the FA cations in the bc plane determine whether (FA)SnI3 has a FE or antiferroelectric (anti-FE) structure, and how one FE structure is converted to another one with opposite polarization by coordinated rotations of the FA ions. On the basis of noncollinear-spin density functional theory (DFT) simulations, complemented with a careful symmetry analysis and relativistic GW calculations for the quasiparticle excitation energies, we study minimum energy structures of (FA)SnI3.
We find that the coordinated rotational motions of the FA cations can lead to a polarization reversal, as well as to a change of the directions of the polar axis, and we examine how the Dresselhaus and Rashba effects arising from SOC and FE polarization depend on the rotational arrangements of the FA cations. We show that, in the minimum energy structure, the plane of every FA cation is perpendicular to those of its surrounding four FA cations, giving rise to a ‘weak’ FE polarization. The ‘strong’ FE and ‘anti’ FE arrangements of the FA cations represent transition states on the pathway between two minimum energy structures with opposite polarization. By examining strong and weak FE arrangement of FA cations with the polar axis oriented in different directions, we show that these states have competing total energy. Our results for (FA)SnI3 open, therefore, the way to a highly tunable polarization and to a co-existence of electrically tunable ‘bulk’ Dresselhaus and Rashba effects.
Results
Structural and FE properties
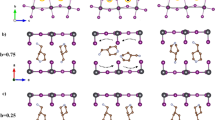
We start by considering the experimental structure of (FA)SnI3 with space group Amm2 (ref. 6; see strong FE structure in Fig. 1b). The FA cation is planar and polar with its dipole moment parallel to the C–H bond, as shown in Fig. 1a. The organic cations show a strong FE arrangement with all N···N axes parallel to the a axis, and the dipole pointing into the c direction. The iodine anions of the SnI3 framework are divided into axial and equatorial (Iax and Ieq, respectively). Here the Sn-Iax-Sn and Sn-Ieq-Sn bridges are parallel and perpendicular to the N...N axis of the FA cations. To evaluate the FE polarization from first principles, it is necessary to establish a centrosymmetric reference structure, which is converted to the noncentro-symmetric structures by applying a symmetry-breaking structural distortion. As reference structure, we adopt the anti-FE structure shown in Fig. 1b, in which two FA cations (referred as (I) and (II) in Fig. 1b) have an anti-FE arrangement along the b axis. In our search for the anti-FE→strong FE interconversion pathway, we considered out-of-phase rotations, where the FA cations on one column undergo a clockwise rotation, whereas those on the neighbouring column undergo a counterclockwise rotation around their N···N axes, as schematically depicted in Fig. 1b. Our DFT calculations show that the theoretical minimum energy structure is not the experimentally reported FE structure6. Instead, our lowest energy structure corresponds to an arrangement of the molecules resulting in the weak FE structure shown in Fig. 1b, where the C–H bonds are aligned along the face diagonal, and the C–H bonds in adjacent molecules are rotated by 90° with respect to each other. The anti-FE structure, as well as the experimentally reported strong FE structure6, represent transition states for the pathway that converts one minimum energy structure to another one with opposite polarization. These transition states are ~100 meV per formula-unit higher in energy than the low-energy weak FE structure (see Supplementary Note 1 and Supplementary Figure 1 for further structural details).
The internal atomic positions have been optimized, while the the volume and shape of the unit cell are fixed. (a) Details of the  cation making N-H···Ieq contacts; by symmetry, the molecular dipole moment is directed along the C–H bond. (b) The anti-FE (AFE), weak FE (WFE) and strong FE (SFE) structures as projected into the bc plane. (I) and (II) refer to the two FA cations in the unit cell; the curved arrows denote the rotations of the FA cations around the a axis. (c) The total energy profile as a function of θ, taking the anti-FE as reference configuration. In the inset we show the relative orientation of the molecular dipole. (d) The polarization as function of θ with c as the polar axis.
cation making N-H···Ieq contacts; by symmetry, the molecular dipole moment is directed along the C–H bond. (b) The anti-FE (AFE), weak FE (WFE) and strong FE (SFE) structures as projected into the bc plane. (I) and (II) refer to the two FA cations in the unit cell; the curved arrows denote the rotations of the FA cations around the a axis. (c) The total energy profile as a function of θ, taking the anti-FE as reference configuration. In the inset we show the relative orientation of the molecular dipole. (d) The polarization as function of θ with c as the polar axis.
Analysis of the FE polarization
The anti-FE structure has a centric space group Pmma, with no net polarization. The weak FE and strong FE structures are described by acentric space groups Pmc21 and Amm2, respectively, and both display a net FE polarization. In the following, we consider the total polarization, that is, the sum of ionic and electronic contributions. We consider the path from the anti-FE to strong FE structures passing through the weak FE structure by introducing an angle θ. This angle specifies the direction of the C–H bond, whereas the N···N axis is always roughly parallel to the a axis (see Fig. 1b,c). For θ=0, π/4 and π/2, we obtain the anti-FE, weak FE and strong FE structures, respectively. With this choice, the polarization is always parallel to the c axis, and since all structures possess a band gap, the change of the polarization along the pathway can be calculated using the Berry-phase approach35. The two end points (anti-FE and strong FE) are kept fixed, whereas the internal coordinates of all other structures are fully optimized using the nudged elastic band method36. This approach allows us to take into account the coupling between the molecular rotations and the distortions of the framework (see Supplementary Note 2 and Supplementary Figure 2). The total-energy variation and the total polarization as a function of θ are shown in Fig. 1c,d, respectively. The energy is lowered when θ increases, exhibiting a minimum at the weak FE arrangement. Then, the energy increases again towards the strong FE arrangement, which is slightly more stable than the anti-FE one. The polarization sets out from zero for the anti-FE structure, exhibits a maximum between the anti-FE and weak FE structures and then monotonically decreases towards the strong FE state. The overall polarization vanishes and switches its direction along the pathway: this is a result of the balance between opposite contributions of the local FA dipoles and of the SnI3 framework, as further detailed in the Supplementary Note 2 and Supplementary Figure 2. The calculated polarization at the DFT level is Pweak−FE=0.88 μC cm−2 and Pstrong−FE=−5.35 μC cm−2 for the weak FE and strong FE structures, respectively. We caution the reader that we limited our study to the smallest unit cell compatible with an antiferroelectric reference structure. Lower energy structures may be possible when using, for example, larger unit cells. However, this goes beyond the present study, since our aim is to highlight the band-structure features due to the interplay between ferroelectricity and SOC and, for this purpose, the smallest unit cell is the most reasonable system to study.
We also remark that other polar arrangements for the molecular dipole moments in the pseudocubic structure are possible. If the b and c lattice parameters are equal, which is roughly observed experimentally, states with polarization parallel to these two directions are symmetry equivalent. However, we can also choose to align the C–H bond in the anti-FE and strong FE structure along the (b+c) direction (that is, [011]) instead of the b ([010]) or c ([001]) axis. Then, the dipole moment is also parallel to [011] in the strong FE structure. Analogously, it is possible to have weak FE states with polar axis along the [011] direction. The calculated energy variations are shown in Fig. 2b. It is evident that for polarizations along [011] the energy variations between the anti-FE, weak FE and strong FE structures are negligible, and that the weak FE structure with polarization along [001] is lower in energy than any of the other structures. Our analysis of the structures shows that short N-H···Ieq and N-H···Ieq distances occur only for the weak FE structure with the dipole moments parallel to the b or c axis (compare Fig. 1b and Supplementary Note 1 and 2). An analysis of the hydrogen bond lengths for the different structures are given in Supplementary Note 3 (see also Supplementary Figure 3, 4 and Supplementary Table I). Thus, the stability of the weak FE structures is driven by N-H···Ieq hydrogen bonds. Since the latter interactions are weak, it is expected that the polarization orientation can be readily rotated from one direction to another by, for example, applying an external electric field, thus putting forward (FA)SnI3 as a highly tunable FE. Finally, a comment is in order. Halide perovskites at finite temperatures are likely to exhibit disorder in the molecular orientation due to the associated configurational entropy. Hence, these materials are likely to be paraelectric at room temperature. Indeed, significant disorder was predicted, for example, for CH3NH3PbI3 in ref. 37 from molecular dynamics simulations37.
Co-existence of electrically tunable Dresselhaus and Rashba effects
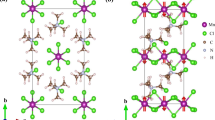
The Brillouin Zone of the strong FE structure of (FA)SnI3 (with the FA dipole direction fixed along [001]) is presented in Fig. 3a, and the related band dispersion is shown in Fig. 3b, indicating the band gap occurring around the X point, as highlighted by the red circle. By projecting the orbitals onto s and p states at the ions, we can determine the predominant character of each band. The conduction band minimum (CBM) shows predominantly Sn 5p orbital character, whereas the valence band maximum (VBM) is mainly composed of Sn 5s and I 5p states. As clearly visible in Fig. 3c, the valence and conduction bands (otherwise twofold degenerate in the absence of SOC) are spin-split and shifted in the k-space away from the high-symmetry point X in presence of SOC, therefore resulting in the so-called ‘inner’ and ‘outer’ branches. In the case of spin-splitting effects, it is customary26 to define (i) a ‘momentum offset’ (in the k-space), as the difference between the k-point where the band edge is located (including SOC) and the high-symmetry point (X in our case); (ii) an energy splitting, corresponding to the difference between the energy value of a spin-split band at the high-symmetry point (X) and at the band edge. In our case, the energy splittings at the CBM are greater than those at the VBM, and are ~9.4 and 7.7 meV along the  and
and  directions, respectively (the
directions, respectively (the  and
and  directions are highlighted in the blue inset of Fig. 3a). The momentum offsets at the CBM are estimated to be 0.016 Å−1 along
directions are highlighted in the blue inset of Fig. 3a). The momentum offsets at the CBM are estimated to be 0.016 Å−1 along  and 0.013 Å−1 along
and 0.013 Å−1 along  , whereas those for the VBM are negligible, thus giving rise to a ‘formally indirect’ band gap. Of possible relevance for photovoltaic applications, we note that the different momentum offsets in the conduction and valence bands can possibly affect the probability of radiative recombination of the photo-induced electrons and holes, due to the absence of a formal direct gap38. These considerations remain however at the speculative level, as a quantitative evaluation of radiative and nonradiative recombination rates (with and without SOC) is beyond the scope of the present work.
, whereas those for the VBM are negligible, thus giving rise to a ‘formally indirect’ band gap. Of possible relevance for photovoltaic applications, we note that the different momentum offsets in the conduction and valence bands can possibly affect the probability of radiative recombination of the photo-induced electrons and holes, due to the absence of a formal direct gap38. These considerations remain however at the speculative level, as a quantitative evaluation of radiative and nonradiative recombination rates (with and without SOC) is beyond the scope of the present work.
(a) Brillouin zones highlighting the high-symmetry points (top) and the plane orthogonal to the polar axis around the X point (bottom). (b,c) DFT band dispersion relations along the whole Brillouin zone and around the X point. The GW bands are given in the Supplementary Note 6 and Supplementary Figure 5. (d) DFT energy profiles for the CBM outer (left) and inner (right) branches of the Rashba—Dresselhaus spin split bands. (e,f) Relative DFT spin textures as a function of the ferroelectric polarization. (e) P-up and outer branch (left), P-up and inner branch (right). (f) P-down and outer branch (left), P-down and outer branch (right).
Let us now focus on the spin texture of those bands where spin-splitting effects are larger, that is, the CBM. In the plane identified by the  and
and  directions (perpendicular to the FE polarization), the outer branch of the spin-split conduction band shows two symmetric energy minima along the
directions (perpendicular to the FE polarization), the outer branch of the spin-split conduction band shows two symmetric energy minima along the  direction, while the inner branch displays a cone shape (Fig. 3d). These two split bands present nontrivial and opposite spin textures, with spins orthogonal to the crystal momenta along the
direction, while the inner branch displays a cone shape (Fig. 3d). These two split bands present nontrivial and opposite spin textures, with spins orthogonal to the crystal momenta along the  and
and  axes, but radial along the directions rotated by π/4 (Fig. 3e). Such a spin texture differs significantly from the one recently predicted for β-(MA)PbI3, β-(MA)SnI3 and ortho-(MA)SbBr3 FE halide perovskites, where spins rotate in a circular way on constant energy contours, according to a Rashba-type spin splitting23. This calls for a deeper understanding, which we provide in terms of k·p Hamiltonian modelling. Indeed, the SOC-induced band splitting around the CBM can be understood by inspecting the expression of symmetry-allowed terms in the k·p Hamiltonian around the gap26. The expression of the effective Hamiltonian is strictly fixed by symmetry. Since the X point preserves time-reversal symmetry, a Kramers pair is observed at the CBM, which is split by SOC away from X. The doublet
axes, but radial along the directions rotated by π/4 (Fig. 3e). Such a spin texture differs significantly from the one recently predicted for β-(MA)PbI3, β-(MA)SnI3 and ortho-(MA)SbBr3 FE halide perovskites, where spins rotate in a circular way on constant energy contours, according to a Rashba-type spin splitting23. This calls for a deeper understanding, which we provide in terms of k·p Hamiltonian modelling. Indeed, the SOC-induced band splitting around the CBM can be understood by inspecting the expression of symmetry-allowed terms in the k·p Hamiltonian around the gap26. The expression of the effective Hamiltonian is strictly fixed by symmetry. Since the X point preserves time-reversal symmetry, a Kramers pair is observed at the CBM, which is split by SOC away from X. The doublet  is well described in a natural basis according to the total angular momentum J=1/2 (refs 23, 31), transforming as the usual Pauli matrices σx, σy and σz. The general expression of the k·p Hamiltonian can hereafter be inferred by taking into account—besides time reversal—the point-group symmetry at X, which is C2v. To first order in k*, the SOC-induced term entering the effective Hamiltonian under the considered symmetries takes the form
is well described in a natural basis according to the total angular momentum J=1/2 (refs 23, 31), transforming as the usual Pauli matrices σx, σy and σz. The general expression of the k·p Hamiltonian can hereafter be inferred by taking into account—besides time reversal—the point-group symmetry at X, which is C2v. To first order in k*, the SOC-induced term entering the effective Hamiltonian under the considered symmetries takes the form  , where α, β denote material-dependent constants (Supplementary Note 4 and Supplementary Table II). These constants are not required to be equal under the C2v symmetry, in contrast to the aforementioned case of (MA)PbI3, where a C4v point symmetry imposes α=β, hence leading to a pure Rashba-like term23. The SOC term acquires a more transparent form if the local reference system is rotated by π/4 around
, where α, β denote material-dependent constants (Supplementary Note 4 and Supplementary Table II). These constants are not required to be equal under the C2v symmetry, in contrast to the aforementioned case of (MA)PbI3, where a C4v point symmetry imposes α=β, hence leading to a pure Rashba-like term23. The SOC term acquires a more transparent form if the local reference system is rotated by π/4 around  (that is, the polar axis); in the rotated system the SOC term is rewritten as
(that is, the polar axis); in the rotated system the SOC term is rewritten as  , where the first and second terms describe a Rashba and a linear Dresselhaus effects26, respectively, with coupling constants αR=(α+β)/2 and αD=(α−β)/2. Such a co-existence of Dresselhaus and Rashba terms has been extensively studied in semiconductor quantum wells with C2v point symmetry, as n-type heterostructures such as InAs/Al0.3Ga0.7Sb single quantum well39 or GaAs/InGaAs quantum wells40. In the plane of
, where the first and second terms describe a Rashba and a linear Dresselhaus effects26, respectively, with coupling constants αR=(α+β)/2 and αD=(α−β)/2. Such a co-existence of Dresselhaus and Rashba terms has been extensively studied in semiconductor quantum wells with C2v point symmetry, as n-type heterostructures such as InAs/Al0.3Ga0.7Sb single quantum well39 or GaAs/InGaAs quantum wells40. In the plane of  and
and  , the band dispersion close to the CBM shows a spin-splitting correction
, the band dispersion close to the CBM shows a spin-splitting correction  , where
, where  , which nicely accounts for the predicted band shapes and the two symmetric energy minima along the
, which nicely accounts for the predicted band shapes and the two symmetric energy minima along the  direction when |β|>|α|. By fitting the conduction bands along
direction when |β|>|α|. By fitting the conduction bands along  ,
,  with this spin-splitting correction, we find that at the CBM the Rashba and Dresselhaus coupling terms are αR=0.003 eVÅ and αD=1.19 eVÅ , respectively (values at the VBM cannot be reliably evaluated due to negligible spin splitting). This shows that a rather large Dresselhaus coupling is present and that the Dresselhaus-like term dominates over the Rashba-like, thus explaining the origin of spin textures in (FA)SnI3 that strongly resemble pure Dresselhaus-type ones (Supplementary Note 4,5 and Supplementary Table II).
with this spin-splitting correction, we find that at the CBM the Rashba and Dresselhaus coupling terms are αR=0.003 eVÅ and αD=1.19 eVÅ , respectively (values at the VBM cannot be reliably evaluated due to negligible spin splitting). This shows that a rather large Dresselhaus coupling is present and that the Dresselhaus-like term dominates over the Rashba-like, thus explaining the origin of spin textures in (FA)SnI3 that strongly resemble pure Dresselhaus-type ones (Supplementary Note 4,5 and Supplementary Table II).
For an increased accuracy, we estimate, within the GW approximation (Supplementary Note 6 and Supplementary Figure 5), the spin splittings at the CBM to be as large as 14.8 and 10.2 meV along  and
and  directions, respectively, at momentum offsets from X of 0.022 and 0.018 Å−1, respectively. The resulting Rashba/Dresselhaus parameters, estimated within GW, αR=0.08 eVÅ and αD=1.24 eVÅ, are not significantly different from those obtained from bare-DFT, thus reinforcing the quantitative DFT estimates made so far.
directions, respectively, at momentum offsets from X of 0.022 and 0.018 Å−1, respectively. The resulting Rashba/Dresselhaus parameters, estimated within GW, αR=0.08 eVÅ and αD=1.24 eVÅ, are not significantly different from those obtained from bare-DFT, thus reinforcing the quantitative DFT estimates made so far.
Interplay between ferroelectricity and SOC
Since the bulk Rashba αR and Dresselhaus αD constants strongly depend on the potential gradient and inversion-asymmetric environment of the active ions within the material, in turn giving rise to ferroelectricity, one can anticipate changes in the spin splittings and spin texture depending on both the direction and sense of FE polarization. Indeed, the reversal of the polar axis via the application of an external electric field is expected to lead to a switching of the spin texture, as predicted in theoretical studies for bulk GeTe (refs 29) and, later on, for β-(MA)PbI3, β-(MA)SnI3 and ortho-(MA)SbBr3 FE halide perovskites23. In Fig. 3e,f we show that the Dresselhaus-like spin textures at the CBM is indeed reversed when going from −P to +P in the FE structure. Qualitatively, the same behaviour is found for the weak FE arrangement, even though the spin-splitting effects are slightly reduced, consistent with the smaller calculated value of polarization.
As for the effect of rotating the polar axis from [001] to [011], the same qualitative picture is expected to hold for spin-splitting effects and switchable spin textures in the plane perpendicular to P. In fact, even though the point-group symmetry at the X point is lowered to Cs—consisting of a mirror operation whose plane contains the polar axis (taken parallel to  ) and
) and  —the effective SOC Hamiltonian in the chosen reference frame takes exactly the same expression found for C2v symmetry, underlying a co-existence of Rashba and Dresselhaus terms whose relative strength depends again on material specifics. Remarkably, however, we find that the spin splittings in the VBM are larger than in the CBM, where they are almost negligible, when the polar axis is parallel to [011]. Such a change in the electronic structure can be roughly ascribed to the different response of the SnI3 framework when the dipole direction of the organic cations is rotated, resulting in different hybridization paths whose interplay with the atomic SOC is ultimately responsible for the observed spin-splitting phenomena. The VBM splitting for the strong FE structure of (FA)SnI3 in which the FA dipole direction is fixed along [011] is as large as 5.4 meV (3.4 meV) along
—the effective SOC Hamiltonian in the chosen reference frame takes exactly the same expression found for C2v symmetry, underlying a co-existence of Rashba and Dresselhaus terms whose relative strength depends again on material specifics. Remarkably, however, we find that the spin splittings in the VBM are larger than in the CBM, where they are almost negligible, when the polar axis is parallel to [011]. Such a change in the electronic structure can be roughly ascribed to the different response of the SnI3 framework when the dipole direction of the organic cations is rotated, resulting in different hybridization paths whose interplay with the atomic SOC is ultimately responsible for the observed spin-splitting phenomena. The VBM splitting for the strong FE structure of (FA)SnI3 in which the FA dipole direction is fixed along [011] is as large as 5.4 meV (3.4 meV) along  with a momentum offset of 0.008 Å−1 (0.007 Å−1); the corresponding estimated Rashba/Dresselhaus parameters are αR=1.10 eVÅ and αD=0.18 eVÅ (as before, values at the CBM cannot be reliably evaluated due to negligible spin splitting), resulting in a Rashba-like spin textures with spins rotating in a circular way on constant energy contours. This is clearly seen in Fig. 4 where we show: (a) the unit cell and the polarization along the [011] as well as the plane perpendicular to it; (b) spin splitting of the bands along the two perpendicular directions to the polarization (note that the spin splitting is larger in the valence than in the conduction bands); (c) spin texture in the plane perpendicular to the polarization, showing the characteristic Rashba-like texture, with typical spin switching between the inner and outer branch.
with a momentum offset of 0.008 Å−1 (0.007 Å−1); the corresponding estimated Rashba/Dresselhaus parameters are αR=1.10 eVÅ and αD=0.18 eVÅ (as before, values at the CBM cannot be reliably evaluated due to negligible spin splitting), resulting in a Rashba-like spin textures with spins rotating in a circular way on constant energy contours. This is clearly seen in Fig. 4 where we show: (a) the unit cell and the polarization along the [011] as well as the plane perpendicular to it; (b) spin splitting of the bands along the two perpendicular directions to the polarization (note that the spin splitting is larger in the valence than in the conduction bands); (c) spin texture in the plane perpendicular to the polarization, showing the characteristic Rashba-like texture, with typical spin switching between the inner and outer branch.
Recapitulating this section, our results suggest that spin-splitting effects can be modulated in both the CBM and VBM depending on the polarization direction. When FE polarization is switched from P to −P while keeping the polar axis fixed, the spin textures are found to be fully reversed. On the other hand, the predominance of Dresselhaus and Rashba effects appears to be electrically tunable, as the former (latter) seems to dominate at the CBM (VBM) for polarization along the [001] ([011]) axis.
Discussion
In summary, we have studied a new low-energy structure for (FA)SnI3 with weak FE order and polarization along the b or c axis. The small-energy barriers between the minimum energy structures and the transition states (namely, strong FE and anti-FE structures) imply that, at least at low temperature, by means of an external electric field, a FE polarization can be induced (from the anti-FE or disordered to the weak FE structure), can be tuned in magnitude (from the weak to the strong FE structure) and in direction (for instance from the [001] to the [011] axis). Therefore, (FA)SnI3 is expected to exhibit a highly tunable polarization. A sort of similar ‘FE anisotropy’ was previously suggested, by analogy with the magnetic counterpart, in the context of charge-ordered multiferroics41; however, materials that possess that kind of behaviour are very rare, at variance with more common halide perovskites.
As the Rashba–Dresselhaus spin texture is tightly linked to the polarization direction, the highly tunable polarization in (FA)SnI3 opens exciting perspectives in spintronics. The possibility to permanently induce/tune/switch the direction of polarization via an electric field implies a corresponding control over the spin degrees of freedom23,29. Owing to the high tunability of the FE polarization, the (controllable) co-existence of Rashba and Dresselhaus effects in (FA)SnI3 can provide new ways to exploit the spin degrees of freedom in photovoltaics.
The energy band gap estimated for (FA)SnI3 based on GW calculations is 1.07 eV, which may be too small for efficient photovoltaic applications. However, one could improve the photovoltaic efficiency, as the electronic properties (in particular, the band gap) can be tuned by a suitable choice of the organic or inorganic components42,43. Furthermore, the spin texture of (FA)SnI3, due to the tunable Rashba–Dresselhaus effects, may give rise to several unique features in the optical properties, such as generating a magnetophotocurrent with possible spin polarization on breaking the time-reversal symmetry of the bulk spin-split bands by applying an external magnetic field44,45.
Since the presence of FE may enhance the photocurrent because of the natural separation of electron and holes1,2, the tunability of the magnitude and directions of polarization can introduce an additional degree of freedom for collecting the photocurrent, that is, anisotropy of the photocurrent. In this case, one can process the information by electrically writing (for example, stabilizing a given FE state) and optically/electrically reading (for example, detecting a different photocurrent) for a given FE state. Finally, one may envisage the photocurrent being used to extract direct information on the different SOC-induced contributions, such as Rashba and Dresselhaus terms, for example, by means of the photogalvanic effect39. All these facts could have interesting applications benefiting from the peculiar electronic and photovoltaic properties of the material, thus opening the possibility of development of new optoelectronic devices19.
Methods
Computational approach
Our DFT calculations for (FA)SnI3 were carried out using the projector-augmented wave method implemented in VASP using the PBEsol functional46,47,48 within a noncollinear spin set-up and including SOC. Test calculations have also been performed using the Heyd–Scuseria–Ernzerhof-screened hybrid density functional49. We started from the α-phase of (FA)SnI3, refined at T=340 K, in the Amm2 space group6. The atom positions were optimized until the residual forces were smaller than 0.001 eV Å−1 with the plane-wave cutoff energy of 500 eV and a 6 × 4 × 4 Monkhorst–Pack grid of k-points. Systematic convergence tests with respect to the energy cutoff and k-point sampling were performed, although not shown here. The FE polarization was calculated using the Berry phase method35. The use of different van der Waals functionals50 did not lead to significant differences, demonstrating that the main results presented here are robust. Intermediate structures between θ=0 and θ=π/2 in the analysis of the FE polarization were relaxed using the nudged elastic band method36 to prevent the formamidinium molecules in the intermediate configurations from rotating back to the minimum energy configuration. An accurate quasiparticle electronic structure was obtained by using a partially self-consistent GW0+SOC procedure51,52, where we have updated the eigenvalues by iterating the Green’s function G while keeping the screening properties W0 constant at the DFT level. Three iterations were sufficient to achieved a converged solution. A plane-wave basis with an energy cutoff of 420 eV with ~2,100 empty bands on a Γ-centred 4 × 4 × 4 k-mesh and 128 points on the frequency grid are needed to get a converged band structure. The energy cutoff for the response function was set to 150 eV. We made use of the VASP2WANNIER90 interface to interpolate the band structures to a finer grid53,54. The search of the centric structure, as well as the symmetry analysis, was performed using the PSEUDO and AMPLIMODES tools on the Bilbao Crystallographic Server55,56. Figures are plotted using the VESTA package57.
Additional information
How to cite this article: Stroppa, A. et al. Tunable ferroelectric polarization and its interplay with spin–orbit coupling in tin iodide perovskites. Nat. Commun. 5:5900 doi: 10.1038/ncomms6900 (2014).
References
Yuan, Y. B., Xiao, Z. G., Yang, B. & Huang, J. S. Arising applications of ferroelectric materials in photovoltaic devices. J. Mater. Chem. A 2, 6027–6041 (2014).
Frost, J. M. et al. Atomistic origins of high-performance in hybrid halide perovskite solar cells. Nano Lett. 14, 2584–2590 (2014).
Young, S. M. & Rappe, A. M. First principles calculation of the shift current photovoltaic effect in ferroelectrics. Phys. Rev. Lett. 109, 116601 (2012).
Young, S. M., Zheng, F. & Rappe, A. M. First-principles calculation of the bulk photovoltaic effect in bismuth ferrite. Phys. Rev. Lett. 109, 236601 (2012).
Park, N. G. Organometal perovskite light absorbers toward a 20% efficiency low-cost solid-state mesoscopic solar cell. J. Phys. Chem. Lett. 4, 2423–2429 (2013).
Stoumpos, C. C., Malliakas, C. D. & Kanatzidis, M. G. Semiconducting tin and lead iodide perovskites with organic cations: phase transitions, high mobilities, and near-infrared photoluminescent properties. Inorg. Chem. 52, 9019–9038 (2013).
Green, M. A., Ho-Baillie, A. & Snaith, H. J. The emergence of perovskite solar cells. Nat. Photon 8, 506–514 (2014).
Mitzi, D. B., Feild, C. A., Harrison, W. T. A. & Guloy, A. M. Conducting tin halides with a layered organic-based perovskite structure. Nature 369, 467–469 (1994).
Mitzi, D. B., Wang, S., Feild, C. A., Chess, C. A. & Guloy, A. M. Conducting layered organic-inorganic halides containing <110>-oriented perosvkite sheets. Science 267, 1473–1476 (1995).
Kojima, A., Teshima, K., Shirai, Y. & Miyasaka, T. Organometal halide Perovksite as visible-light sensitizers for photovoltaic cells. J. Am. Chem. Soc. 131, 6050–6051 (2009).
Im, J.-H., Lee, C.-R., Lee, J.-W., Park, S.-W. & Park, N.-G. 6.5% efficient perovskite quantum-dot-sensitized solar cell. Nanoscale 3, 4088–4093 (2011).
Lee, M. M., Teuscher, J., Miyasaka, T., Murakami, T. N. & Snaith, H. J. Efficient hybrid solar cells based on meso-superstructured organometal halide perovkites. Science 338, 643–647 (2012).
Liu, M., Johnston, M. B. & Snaith, H. J. Efficient planar heterojunction perovskite solar cells by vapour deposition. Nature 501, 395–398 (2013).
Heo, J. H. et al. Efficient inorganic-organic hybrid heterojunction solar cells containing perovskite compound and polymeric hole conductors. Nat. Photon 7, 486–491 (2013).
Burschka, J. et al. Sequential deposition as a route to high-performance perovskite-sensitized solar cells. Nature 499, 316–319 (2013).
Stranks, S. D. et al. Electron-hole diffusion lengths exceeding 1 micrometer in an organometal trihalide perovskite absorber. Science 342, 341–344 (2013).
Snaith, H. J. Perovskites: the emergence of a new era for low-cost, high-efficiency solar cells. J. Phys. Chem. Lett. 4, 3623–3630 (2013).
Snaith, H. J. et al. Anomalous hysteresis in perovskite solar cells. J. Phys. Chem. Lett. 5, 1511–1515 (2014).
Juarez-Perez, E. J. et al. Photoinduced giant dielectric constant in lead halide perovskite solar cells. J. Phys. Chem. Lett. 5, 2390–2394 (2014).
Noel, K. N. et al. Lead-free organic-inorganic tin halide perovskites for photovoltaic applications. Energy Environ. Sci. 7, 3061–3068 (2014).
Hao, F., Stoumpos, C. C., Cao, D. H., Chang, R. P. H. & Kanatzidis, M. G. Lead-free solid-state organic-inorganic halide perovskite solar cells. Nat. Photon 8, 489–494 (2014).
Dusastre, V. Materials for clean energy. Nature 414, 331 (2001).
Kim, M., Im, J., Freeman, A. J., Ihm, J. & Jin, H. Switchable S=1/2 and J=1/2 Rashba bands in ferroelectric halide perovskites. Proc. Natl Acad. Sci. USA 111, 6900–6904 (2014).
Rashba, E. I. Sov. Phys. Solid State 2, 1109 (1960).
Dresselhaus, G. Phys. Rev. B 100, 580 (1955).
Winkler, R. Spin-Orbit Coupling Effects in Two-Dimensional Electron and Hole Systems Springer-Verlag (2003).
Zhang, X. W., Liu, Q. H., Luo, J. W., Freeman, A. J. & Zunger, A. Hidden spin polarization in inversion-symmetric bulk crystals. Nat. Phys. 10, 387–393 (2014).
Ishizaka, K. et al. Giant Rashba-type spin splitting in bulk BiTeI. Nat. Mater. 10, 521 (2011).
Di Sante, D., Barone, P., Bertacco, R. & Picozzi, S. Electric control of the giant rashba effect in bulk GeTe. Adv. Mater. 25, 509–513 (2013).
Mosconi, E., Amat, A., Nazeeruddin, M. K., Graetzel, M. & De Angelis, F. First-principles modeling of mixed halide organometal perovskites for photovoltaic applications. J. Phys. Chem. C 117, 13902–13913 (2013).
Even, J., Pedesseau, L., Jancu, J.-M. & Katan, C. Importance of spin-orbit coupling in hybrid organic/inorganic perovskites for photovoltaic applications. J. Phys. Chem. Lett. 4, 2999–3005 (2013).
Brivio, F., Walker, A. B. & Walsh, A. Structural and electronic properties of hybrid perovskites for high-efficiency thin-film photovoltaics from first-principles. APL Mat. 1, 042111 (2014).
Kutes, Y. et al. J. Phys. Chem. Lett. 5, 3335–3339 (2014).
Giorgi, G., Fujisawa, J. I., Segawa, H. & Yamashita, K. Small photocarrier effective masses featuring ambipolar transport in methylammonium lead iodide perovskite: a density functional analysis. J. Phys. Chem. Lett. 4, 4213–4216 (2013).
King-Smith, R. D. & Vanderbilt, D. Theory of polarization of crystalline solids. Phys. Rev. B 47, 1651–1654 (1993).
Mills, G., Jonsson, H. & Schenter, G. K. Reversible work transition state theory: application to dissociative adsorption of hydrogen. Surf. Sci. 324, 305–337 (1995).
Frost, J. M., Butler, K. T. & Walsh, A. Molecular ferroelectric contributions to anomalous hysteresis in hybrid perovskite solar cells. APL Mat. 2, 081506-1–081506-10 (2014).
Amat, A. et al. Cation-induced band-gap tuning in organohalide perovskites: interplay of spinorbit coupling and octahedra tilting. NanoLett 14, 3608–3616 (2014).
Ganichev, S. D. et al. Experimental separation of rashba and dresselhaus spin splittings in semiconductor quantum wells. Phys. Rev. Lett. 92, 256601 (2004).
Meier, L. et al. Measurement of Rashba and Dresselhaus spin-orbit magnetic fields. Nat. Phys. 3, 650–654 (2007).
Yamauchi, K. & Picozzi, S. Interplay between charge order, ferroelectricity, and ferroelasticity: tungsten bronze structures as a playground for multiferroicity. Phys. Rev. Lett. 105, 107202 (2010).
Borriello, I., Cantele, G. & Ninno, D. Ab initio investigation of hybrid organic-inorganic perovskites based on tin halides. Phys. Rev. B 77, 235214 (2008).
Chiarella, F. et al. Combined experimental and theoretical investigation of optical, structural, and electronic properties of CH3NH3SnX3 thin films (X=Cl,Br). Phys. Rev. B 77, 045129 (2008).
Ogawa, N., Bahramy, M. S., Murakawa, H., Kaneko, Y. & Tokura, Y. Magnetophotocurrent in BiTeI with Rashba spin-split bands. Phys. Rev. B 88, 035130 (2013).
Lee, J. S. et al. Optical response of relativistic electrons in the polar BiTeI semiconductor. Phys. Rev. Lett. 107, 117401 (2011).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Perdew, J. P. et al. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 100, 136406–136410 (2008).
Heyd, J., Scuseria, G. E. & Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 118, 8207–8215 (2003).
Grimme, S. Accurate description of van der Waals complexes by density functional theory including empirical corrections. J. Comput. Chem. 25, 1463–1473 (2004).
Hedin, L. New method for calculating the one-particle Green's function with application to the electron-gas problem. Phys. Rev. 139, A796 (1965).
Shishkin, M. & Kresse, G. Implementation and performance of the frequency-dependent GW method within the PAW framework. Phys. Rev. B 74, 035101 (2006).
Mostofi, A. A. et al. Wannier90: a tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 178, 685 (2008).
Franchini, C. et al. Maximally localized Wannier functions in LaMnO3 within PBE+U, hybrid functionals and partially self-consistent GW: an efficient route to construct ab initio tight-binding parameters for eg perovskites. J. Phys. Condens. Matter. 24, 235602 (2012).
Kroumova, E. et al. PSEUDO: a program for a pseudosymmetry search. J. Appl. Cryst. 34, 783–784 (2001).
Orobengoa, D., Capillas, C., Aroyo, M. I. & Perez-Mato, J. M. AMPLIMODES:symmetry-mode analysis on the Bilbao Crystallographic Server. J. Appl. Cryst. A42, 820–833 (2009).
Momma, K. & Izumi, F. VESTA: a three-dimensional visualization system for electronic and structural analysis. J. Appl. Crystallogr. 41, 653–658 (2008).
Acknowledgements
A.S. would like to thank T. Bucko, M. Marsman and M. Perez-Mato for useful discussions. A.S. and S.P. would like to thank F. De Angelis for interesting discussions. A.S. acknowledges support from CNR Short Term Mobility programme prot. AMMCNT-CNR 0026336 and the kind hospitality of Professor J. van den Brink (IFW Leibniz Institute, Dresden, Germany) where this work was finalized. A.S. and M.-H.W. are thankful to the HPC Center of NCSU for computing resources. M.B. is funded by the Austrian Science Fund (FWF) within the the special research programme IR-ON (F25).
Author information
Authors and Affiliations
Contributions
A.S. and S.P. conceived the project; A.S. performed DFT and symmetry mode analysis on FE properties. D.D.S. performed DFT+SOC calculations and the Rashba/Dresselhaus analysis; P.B. performed the model Hamiltonian analysis; M.B., C.F. and G.K. performed GW calculations; G.K., M.-H.W. and S.P. supervised the project. All the authors contributed to discussions and writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-5, Supplementary Tables 1-2, Supplementary Notes 1-6, and Supplementary References. (PDF 916 kb)
Rights and permissions
About this article
Cite this article
Stroppa, A., Di Sante, D., Barone, P. et al. Tunable ferroelectric polarization and its interplay with spin–orbit coupling in tin iodide perovskites. Nat Commun 5, 5900 (2014). https://doi.org/10.1038/ncomms6900
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms6900
This article is cited by
-
Colloid driven low supersaturation crystallization for atomically thin Bismuth halide perovskite
Nature Communications (2023)
-
Progress of hidden spin polarization in inversion-symmetric crystals
Science China Physics, Mechanics & Astronomy (2022)
-
Tunable spin textures in polar antiferromagnetic hybrid organic–inorganic perovskites by electric and magnetic fields
npj Computational Materials (2020)
-
Insulator-to-conductor transition driven by the Rashba–Zeeman effect
npj Computational Materials (2020)
-
Defect-mediated Rashba engineering for optimizing electrical transport in thermoelectric BiTeI
npj Computational Materials (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.