Abstract
Central spin decoherence caused by nuclear spin baths is often a critical issue in various quantum computing schemes, and it has also been used for sensing single-nuclear spins. Recent theoretical studies suggest that central spin decoherence can act as a probe of many-body physics in spin baths; however, identification and detection of many-body correlations of nuclear spins in nanoscale systems are highly challenging. Here, taking a phosphorus donor electron spin in a 29Si nuclear spin bath as our model system, we discover both theoretically and experimentally that many-body correlations in nanoscale nuclear spin baths produce identifiable signatures in decoherence of the central spin under multiple-pulse dynamical decoupling control. We demonstrate that under control by an odd or even number of pulses, the central spin decoherence is principally caused by second- or fourth-order nuclear spin correlations, respectively. This study marks an important step toward studying many-body physics using spin qubits.
Similar content being viewed by others
Introduction
Decoherence of a central spin in a solid-state environment is not only an ideal model problem for understanding the foundation of quantum physics1,2,3, but also a critical issue in a number of quantum technologies including spin-based quantum information processing4,5 and ultrasensitive magnetometry6,7,8,9,10. For example, decoherence from the environmental spin bath is often a limiting factor when using systems such as phosphorous donors in silicon11,12,13,14,15,16, semiconductor quantum dots17,18 and nitrogen vacancy centres in diamond19,20, as quantum bits or sensors. Studying central spin decoherence caused by environmental fluctuations or elementary excitations may yield key insights into the nature of many-body interactions in the environment. Furthermore, dynamical control over the central spin can affect the dynamics of the environment in a detectable manner8,18, even to the extent of coherently controlling21,22 or dynamically polarizing nuclear spin baths23,24. In the light of these ideas, exploiting central spin decoherence for sensing single-nuclear spins or nuclear spin clusters in spin baths has been theoretically proposed6,7,8 and experimentally demonstrated9,10. Recently, this idea has been pushed to new depths: theoretical studies show that the central spin decoherence can be a novel probe to many-body physics, in particular, phase transitions in spin baths25,26,27,28. Multiple-spin correlations are one of the essential characteristics in spin baths11,12,13,14,15,16,17,18,19,20, but detection of such correlations is a long-standing challenge in many-body physics. Here we address this problem with the first experimental demonstration of detection of many-body correlations via central spin decoherence, laying a foundation for studying many-body physics and phase transitions in spin baths25,26,27,28.
Previous approaches to studying multiple-particle correlations include the use of nonlinear optical spectroscopy of excitons in semiconductors29,30,31,32, nuclear magnetic resonance (NMR) spectroscopy of nuclear spins in molecules33, and the generalization of multi-dimensional NMR to optical spectroscopy34,35. Nevertheless, the detection and characterization of many-body correlations in nanoscale systems36,37 remain highly challenging due to the weak signals in such small systems.
In this article, taking a phosphorus donor electron spin in a natural-abundance 29Si nuclear spin bath as our model system, we show both theoretically and experimentally that many-body correlations in nanoscale nuclear spin baths produce identifiable signatures in the decoherence of the central spin under multiple-pulse dynamical decoupling (DD) control. The DD control over the central spin establishes and manipulates correlations among the nuclear spins in the bath. When the number of decoupling π-pulses is odd, central spin decoherence is primarily driven by second-order nuclear spin correlations (pairwise flip-flop processes). In contrast, when the number of π-pulses is even, fourth-order nuclear spin correlations (diagonal interaction renormalized pairwise flip-flop processes) are principally responsible for the central spin decoherence. Our method is particularly suited for the detection of many-body correlations in nanoscale systems.
Results
System and model
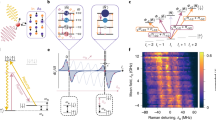
We consider the electron spin (S=1/2) of a phosphorus donor localized in silicon as the central spin (Fig. 1a). This donor electron spin is coupled with a 29Si nuclear spin bath (I=1/2 and natural abundance of 4.7% throughout the host lattice) by the contact hyperfine interactions and dipolar interactions14. In a strong external magnetic field (>100 mT), the Zeeman energies of the donor spin and nuclear spins are conserved, so the total spin Hamiltonian can be written in the secular form12,13
(a) Due to the extended donor wavefunction, the P-donor electron spin (blue arrow) interacts with a bath of 29Si nuclear spins (magenta arrows) possessing various many-body correlations. (b) Topologically inequivalent connected diagrams (LCE diagrams) corresponding to different many-body correlations in the nuclear spin bath: (I) V2—second-order pairwise flip-flop diagram, (II–V) V4z—fourth-order diagonal interaction renormalized pairwise flip-flop diagrams. Here the nuclear spin operators  are represented in turn by filled circles, empty circles or empty squares. The off-diagonal (diagonal) interaction terms are represented by wavy (dashed) lines. The solid arrows represent nuclear spin correlation functions between
are represented in turn by filled circles, empty circles or empty squares. The off-diagonal (diagonal) interaction terms are represented by wavy (dashed) lines. The solid arrows represent nuclear spin correlation functions between  and
and  (or
(or  ) with the arrows indicating the direction of time propagation.
) with the arrows indicating the direction of time propagation.

where ωe/n=γe/nB is the Larmor frequency of the donor electron spin /bath nuclear spins, γe/n is the gyromagnetic ratio of the donor electron spin /bath nuclear spins, and B is the external magnetic field applied along the z axis. The coupling coefficient between the donor spin and the ith nuclear spin is Ai=γeγn{8π/3|ψ(Ri)|2+∫d3r|ψ(r)|2[3(rz–Riz)2–|r–Ri|2]/|r–Ri|5}, where the first term is the Fermi contact interaction given by the donor electron density |ψ(Ri)|2 at the position of the ith nuclear spin14 and the second term is the dipolar interaction. The donor electron density decays exponentially with r, while the dipolor interaction decays with distance by r−3, such that the dipolar interaction starts contributing only for |Ri|>r0=2 nm. It can therefore be approximated as γeγnθ(|Ri|–r0)(3cos2θi–1)/|Ri|3, where θ(r) is the Heaviside step function and θi is the angle between the nuclear spin position vector Ri and the magnetic field vector B. The dipolar interaction between the nuclear spins is Dij=γn2(3cos2θij–1)/4|Rij|3, where θij is the angle between Rij=Ri–Rj and B.
We assume that the donor electron spin is initially prepared in the coherent state  by a π/2 rotation (with +/− being spin-up/down along the magnetic field direction). In the subsequent evolution, the central spin suffers decoherence as a result of its coupling to the nuclear spin bath. However, by applying DD control38,39 to the central spin (consisting of a sequence of π-flips at times {t1,t2⋯tn}), we can reduce its sensitivity to the bath in general while selectively enhancing the effect of certain multiple-spin dynamics8. With DD, the restored central spin coherence following a total evolution time T is
by a π/2 rotation (with +/− being spin-up/down along the magnetic field direction). In the subsequent evolution, the central spin suffers decoherence as a result of its coupling to the nuclear spin bath. However, by applying DD control38,39 to the central spin (consisting of a sequence of π-flips at times {t1,t2⋯tn}), we can reduce its sensitivity to the bath in general while selectively enhancing the effect of certain multiple-spin dynamics8. With DD, the restored central spin coherence following a total evolution time T is

with PJ being the probability of the nuclear state |J› and

where H0=(1/2)∑iAiIiz and V=∑i<jDij(Ii+Ij−+Ii−Ij+–4IizIjz). Here, the nuclear Zeeman term ωn∑iIiz is dropped since it has no contribution to the spin decoherence. The nuclear spin bath is assumed to be in an infinite-temperature (fully mixed) state (PJ=1/2M) with density matrix  , where |J› is an eigenstate of ∑iIiz and M being the number of nuclear spins in the bath.
, where |J› is an eigenstate of ∑iIiz and M being the number of nuclear spins in the bath.
We consider two families of DD sequences: Carr–Purcell–Meiboom–Gill (CPMG)40,41,42 and Uhrig DD (UDD)43,44 (Fig. 2a). An n-pulse CPMG sequence periodically flips the central spin at time tc=(2c–1)T/2n, while n-pulse UDD flips the central spin at time tc=Tsin2[cπ/(2n+2)], where T is the total evolution time and c=1, 2,⋯, n. It should be noted that CPMG and UDD are equivalent for n≤2, and for n=1 simply correspond to the Hahn echo.
(a) Schematics of various CPMG and UDD pulse sequences. (b) Comparisons of the P-donor electron spin decoherence in a natural abundance 29Si nuclear spin bath calculated by the numerically exact CCE method (lines) and those by the LCE approximation (symbols) to determine the many-body correlations that contribute significantly to the spin decoherence under various CPMG and UDD controls. Here, LCE-V2 (crosses) represents the leading-order pairwise flip-flop processes in the nuclear spin bath which dominate for sequences with an odd number of π pulses, while LCE-V4z (squares) represents the diagonal interaction renormalized pairwise flip-flop processes which dominate for the even-numbered sequences where LCE-V2 is zero (see Fig. 1b). The magnetic field was set as B=0.3 T applied along the [110] lattice direction.
Many-body correlation effects on central spin decoherence
According to the linked-cluster expansion (LCE) theorem in many-body physics45, the quantum evolution of a nuclear spin bath from an initial state |J› can be factorized into contributions of different orders of irreducible many-body correlations, namely,

with the lth order many-body correlation

where  is the time-ordering operator along the contour C(0→T→0), and V(t)=exp(iH0t)V exp(−iH0t) is the intra-bath coupling in the interaction picture. Note that the hyperfine interaction H0 enters into the time evolution of the bath correlations. We show some examples of the expansion terms diagrammatically in Fig. 1b (see Methods for calculation of the diagrams). Here we assume the nuclear spin bath starts from a pure product state |J›. The thermal ensemble results can be obtained by sampling over different initial states and then taking a statistical average.
is the time-ordering operator along the contour C(0→T→0), and V(t)=exp(iH0t)V exp(−iH0t) is the intra-bath coupling in the interaction picture. Note that the hyperfine interaction H0 enters into the time evolution of the bath correlations. We show some examples of the expansion terms diagrammatically in Fig. 1b (see Methods for calculation of the diagrams). Here we assume the nuclear spin bath starts from a pure product state |J›. The thermal ensemble results can be obtained by sampling over different initial states and then taking a statistical average.
For each LCE term, the real part contributes to the spin decoherence while the imaginary part just produces a coherent phase shift (corresponding to self-energy renormalization of the probe spin). Under CPMG-n or UDD-n control, the first-order LCE term (l=1) vanishes due to the contour integral. The second-order LCE term (l=2) corresponds to the leading-order pairwise flip-flop processes in the nuclear spin bath, in which the bath dynamics is approximated as a product of evolutions of nuclear spin pairs15,17,18. Previous studies identified this term as the main cause of spin decoherence for the free-induction decay and Hahn echo in the strong magnetic field regime15,17,18. The pairwise flip-flop processes of nuclear spins i, j can be mapped to the precession of a pseudospin σij about a pseudofield =(Dij, 0, ±ωij/2) conditioned on the central spin state |±› (ref. 17), where ωij=(Ai−Aj)/2 is the energy cost of the flip-flop process (see ‘Pseudospin model’ in Methods for details). If the central spin is under CPMG-n control, we have  when n is odd, but
when n is odd, but  when n is even (see the schematics in Fig. 3a), where t=T/2n. For UDD-n control, the real part of the second-order LCE term also vanishes when n is even and is non-zero when n is odd (see ‘Derivation of LCE terms’ in Methods for details).
when n is even (see the schematics in Fig. 3a), where t=T/2n. For UDD-n control, the real part of the second-order LCE term also vanishes when n is even and is non-zero when n is odd (see ‘Derivation of LCE terms’ in Methods for details).
(a) Schematics of bifurcated pseudospin evolutions conditioned on the central spin state under CPMG-2 (or UDD-2) control. The conjugate pseudospins  (corresponding to the central spin in the state |±›) describe the dynamics of two-spin correlations. The more the trajectories are separated, the greater the central spin decoherence. The conjugate pseudospins exchange their pseudofields
(corresponding to the central spin in the state |±›) describe the dynamics of two-spin correlations. The more the trajectories are separated, the greater the central spin decoherence. The conjugate pseudospins exchange their pseudofields  at time t=τ, 3τ when the central spin is flipped by a π-pulse. Without the diagonal interaction renormalization, the conjugate trajectories are symmetric and coincide at time T in the leading order of the evolution time, leading to cancellation of decoherence. (b) Histogram of the number of nuclear spin clusters (with inter-nuclei distances <1 nm) in 200 different bath configurations. (c) Decomposition of the LCE-V4z term into three-body and four-body correlations (see Fig. 1a) for CPMG-2 (or UDD-2) control of the central spin. The magnetic field was B=0.3 T applied along the [110] lattice direction.
at time t=τ, 3τ when the central spin is flipped by a π-pulse. Without the diagonal interaction renormalization, the conjugate trajectories are symmetric and coincide at time T in the leading order of the evolution time, leading to cancellation of decoherence. (b) Histogram of the number of nuclear spin clusters (with inter-nuclei distances <1 nm) in 200 different bath configurations. (c) Decomposition of the LCE-V4z term into three-body and four-body correlations (see Fig. 1a) for CPMG-2 (or UDD-2) control of the central spin. The magnetic field was B=0.3 T applied along the [110] lattice direction.
For higher order LCE terms, there are three groups of diagrams: ring diagrams, diagonal-interaction renormalized diagrams and locked diagrams45. Generally, the leading terms of the lth order diagrams are proportional to (Dij/ωij)l. Due to the random distribution of nuclear spins, the contributions from different nuclear spin clusters add destructively when l is odd but add constructively when l is even. Hence, the odd-order LCE terms contribute negligibly to the spin decoherence.
The central spin decoherence problem can be exactly solved by the cluster-correlation expansion (CCE) method46. To identify the contributions of different many-body correlations to the central spin decoherence, we compare the approximate results obtained by the LCE to the exact numerical results obtained by the CCE (Fig. 2b). We see that the second-order pairwise flip-flop LCE term (V2) almost fully reproduces the CCE results for DD controls of odd pulse number, while the contribution of the fourth-order diagonal-interaction renormalized LCE term (V4z) coincides with the CCE results for DD controls of even pulse number. This indicates that we can selectively detect either the second-order or fourth-order many-body correlations by choosing an appropriate number of DD control pulses. Similar pulse-number parity effects were theoretically noticed before42, however, without analysing the underlying microscopic processes.
The different correlations actually present different central spin decoherence features. In particular, the V2 correlation causes decoherence with a faster initial decay but a longer decay tail ( ); while the decoherence induced by the V4z correlation is better preserved in the short time regime but decays faster in the long time regime (
); while the decoherence induced by the V4z correlation is better preserved in the short time regime but decays faster in the long time regime ( ).
).
It should be pointed out that the LCE-V4z term contains two-body, three-body and four-body nuclear spin correlations (Fig. 1b). The two-body V4z correlations have no contribution to decoherence, because the pairwise flip-flop of two nuclear spins is independent of the diagonal interaction between them. The nuclear spin clusters contributing the most to central spin decoherence are those four-spin or three-spin clusters with small inter-nuclei distances (<1 nm), so that the energy cost of the pairwise flip-flop processes of two nuclear spins is significantly changed by the other nuclear spins in the cluster (see ‘Pseudospin model’ in Methods for details). The typical strength of the interaction between nuclear spins in such clusters is ~100 Hz, which is in the same order of the NMR linewidth of 29Si in natural silicon samples23. In the calculations, we consider a bath volume with radius 8 nm from the central spin, corresponding to 5,000 nuclear spins. Statistical studies (Fig. 3b) show that there are about 1.8 × 104 such four-spin clusters and 2.6 × 104 three-spin clusters in the bath. In Fig. 3c, we compare the contributions of different many-body correlations and find that the four-body correlations are the main contribution to the central spin decoherence under DD control of even number of pulses. The three-body correlations are non-zero but relatively small.
Experimental results
We have observed the pulse-number parity effect in DD experiments on P-donors in natural Si (Fig. 4). The measured decoherence decays fit well in stretched exponential functions  (see Supplementary Fig. 1). Here the first term
(see Supplementary Fig. 1). Here the first term  represents the instantaneous diffusion caused by dipolar coupling to other P-donor electron spins in the sample ([P]=3 × 1014 per cm3), and the second term
represents the instantaneous diffusion caused by dipolar coupling to other P-donor electron spins in the sample ([P]=3 × 1014 per cm3), and the second term represents the central spin decoherence (spectral diffusion) caused by the 29Si nuclear spin bath.
represents the central spin decoherence (spectral diffusion) caused by the 29Si nuclear spin bath.
(a,b) Measured (solid lines) and calculated (dashed lines) coherence of the P-donor electron spin in the natural 29Si nuclear spin bath under (a) CPMG or (b) UDD control. We attribute the deviation seen at ~1 ms for CPMG-6 to an overlap with uncorrected stimulated/unwanted echoes. (c,d) Comparisons of the experimental (solid lines) and theoretical (dashed line) decay times τSD (blue) and stretched exponents λ (magenta) of the central spin decoherence under (c) CPMG or (d) UDD control. The error bars correspond to the systematic errors of the stretched exponential fitting of the plots in a,b. The magnetic field was B=0.3 T applied along the [110] lattice direction.
In Fig. 4a,b, we show the measured decays, corrected to exclude the instantaneous diffusion (with τID=10 ms determined by the initial exponential decay of the raw experimental data in Supplementary Fig. 1). The measured and calculated results agree well for both CPMG-n and UDD-n controls, without any adjustable parameters in the calculations. In Fig. 4c,d, we compare the central spin coherence decay time τSD and exponent stretching factor λ of the measured and numerical data as functions of the pulse number n. The quantitative and qualitative agreement is remarkable, the only exception being that the measured decay time τSD oscillates with n somewhat less strongly than expected. As predicted, the stretching factor λ oscillates between about 2 and 4 as n increases, meaning that either the second-order correlations or fourth-order correlations contribute dominantly to central spin decoherence. The slight decrease of the stretched exponent λ with n can be ascribed to the emergence of the ‘Markovian’ decoherence when the coherence time is prolonged to exceed the pairwise flip-flop time and the higher order many-body correlations become more important46.
Discussion
The different signatures of the many-body correlations under DD control of the central spin, in particular the pulse-number parity effect in the number of DD control pulses, provide a useful approach to studying many-body physics in the nuclear spin bath. Note that the parity effect is not affected by the type of DD sequences adopted in this paper—it exists in both CPMG and UDD controls. It is remarkable that the many-body correlations between nuclear spins have sizable effects even at temperatures (a few Kelvin in our experiments) much higher than the coupling strengths between the nuclear spins (a few nano-Kelvin).
The pulse-number parity effect should be observable in a broad range of central spin systems as long as the following conditions are satisfied: (i) pure dephasing condition—the external magnetic field should be large so that the energy non-conserving processes (such as single-nuclear spin rotations) are highly suppressed (that is, the total Hamiltonian can be written in the secular form); (ii) slow/non-Markovian bath condition—the decoherence time should be much shorter than the nuclear spin cluster correlation times (so that the LCE terms converge rapidly with increasing orders and the central spin decoherence is mainly induced by the lowest-order non-zero LCE terms). Extending the study of nuclear spin correlation effects to other types of shallow donors in semiconductors (such as bismuth donors in silicon47,48) would be quite straightforward. It is also possible to observe similar effects for electron spins in semiconductor quantum dots (such as GaAs and InAs quantum dots17,18,42) under the conditions that a strong magnetic field (>100 mT) is applied and DD control is available. On the other hand, deep centres like nitrogen vacancy centres in diamond are not likely to produce the pulse-parity effect, since in such systems, the electron spins interact with only a small number of nuclear spins (~100) through the (rapidly decaying) dipolar interaction and the decoherence time becomes comparable with the nuclear spin cluster correlation time. This makes the higher order LCE terms (compared with V2 and V4z) contribute significantly to decoherence for both odd and even pulse numbers.
The detection of many-body correlations may find applications in identifying the structures of molecules and defect complexes in solids. For example, the pulse-number parity effect can be adopted to tell whether the molecules/defects that form the nuclear spin bath have two-body or higher order interactions among the nuclei. The delocalized nature of the electron spin in many molecules49 makes it interact with a large number of nuclear spins and therefore lends itself to such an approach.
It should be noted that the current scheme can only detect up to the fourth order (four-body) correlations. Generalization to detection of higher order correlations is in principle possible by using more complicated dynamical control (in timing, composition, and so on) and/or different types of probes (for example, higher spins). Exploration along this line will provide interesting topics for future studies.
Methods
Interaction picture
The propagators of the nuclear spin bath can be written as45


where  is the time-ordering operator and
is the time-ordering operator and

with  and ωi=Ai/2. By the relations above, the operator
and ωi=Ai/2. By the relations above, the operator  can be rewritten in the interaction picture as the product of several evolution operators. For example, for the CPMG-1 (UDD-1) and CPMG-2 (UDD-2) controls
can be rewritten in the interaction picture as the product of several evolution operators. For example, for the CPMG-1 (UDD-1) and CPMG-2 (UDD-2) controls


with t=T/(2n).
Generalized Wick’s theorem for spin 1/2
Wick’s theorem for bosons or fermions cannot be directly used for the nuclear spins, because the commutation brackets of spin operators do not yield c-numbers. Previous studies generalized Wick’s theorem to spin 1/2 operators45,50. First, we define the contraction of two spin operators as

where  is the normal ordered operator depending on the state of the nuclear spin
is the normal ordered operator depending on the state of the nuclear spin  such that
such that  . For example,
. For example,


If the ith nuclear spin is in the spin-down state ( ), we have the following contraction relations50
), we have the following contraction relations50

where θ(t) is the Heaviside step function. If  , we can get the new contraction relations from equation (11) by the transformation
, we can get the new contraction relations from equation (11) by the transformation  and with the right side of the equations changing the signs.
and with the right side of the equations changing the signs.
Now we can state the generalized Wick’s theorem for spin 1/2 operators: the time-ordered product of a set of time-dependent spin operators is equal to the sum of all possible fully contracted products which contains only  operators45,50.
operators45,50.
Derivation of LCE terms
Now we can derive the analytical forms of the LCE terms. First we calculate the LCE-V1 term (Fig. 5a),
(a) V1—first-order diagram, (b) V2—second-order pairwise flip-flop diagram, (c,d) V3z—third-order diagonal interaction renormalized pairwise flip-flop diagrams, (e) V3r—third-order ring diagram, (f) V4r—fourth-order ring diagram, (g–j) V4z—fourth-order diagonal interaction renormalized pairwise flip-flop diagrams, (k,l) V4l—fourth-order locked diagrams.(m,n) V4rz—fourth-order diagonal interaction renormalized ring diagrams.

where  and
and  . We see that this term vanishes due to the contour integral. The LCE-V2 term (Fig. 5b) is
. We see that this term vanishes due to the contour integral. The LCE-V2 term (Fig. 5b) is

For the CPMG-n control, we have  when n is odd, and Re‹V2›=0 when n is even. For the UDD-n control, we also have Re‹V2›=0 when n is even, but Re‹V2› cannot be written in a simple compact form as in the CPMG case when n is odd (n>2).
when n is odd, and Re‹V2›=0 when n is even. For the UDD-n control, we also have Re‹V2›=0 when n is even, but Re‹V2› cannot be written in a simple compact form as in the CPMG case when n is odd (n>2).
The LCE-V4z term includes four diagrams (Fig. 5g–j). However, the last two diagrams (Fig. 5i,j) have no contribution to central spin decoherence, because the pairwise flip-flop processes of nuclear spins (i, j) are independent of the diagonal interactions between them ( ) (so the fourth order terms in Fig. 5i,j approximately reduce to the same form as in Fig. 5c,d, respectively, but are higher order small quantities). Therefore the pairwise dynamics (Fig. 6a) is well approximated by the diagram in Fig. 5b. For the diagrams in Fig. 5g,h, we can get analytical results of the three-body and four-body correlations for the CPMG and UDD control of even pulse number as follows
) (so the fourth order terms in Fig. 5i,j approximately reduce to the same form as in Fig. 5c,d, respectively, but are higher order small quantities). Therefore the pairwise dynamics (Fig. 6a) is well approximated by the diagram in Fig. 5b. For the diagrams in Fig. 5g,h, we can get analytical results of the three-body and four-body correlations for the CPMG and UDD control of even pulse number as follows
We only consider the V2 and V4z terms contributing most to central spin decoherence. The fourth-order diagonal-interaction renormalized pair flip-flop processes (V4z) can be two-body, three-body or four-body correlations. The two-body correlations describe the pairwise flip-flop processes of nuclear spins i, j renormalized by the diagonal couplings between i and j, while the three-body (four-body) correlations describe the pairwise flip-flop processes of nuclear spins i, j renormalized by the diagonal couplings of i, j to nuclear spin k (k, l) in the nuclear spin bath. Note that in this figure, the vertices along the same horizontal line are of the same spin.

where Lijk and Lijkl denote the central spin decoherence caused by the diagonal interaction renormalized pairwise flip-flop processes (i↔j) in the three-spin cluster {i,j,k} (Fig. 6b) and four-spin clusters {i,j,k,l} (Fig. 6c), respectively, and  . These analytical expressions imply that to have significant contributions to the central spin decoherence, the nuclear spin clusters should satisfy the following conditions: (i) the inter-nuclei distances in four-spin clusters or three-spin clusters should be rather small (<1 nm); (ii) the renormalization to the energy cost of the pair flip-flop (i, j) should be substantial as compared with the bare energy cost, that is,
. These analytical expressions imply that to have significant contributions to the central spin decoherence, the nuclear spin clusters should satisfy the following conditions: (i) the inter-nuclei distances in four-spin clusters or three-spin clusters should be rather small (<1 nm); (ii) the renormalization to the energy cost of the pair flip-flop (i, j) should be substantial as compared with the bare energy cost, that is,  should be large for three-spin clusters {i,j,k} while
should be large for three-spin clusters {i,j,k} while  should be positive and large for four-spin clusters{i,j,k,l}.
should be positive and large for four-spin clusters{i,j,k,l}.
Pseudospin model
To get an intuitive understanding of the pulse-number parity effect, we use the pseudospin model17 to describe the dynamics of two nuclear spins. In the strong field regime, the Hamiltonian of the ith and jth nuclear spins conditioned on the central spin state

where the basis set is defined as . Note that the two pseudofields corresponding to the two opposite central spin states lie in the xz plane and are symmetric with respect to the x axis. The time evolution operator is
. Note that the two pseudofields corresponding to the two opposite central spin states lie in the xz plane and are symmetric with respect to the x axis. The time evolution operator is

Where φ=κt,  ,
,  ,
,  . If the central spin is under CPMG-n or UDD-n control, the time evolution operator
. If the central spin is under CPMG-n or UDD-n control, the time evolution operator  can be obtained by the above formula. For CPMG-1 (UDD-1) and CPMG-2 (UDD-2) controls, we have
can be obtained by the above formula. For CPMG-1 (UDD-1) and CPMG-2 (UDD-2) controls, we have

For the donor spin in silicon, we have ωij≫Dij, so nx≈2Dij/ωij is a small quantity. The difference between  and
and  causes the central spin decoherence
causes the central spin decoherence  . When n=2k+1, we have
. When n=2k+1, we have  and
and  . However, when n=2k, due to the symmetry between the two pseudofields corresponding to the two opposite central spin states, the two conjugate trajectories of the pseudospin under the two pseudofields cross into each other (in the leading order of evolution time) at the end of the DD control. Therefore
. However, when n=2k, due to the symmetry between the two pseudofields corresponding to the two opposite central spin states, the two conjugate trajectories of the pseudospin under the two pseudofields cross into each other (in the leading order of evolution time) at the end of the DD control. Therefore  and
and  . Here fn(T) is a function of the total evolution time T and the pulse number of DD control n.
. Here fn(T) is a function of the total evolution time T and the pulse number of DD control n.
If we consider all the nuclear spins in the bath, then the central spin decoherence can be expressed as the product of the decoherence contributed by each pair of nuclear spins. Then we have


These results are consistent with results obtained by the LCE method. Recall that the LCE-Vl terms are proportional to (Dij/ωij)l. Therefore, for CPMG or UDD control of odd pulse numbers, the second-order correlations contribute the most to the central spin decoherence. But for the CPMG or UDD control of even pulse numbers, the second-order correlations are cancelled and the fourth-order correlations corresponding to the ring diagrams V4r and locked diagrams V4l (Fig. 5) would contribute the most to the central spin decoherence. It should be pointed out that in the discussion above, we have not considered the diagonal interactions between the nuclear spins i, j and other nuclear spins in this pseudospin model. Actually, such diagonal interactions will renormalize the pseudospin Hamiltonian and break the symmetry between the two conjugate pseudofields for the pseudospin.
The renormalization effect depends on the magnetic field direction which determines the dipolar interactions between nuclear spins (see Supplementary Fig. 2). For B//[111], the nearest neighbour nuclear spins (which contributes most to decoherence) have strong dipolar interactions, which make the pairwise flip-flop processes hard to be renormalized by other spins. But as B//[001] or [110], the nearest neighbour nuclear spins have zero or weak dipolar interactions, rendering the pairwise flip-flop processes easier to be renormalized by other spins. Therefore, when the number of pulses is even, the higher order pairwise flip-flop processes (V4l and V4r) contributes most to the central spin decoherence as B//[111], while the diagonal interaction renormalized pairwise flip-flop processes (V4z) contribute most to the central spin decoherence as B//[001] or [110].
Numerical simulation method
The P-donor electron spin decoherence in a natural abundance 29Si nuclear spin bath was numerically solved by the well-established CCE method46. We included about 5,000 nuclear spins that are located within 8 nm from the P-donor nucleus. Nuclear spins beyond this range have negligible contribution to the central spin decoherence as evidenced by the converged numerical results with increasing bath size. The central spin coherence time depends on the random configuration of 29Si nuclear spin positions in the lattice. To compare with the experimental results, we ran simulations for 100 random nuclear spin configurations and took the ensemble average of the corresponding time-domain spin coherence. Since the central spin decoherence is almost independent of the initial state of the nuclear spin bath as long as the initial state is roughly unpolarized, we just took a random unpolarized single-sample state |J› (an eigenstate of {Iiz}) as the initial state of the nuclear spin bath.
Experimental setup
Experimental results were measured on a natural silicon Czochralski wafer doped with 3 × 1014 per cm3 phosphorus, using an X-band (9.6 GHz) Bruker ELEXSYS 580 spectrometer. All decay times were obtained on the high-field electron spin resonance line (mI=−1/2) at 3,452 G at 6 K (where the electron spin relaxation processes (T1≈1 s) did not contribute to decoherence over the timescales considered in this paper). The multiple pulses required for the DD sequences can result in ‘stimulated echoes’, and other unwanted echoes, in the experiment due to pulse infidelities. When such echoes overlap with the desired one (from spin packets which have been flipped by all the π pulses), the experimentally observed decay curves gain unwanted contributions. We therefore cycled the phases of the applied π pulses in such a way as to remove the contribution of all undesired echoes. For UDD, the timings between each pulse are different and most stimulated echoes fall outside the desired one which can then be isolated. For example, the phase cycling sequence for UDD-4 requires simply subtracting the echo from two experiments where the first two pulses are changed from +π to –π and the last two are +π. For CMPG, this is more challenging as the intervals are equal and we did not suppress all possible stimulated echoes for CPMG-5 and CPMG-6.
Additional information
How to cite this article: Ma, W.-L. et al. Uncovering many-body correlations in nanoscale nuclear spin baths by central spin decoherence. Nat. Commun. 5:4822 doi: 10.1038/ncomms5822 (2014).
References
Zurek, W. H. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 75, 715 (2003).
Schlosshauer, M. Decoherence, the measurement problem, and interpretations of quantum mechanics. Rev. Mod. Phys. 76, 1267 (2005).
Prokof’ev, N. V. & Stamp, P. C. E. Theory of the spin bath. Rep. Prog. Phys. 63, 669 (2000).
Awschalom, D. D. et al. Quantum spintronics: engineering and manipulating atom-like spins in semiconductors. Science 339, 1174 (2013).
Ladd, T. D. et al. Quantum computers. Nature 464, 45 (2010).
Hall, L. T. et al. Monitoring ion-channel function in real time through quantum decoherence. Proc. Natl Acad. Sci. USA 107, 18777–18782 (2010).
Hall, L. T. et al. Ultrasensitive diamond magnetometry using optimal dynamic decoupling. Phys. Rev. B 82, 045208 (2010).
Zhao, N., Hu, J. -L., Ho, S. -W., Wan, J. T. K. & Liu, R. B. Atomic-scale magnetometry of distant nuclear spin clusters via nitrogen-vacancy spin indiamond. Nat. Nanotech. 6, 242–246 (2011).
Zhao, N. et al. Sensing single remote nuclear spins. Nat. Nanotech. 7, 657–662 (2011).
Shi, F. Z. et al. Sensing and atomic-scale structure analysis of single nuclear-spin clusters in diamond. Nat. Phys. 10, 21–25 (2014).
Feher, G. Electron spin resonance experiments on donors in silicon. I. electronic structure of donors by the electron nuclear double resonance technique. Phys. Rev. B 114, 1219 (1959).
Witzel, W. M., Carroll, M. S., Morello, A., Cywin´ski, Ł. & Das Sarma, S. Electron spin decoherence in isotope-enriched silicon. Phys. Rev. Lett. 105, 187602 (2010).
Tyryshkin, A. M., Lyon, S. A., Astashkin, A. V. & Raitsimring, A. M. Electron spin relaxation times of phosphorus donors in silicon. Phys. Rev. B 68, 193207 (2003).
de Sousa, R. & Das Sarma, S. Theory of nuclear-induced spectral diffusion: spin decoherence of phosphorus donors in Si and GaAs quantum dots. Phys. Rev. B 68, 115322 (2003).
Witzel, W. M. & Das Sarma, S. Quantum theory for electron spin decoherence induced by nuclear spin dynamics in semiconductor quantum computer architectures: spectral diffusion of localized electron spins in the nuclear solid-state environment. Phys. Rev. B 74, 035322 (2003).
Morton, J. J. L., McCamey, D. R., Eriksson, M. A. & Lyon, S. A. Embracing the quantum limit in silicon computing. Nature 464, 345–353 (2011).
Yao, W., Liu, R. -B. & Sham, L. J. Theory of electron spin decoherence by interacting nuclear spins in a quantum dot. Phys. Rev. B 74, 195301 (2006).
Liu, R. -B., Yao, W. & Sham, L. J. Control of electron spin decoherence caused by electron–nuclear spin dynamics in a quantum dot. New J. Phys. 9, 226 (2007).
Gruber, A. et al. Scanning confocal optical microscopy and magnetic resonance on single defect centers. Science 276, 2012–2014 (1997).
Zhao, N., Ho, S.-W. & Liu, R.-B. Decoherence and dynamical decoupling control of nitrogen vacancy center electron spins in nuclear spin baths. Phys. Rev. B 85, 115303 (2012).
Zhao, N., Wang, Z.-Y. & Liu, R.-B. Anomalous decoherence effect in a quantum bath. Phys. Rev. Lett. 106, 217205 (2011).
Huang, P. et al. Observation of an anomalous decoherence effect in a quantum bath at room temperature. Nat. Commun. 2, 570 (2011).
Hayashi, H. et al. Dynamic nuclear polarization of 29Si nuclei in isotopically controlled phosphorus doped silicon. Phys. Rev. B 80, 045201 (2009).
Itahashi, T. et al. Optical and dynamic nuclear polarization of 29Si nuclei via photoexcited triplet states of oxygen-vacancy complexes in isotopically controlled silicon. Phys. Rev. B 87, 075201 (2013).
Quan, H. T., Song, Z., Liu, X. F., Zanardi, P. & Sun, C. P. Decay of loschmidt echo enhanced by quantum criticality. Phys. Rev. Lett. 96, 140604 (2006).
Wei, B.-B. & Liu, R.-B. Lee-Yang zeros and critical times in decoherence of a probe spin coupled to a bath. Phys. Rev. Lett. 109, 185701 (2012).
Chen, S.-W., Jiang, Z.-F. & Liu, R.-B. Quantum criticality at high temperature revealed by spin echo. New J. Phys. 15, 043032 (2013).
Cai, J., Retzker, A., Jelezko, F. & Plenio, M. B. A large-scale quantum simulator on a diamond surface at room temperature. Nat. Phys. 9, 168–173 (2013).
Chemla, D. S. & Shah, J. Many-body and correlation effects in semiconductors. Nature 411, 549–557 (2001).
Östreich, Th., Schönhammer, K. & Sham, L. J. Exciton-exciton correlation in the nonlinear optical regime. Phys. Rev. Lett. 74, 4698 (1995).
Bolton, S. R., Neukirch, U., Sham, L. J., Chemla, D. S. & Axt, V. M. Demonstration of sixth-order Coulomb correlations in a semiconductor single quantum well. Phys. Rev. Lett. 85, 2002 (2000).
Turner, D. B. & Nelson, K. A. Coherent measurements of high-order electronic correlations in quantum wells. Nature 466, 1089–1092 (2010).
Ernst, R. R., Bodenhausen, G. & Wokaun, A. Principles of Nuclear Magnetic Resonance in One and Two Dimensions Oxford Univ. Press (1990).
Brixner, T. et al. Two-dimensional spectroscopy of electronic couplings in photosynthesis. Nature 434, 625–628 (2005).
Li, X., Zhang, T., Borca, C. N. & Cundiff, S. T. Many-body interactions in semiconductors probed by optical two-dimensional fourier transform spectroscopy. Phys. Rev. Lett. 96, 057406 (2006).
Bader, S. D. Colloquium: opportunities in nanomagnetism. Rev. Mod. Phys. 78, 1–15 (2006).
Kane, B. E. A silicon-based nuclear spin quantum computer. Nature 434, 625–628 (2005).
Viola, L., Knill, E. & Lloyd, S. Dynamical decoupling of open quantum systems. Phys. Rev. Lett. 82, 2417 (1998).
de Lange, G., Wang, Z. H., Ristè, D., Dobrovitski, V. V. & Hanson, R. Universal dynamical decoupling of a single solid-state spin from a spin bath. Science 330, 60–63 (2010).
Carr, H. Y. & Purcell, E. M. Effects of diffusion on free precession in nuclear magnetic resonance experiments. Phys. Rev. 94, 630 (1954).
Meiboom, S. & Gill, D. Modified spin-echo method for measuring nuclear relaxation times. Rev. Sci. Instrum. 29, 688 (1958).
Witzel, W. M. & Das Sarma, S. Multiple-pulse coherence enhancement of solid state spin qubits. Phys. Rev. Lett. 98, 077601 (2007).
Uhrig, G. S. Keeping a quantum bit alive by optimized π-pulse sequences. Phys. Rev. Lett. 98, 100504 (2007).
Yang, W. & Liu, R.-B. Universality of Uhrig dynamical decoupling for suppressing qubit pure dephasing and relaxation. Phys. Rev. Lett. 101, 180403 (2008).
Saikin, S. K., Yao, W. & Sham, L. J. Single-electron spin decoherence by nuclear spin bath- Linked-cluster expansion approach. Phys. Rev. B 75, 125314 (2007).
Yang, W. & Liu, R.-B. Quantum many-body theory of qubit decoherence in a finite-size spin bath. Phys. Rev. B 78, 085315 (2008).
Wolfowicz, G. et al. Decoherence mechanisms of 209Bi donor electron spins in isotopically pure 28Si. Phys. Rev. B 86, 245301 (2012).
Wolfowicz, G. et al. Atomic clock transitions in silicon-based spin qubits. Nat. Nanotech. 8, 561–564 (2013).
Du, J. et al. Preserving spin coherence in solids by optimal dynamical decoupling. Nature 461, 1265–1268 (2009).
Giovannini, B. & Koide, S. Perturbation theory for magnetic impurities in metals. Prog. Theor. Phys. 34, 705–725 (1965).
Acknowledgements
We thank I. Tchernov for his contributions to the experimental design and T. Monteiro for comments on the manuscript. This work was supported by Hong Kong RGC/GRF Project 401413, The Chinese University of Hong Kong Focused Investments Scheme, National Basic Research Program of China (973 Program) Grant No. G2009CB929300, and National Natural Science Foundation of China Grant No. 61121491. Work at UCL was supported by the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013)/ERC (Grant No. 279781), and by the Engineering and Physical Sciences Research Council (EPSRC) grants EP/K025945/1 and EP/I035536/2. J.J.L.M. is supported by the Royal Society.
Author information
Authors and Affiliations
Contributions
R.-B.L. conceived the idea. W.-L.M. and N.Z. performed the theoretical study, G.W. and J.J.L.M. carried out the experimental study. W.-L.M., G.W. and R.-B.L. wrote the paper. S.-S.L. discussed the scheme and the results. All authors analysed the results and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-2 (PDF 253 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/
About this article
Cite this article
Ma, WL., Wolfowicz, G., Zhao, N. et al. Uncovering many-body correlations in nanoscale nuclear spin baths by central spin decoherence. Nat Commun 5, 4822 (2014). https://doi.org/10.1038/ncomms5822
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms5822
This article is cited by
-
Local-Field Corrections as a Regularization Method for the Spin-Boson Model
Scientific Reports (2019)
-
Spectral hole burning and its application in microwave photonics
Nature Photonics (2017)
-
Quantum decoherence dynamics of divacancy spins in silicon carbide
Nature Communications (2016)
-
Nuclear spins get a comb-over
Nature Physics (2016)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.