Abstract
Magnetic reconnection, in which magnetic field lines break and reconnect to change their topology, occurs throughout the universe. The essential feature of reconnection is that it energizes plasma particles by converting magnetic energy. Despite the long history of reconnection research, how this energy conversion occurs remains a major unresolved problem in plasma physics. Here we report that the energy conversion in a laboratory reconnection layer occurs in a much larger region than previously considered. The mechanisms for energizing plasma particles in the reconnection layer are identified, and a quantitative inventory of the converted energy is presented for the first time in a well-defined reconnection layer; 50% of the magnetic energy is converted to particle energy, 2/3 of which transferred to ions and 1/3 to electrons. Our results are compared with simulations and space measurements, for a key step towards resolving one of the most important problems in plasma physics.
Similar content being viewed by others
Introduction
Magnetic reconnection, the breaking and topological rearrangement of magnetic field lines in plasma, occurs everywhere in the universe, in solar flares, the Earth's magnetosphere, star formation and laboratory fusion plasmas1,2,3,4. The most important feature of magnetic reconnection is that significant acceleration and heating of plasma particles occurs at the expense of magnetic energy. An example of this efficient energy conversion is the observation of large amounts of high-energy electrons associated with the reconnection of magnetic field lines in solar flares5. In the reconnection region of the Earth’s magnetosphere and the solar wind, convective outflows have been documented by in situ satellite measurements. Despite these advances, the exact physical mechanisms for bulk plasma heating, particle acceleration and energy flow channels remain unresolved. This paper addresses the key unresolved question: how is magnetic energy converted to plasma kinetic energy during reconnection? Furthermore, the conversion of magnetic energy is quantitatively evaluated for the first time in a laboratory reconnection layer by assessing the overall energy inventory in a well-defined boundary.
In the classical Sweet–Parker model1, which is based on the collision-dominated resistive magneto-hydrodynamics (MHD), the energy dissipation rate during reconnection is small (~(B2/2μ0)VA/LS(1/2)) due to the slow reconnection rate; VA is the Alfvén velocity and S (>>1) is the Lundquist number2,3,4. Observations in nearly collision-free space and laboratory plasmas show, however, that this prediction is not realized3,4. In the collisionless magnetic reconnection layer, electrons and ions move quite differently from each other due to two-fluid dynamics3,4,6,7; furthermore, differential motion between the magnetized electrons and the unmagnetized ions generates strong Hall currents in the reconnection layer. In the two-fluid formulation, the Ohm’s law of MHD should be replaced by a generalized Ohm’s law to describe the force balance of an electron flow, namely,

Here the conventional notations are used with E being the electric field and B reconnecting magnetic field, Ve the electron flow velocity, j the current density, je is the electron current density and Pe the spatially dependent electron pressure tensor3. A large out-of-plane electric field caused by the Hall currents at the reconnection layer (jHall × B) causes an increase in the reconnection rate3,4,6,7 by inducing rapid movement of the reconnecting field lines. This explains why the reconnection rate in collisionless plasmas is much faster than the classical Sweet–Parker rate.
In spite of recent progress, a major question remains unresolved: how is energy transferred from the magnetic field to plasma particles? A simple two-dimensional (2D) numerical simulation would expect that field line breaking and energy dissipation is localized in the small electron diffusion region whose width is on the order of the electron skin depth (de=c/ωpe, where c is the speed of light and ωpe is the electron plasma frequency). However, significant acceleration and heating of both ions and electrons have been observed and analyzed in a wide region of the actual reconnection layer8,9,10,11,12,13,14,15 of laboratory and space plasmas. Although quantitative studies of energy flow have been recently reported based on multiple satellite data12,15, to our knowledge, a comprehensive analysis of energy inventory over a well-defined reconnection layer has not been made. A quantitative analysis of the energy conversion rate together with the identification of heating mechanisms and location would provide key insights into the energy conversion processes.
Here we report that the energy conversion in a laboratory reconnection layer occurs in a much larger region than previously considered. We observe that electron heating occurs outside the electron diffusion region and that ion acceleration and heating dominate in a wide region of the exhaust of the reconnection layer, which ranges beyond several ion skin depths. The mechanisms for energizing plasma particles in the magnetic reconnection layer are identified, and a quantitative inventory of the converted energy is presented for the first time in a well-defined reconnection layer. The study concludes that ~50% of the magnetic energy is converted to particle energy, two-thirds of which transferred to ions and one-third to electrons. Our results are compared with numerical simulations and space measurements.
Results
Experimental apparatus
We use the MRX facility16 to experimentally study the conversion of magnetic energy to particle energy in a nearly collision-free reconnection layer. Figure 1a shows a schematic of the MRX apparatus, wherein two oppositely directed field lines merge and reconnect. Experiments are carried out in a setup in which two toroidal plasmas with annular cross-section are formed around two flux cores as shown in Fig. 1a. As we induce magnetic reconnection by driving oppositely directed field lines towards the X-point (B=0 at the centre of the layer) using pulsed flux core currents, ions and electrons also flow into the reconnection layer. The ions become demagnetized at a distance of the ion skin depth (di=c/ωpi, where ωpi is the ion plasma frequency) from the X-point where they enter the so-called ion diffusion region, and they change their trajectories and are diverted into the reconnection exhaust as seen Fig. 1b. The electrons, on the other hand, remain magnetized through the ion diffusion region and continue to flow towards the X-point. They become demagnetized only when they reach the much narrower electron diffusion region (~10de~1 cm in MRX) as seen in Fig. 1b. Electron currents flow dominantly in the out-of-plane direction (Y) near the centre (X-point) as shown in Fig.1c. For standard conditions, the electron density and temperature are, ne~(2–6) × 1013 cm−3, Te=5–15 eV, for B=0.1–0.3 kG, S >500; the electrons are well-magnetized (gyro-radius, ρe~1 mm≪plasma size, L) while the ions are not. The mean free path for electron–ion Coulomb collisions, λmfp, is in the range of 6–20 cm that is larger than the layer thickness, and as a result, the reconnection dynamics are nearly collision-free and dominated by two fluid and kinetic effects3,4. In this plasma, the energy exchange between electrons and ions is small since the characteristic energy transfer time is longer than the electron confinement time. The ion skin depth is 6–8 cm and the electron skin depth is typically 1 mm. We use (R, Y and Z) coordinates where BZ is the reconnecting field component and Y is the out-of-plane direction. Helium plasmas with a fill pressure of 4.5 mTorr are used for this study to facilitate ion temperature measurements. No external guide field is applied for this study. The plasma beta in the inflow region is about 0.1. Our measurements are carried out in a steady state reconnection phase which last 20–30 μs, significantly longer than the Alfvén time (~1 μs).
(a) MRX apparatus and the reconnection layer. Each flux core (darkened sections) contains both toroidal field (TF) and poloidal field (PF) coils. The distance between the surfaces of the two flux cores is 42 cm. After a poloidal magnetic field is created by the PF coil currents, an inductive plasma discharge is created around each flux core by pulsing the TF currents in the coils16. After the annular plasmas are created, the PF coil current can be increased or decreased to drive different modes of reconnection. For decreasing PF current, the poloidal flux in the common plasma is pulled back towards the X-point (pull mode); this mode was used for the present experiment. (b) Flow of electrons (red broken lines) and ions (blue) in the reconnection plane together with reconnecting field line components projected in the reconnection plane. The green marks are out-of-plane field component18,19. (c) Corresponding 3D schematic picture of the reconnection field lines.
We document comprehensively the dynamics of plasma particles and determine the mechanisms for energy conversion in the reconnection layer using extensive in situ diagnostics. The main diagnostic is a 2D magnetic probe array that measures the evolution of all three components of the magnetic field at >200 locations in the reconnection plane. The array consists of seven probes with a separation of 3 cm along Z. Each probe has 35 miniature pickup coils with a maximum radial (R) resolution of 6 mm. The local ion temperature is measured by an improved Ion Dynamics Spectroscopy Probe (IDSP)11,17. The line-of-sight for an inserted IDSP is typically 3 cm, which sets our spatial resolution. The ion flow vectors are measured by Mach probes. Triple Langmuir probes are used to measure electron temperature and density16. The electric field in the reconnection plane is deduced from the in-plane plasma potential profile measured by a floating potential probe and Langmuir probes11. The out-of-plane reconnection electric field is primarily inductive, which can be measured by following the movements of the reconnecting flux lines11,13.
Electron dynamics and heating in the reconnection layer
The first goal of our work is to experimentally verify the two-fluid dynamics in the reconnection region. Figure 2a depicts flow vectors of electrons in one half of the reconnection plane together with poloidal flux contours (representing magnetic field lines). The electron flow velocities (Ve) are derived from the electron current profile, which is obtained from the magnetic profile using j=∇ × B/μ0 and Ve=Vi− j/ene, where Vi is the ion flow velocity. The errors associated with the measurement of the current density are 5–10%. As conjectured by the two-fluid model, field lines moving towards the X-point (B=0 at the centre of the layer) carry electrons into the layer. The electrons remain magnetized through the ion diffusion region and continue to flow towards the X-point at the E × B drift speed. In the electron diffusion region, the magnetic field strength drops significantly, thereby driving up the in-plane electron drift speed (E/B) and injecting high-velocity electrons into the reconnection exhaust. This feature is verified in Fig. 2a,b where the measured electron inflow velocity (Ve~Vi≪VA) is much slower than the measured outflow velocity of 5–10 VA.
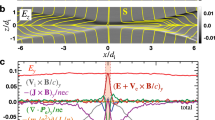
(a,b) Measured electron flow vectors and measured field lines in the half reconnection plane and its perspective view in 3D geometry. While ions and electrons move together with the field lines before entering the ion diffusion region, electrons move much faster as they approach the X-point region. Vector length (1 cm in the figure scale) stands for 4.5 × 106 cm s−1. (c,d) Strong electron temperature rise is observed in a wide area of the exhaust region, while the energy deposition to electrons, je·E, is concentrated near the X-point as seen in d: strong parallel heat conduction is considered to be the cause of the high Te at the exhaust region. The ion skin depth, di is 8 cm and the electron skin depth, de is 1 mm, typically. In this nearly collision-free condition (λmfp>>de), two-fluid dynamics dominate.
The characteristic differential flow of ions and electrons described above generates net circulating currents that flow in the reconnection plane. These currents, in turn, create an out-of-plane magnetic field with a quadrupole profile that is a signature of the Hall effect (Fig. 1b)18,19. The Hall currents also enhance the out-of-plane reconnection electric field, leading to the observed fast motion of flux lines (EY=−(1/2πR), where Ψp is the poloidal flux representing a reconnecting magnetic field flux) in the reconnection plane (that is, the measured fast rate of reconnection) as shown in equation (1)3,13. In the present work, we find a factor of 5–10 increase over the resistive term based on electron–ion Coulomb collisions.
It is verified in our experiment that the aforementioned out-of-plane Hall magnetic field has profound consequences for the 3D structure of the reconnecting field lines and of the electron flow in the reconnection layer. In particular, magnetic field lines flowing into the layer are stretched in the out-of-plane direction by the quadrupole magnetic field components (see Fig. 2b). When these stretched field lines break and reconnect at the X-point, electrons are rapidly ejected into the exhaust region with a large velocity in both the outflow (Z) and out-of-plane (Y) directions. It should be noted that this flow velocity of the electrons near the X-point is nearly orthogonal to the magnetic field lines (Fig. 2b).
A notable rise of electron temperature (up to 50%) is measured over an area that is much wider than the electron diffusion region as seen Fig 2c. The energy deposition rate on electrons, je·E, is concentrated near the X-point as seen in Fig. 2d, but in a wider region (~10de) than predicted by 2D numerical simulations20,21. The measured 2D electron temperature profile in Fig. 2c shows that the electron heating spreads along the magnetic field lines likely due to strong parallel heat conduction. Consequently, the electron temperature in the exhaust region is higher than in the inflow region. This observation agrees with the recent space observation of bulk electron heating in the reconnection exhaust region at the dayside magnetopause22. We note that Ohmic dissipation based on classical resistivity accounts for <20% of the required heating power23. Magnetic and electrostatic fluctuations in the lower hybrid frequency range (1–15 MHz) are observed23,24,25 near the X-point and throughout the downstream region, and are attributed to the observed strong electron heating, although a quantitative relationship is yet to be determined. While the magnitude of the magnetic field decreases towards the X-point, the total electron kinetic and thermal energy with respect to the magnetic energy increases substantially. The electron beta [~neTe/(B02/2μ0)] is expected to significantly exceed unity inside the observed broad electron diffusion region, breaking the condition of a magnetically confined state as is clearly seen in Fig. 2b.
Ion acceleration and heating in the reconnection layer
It is found that the flows of magnetized electrons, which cause the Hall effects, also produce a strong electric field in the reconnection plane that is strongest across the separatrices, which separates the incoming field line region from the exhaust of reconnected field lines as shown in Fig. 3a. It is experimentally verified in MRX that a saddle-shaped electric potential profile is formed in the reconnection plane to balance the Lorentz force on the electron flows11. A strong in-plane electric field is generated near the separatrices with a wider and deeper potential well downstream. The MRX potential data is consistent with measurements from the CLUSTER spacecraft8, which showed a narrow potential well near the X-point with a half width in the range of 60–100 km (3–5de), and a deeper and wider well towards the exhaust region. The in-plane electric field (or potential gradient) is largely perpendicular to the local magnetic field lines and is strongest near the separatrices20,26. The electric potential is seen to be nearly constant along a poloidal flux contour (or magnetic field line) as seen in Fig. 3a in the half reconnection plane. In this figure, we note that a large electric field across the separatrices extends to a significantly larger area of the reconnection layer (L>>di), than the region in which field line breaking and reconnection occur. A typical magnitude of the in-plane electric field, Esep is ~700 V m−1, which is much larger than the reconnection electric field in the out-of-plane direction, Erec~200 V m−1.
(a) Saddle-shaped electrostatic potential (Φp) profile deduced from Langmuir probe measurements, together with ion flow vectors (length represents velocity) measured by Mach probes. The black lines stand for the contours of the poloidal magnetic flux, Ψp. (b) the energy deposition on ions, ji·E, concentrated near the separatrices in the exhaust region. (c) Sample ion trajectories in a VPIC simulated reconnection plane with (thick solid line) and without (thick dashed line) collisions. The ion trajectories are significantly affected by the magnetic field in the downstream region through remagnetization. With collisions, ions are almost fully thermalized with a higher temperature than the initial value. (d) Normalized ion velocity (ViZ) distribution function at three different locations specified with crosses in a. The asterisks are values deduced from the measured He II 4686 Å spectra, while the solid lines stand for fitting to the Maxwellian function. Here the ion velocity is normalized by vth0, which is the ion thermal velocity in the inflow region. (e) Corresponding data from the numerical simulations are shown. The three locations are marked with crosses in c. Across the separatrix, ions are accelerated towards the outflow region. The results indicate that ion thermalization is due to remagnetization with the effects of collisions in the downstream region. We note that the ion and electron dynamics are primarily dictated by (collision free) two-fluid physics even if some energy loss mechanisms are influenced by collisions.
We observe electrostatic acceleration of ions near the separatrices due to the strong electric field mentioned above, whose spatial scale is ~2 cm, smaller than the ion gyro-radius of ~8 cm. Figure 3a also shows 2D profile of ion flow vectors measured by Mach probes, along with colour contours of the plasma potential, Φp. We observe clearly that the ion flows change their direction at the separatrices and are accelerated in both the Z and the R directions. The energy deposition rate on ions, ji·E, is concentrated near the separatrices in the exhaust region as seen in Fig. 3b. Figure 3d depicts the ion velocity distribution function versus ViZ as measured by the IDSP probes at the three locations specified in Fig. 3a. In this measurement, the IDSP spectra are converted to the local velocity distributions of ions versus ViZ as described in the Methods section. Shifted Maxwellian distributions are observed at typical positions (R, Z) as shown in Fig. 3d. Notable heating is observed as the ions flow out into the exhaust from the X-region, as demonstrated in Fig. 3d.
The cause of this anomalously rapid slowdown of ions, together with ion heating, is considered to be the remagnetization of the exiting ions. As the R component of reconnected magnetic field becomes stronger in the downstream region, the ion trajectories (black thick line in Fig. 3c) are significantly affected by the magnetic field of the exhaust and thus ions are remagnetized.
A 2D fully kinetic simulation has been carried out to verify these remagnetization mechanisms and understand how ions are heated downstream (Fig. 3c). In these simulations, realistic MRX global boundary conditions are used in the particle-in-cell (PIC) code VPIC (vectorized particle-in-cell). VPIC is a first-principle, fully kinetic, electromagnetic PIC code that is optimized for large-scale simulations27,28. The system size is about 15 × 30di with 1,200 × 2,400 cells and 350 particles per cell. The mass ratio in the simulations is mi/me=400, ωpe/ωce=1, and the initial electron thermal velocity is 0.125c with Ti=Te. Key physical parameters for the ions such as the ion skin depth and the mean free path are matched to experimentally measured parameters. In the simulations, Coulomb collisions28 are included to study effects of collisions on the ion dynamics.
We obtain good agreement between the observed ion temperature profile and numerical simulation results only with realistic collision frequencies. This shows that ions are almost fully thermalized in the exhaust with a higher temperature than the upstream value. As illustrated with the dashed line in Fig. 3c, the Coulomb collisions enhance the downstream ion thermalization process by scattering ions. In the completely collisionless simulation, on the other hand, the ion distribution is different from Maxwellian. Ion velocity profiles at three different locations—upstream, at the separatrix and downstream—from our PIC simulations with collisions (Fig. 3e) are in reasonably good agreement with experimentally measured profiles (Fig. 3d).
Energy inventory in the two-fluid reconnection layer
When a reconnection electric field is uniformly applied over a wide region in which opposite magnetic field lines meet, such as shown in Fig. 1, electrons with high mobility respond to this field by creating a highly stressed region of magnetic and electric fields caused by Hall effects. This reconnection process partitions inflowing field lines from the reconnected ones by separatrices, across which a notable potential drop (strong electric field) occurs, accumulating large free energy. While electrons are heated at the centre of the reconnection layer, ions are accelerated across the separatrices by the strong electric field and heated through remagnetization by the magnetic field. This electric field structure extends to a very broad region, much wider than the ion skin depth. Now, two important questions are raised: (1) How much energy is transported to particles; and (2) How is that energy partitioned?
Using an energy transport equation analogous to that adopted by Birn and Hesse29, we evaluate how much of the magnetic energy is converted to the kinetic energy of electrons and ions by assessing the energy inventory of the reconnection layer.

where Ls is the loss term for each species including thermal conduction, radiation and ion energy loss to neutrals. The energy inventory is calculated by monitoring the flow of magnetic energy, plasma enthalpy and bulk flow energy simultaneously, while measuring the incoming and outgoing electromagnetic Poynting flux (S), enthalpy flux and bulk flow flux (kinetic energy flux) at a fixed boundary. The boundary of the volume of the plasma, Γb, is given by 31.5≤R≤43.5 cm and 0≤Z≤15 cm (Fig. 1), in which all key local plasma parameters are measured within 10–15% error bars, assuming symmetry with respect to the major axis of the MRX plasma. Figure 4 presents a measured energy inventory, which flows from the magnetic field to plasma particles.
All quantities are shown as rate of energy flow with respect to (WM,in=1.9 MW). The outgoing Poynting flux is sizable in MRX, where two-fluid reconnection occurs because of outgoing energy associated with the Hall-field components. Our quantitative measurements show that half of the incoming magnetic energy is converted to particle energy at a remarkably fast speed, ~0.2(B2/2μ0)VA in comparison with the rate calculated by MHD, (B2/2μ0)VA/S(1/2)=0.03(B2/2μ0)VA; S=900. This difference would become significantly larger for space astrophysical plasmas with much larger S.
It is important to include the components of the Hall magnetic fields in both the incoming and exhaust regions to accurately track the Poynting fluxes. As was done in the study by Birn and Hesse29, isotropic pressure is assumed in this calculation, which is justified in our plasma where anisotropy was only observed in a small region near the X-point. The magnetic energy outflow rate is divided into two components, the conventional MHD part and the Hall-field part associated with the out-of-plane magnetic field and the electrostatic in-plane field. Since the vacuum component of the magnetic field is slowly decreasing during the quasi-steady reconnection period, the first term of the LHS of equation (2) is not negligible. The energy conversion rate to electrons and ions is independently calculated by integrating js·E over the volume Γb. As seen in the Fig. 4, about half of the incoming magnetic energy is converted to particle energy, of which 1/3 goes to electrons (15% of magnetic energy) and 2/3 to ions (25–30% of magnetic energy). In our 2.5D simulation study using the VPIC code, a similar result is obtained. The energy deposited on the electrons becomes thermal energy and is transferred to the exhaust by heat conduction, the energy deposited on the ions is converted to thermal and flow energy with substantial conduction and convection losses. The conversion of magnetic energy in the experiment occurs across a broad region, much larger than considered before.
Discussion
Our quantitative measurements of the acceleration and heating of both electrons and ions demonstrate that more than half of the incoming magnetic energy is converted to particle energy at a remarkably fast speed (~0.2VA) in the reconnection layer. This speed is significantly larger than the value calculated by MHD, 0.03VA for S=900. This difference would become notably larger for space astrophysical plasmas with much larger S. A question arises as to whether the present results should be applied to magnetic reconnection phenomena in space, astrophysical, or fusion plasmas. Recently, in a reconnection region of effectively similar size in the Earth’s magnetotail, the energy partition was carefully measured during multiple passages of the Cluster satellites12. Although the moving X-line in these measurements made it difficult to identify the exact location of the magnetotail-reconnection region, the half length of the tail reconnection layer (L) was estimated to be 2,000–4,000 km namely 3–6di. The normalized scale length of this measurement is very similar to our cases, L~3di. Reconnection in the magnetotail is driven by external force, that is, the solar wind, and the boundary conditions are very similar to the MRX setup. The observed energy partition12 is notably consistent with the present MRX data, namely, >50% of the magnetic energy flux is converted to the particle energy flux, which is dominated by the ion enthalpy flux, with smaller contributions from both the electron enthalpy and heat flux. Also this comparison has implications for its scaling with Lundquist number. When we compare our results from plasmas of S<1,000 with that of the magnetosphere where the Lundquist number is very large (>108), we find that the energy flow pattern is very similar, that is, the energization characteristics do not strongly depend on the Lundquist number. This is consistent with the characteristics of the two-fluid plasma physics, where the classical resistivity based on electron–ion collisions does not play a major role.
Finally, in reversed field pinch fusion plasmas where magnetic reconnection plays a key role in self-organized plasma formation and sustainment, it has been recently reported that a similar portion of magnetic energy (25–30%) is converted to ion thermal energy10. Is there a fundamental physics principle to explain these observations from driven reconnection layers despite some differences in the boundary conditions? We believe the present results represent a key step towards resolving one of the most important problems of plasma physics, how magnetic energy is transferred to plasma particles in the reconnection layer.
Methods
Additional details on diagnostics
Triple Langmuir probes11 are used to measure the electron temperature and density. The density measurements are calibrated by data from a CO2 interferometer. A radial profile of the floating potential is obtained from a 17-tip floating potential probe with maximum resolution of 7 mm. Local ion temperature is measured by IDSPs (ref. 10), which obtain the spectrum of the He II 4686 Å line, which is subsequently fitted to a sum of 13 Gaussian functions to take fine structure effects into account30; without considering fine structure, the ion temperature is overestimated by 15–25%. The time and spatial resolution of the IDSPs are 5.6 μs and 3–4 cm, respectively. Mach probes are used to measure the ion flow velocity due to its better spatial and temporal resolutions. The data from the Mach probe are calibrated by spectroscopic measurements from the IDSPs.
Data acquisition and error analysis
To select the final data set, more than 4,200 discharges were scrutinized based on the reproducibility of the data from the 2D magnetic probe array and a reference Langmuir probe. The main criteria are the location of the X-point, the total plasma current and the density and temperature measured by a reference Langmuir probe. The data values at each measurement point are determined by averaging over 7–15 discharges. The error bars for each measurement are chosen between the standard deviation of each data set and the uncertainty in measurements, whichever is larger. Typical errors in magnetic field measurements are <10%, while those in electrostatic measurements are 15%. The uncertainty in the ion temperature measurements mostly comes from the fitting process and is typically ~15%.
Calculation of the energy inventory
The energy inventory is calculated by integrating each term in equation (2) over the volume Γb. The magnetic energy inflow rate is estimated by

where Sin=(EYBZ/μ0)eR is the incoming Poynting flux. Here eR is the unit vector along the R direction. The outgoing magnetic energy is obtained by integrating the divergence of the outgoing Poynting flux. The outgoing Poynting flux is divided into the MHD component, SMHD=−(EYBR/μ0)eZ and the Hall-field component, SHall=(ERBY/μ0)eZ−(EZBY/μ0)eR. The integration of the first term of the right-hand side of equation (2) indicates the decrease of the magnetic energy per unit time inside vB. Total energy converted to each species per unit time is separately computed by

To obtain change in a specific form of energy, we grouped associated terms in equation (2). The flow energy change of species  is given by
is given by

The thermal energy change of species s is defined as

We note that quantities in the inflow region are taken into account. We estimate the energy loss rate of each species by considering the electron and ion heat flux, electron energy loss by impurity radiation and ion energy loss to neutrals by charge-exchange collisions.
Additional information
How to cite this article: Yamada, M. et al. Conversion of magnetic energy in the magnetic reconnection layer of a laboratory plasma. Nat. Commun. 5:4774 doi: 10.1038/ncomms5774 (2014).
References
Parker, E. N. Sweet's mechanism for merging magnetic fields in conducting fluids. J. Geophys. Res. 62, 509–520 (1957).
Priest, E. & Forbes, T. Magnetic reconnection—MHD theory and applications Cambridge University Press (2000).
Yamada, M., Kulsrud, R. & Ji, H. Magnetic reconnection. Rev. Mod. Phys. 82, 603–664 (2010).
Zweibel, E. G. & Yamada, M. Magnetic reconnection in astrophysical and laboratory plasmas. Annu. Rev. Astron. Astrophys. 47, 291–332 (2009).
Krucker, S. et al. Measurements of the coronal acceleration region of a solar flare. Astrophys. J. 714, 1108–1119 (2010).
Birn, J. et al. Geospace environmental modeling (GEM) magnetic reconnection challenge. J. Geophys. Res. 106, 3715–3719 (2001).
Sonnerup, B. U. Ö. Magnetic Field Reconnection eds Lanzerotti L. T., Kennel C. F., Parker E. N. Vol. 3North-Holland Publishing Co.45–108 (1979).
Wygant, J. R. et al. Cluster observations of an intense normal component of the electric field at a thin reconnecting current sheet in the tail and its role in the shock-like acceleration of the ion fluid into the separatrix region. J. Geophys. Res. 110, A09206 (2005).
Drake, J. F. et al. Ion heating resulting from pickup in magnetic reconnection exhausts. J. Geophys. Res. 114, A05111 (2009).
Fiksel, G. et al. Mass-dependent ion heating during magnetic reconnection in a laboratory plasma. Phys. Rev. Lett. 103, 145002 (2009).
Yoo, J. et al. Observation of ion acceleration and heating during collisionless reconnection in a laboratory plasma. Phys. Rev. Lett. 110, 215007 (2013).
Eastwood, J. P. et al. Energy partition in magnetic reconnection in Earth’s magnetotail. Phys. Rev. Lett. 110, 225001 (2013).
Yamada, M. Progress in understanding magnetic reconnection in laboratory and space astrophysical plasmas. Phys. Plasmas 14, 058102 (2007).
Egedal, J. et al. Evidence and theory for trapped electrons in guide field magnetotail reconnection. J. Geophys. Res. 113, A12207 (2008).
Angelopoulos, V. et al. Electromagnetic energy conversion at reconnection fronts. Science 341, 1478 (2013).
Yamada, M. et al. Study of driven magnetic reconnection in a laboratory plasma. Phys. Plasmas 4, 1936–1944 (1997).
Fiksel, G., Hartog, D. J. D. & Fontana, P. W. An optical probe for local measurements of fast plasma ion dynamics. Rev. Sci. Instrum. 69, 2024–2026 (1998).
Ren, Y. et al. Experimental verification of the Hall effect during magnetic reconnection in a laboratory plasma. Phys. Rev. Lett. 95, 055003 (2005).
Yamada, M. et al. Experimental study of two-fluid effects on magnetic reconnection in a laboratory plasma with variable collisionality. Phys. Plasmas 13, 052119 (2006).
Pritchett, P. L. Onset of magnetic reconnection in the presence of a normal magnetic field: realistic ion to electron mass ratio. J. Geophys. Res. 115, A10208 (2010).
Ji, H. et al. New insights into dissipation in the electron layer during magnetic reconnection. Geophys. Res. Lett. 35, L13106 (2008).
Phan, T. D. et al. Electron bulk heating in magnetic reconnection at Earth’s magnetopause: dependence on the inflow Alfvén speed and magnetic shear. Geophys. Res. Lett. 40, 4475–4480 (2013).
Yoo, J. et al. Bulk ion acceleration and particle heating during magnetic reconnection in a laboratory plasma. Phys. Plasmas 21, 055706 (2014).
Ji, H. et al. Electromagnetic fluctuations during fast reconnection in a laboratory plasma. Phys. Rev. Lett. 92, 115001 (2004).
Ren, Y., Yamada, M., Ji, H., Gerhardt, S. P. & Kulsrud, R. Identification of the electron-diffusion region during magnetic reconnection in a laboratory plasma. Phys. Rev. Lett. 101, 085003 (2008).
Karimabadi, H., Daughton, W. & Scudder, J. Multi-scale structure of the electron diffusion regions. Geophys. Res. Lett. 34, L13104 (2007).
Bowers, K. J. et al. Ultrahigh performance three-dimensional electromagnetic relativistic kinetic plasma simulation. Phys. Plasmas 15, 055703 (2008).
Roytershteyn, V. et al. Driven magnetic reconnection near the Dreicer limit. Phys. Plasmas 17, 055706 (2010).
Birn, J. & Hesse, M. Energy release and conversion by reconnection in the magnetotail. Ann. Geophys. 23, 3365–3373 (2005).
Wiese, W. L. & Fuhr, J. R. Accurate atomic transition probabilities for hydrogen, helium, and lithium. J. Phys. Chem. Ref. Data 38, 565–719 (2009).
Acknowledgements
We appreciate many inputs from W. Daughton for our VPIC simulation and useful discussions with J. Eastwood on space observations. This work is supported by the Department of Energy as well as the NSF-funded Center for Magnetic Self-Organization.
Author information
Authors and Affiliations
Contributions
M.Y. carried out this research by collecting, analyzing and interpreting the data from MRX, and coordinated the experimental results with results from space observation, numerical simulations and theory. J.Y. carried out experimental campaigns and key measurements reported here. He analyzed the data and generated the key figures used in this manuscript. J.J.-A. assisted the experiments and carried out numerical simulations using the VPIC code. H.J., R.M.K., C.E.M. participated in this research by analyzing and interpreting the data from MRX.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Yamada, M., Yoo, J., Jara-Almonte, J. et al. Conversion of magnetic energy in the magnetic reconnection layer of a laboratory plasma. Nat Commun 5, 4774 (2014). https://doi.org/10.1038/ncomms5774
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms5774
This article is cited by
-
Electron scale magnetic reconnections in laser produced plasmas
Reviews of Modern Plasma Physics (2023)
-
Laboratory Study of Collisionless Magnetic Reconnection
Space Science Reviews (2023)
-
Dimensionality of solar magnetic reconnection
Reviews of Modern Plasma Physics (2022)
-
Explosive Magnetotail Activity
Space Science Reviews (2019)
-
Effective Resistivity in Collisionless Magnetic Reconnection
Scientific Reports (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.