Abstract
Over the last decades, views on fisheries management have oscillated between alarm and trust in management progress. The predominant policy for remedying the world fishing crisis aims at maximum sustainable yield (MSY) by adjusting gear selectivity and fishing effort. Here we report a case study on how striving for higher yields from the Eastern Baltic cod stock by increasing selectivity has become exceedingly detrimental for its productivity. Although there is a successive increase in numbers of undersized fish, growth potential is severely reduced, and fishing mortality in fishable size has increased. Once density-dependent growth is introduced, the process is self-enforcing as long as the recruitment remains stable. Our findings suggest that policies focusing on maximum yield while targeting greater sizes are risky and should instead prioritize catch rates over yield. Disregarding the underlying population structure may jeopardize stock productivity, with dire consequences for the fishing industry and ecosystem structure and function.
Similar content being viewed by others
Introduction
After a long period of detrimental levels of fishing mortality worldwide1, management efforts have contributed to some encouraging signs of fish stock recovery, viz. improved abundance and productivity2. One such example is that of the Baltic cod fishery (Fig. 1); after more than two decades of high fishing pressure3, the Eastern Baltic cod stock is by commonly used metrics considered recovered4,5. Exploitation rates have dropped to unexpectedly low levels, and as a result the fishery has since 2011 been Marine Stewardship Council-certified (www.msc.org). Preceding the recovery, fishing gear selectivity was improved by gradually increasing mesh size over the past 15 years, thereby also lowering juvenile mortality6; in fact, higher selectivity in the trawl fishery, which dominates the cod fishing industry, has been one of the prime management objectives since the early 1990s (ref. 7). There are even ongoing discussions on the benefits of targeting even larger size fish, that is fishing at sizes corresponding to global maximum sustainable yield (MSY)8,9; these models have, however, been proved to be based on erroneous assumptions10.
The borders and numbers of the ICES subdivisions are as defined by the International Council for the Exploration of the Sea (www.ices.dk). In recent years, fishing for Eastern Baltic cod takes place almost exclusively in subdivision 25 and 26.
Contesting the alleged recovery of the cod stock is the observation that at present the most probable catch in the Baltic consists of malnourished cod at ~38–40 cm (refs 11, 12). The cod fishing industry is faced with dire economic consequences based on the following figures from a fish processing factory unit: between 2006 and 2011, mean landing size declined by 30%, processing time needed increased on a similar scale and filleting yield declined from 36% to 30% (Fig. 2). The poor growth in Eastern Baltic cod has been explained by density dependence resulting from the high average recruitment in recent years11. This could be due to either increased interspecific or intraspecific food competition12,13,14, potentially exacerbated by oxygen deficit in bottom water layers15.
Mean weight of cod landed in the smallest size category (1–2 kg; bars) and yield, that is, fillet obtained from fresh fish combined for all size categories, not including rejected fish (changes in percentage; dashed line), have decreased, whereas processing time per ton of cod has increased (changes in percentages; black line).
In this study we assessed growth by applying the von Bertalanffy growth model16 to fishery-independent data on length at age to depict and analyse changes in population growth. In this growth model, the length (or weight) asymptote of a fish stock, L∞, reflects the growth potential of the stock and can be expressed as the predicted mean maximum individual size of a population or cohort. L∞ varies with feeding conditions, while the catabolic growth coefficient, K, reflects temperature dependence. Incidence of density-dependent growth in combination with management actions intended to increase selectivity towards bigger size classes was early on predicted to be a potentially malicious combination, which may give considerably lower yields than anticipated16. Raising length at first catch (Lc), measured as the 50% point of the selectivity ogive (that is, the curve of a cumulative distribution function), results in increases in intraspecific competition in size groups left unexploited as population density becomes higher, and, consequently, in decreases in L∞, that is, in the growth potential of the stock. Lower growth potential at sustained levels of recruitment also leads to crowding, as the number of fish will inevitably increase in non-fishable size groups as growth drops. Consequently, fewer fish will reach fishable sizes—further increases in selectivity might even result in an Lc above L∞, which means few fish will reach fishable size.
Density dependence growth is a prime factor regulating population dynamics17,18,19; its occurrence after recruitment in exploited fish stocks is a common phenomenon that needs to be considered20. Increased population densities may lead to higher natural mortality and lower growth, manifesting as lower L∞, seen, for example, in North Sea plaice (Pleuronectes platessa) and haddock (Melanogrammus aeglefinus) stocks after they had augmented during the period of reduced fishing effort during World War II (ref. 16). By contrast, MSY represents a static view on population dynamics; although stock-recruitment relationships are regularly taken into account, density dependence is virtually ignored, while a lower L∞ inevitably leads to lower MSY. Thus, far from being a conservative approach, MSY-oriented management strategies are focused on ensuring that no potential yield is left unexploited.
As a large proportion of all commercial fish stocks have become fully utilized or even depleted over the last decades1, density-dependent growth has so far been absent from most management considerations. However, with exploitation rates being adjusted downwards in many parts of the world2, and stock recoveries becoming increasingly commonplace, density-dependent growth is likely to be a much more widespread phenomenon, especially in cases where increased selectivity constitutes a vital part of envisaged exploitation patterns7,21. A more critical investigation of the ecological implications of the MSY concept is therefore needed, including a search for ‘improved’ selectivity in policy making.
In this study, we found that increased selectivity in the Eastern Baltic cod fishery leads to higher abundance in non-fishable size groups, leading in turn to lower individual growth. With new recruits entering the population, the lower growth induces crowding in smaller, non-fishable size groups, further decreasing growth potential. Meanwhile, as fishing mortality increases in larger fish groups, the rate of culling by cannibalism between size groups can be expected to be reduced, further aggravating the situation. We reproduce these findings by a model using real estimates on recruitment, L∞, mortality rates and selectivity. We argue that the link between higher selectivity and induction of individual density-dependent growth may have implications on MSY-based approaches, in particular when increased selection on larger size classes is an important part of the management strategy.
Here we show that the strive for the theoretically highest yields22 by increasing selectivity is a risk-prone strategy16; as density-dependent growth is induced, stock productivity and population structure may go astray. In search for more robust fisheries management strategies, we argue that catch rates should be prioritized over yield, as it will stabilize yield levels and reduce the need of fishing effort, which will be beneficial for higher ecosystem functionality13.
Results
Effects of selectivity on growth and population number
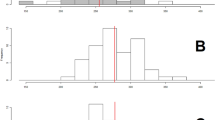
By exploring existing survey data (see ‘Methods’) we show that L∞ has radically decreased for cod year classes recruited since 1995, that is, during the period of increased selectivity (Fig. 3). We also found that the catch-per-unit-effort (CPUE) below minimum landing size (MLS), <37 cm, has strongly increased since the year 2000 (Fig. 4). However, after a period of substantially reduced fishing effort during 2007–2008, with a corresponding notable increase in CPUE above MLS, the CPUE in all fishable sizes dropped conspicuously. This downturn in CPUE was even more dramatic for sizes >45 cm in length; in other words, almost no fish above the present L∞ have been caught in recent years.
The prevailing 50% point of the trawl selectivity ogive, Lc, over time is indicated by a black bar (back-shifted 2 years so as to correspond to year classes at age 2 years). Mean asymptotic length, L∞i, for year class, i, mirroring growth potential (black rhomboids), has dropped conspicuously since 1995 (shown by a 3-year moving average). Correlation between Lc and L∞i, Spearman’s ρ=−0.66 (P<0.001).
Changed mortality patterns
In addition, comparisons between regularly assessed values of total mortality, Z, by the regional scientific advisor at the International Council for the Exploration of the Sea (ICES) (www.ices.dk) and survey-based estimations of Z for fish >37 cm (that is, MLS) showed a deviating pattern over recent years (Fig. 5). Survey-based estimations of Z indicate that mortality for larger fish has remained high, while Z for the length interval 30–37 cm indicates a decline in mortality since the early 2000s; the latter is in agreement with the regular assessment, which includes all fish irrespective of length.
The total mortality, Z (±s.e., estimated by bootstrapping30), has decreased in recent years for smaller cod (30–37 cm and ages 2–4; black line with open circles) whereas Z has increased for larger cod (>37 cm and ages 4–6; black line with triangles). Estimated Z, for all sizes and ages 4–6 according to the regular assessment11 has been added (grey line with squares) for comparison reasons.
Accounting for density-dependent effects
The decline in L∞ is correlated to the total number of fish aged ⩾2 years in the stock, according to the regular assessment11, indicating density dependence (Fig. 6). However, by taking into account changes in selectivity since 1995, modelled natural and fishing mortality rates, and the observed value of L∞ per year class (see ‘Methods’), we could reconstruct the observed developments in numbers ≤37 and >37 cm, respectively, over time (Fig. 7a). By taking into account the observed density dependence of L∞, it could be shown that by keeping selectivity low (Lc=30 cm), crowding of fish ≤37 cm can be avoided (Fig. 7b). In a simulation, using low and moderately high L∞ on yield-per-recruit at three levels of fishing mortality for Eastern Baltic cod clearly indicates that variation in selectivity, Lc, or fishing mortality, F, is much less important than variation in growth potential L∞ (Fig. 8).
Nsj, is equivalent to the number of fish at age ⩾2 years in million, according to the regular assessment11. Nsj is shifted 2 years forward in the regression for year classes 1995–2008 (L∞i=204.5*e−4.022e−9*Nsj; multiple r2=0.54; P<0.001), as to relate the effect of Nsj on L∞i at age 2 years for year-class i.
(a) Predicted numbers of fish at sizes 30–37 (black line and grey circles) and >37 cm (grey line and black triangles) over time from modelled values of Fj, Mj and L∞i, and from recruitment values from routine assessment11 and imposed changes in selectivity. (b) Number of fish 30–37 (black line and grey circles) and >37 cm (grey line and black triangles) over time, modelled by setting Lc at 30 cm, Fj at 0.8 and Mj at 0.3, and estimating L∞i by using the observed density-dependent relationship in Eastern Baltic cod.
Theoretically estimated yield per recruit, Yw/R, from the Eastern Baltic cod stock at a low (L∞ at 45 cm) and high (L∞ at 90 cm) productive state as a function of selectivity, Lc, at three levels of fishing mortality (F at 0.2, 0.5 and 1.5). (L∞ at 45/90 cm are shown with grey/black lines, and F at 0.2/0.5/1.5 are shown with crosses/triangles/open squares, respectively).
Discussion
The lack of cod available to fish in the Eastern Baltic is tightly linked to its lost growth potential, resulting in a steep drop in numbers of fish of fishable size and, furthermore, poor individual status. In fact, L∞ is at present below or close to Lc, which means that few fish are expected to grow above the 50% point of the selectivity ogive, which is equivalent to a fish length of 45 cm. Based on our analysis, the most parsimonious explanation for this process is that increased selectivity has induced a steady increase in number of small-sized fish, which in turn has led to density-dependent growth. The causal mechanism for this process could be related to lower mortality rates for intermediate size groups, partly due to lower catchability as selectivity is increased, and partly due to less predation from larger size groups as they suffer a decline in the relative and absolute abundance over the study period. The process is, then, self-reinforcing: as growth goes down, the number of fish per length group inevitably goes up as long as the recruitment remains at least constant23, which seems to be the case11.
Fishing mortality also appears to be increasing in the size interval still open for exploitation. This implies that a higher fishing effort will not solve the problem. Rather, a combination of both lowered effort and selectivity is required so as to break the present deadlock of density dependence. Lower effort, as being proportionate to F, will also ensure that larger size classes will be re-established, leading to increased natural mortality (M) for smaller size groups due to cannibalism12. As we did not model cannibalism effects on mortality, we may have overestimated the fishing effort needed to cull smaller size groups.
First, our findings contradict the MSY framework in place11. All indicators outside the single-stock assessment results of Fmsy imply severe economic losses for the fishing industry. In addition, there are apparent risks of fishery-induced evolution in size and age at maturity24, not to mention ecosystem losses of eroding important predatory fish from the Baltic Sea ecosystem13. Tentatively, given this example, we may conclude that managing with MSY diverts attention from the fact that total allowable catches (TACs) increasingly overshoot biomass availability in Eastern Baltic cod11. Meanwhile, the regional advising agency is suggesting a 7% TAC increase for 2014 (ref. 25). As a recent higher estimate of Fmsy allows for even larger increases in TACs, it was noted that even higher exploitation rates will deal with ‘the excessive Eastern cod stock density problem’25 and that no regulations of effort will be needed in the future.
Second, our results disagree with current policies of increased selectivity21. There is still a widespread, and unfortunate, preference for improvements in yield over improvements in CPUE26, thereby, ignoring economic constraints as well as the benefits of a more pristine size distribution with higher food web stability27. Furthermore, if the lower individual growth potential has indeed been reduced because of factors other than dynamic interplay caused by increased selectivity, lower selectivity is still an appropriate response to the present situation in the Eastern Baltic cod fishery: a reduced number of fish will inevitably increase food resources for the survivors, and thereby restore some of the former growth pattern.
The Johannesburg declaration22 of an ‘MSY target’ for all marine fish stocks was made without reference to the selectivity or effort involved: that is, the costs of fishing, either economic or ecological in nature, were not considered. Instead of a search for a maximum output by fine-tuning selectivity and effort (a solution which will become obsolete as soon as the growth potential of the stock changes), a decrease in effort and selectivity will be a superior risk-averting strategy16,27,28. In fact, it would be much more profitable for individual fishermen to fish slightly less than fishing at MSY (Fmsy), because it would lead to higher CPUE10,16, and would arguably be more environmentally benign because less effort is involved26. Prioritizing robust harvest strategies, where CPUE is a crucial estimate on stock status, is arguably more economical and ecologically safe in the longer perspective compared with options related to yield. Although it was introduced with good intentions, a selectivity shortcut to improve yield, profit and ecosystem structure does not exist. Rather, as is illustrated with this case of the Eastern Baltic cod, the policy of increasing selectivity has altered the ecosystem structure of the Baltic Sea, for which the effect may be augmented in the future if proper actions are not taken.
Methods
Maps
Maps showing the Baltic Sea region and Europe were produced by using the software Ocean Data View (http://odv.awi.de). Information on the delineation of ICES subdivisions in the Baltic Sea was gathered at www.ices.dk.
Information on commercial landings
Data on commercial landings of both western and eastern Baltic cod between 2004 and 2011 were gathered from a fish processing unit in Poland. This data includes information on mean weight, trimming time and fillet yield for fresh fish, collected on a regular basis for all cod processed.
Modelling of growth potential
Survey age-specific catch rates from ICES survey data for subdivisions 25–29 (Fig. 1) (DATRAS at www.ices.dk) were used for parameterizing von Bertalanffy’s growth model, as follows29:

where Li is the expected or average length at time (or age) t, L∞i is the asymptotic average length of year class i, K is the Brody growth rate coefficient (units are per year) and t0 is a modelling artefact that represents the time or age when the average length was zero. Modelling of data to the von Bertalanffy growth equation was performed using fisheries stock assessment software (FSA fishR; http://www.rforge.net/FSA/). The number of iterations for convergence was set to 50 and different initial values of L∞i and K were tested so as to let the model converge. L∞i, which mirrors the feeding conditions of a cohort16, was estimated as year class mean for two separate surveys in the first and fourth quarter of the year.
Modelling of mortality rates
Total mortality, Zj, was determined from survey data using SURBA software30. Natural mortality rates, Mj, were estimated from life history parameters31 (http://cran.r-project.org/web/packages/fishmethods/).
Modelling of density dependence
The relationship between the year class-specific length asymptote, L∞i, and stock numbers, in year, j, Nsj, was modelled with an exponential function by using modelled values of L∞i for year classes 1995–2008 and corresponding summed stock numbers, Nsj, in year, j, in million, according to published assessment estimates11 (see Fig. 6) when year class, i, was at age 2 years:

Modelling of population dynamics
Population numbers of fish ≤37 and >37 cm were modelled by using observed L∞i per year class i and by setting growth factor K and reference age t0 to 0.3 and −0.2, respectively. The mean length, Lij, of year class i at year j was estimated using equation (1).
To simulate a normal size distribution at year, j, each year class, i, was divided into seven cohorts, v. Each cohort, v, followed its own growth and population trajectory in the model. Each cohort represents a fixed proportion of the year class, i: 38%, 2 × 15%, 2 × 9.2%, 2 × 6.8%. The corresponding mean length of cohort by year class and year was estimated as Lijv, Lijv±0.5 s.e. of the mean size, Lijv±1 SE, Lijv±1.5 SE. As the mean coefficient of variation of the observed lengths for ages 2–10 years during the time period 1991–2013 was observed at c. 0.2, the mean sizes Lijv of the seven cohorts per year and year class were accordingly estimated as Lijv, Lijv±0.1 × Lij, Lijv±0.2 × Lij, Lijv±0.3 × Li. Number, N, for year class and cohort at year, j, Nivj was determined by the following equation:

where Niv(j−1) is the number of survivors in the preceding year (j−1) and t is the age interval (set to 1 year). For each year class, i, the starting year of estimation is the year of recruitment at age 2 years, where Niv2 is the recruitment for year class and cohort at age 2 years, using published assessment recruitment values11. Where the mean length of cohort for year class and year was below the 50% point of the selectivity ogive, that is, Lijv<Lc, fishing mortality, Fj, was set to 0.
Modelling of yield
To model yields at various levels of exploitation rate E (E=F/Z) and selectivity Lc, lifetime percentage yield, y, was calculated for L∞i at 45 and 90 cm by the following yield function32:

where Ωn=+1, −3, +3, −1 for n=0, 1, 2 and 3, respectively; c= Lc/L∞i. Further, m=M/K is a mortality–growth ratio. In this study, M and K were set at 0.3 (that is, m=1). For calculation of yield per recruit Yw/R, the following equation was used as a way to return to original scaling:

where Yw is the yield in weight, tr is the age at recruitment to a fishable size and W∞i is the mean asymptote weight. W∞i was calculated using the weight–length relationship:

where published values for Eastern Baltic cod a=0.104 and b=3 were used9.
Additional information
How to cite this article: Svedäng, H. & Hornborg, S. Selective fishing induces density-dependent growth. Nat. Commun. 5:4152 doi: 10.1038/ncomms5152 (2014).
References
Pauly, D. et al. Towards sustainability in world fisheries. Nature 418, 689–695 (2002).
Worm, B. et al. Rebuilding global fisheries. Science 325, 578–585 (2009).
Zeller, D. et al. The Baltic Sea: Estimates of total fisheries removals 1950–2007. Fish. Res. 108, 356–363 (2011).
Cardinale, M. & Svedäng, H. The beauty of simplicity in science: Baltic cod stock improves rapidly in a ‘cod hostile’ ecosystem state. Mar. Ecol. Prog. Ser. 425, 297–301 (2011).
Eero, M., Köster, F. W. & Vinther, M. Why is the Eastern Baltic cod recovering? Mar. Policy 36, 235–240 (2012).
Feekings, J., Lewy, P. & Madsen, N. The effect of regulation changes and influential factors on Atlantic cod discards in the Baltic Sea demersal trawl fishery. Can. J. Fish. Aquat. Sci. 70, 534–542 (2013).
Madsen, N. Selectivity of fishing gears used in the Baltic Sea cod fishery. Rev. Fish. Biol. Fisheries 17, 517–544 (2007).
Froese, R., Stern Pirlot, A., Winker, H. & Gascuel, D. Size matters: how single-species management can contribute to ecosystem-based fisheries management. Fish. Res. 92, 231–241 (2008).
Cardinale, M. & Hjelm, J. Size matters: Short term loss and long term gain in a size-selective fishery. Mar. Policy 36, 903–906 (2012).
Svedäng, H. Comments to Froese et al. (2008): Size matters: Ne quid nimis. Fish. Res. 149, 74–75 (2014).
ICES Report of the ICES advisory committee. ICES Advice. Books 1–11, International Council for the Exploration of the Sea (2013) (www.ices.dk).
Eero, M. et al. Spatial management of marine resources can enhance the recovery of predators and avoid local depletion of forage fish. Conserv. Lett. 5, 486–492 (2012).
Casini, M. et al. Trophic cascades promote threshold-like shifts in pelagic marine ecosystems. Proc. Natl Acad. Sci. USA 106, 197–202 (2009).
Lindegren, M., Möllmann, C., Nielsen, A. & Stenseth, N. C. Preventing the collapse of the Baltic cod stock through an ecosystem-based management approach. Proc. Natl Acad. Sci. USA 106, 14722–14727 (2009).
Teschner, E. C. et al. Impact of hypoxia on consumption of Baltic cod in a multispecies stock assessment context. J. Appl. Ichthyol. 26, 836–842 (2010).
Beverton, R. J. H. & Holt, H. J. On the Dynamics of Exploited Fish Populations (Fishery Investigations, Series II, 19Her Majesty’s Stationery Office: London, (1957).
Verhulst, P. F. Notice sur la loi que la population poursuit dans son accroissement. (Note on the law how the population regulates its growth) [in French.]. Corr. Math. Phys. 10, 113–121 (1838).
Andrewartha, H. G. & Birch, L. C. The Distribution and Abundance of Animals University of Chicago Press (1954).
Turchin, P. Rarity of density dependence or population regulations with lags? Nature 344, 660–663 (1990).
Lorenzen, K. & Enberg, K. Density-dependent growth as a key mechanism in the regulation of fish populations: evidence from among-population comparisons. Proc. R. Soc. Lond. B 269, 49–54 (2002).
Regulation (EU) No 1380/2013 of the European Parliament and of the Council of 11 December 2013 on the Common Fisheries Policy, amending Council Regulations (EC) No 1954/2003 and (EC) No 1224/2009, and repealing Council Regulations (EC) No 2371/2002 and (EC) No 639/2004, and Council Decision 2004/585/EC. Official Journal of the European Union 28.12.2013 (2013).
United Nations. Report of the World Summit on Sustainable Development, Johannesburg, South Africa, 26 August to 4 September 2002. Tech. Report No. A/CONF.199/20, New York (2002).
Andersen, K. H. & Beyer, J. E. Asymptotic size determines species abundance in the marine size spectrum. Am. Nat. 168, 54–61 (2006).
Olsen, E. M. et al. Maturation trends indicative of rapid evolution preceded the collapse of northern cod. Nature 428, 932–935 (2004).
BALTFISH. Common proposal for 2014 Baltic Seas TACs and quotas. BALTFISH High Level Group under the Latvian Presidency http://www.fishsec.org/2014/05/07/final-discussions-on-a-discard-ban-plan-for-the-baltic-sea-discussed-in-baltfish/ (2013).
Longhurst, A. Mismanagement of Marine Fisheries Cambridge University Press (2010).
Garcia, S. M. et al. Reconsidering the consequences of selective fisheries. Science 335, 1045–1047 (2012).
Law, R. Fisheries-induced evolution: present status and future directions. Mar. Ecol. Prog. Ser. 335, 271–277 (2007).
Quinn, T. J. II & Deriso, R. B. Quantitative Fish Dynamics Oxford University Press (1999).
Needle, C. Fleet Dynamics in Fisheries Management Strategy Evaluations. Ph.D. thesis, University of Strathclyde. http://ethos.bl.uk/OrderDetails.do?uin=uk.bl.ethos.576261 (2012).
Pauly, D. On the interrelationships between natural mortality, growth parameters, and mean environmental temperature in 175 fish stocks. J. Cons. Int. Explor. Mer. 39, 175–192 (1980).
Beverton, R. J. H. & Holt, S. J. Tables of Yield Functions for Fishery Assessment. Fisheries Division, Biology Branch, Food and Agriculture Organization of the United Nations (1964).
Acknowledgements
This study was funded by a grant from Baltic Sea 2020 (www.Balticsea2020.org) and by the Swedish Research Council Formas. We thank Professor David Righton at CEFAS, UK, for comments on an earlier draft. We are also indebted to Mr Alex Olsen at A. Espersen A/S, Denmark, for kindly providing us with data from the processing industry.
Author information
Authors and Affiliations
Contributions
H.S. contributed the original idea for this work, and was involved with planning, modelling and writing this paper. S.H. contributed to planning and writing.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/4.0/
About this article
Cite this article
Svedäng, H., Hornborg, S. Selective fishing induces density-dependent growth. Nat Commun 5, 4152 (2014). https://doi.org/10.1038/ncomms5152
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms5152
This article is cited by
-
Deoxygenation impacts on Baltic Sea cod: Dramatic declines in ecosystem services of an iconic keystone predator
Ambio (2022)
-
Environmental performance of blue foods
Nature (2021)
-
Intraspecific competition of predator for prey with variable rates in protected areas
Nonlinear Dynamics (2020)
-
Baltic Sea ecosystem-based management under climate change: Synthesis and future challenges
AMBIO (2015)
-
Baltic Sea management: Successes and failures
AMBIO (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.