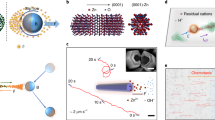
Abstract
Co-operativity is a remarkable phenomenon mostly seen in biology, where initial reaction events significantly alter the propensity of subsequent reaction events, giving rise to a nonlinear tightly regulated synergistic response. Here we have found unique evidence of atomic level co-operativity in an inorganic material. A thousand-atom nanocrystal (NC) of the inorganic solid cadmium selenide exhibits strong positive co-operativity in its reaction with copper ions. A NC doped with a few copper impurities becomes highly prone to be doped even further, driving an abrupt transition of the entire NC to the copper selenide phase, as manifested by a strongly sigmoidal response in optical spectroscopy and electron diffraction measurements. The examples presented here suggest that cooperative phenomena may have an important role in the solid state, especially in the nucleation of new chemical phases, crystal growth, and other materials’ transformations.
Similar content being viewed by others
Introduction
Since the first observation in 1910 of the co-operative binding of oxygen to haemoglobin1,2, where binding at any of the four sites of haemoglobin increases the oxygen affinity of the other sites, co-operative phenomena have been displayed in a host of macromolecular systems3, ranging from the unwinding of DNA and protein folding4 to self-assembly in supramolecular systems5. A common feature of co-operative systems is that they possess multiple binding sites with some mechanism for feedback or coupling between the binding sites. The feedback itself may be positive or negative. Positive co-operativity is manifested as an apparent all-or-nothing behaviour6: rather than making a gradual progression through intermediary states, the system undergoes a relatively abrupt transition from the initial to the final state in response to an extremely small change in conditions (for example, ligand, denaturing agent, pH or temperature). The system spends little time in the intermediary states, resulting in their low population. The strongly sigmoidal oxygen-binding curve of haemoglobin is the archetypal example of such behaviour1.
Although examples of co-operativity seem limited to macromolecules, mostly biological3, we found evidence of co-operative behaviour in an inorganic solid material. The observation was made in nanocrystals (NCs) of cadmium selenide (CdSe)7 undergoing a cation exchange in the presence of monovalent ions as:

In this transformation8,9, the Cd2+ cationic sub-lattice is replaced with Cu+ ions, two for every Cd2+ ion, to form a NC of cuprous selenide (Cu2Se). Each CdSe NC is ∼4 nm or ∼1,300 atoms in size, and loosely speaking, can be thought of as a ‘macromolecular system’ with multiple ‘sites’ for foreign cations. The cation exchange reaction10 itself has received a lot of fundamental attention because of its remarkably fast (millisecond timescale) kinetics11 in nanosized crystals. The transformation, if well understood, can be exploited for topotaxially templated synthesis of nanostructures with novel compositions and morphologies12,13, designing heterojunctions in NCs14, sensing heavy metal ions15, and achieving electronic doping16,17.
With limited mechanistic insight available, cation exchange is often assumed to be a diffusion-limited transformation: as long as the cation can diffuse to a lattice site, exchange can take place at that site. By this assumption, all lattice sites exposed to Cu+ would have an equal affinity for exchange and the CdSe ensemble would transform in a random site-by-site manner to the Cu2Se phase as adequate Cu+ becomes available. However, our optical and electron diffraction measurements show that the exchange transformation does not follow such a memoryless, diffusion-limited process. Instead, we see positive co-operative behaviour, where initial Cu+ doping of a NC strongly enhances the likelihood of further Cu+ doping within the same NC, causing the NC to transition sharply from a lightly doped CdSe NC to the Cu2Se phase.
Results
Optical probing of cation exchange
We used excitonic absorption spectra (Fig. 1a) to monitor the cation exchange of a solution of 4-nm CdSe NCs as it was titrated with Cu+. With increasing Cu+ feed concentration, the excitonic band at 2.1 eV, corresponding to the 1 Sh–1 Se transition in the CdSe NCs, decreased in intensity, which is expected as the conversion to Cu2Se proceeded. Concomitantly, the absorption in the near-infrared region associated with Cu2Se increased.
Excitonic absorption spectra (a) of an ensemble of CdSe NCs as a function of added Cu+. Feed Cu+ concentrations are denoted as the number of ions available per CdSe NC. With increasing addition of Cu+, the CdSe NC exciton peak at 2.1 eV decreases without undergoing any shift. Concomitantly, the Cu2Se absorption in the near-infrared increases. A clear isosbestic point is seen. Following complete exchange, the absorption spectrum of the NCs resembles that of Cu2Se with a bandgap onset around 1 eV. Note, Cu2Se is an indirect semiconductor and therefore has no excitonic band, rather only a featureless absorption above its bandgap. PL spectra (b) in the sub-bandgap region show the emergence of defect luminescence when Cu+ is added, which evolves further with increasing Cu+ feed concentration. The excitonic bandgap PL of CdSe NCs was subtracted out from these spectra, as detailed in the Methods section.
Two important features emerge in these spectra. First, the spectral position of the CdSe exciton stayed relatively unchanged throughout the titration, which indicates an absence13 of any significant fraction of binary CdSe/Cu2Se NCs formed by partial cation exchange. Such heterostructures would exhibit strongly shifted excitonic peaks, because the excitonic peak position is highly dependent on the CdSe crystallite size18. Although it is possible that partial conversion of a CdSe NC to Cu2Se completely quenches its excitonic absorption, this possibility is excluded by a key observation: the decrease in the fraction of CdSe NCs (estimated from the CdSe exciton height) is perfectly correlated with the increase in the fraction of Cu2Se NCs (estimated from the Cu2Se absorbance at 1.82 eV), as shown in Fig. 2. A clear isosbestic point (Fig. 1a) is identified, which is a well-known indicator of a two species system, where one species converts to another over the course of the titration. Thus, it appears that individual CdSe NCs switch fully to Cu2Se as sufficient Cu+ becomes available. With increasing amount of Cu+, more and more NCs make this transition from CdSe to Cu2Se. Thus, each NC is either in the CdSe state (albeit with some Cu+ dopants) or in the fully exchanged Cu2Se state, manifesting the classic two-state behaviour of a co-operative system.
Experimental plot (a) of the fraction of NCs in the CdSe state (black) and those in the Cu2Se state (blue) as a function of added Cu+ is strikingly sigmoidal, representative of a strongly co-operative process. Below a critical concentration of ∼500 Cu+ ions per NC, very few NCs undergo a transition to the Cu2Se state. A fit to the Hill plot (solid black line, R=0.996) yields a co-operativity factor of nH=7.1. Note we use total Cu+ concentration, although the Hill equation is strictly valid for free concentrations. The fraction of NCs in the CdSe state was determined from the height of the CdSe excitonic peak from Fig. 1a and the fraction in the Cu2Se state was determined from the Cu2Se band-to-band absorption at 1.82 eV. The procedure for analysis is described in Methods. The rise in the Cu2Se fraction tracks well with the drop in the CdSe fraction, further confirming two-state behaviour. The defect luminescence intensity (red), integrated across the broad band shown in Fig. 1b increased as Cu+ was added, until it reached a maximum around the critical concentration, beyond which it decreased, until it reached zero. A theoretical simulation (b) of a 20-site NC reproduced the observed nature of the cation exchange transformation. Sequential binding was used to model the positive co-operative behaviour. The simulated fraction of Cu2Se NCs in solution as a function of the total Cu+ concentration, plotted as the number of ions per NC, follows a strongly sigmoidal curve (blue). The fraction of all NCs in the CdSe state, either pure or doped, is also shown (black). The simulated concentration of Cu+ dopants and associated Cd2+ vacancies (red) reproduces the observed evolution of the defect luminescence. The defect concentration reaches a maximum around the critical Cu+ concentration, beyond which it gradually decreases to zero.
Across a range of systems, sigmoidal-binding curves are a definitive manifestation of co-operative behaviour1. Figure 2 shows such a curve for the cation exchange process: this plot of the fraction of NCs in the CdSe state as a function of Cu+ concentration is strikingly sigmoidal, as also is the plot of the fraction of NCs in the Cu2Se state. Only a small to negligible fraction of NCs is exchanged at low Cu+ feed concentrations. However, once a critical concentration is reached, a major fraction of NCs switch to the Cu2Se state over a narrow concentration window about the critical concentration. The titration curve fits well (R=0.996) the Hill equation1, with a Hill coefficient or co-operativity factor of nH=7.1. As a comparison, strongly co-operative oxygen binding by haemoglobin shows a value of nH=2.3–3.0. We have found some experiment-to-experiment variation in the measured nH (range 4–7). Size/shape/surface-related heterogeneities inherent to NC samples may contribute to such variation.
Structural probing of cation exchange
Electron diffraction measurements (Fig. 3) provide structural evidence of the sharp onset of the cation exchange process. The initial NC samples show wurtzite CdSe diffraction features, which persist up to a Cu+ feed concentration as high as 549 ions per NC (Table 1). Around this Cu+ concentration (the half-way point), a significant fraction of NCs undergo a conversion to Cu2Se, as indicated by the emergence of diffraction features corresponding to the tetragonal belladoite phase of Cu2Se, albeit superimposed on wurtzite diffraction features from the remnant CdSe NCs. With further addition of Cu+, the tetragonal Cu2Se diffraction pattern becomes more prominent as additional NCs convert to Cu2Se. Concomitantly, the wurtzite CdSe diffraction pattern wanes. Eventually, at about 1,317 Cu+ ions per NC (slightly higher than a full stoichiometric amount), only the tetragonal Cu2Se diffraction pattern is seen, indicating conversion of all NCs to Cu2Se.
For NCs subject to 0 Cu+ ions per NC and 384 Cu+ ions per NC respectively (a,b), selected area electron diffraction patterns are indicative of the CdSe wurtzite (cadmoselite) structure. As shown in Table 1, the innermost ring at 3.55 Å is a combination of the (100), (002) and (101) planes, which are Debye–Scherrer broadened into one ring. The three outer rings, measured at 2.15, 2.00 and 1.88 Å, match those for the (100), (103) and (200) planes of cadmosellite. In addition, there is a ring corresponding to the (102) plane, at a lattice spacing of 2.55 Å. These features are seen for samples (a–c). At 1,317 Cu+ ions per NC (in slight excess of the stoichiometric amount needed for full conversion), the tetragonal Cu2Se phase (bellidoite) is seen (e). The highest intensity reflections include ones at 3.46 Å for the (113), (311) and (222) planes, 2.04 Å for the (404) plane, and 1.76 Å for the (226) and (533) plane. The diffraction features of Cu2Se seem to first appear at 549 Cu+ ions per NC (c), overlapped with CdSe diffraction features. As exchange progresses, CdSe diffraction features wane, until a pure bellidoite diffraction pattern is obtained for the fully converted sample. All d-spacings are determined relative to the (111) reflection of an Au standard taken under the same conditions. Samples were prepared by a slow titration of CdSe NCs in toluene with increasing amounts of a methanolic solution of Cu+, similar to the titration experiments described in Methods. At various points in the titration, a small aliquot was drop-casted onto an ultrathin carbon transmission electron microscope grid and washed with methanol several times. The total amount of Cu+ added is indicated in Table 1 in the form of number of ions per NC, estimated as described in Methods.
Cu+ doping as a precursor to exchange
In the regime below the critical concentration, it is clear that there is little conversion to Cu2Se and most of the NCs exhibit the CdSe crystal structure. However, in this regime, the NCs are doped with Cu(1+) impurities, as found from X-ray photoelectron spectroscopy (XPS) (Fig. 4b,c and Supplementary Fig. S1) and elemental analyses (Supplementary Fig. S2 and Supplementary Table S1). Cu+ is a common interstitial dopant in CdSe19,20. It is known that such dopants do not necessarily disrupt the excitonic band or the overall crystallographic structure of CdSe18,19, which is consistent with our optical and electron diffraction measurements.
A model of a CdSe wurtzite crystal (a) with ordered cadmium (red) and selenium (yellow) atoms. Below the critical concentration, the CdSe NC uptakes copper ions (blue) in the form of interstitial dopants, in turn creating Cd2+ vacancies within the NC for charge compensation. These impurities and vacancies are manifested in the emergence of defect luminescence in Fig. 1b. Initial doping events can greatly enhance the affinity of the NC for additional Cu+, eventually triggering a sharp transition to the Cu2Se state. The formation of a Cu2Se NC involves the mutual annihilation of Cu+ dopants and Cd2+ vacancies, resulting in the decrease in defect luminescence seen above the critical concentration. High-resolution XPS of NCs treated with a copper concentration of 325 Cu+ ions per NC are shown (b). NCs were thoroughly washed with methanol to remove excess Cu+ before measurements. The fitted peak position of the Cu 2p3/2 band (932.5 eV) is indicative of copper ions in the 1+ oxidation state. The Cu LMM peak in the X-ray induced Auger spectrum (c), used to differentiate between Cu+ and Cu0, shows a fitted peak position of 917.2 eV, characteristic of Cu(1+). Additional XPS data are shown in the Supplementary Information.
Cu+ doping can, however, cause lattice defects: for instance, for every two interstitial Cu+ impurities in a NC, charge compensation would require the formation of a Cd2+ vacancy. Both Cu+ impurities and vacancies serve as mid-gap trap states and give rise to sub-bandgap luminescence21,22,23,24, which we employed for monitoring the doping of NCs at various stages in the cation exchange titration (Fig. 1b). Whereas pure CdSe NCs show no sub-bandgap luminescence, addition of Cu+ induces a broad defect luminescence in the sub-bandgap 1.4–1.8 eV region. With increasing Cu+ feed concentration, the defect luminescence increased in intensity, as would be consistent with an increase in copper impurities and associated defects prior to the onset of cation exchange. The defect luminescence intensity reached a maximum around the critical Cu+ concentration, beyond which it started decreasing. Such a decrease is expected from the sharp onset of cation exchange, because the transition to Cu2Se involves mutual annihilation of Cu+ impurities with Cd2+ vacancies, expressed in Kroger–Vink notation as:

Thus, doping of a CdSe NC with Cu+ appears to be a critical precursor to the onset of cation exchange (Fig. 4a). The strongest affirmation comes from two observations in Fig. 2a: first, the point in the titration where the defect luminescence intensity reaches a maximum is coincident with the point of onset of cation exchange. Second, the plot of defect luminescence intensity as a function of feed Cu+ concentration resembles the derivative of the sigmoidal titration curve.
Discussion
The extended latent region below the critical concentration suggests that the initial incorporation of Cu+ into the lattice is a relatively low-probability process. However, initial doping of a NC can occur stochastically, possibly at surface or defect sites of a NC. These initial doping events activate the NC for further doping. Each doping event enhances the affinity of the NC for a subsequent doping event and so on, until the NC reaches a critical state where it is likely to take up every available Cu+ ion, resulting in a cascade of Cu+ incorporation and an abrupt phase transition from a low-doped CdSe NC to Cu2Se. In other words, a NC already doped with Cu+ is much more likely to take up additional Cu+ and make a sharp transition to Cu2Se, albeit at the expense of another NC which has acquired none or relatively few dopants. This bias represents positive co-operativity between ‘sites’ on the same NC.
When energetic aspects of such positive co-operative behaviour were included in a lattice site model (Methods section)25, we were able to simulate all our experimental observations (Fig. 2b). We started with an ensemble of CdSe NCs, each with 20 bivalent sites for Cu+. For the first doping event within any NC, the magnitude of the free energy change ΔG was assumed to be small, making it a low probability event. However, each doping event increased, by an amount Δg, the free energy change resulting from subsequent doping on the same NC. Thus, it is energetically more and more favourable for a NC to incorporate Cu+ ions. This simple model reproduced the strongly sigmoidal response of the NC ensemble to the added Cu+. There was an extended latent region during which only a tiny fraction of NCs made a transition to Cu2Se. Most of the NCs made a transition over a narrow window around a critical Cu+ feed concentration. The simulations also reproduced the rise in the number of defects in the ensemble with increasing Cu+ feed concentration. The number of defects reached a maximum around the critical concentration, following which it gradually decreased to zero. If there were no such positive co-operative bias (that is, if every site in the CdSe ensemble had a similar affinity for Cu+ regardless of whether the site is on an already doped NC or an undoped one), the exchange process would be a diffusion-limited one. In such a case, each NC would exchange gradually via a continuum of intermediary CdSe/Cu2Se heterostructure states. The titration curve would be Langmuirian (nH=1) rather than sigmoidal (nH>1).
Thus, a positive co-operative model, similar to one employed in biomacromolecular systems26, captures the observed behaviour of the cation exchange process. Nevertheless it still leaves open the question of the atomistic mechanism for co-operativity. In haemoglobin, oxygen binding at one of the heme subunits leads to a conformational change in the neighbouring subunits, which increases the affinity of the neighbour site for oxygen binding, a phenomenon known as allostery22. Allosteric coupling between lattice sites of a NC can originate from a few different structural factors. As described earlier, owing to charge compensation, Cu+ doping results in the creation of Cd2+ vacancies, one vacancy for every two interstitial Cu+ impurities. These lattice vacancies provide hopping sites for enhanced in-diffusion of additional Cu+ ions into the NC and out-diffusion of Cd2+ ions from the NC. Second, the local negative polarization at a Cd2+ vacancy site could electrostatically attract other positively charged Cu+ ions. Third, inclusion of interstitial impurities and formation of vacancies would strain the NC lattice greatly enhancing the thermodynamic driving force for Cu+ substitutions and structural transition to Cu2Se. Such mechanisms have been found to be operative in super-ionic solids27.
Cation exchange with another common monovalent cation Ag+ showed similar results: a sigmoidal titration curve and a maximum in the defect luminescence intensity around the critical concentration (Fig. 5), indicating that the co-operative mechanism of cation exchange is not specific just to Cu+. The Ag system appears to be less co-operative than the Cu system: the titration curve is not as steep. The Hill fit shows a value of nH=3.2 smaller than for Cu+. The plot of the defect luminescence intensity as a function of feed concentration does not show a sharp peak, rather a plateau. Although the physical reason for this difference is not understood, it could be due to the significantly larger size of Ag+ than Cu+. The larger Ag+ ions may have a lower propensity to occupy interstitial sites and substitutional doping may be more prevalent than in the Cu+ case.
A plot of the fraction of NCs in the CdSe state (black dots) and those in the Ag2Se state (blue) as a function of added Ag+ is sigmoidal, indicative of co-operative behaviour. Below a critical concentration of ∼500 Ag+/NC, very few NCs undergo a transition to the Ag2Se state. A fit to the Hill plot (solid black line, R=0.973) yields a co-operativity factor of nH=3.2. The fraction of NCs in the CdSe state was determined from the height of the CdSe excitonic peak and the fraction in the Ag2Se state was determined from the Ag2Se band-to-band absorption at 1.82 eV. The absorption and PL data is shown in Supplementary Fig. S5, and the procedure for analysis is described in Methods. The rise in the Ag2Se fraction tracks well with the drop in the CdSe fraction. The defect luminescence intensity (red), integrated across its broad band, increases as Ag+ is added, until it reaches a maximum around the critical concentration, beyond which it decreases, until it reaches zero.
Although positive co-operativity between sites of individual NCs explains all our observed results, a related mechanism is worth considering. It is possible for initial Cu (or Ag) impurities formed within a NC to cluster together into a critical-size nucleus, initiating spontaneous growth of the Cu2Se (or Ag2Se) phase within the NC. This is reminiscent of the photographic development of silver iodide, where a latent four-atom nucleation cluster triggers rapid spontaneous growth of Ag28,29,30. Such a nucleation–growth mechanism could give rise to the observed two-state behaviour and the sharp sigmoidal transition. However, the topotactic nature of cation exchange31 is not compatible with a nucleation-driven mechanism. In the latter mechanism, the final nanostructure morphology would be dictated by the growing nucleus, rather than by the starting ionic template.
A common feature across many co-operative systems is that each binding event pre-organizes other sites for binding, thereby reducing the number of non-productive configurations and resulting in greatly enhanced reaction rates. For instance, co-operativity allows a protein to fold rapidly within milliseconds, rather than requiring the protein to sample all possible configurations. The latter would need a time longer than the age of the universe. It is possible that cation exchange reactions in NCs are driven to completion due to the strongly co-operative nature of the transition.
Akin to co-operativity between molecular units in the biological world, co-operativity between atoms may be ubiquitous in the solid state, where there is no dearth of multi-site systems. Formation of defects, interfaces or strain may provide the required inter-site interactions. Co-operative behaviour in solid-state systems needs closer attention, especially in relation with closely linked processes such as phase transitions and nucleation32,33 and due to the utility of co-operative phenomena in predicting and controlling materials’ transformation outcomes. Nonlinear behaviour induced by co-operativity may allow the design of sensors with tight regulation.
Methods
Synthesis of CdSe NCs
The procedure for synthesis of CdSe NCs was adapted from Manna and co-workers34. Three grams of trioctylphosphine oxide, 0.280 g of octadecylphosphonic acid (ODPA) and 0.060 g of cadmium oxide were mixed in a 25 ml three neck flask, heated to 150 °C and exposed to vacuum for 1 h. Under argon, the solution was heated to 320 °C and held at that temperature until the solution was optically clear, indicating complete dissolution of cadmium oxide. At this point, 1.5 g of tri-n-octylphosphine (TOP) was injected into the flask. The flask was heated to 370 °C and a TOP-Se solution (0.058 g of selenium powder and 0.360 g of TOP) was injected into the flask. The reaction time was 1 min for obtaining CdSe NCs of 4 nm diameter. After the synthesis, the NCs were repeatedly precipitated with methanol followed by re-dissolution in toluene.
Stoichiometry calculations for cation exchange titrations
For titrations, the initial concentration of Cd2+ ions from the CdSe NCs in each reaction cuvette was determined. From the position of the first exciton, λ, the diameter, D, of the NC and the extinction coefficient were calculated using the equations35:


The NCs used in all the titrations had a diameter of ∼4 nm. The extinction coefficient  and the absorbance at the first exciton were used to determine the concentration of NCs. From the diameter, the volume and mass of NCs was calculated, from which the total mass and molar amount of Cd2+ ions in each CdSe NC solution was determined. All titrations were done with approximately equal concentrations of CdSe NCs. Each Cu+ titration involved 4.8 × 10−6 mol of Cd2+ ions being exchanged with one stoichiometric equivalent of Cu+ ions (9.6 × 10−6 mol of Cu(I)PF6) dissolved in 200 μl of methanol. The details for each incremental addition in the titration is given in Supplementary Table S2. The right-most column of this table was used as the x axis value for the titration plots shown in Fig. 2.
and the absorbance at the first exciton were used to determine the concentration of NCs. From the diameter, the volume and mass of NCs was calculated, from which the total mass and molar amount of Cd2+ ions in each CdSe NC solution was determined. All titrations were done with approximately equal concentrations of CdSe NCs. Each Cu+ titration involved 4.8 × 10−6 mol of Cd2+ ions being exchanged with one stoichiometric equivalent of Cu+ ions (9.6 × 10−6 mol of Cu(I)PF6) dissolved in 200 μl of methanol. The details for each incremental addition in the titration is given in Supplementary Table S2. The right-most column of this table was used as the x axis value for the titration plots shown in Fig. 2.
Cation exchange procedure
All exchange reactions were carried out in septa-capped 3.5 ml quartz cuvettes. In an oxygen and moisture-free glove box, CdSe NCs were dispersed in 3.0 ml of toluene. Initial Cd2+ molar amounts were calculated as described above to be 4.8 × 10−6 mol Cd2+. In total, 9.6 × 10−6 mol of tetrakis(acetonitrile)copper(I) hexafluorophosphate (Cu(I)PF6) in 200 μl of methanol was added during each titration. NC samples were prepared in the glove box in air-free conditions and kept in air-free cuvettes during the exchange reactions. Additions took place outside of the glove box. A solution of Cu(I)PF6 in methanol, prepared in the glove box and kept sealed during the experiment, was sequentially added to the reaction cuvette with a microliter syringe, taking care that the solution or sample were not exposed to air. Samples were stirred vigorously after each addition and the solution was allowed to equilibrate while stirring for ∼1 h, which is a time much in excess of the typical reaction time for complete cation exchange (<1 s). Absorption and photoluminescence (PL) spectra were then taken.
Optical spectroscopy measurements
Absorption spectra of exchanged CdSe NCs were collected on a Shimadzu UV-3600 scanning spectrophotometer with a 1 nm step size with toluene as a reference solvent. PL spectra of NCs were taken in toluene on a Cary Eclipse fluorimeter. Spectra were taken in the 650–900 nm wavelength range, where defect luminescence appears. All PL measurements were performed using the same slit width (5 nm), scan speed (120 nm/min), excitation wavelength (450 nm) and photomultiplier tube voltage.
Analysis of absorption and PL spectra
The total volume change over the entire titration was <10%, therefore correction of spectra for volumetric dilution was not necessary. The acquired absorbance spectra contain absorption from both unexchanged CdSe NCs and formed Cu2Se NCs. The absorption contribution of the formed Cu2Se NCs was subtracted from the acquired spectra to isolate the absorption of unexchanged CdSe NCs as follows:

Here, we use the fact that at 1.82 eV, the absorption contribution from CdSe is negligible. The absorbance A at the first exciton peak of the corrected spectrum is proportional to the concentration of unexchanged CdSe NCs in solution as per Beer–Lambert’s law. This absorbance A normalized to a value of 100% at 0% exchange is equal to the percentage of CdSe NCs that is still unexchanged. This percentage was plotted as a function of Cu+ added in Fig. 2a. The absorbance of Cu2Se at 1.82 eV (that is, above its bandgap absorption onset) can be used to estimate the relative concentration of Cu2Se NCs produced over the course of the titration. The absorbance at 1.82 eV normalized to a value of 100% at full exchange is equal to the percentage of Cu2Se NCs formed. This percentage was also plotted in Fig. 2a as a function of Cu+ feed concentration.
PL spectra were corrected by removing the contribution from the excitonic PL of CdSe NCs as follows:

After this correction, the defect luminescence bands were integrated between 650 and 900 nm. The integrated defect PL signal was plotted in Fig. 2a as a function of Cu+ feed concentration. We also performed a control experiment to confirm that methanol exposure alone does not give rise to defect PL in the NCs (Supplementary Fig. S3).
Electron microscopy
High-resolution transmission electron microscopy (HRTEM) images were taken using a JEOL 2010 LaB6 operating at 200 kV. High-angle annular dark-field scanning electron transmission microscopy (HAADF-STEM) images were acquired on a JEOL 2010F at 200 kV with a 0.5 nm size beam. Samples of NCs were prepared by drop-casting NCs in toluene on an ultrathin carbon grid followed by repeated washing with methanol.
NC morphology
HRTEM and HAADF-STEM images (Supplementary Figs S4 and S5) show the morphology of NCs as a function of the feed Cu+ concentration in Cu+ ions per NC. Samples were made from adding Cu(I)PF6 in 200 μl methanol to CdSe NCs in toluene. The NCs were drop-casted from this toluene:methanol mixture onto a Cu grid, followed by washing with methanol to remove excess Cu+ and Cd2+ resulting from exchange. Images show preservation of size and morphology throughout the exchange process. NC sizing analysis was performed on HAADF-STEM images. Lattice fringes in HRTEM show that NCs maintain crystallinity throughout the exchange process.
Elemental analysis
ICP-OES (inductively coupled plasma optical emission spectrometry) was performed on a Perkin-Elmer Optima 2000 DV instrument. To prepare samples, NCs were repeatedly washed and precipitated with methanol to remove excess ions in solution. Approximately 1 mg of each sample was digested with 16 M HNO3 and subject to ICP-OES analysis for determination of the molar ratios of Cd, Cu and Se (Supplementary Table S1).
Exchange with Ag+
Titration experiments with Ag+ were performed in an identical manner as those with Cu+. Initial Cd2+ molar amounts were calculated as described above to be 4.4 × 10−6 mol of Cd2+ in each cuvette. In total, 8.9 × 10−6 mol of silver nitrate (AgNO3), corresponding to one stoichiometric equivalent, was the calculated amount to be added over the entire titration Slightly more was actually found to be needed (1.1 × 10−5 mol of AgNO3 in 240 μl of methanol) to ensure complete disappearance of the first exciton peak of CdSe.
Absorption and PL spectra were corrected and processed using the same methods described earlier. Uncorrected absorption spectra (Supplementary Fig. S6a) were baseline corrected (Supplementary Fig. S6c) to account for absorption of Ag2Se NCs. The CdSe exciton peak heights were then analysed to estimate the percentage of NCs exchanged as a function of Ag+ added (Fig. 5). The PL spectra (Supplementary Fig. S6b) were corrected (Supplementary Fig. S6d) to remove the band-edge PL. Following correction, the defect luminescence band was integrated to obtain the trend in defect luminescence intensity as a function of Ag+ added (Fig. 5).
X-ray photoelectron spectroscopy
XPS analysis was performed on NCs exchanged with 0, 325 and 651 Cu+ ions per NC. A Kratos Axis ULTRA instrument was used, which uses a monochromatized Al Kα X-ray source of 15 kV (∼10 mA). The instrument consisted of separate specimen transfer and analysis chambers, typically operated at 5E−07 and 1E−09 Torr, respectively. The Cu 2p3/2 spectrum was fitted with 30% Gaussian/70% Lorentzian peak shapes. C 1s peak was used as a reference. The samples subject to 325 and 651 Cu+ ions per NC (Fig. 4b and Supplementary Fig. S1c respectively) show a Cu 2p3/2 with a fitted peak position of 932.5 eV, which suggests a 1+ oxidation state. To distinguish between Cu0 and Cu+, high-resolution spectra were collected around the X-ray-induced Cu LMM Auger peak (shown in Fig. 4c and Supplementary Fig. S1d). The peak position of 917.2 eV (K.E.) corresponds to Cu(1+). The absence of the Cu(1+) peak in the Cu 2p3/2 (Supplementary Fig. S1a) and Cu LMM (Supplementary Fig. S1b) spectra for the unexchanged sample confirms that there is no Cu in the original CdSe NCs.
Theoretical model
We simulated the response of NCs using a lattice-site model. Each NC was assumed to have a size of n=20 sites, each of which can incorporate two Cu+ ions. Co-operativity was introduced in this model by requiring that doping takes place sequentially: only when a doping event has taken place at the first site in the NC does a second site become available in that NC, and so on.

here M, ML, ML2 and so on are relative concentrations of NC complexes from CdSe through to Cu2Se and k1, k2, k3 and so on are association constants for each sequential doping step.

We assumed that the association constant of the first doping event k1 has a relatively small magnitude (10−2 M−1). However, the first step enhances the free energy for the second step by an amount Δg, and the second step enhances that of the third one and so on. Therefore,

or,

where a=exp−Δg/kT. As Δg is negative, a is a positive integer, which we term as the interaction parameter. The magnitude of a depends directly on the magnitude of free energy stabilization (Δg) relative to thermal energy (kT). For instance, a 0.1-eV stabilization can result in a ∼55, which was a typical value used in the simulations. A higher value of a would allow the transition to be achieved over a narrower concentration window for the same value of k1.
For a free Cu+ concentration c and Cd2+ concentration d, concentrations of the different NC complexes can be given in terms of the concentration of unexchanged CdSe NCs M as:

In general,

where we define a dimensionless k:

The fraction of NCs in the pure CdSe state is given by:

where

The fraction of NCs in the Cu2Se state is given by:

1-MLn/MT gives the fraction of NCs that are either purely CdSe or Cu-doped CdSe. The total concentration of Cu+ dopants is given by:

Note in the above expression Cu+ ions in Cu2Se state are not included as they are no longer in the form of dopants and do not contribute to defect luminescence. Free Cu+ ions in solution are not included either. cd is also equal to two times the concentration of Cd2+ vacancies. The concentration of Cu+ incorporated in the NCs, including in the form of Cu2Se, is given by:

The free Cd2+ concentration is given by:

The free Cu+ concentration is given by:

and the total Cu+ concentration as:

Additional information
How to cite this article: White, S.L. et al. Co-operativity in a nanocrystalline solid-state transition. Nat. Commun. 4:2933 doi: 10.1038/ncomms3933 (2013).
References
Hill, A. V. The possible effects of the aggregation of the molecule of hemoglobin on its dissociation curves. J. Physiol. 40, iv–vii (1910).
Akers, G. K., Doyle, M. L., Myers, D. & Daugherty, M. A. Molecular code for cooperativity in hemoglobin. Science 255, 54–63 (1992).
Whitty, A. Cooperativity and biological complexity. Nat. Chem. Bio. 4, 435–439 (2008).
Shank, E. A., Cecconi, C., Dill, J. W., Marqusee, S. & Bustamante, C. The folding cooperativity of a protein is controlled by its chain topology. Nature 465, 637–640 (2010).
Prince, R. B., Saven, J. G., Wolynes, P. G. & Moore, J. S. Cooperative conformational transitions in phenyl ethylene oligomers: chain-length dependence. J. Am. Chem. Soc. 121, 3114–3121 (1999).
Hunter, C. A. & Anderson, H. L. What is Cooperativity? Angew. Chem. Int. Ed. 48, 7488–7499 (2009).
Dukes, A. D., McBride, J. R. & Rosenthal, S. J. Synthesis of the magic-sized CdSe and CdTe nanocrystals with diisooctylphosphinic acid. Chem. Mater. 22, 6402–6408 (2010).
Don, H. S., Hughes, S. M., Yin, Y. & Alivisatos, A. P. Cation exchange reactions in Ionic Nanocrystals. Science 306, 1009–1012 (2004).
Robinson, R. D. et al. Spontaneous superlattice formation in nanorods through partial cation exchange. Science 317, 355–358 (2007).
Pollok, K., Putnis, C. V. & Putnis, A. Mineral replacement reactions in solid solution-aqueous solution systems: Volume changes, reactions paths and end-points using the example of model salt systems. Am. J. Sci. 311, 211–236 (2011).
Chan, E. M. et al. Millisecond kinetics of nanocrystal cation exchange using microfluidic x-ray absorption spectroscopy. J. Phys. Chem. A. 111, 12210–12215 (2007).
Miszta, K. et al. Hierarchical self-assembly of suspended branched colloidal nanocrystals into superlattice structures. Nat. Mater. 10, 872–876 (2011).
Kovalenko, M. V. Quasi-seeded growth of ligand-tailored PbSe nanocrystals through cation-exchange-mediated nucleation. Angew. Chem. Int. Ed. 47, 3029–3033 (2008).
Jain, P. K., Amirov, L., Aloni, S. & Alivisatos, A. P. Nanoheterostructure cation exchange: anionic framework preservation. J. Am. Chem. Soc. 132, 9997–9999 (2010).
Li, J., Zhang, T., Yin, Y. & Zhong, W. Fluorescence signal amplification by cation exchange in ionic nanocrystals. Angew. Chem. Int. Ed. 48, 1588–1591 (2009).
Sahu, A. et al. Electronic impurity doping in CdSe nanocrystals. Nano Lett. 12, 2587–2594 (2012).
Mocatta, D. et al. Heavily doped semiconductor nanocrystal quantum dots. Science 332, 77–81 (2011).
Norris, D. J., Sacra, A., Murray, C. B. & Bawendi, M. G. Measurement of the size dependent hole spectrum in CdSe quantum dots. Phys. Rev. Lett. 72, 2612–2615 (1994).
Opik, A. I. & Varvas, J. A. Defect structure of Cu-Doped cadmium selenide. Phys. Stat. Sol. 74, 467–473 (1982).
Grandhi, G. K., Tomar, R. & Viswanatha, R. Study of surface and bulk electronic structure of II-VI semiconductor nanocrystals using Cu as a nanosensor. ACS Nano 6, 9751–9763 (2012).
Meulenberg, R. W. Structure and composition of Cu-doped CdSe nanocrystals using soft x-ray absorption spectroscopy. Nano Lett. 4, 2277–2285 (2004).
Sakalas, A. & Baubinas, R. Scattering centers and their relation to the recombination centres in single crystals of CdSe. Phys. Stat. Sol. 31, 301–307 (1975).
Türe, I. E., Claybourn, M., Brinkman, A.,W. & Woods, J. Defects in cadmium selenide. J. Cryst. Growth 72, 189–193 (1985).
Kokubun, Y., Watanabe, H. & Wada, M. Photoluminescence of CdSe single crystals. Jpn J. Appl. Phys. 13, 1393–1398 (1974).
Monod, J., Wyman, J. & Changeaux, J. P. On the nature of allosteric transitions: a plausible model. J. Mol. Biol. 12, 88–118 (1965).
Weiss, J. N. The Hill equation revisited: uses and misuses. FASEB J. 11, 835–841 (1997).
Hainovsky, N. & Maier, J. Premelting, sublattice melting, and overall melting in Frenkel disordered ionic crystals. Solid State Ionics 76, 199–205 (1995).
Fayet, P. et al. The role of small silver clusters in photography. Z. Phys. D 3, 299–302 (1986).
Gurney, R. W. & Mott, N. F. The theory of the photolysis of silver bromide and the photographic latent image. Proc. Roy. Soc. 164, 151–167 (1937).
Mott, N. F. The photographic process. Nature 175, 234–236 (1955).
Rivest, J. B. & Jain, P. K. Cation exchange on the nanoscale: an emerging technique for new material synthesis, device fabrication, and chemical sensing. Chem. Soc. Rev. 42, 89–96 (2013).
Baumgartner, J. et al. Nucleation and growth of magnetite from solution. Nat. Mater. 12, 310–314 (2012).
Gebauer, D., Völkel, A. & Cölfen, H. Stable prenucleation calcium carbonate clusters. Science 322, 1819–1822 (2008).
Carbone, L. et al. Synthesis and micrometer-scale assembly of colloidal CdSe/CdS nanorods prepared by a seeded growth approach. Nano Lett. 7, 2942–2950 (2007).
Yu, W. W., Qu, L., Guo, W. & Peng, X. Experimental determination of the extinction coefficient of CdTe, CdSe, and CdS nanocrystals. Chem. Mater. 15, 2854–2860 (2003).
Acknowledgements
We thank Melika Fini and Alex Stanton for assistance with preliminary experiments. P.K.J. acknowledges support from the DuPont Young Professor Award and Frederick Seitz Materials Research Laboratory, where characterization was performed.
Author information
Authors and Affiliations
Contributions
S.L.W. prepared samples, designed and performed measurements, analysed and interpreted data and co-wrote the manuscript. J.G.S. performed electron microscopy characterization. M.B. performed XPS measurements. P.K.J. conceived project, designed experiments, developed concepts and theory, analysed and interpreted data and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures S1-S6, Supplementary Tables S1-S2 and Supplementary Reference (PDF 1073 kb)
Rights and permissions
About this article
Cite this article
White, S., Smith, J., Behl, M. et al. Co-operativity in a nanocrystalline solid-state transition. Nat Commun 4, 2933 (2013). https://doi.org/10.1038/ncomms3933
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms3933
This article is cited by
-
Telluride semiconductor nanocrystals: progress on their liquid-phase synthesis and applications
Rare Metals (2022)
-
Mechanistic insight into copper cation exchange in cadmium selenide semiconductor nanocrystals using X-ray absorption spectroscopy
Nature Communications (2021)
-
Surface modification-induced phase transformation of hexagonal close-packed gold square sheets
Nature Communications (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.