Abstract
Among the applications of optical phase measurement, the differential interference contrast microscope is widely used for the evaluation of opaque materials or biological tissues. However, the signal-to-noise ratio for a given light intensity is limited by the standard quantum limit, which is critical for measurements where the probe light intensity is limited to avoid damaging the sample. The standard quantum limit can only be beaten by using N quantum correlated particles, with an improvement factor of √N. Here we report the demonstration of an entanglement-enhanced microscope, which is a confocal-type differential interference contrast microscope where an entangled photon pair (N=2) source is used for illumination. An image of a Q shape carved in relief on the glass surface is obtained with better visibility than with a classical light source. The signal-to-noise ratio is 1.35±0.12 times better than that limited by the standard quantum limit.
Similar content being viewed by others
Introduction
Quantum metrology involves using quantum mechanics to realize more precise measurements than those that can be achieved classically1. The canonical example uses entanglement of N particles to measure a phase with a precision Δφ=1/N, known as the Heisenberg limit. Such a measurement outperforms the  precision limit possible with N unentangled particles—the standard quantum limit (SQL). Progress has been made with trapped ions2,3,4 and atoms5, whereas high-precision optical phase measurements have many important applications, including microscopy, gravity wave detection, measurements of material properties, and medical and biological sensing. Recently, the SQL has been beaten with two photons6,7,8,9,10 and four photons11,12,13.
precision limit possible with N unentangled particles—the standard quantum limit (SQL). Progress has been made with trapped ions2,3,4 and atoms5, whereas high-precision optical phase measurements have many important applications, including microscopy, gravity wave detection, measurements of material properties, and medical and biological sensing. Recently, the SQL has been beaten with two photons6,7,8,9,10 and four photons11,12,13.
Perhaps the next natural step is to demonstrate entanglement-enhanced metrology14,15,16. Among the applications of optical phase measurement, microscopy is essential in broad areas of science from physics to biology. The differential interference contrast microscope (DIM)17 is widely used for the evaluation of opaque materials or the label-free sensing of biological tissues18. For instance, the growth of ice crystals has recently been observed with a single molecular step resolution using a laser confocal microscope (LCM) combined with a DIM19. The depth resolution of such measurements is determined by the signal-to-noise ratio (SNR) of the measurement, and the SNR is in principle limited by the SQL. In the advanced measurements using DIM, the intensity of the probe light, focused onto a tiny area of ~ 10−13 m2, is tightly limited for a non-invasive measurement, and the limit of the SNR is becoming a critical issue.
In this work, we demonstrate an entanglement-enhanced microscope, consisting of a confocal-type differential interference contrast microscope equipped with an entangled photon source as a probe light source, with an SNR of 1.35 times better than that of the SQL. We use an entangled two-photon source with a high fidelity of 98%, resulting in a high two-photon interference visibility in the confocal microscope setup of 95.2%. An image of a glass plate sample, where a Q shape is carved in relief on the surface with a ultra-thin step of ~ 17 nm, is obtained with better visibility than with a classical light source. The improvement of the SNR is 1.35±0.12, which is consistent with the theoretical prediction of 1.35. We also confirm that the bias phase dependence of the SNR completely agrees with the theory without any fitting parameter. We believe this experimental demonstration is an important step towards entanglement-enhanced microscopy with ultimate sensitivity.
Results
The limit of differential interference contrast microscope
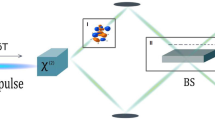
Our entanglement-enhanced microscope is based on a laser confocal microscope combined with a differential interference contrast microscope (LCM–DIM)19,20. An LCM–DIM can detect a very tiny difference between optical path lengths in a sample. The LCM–DIM works on the principle of a polarization interferometer (Fig. 1a). In this example, the horizontal (H) and vertical (V) polarization components are directed to different optical paths by a Nomarski prism. At the sample, the two beams experience different phase shifts (ΔφH and ΔφV) depending on the local refractive index and the structure of the sample. After passing through the sample, the two beams are combined into one beam by another Nomarski prism. The difference in the phase shifts can be detected as a polarization rotation at the output, Δφ=ΔφV−ΔφH.
We obtain differential interference contrast images for a sample by scanning the relative position of the focused beams on the sample (Fig. 1c–e). When two beams probe a homogeneous region, the output intensity is constant (Fig. 1c). At the boundary of the two regions, the signal intensity increases or decreases, as the difference in the phase shift Δφ becomes non-zero (Fig. 1d). The signal intensity returns to the original level after the boundary (Fig. 1e). The smallest detectable change in the phase shift is limited by the SNR, which is the ratio of the change in the signal intensity, C(φ), and the fluctuation of the uniform background level, ΔC, at a bias level of Φ0. As is discussed in detail later, it is known that the SNR is limited by so-called ‘shot noise' or the SQL, when classical light sources such as lasers or lamps are used. That is, for a limited number of input photons (N), the SNR is limited by  . This SNR limits the height resolution of the LCM–DIM when used to observe elementary steps at the surface of ice crystals19 or the difference in refractive indexes inside a sample. Thus, improving the SNR beyond the SQL is a revolutionary advance in microscopy.
. This SNR limits the height resolution of the LCM–DIM when used to observe elementary steps at the surface of ice crystals19 or the difference in refractive indexes inside a sample. Thus, improving the SNR beyond the SQL is a revolutionary advance in microscopy.
Entanglement-enhanced microscope
We propose to use multi-photon quantum interference to beat this standard quantum limit (Fig. 1b). Instead of a classical light, we use an entangled photon state ( ), so-called ‘NOON’ state, which is a quantum superposition of the states ‘N photons in the H polarization mode’ and ‘N photons in the V polarization mode’. The phase difference between these two states is NΔφ after passing through the sample, which is N times larger than the classical case (N=1). At the output, the result of the multi-photon interference (the parity of the photon number in the output) is measured by a pair of photon number discriminating detectors21,22.
), so-called ‘NOON’ state, which is a quantum superposition of the states ‘N photons in the H polarization mode’ and ‘N photons in the V polarization mode’. The phase difference between these two states is NΔφ after passing through the sample, which is N times larger than the classical case (N=1). At the output, the result of the multi-photon interference (the parity of the photon number in the output) is measured by a pair of photon number discriminating detectors21,22.
As is well known from two-path interferometry with N-photon states, entanglement can increase the sensitivity of a phase measurement by a factor of  . In the entanglement-enhanced microscope, we apply this effect to achieve an SNR that is
. In the entanglement-enhanced microscope, we apply this effect to achieve an SNR that is  times higher than that of the LCM–DIM. If the average number of N-photon states that pass through the microscope during a given time interval is k, then the average number of detection events in the output is given by C(φ)=kP(φ), where P(φ)=(1−VN cos(Nφ+NΦ0))/2 is the probability of detecting an odd (or even) number of photons in a specific output polarization (see Methods section). For a small positive phase shift of
times higher than that of the LCM–DIM. If the average number of N-photon states that pass through the microscope during a given time interval is k, then the average number of detection events in the output is given by C(φ)=kP(φ), where P(φ)=(1−VN cos(Nφ+NΦ0))/2 is the probability of detecting an odd (or even) number of photons in a specific output polarization (see Methods section). For a small positive phase shift of  , the phase dependence of the signal is given by the slope of C(φ) at the bias phase Φ0, limΔφ→0|C(Δφ)−C(0)|=|∂C(φ)/∂φ||φ=0 × Δφ, and the SNR is given by the ratio of the slope and the statistical noise of the detection. If the emission of the N-photon states is statistically independent, the statistical noise is given by
, the phase dependence of the signal is given by the slope of C(φ) at the bias phase Φ0, limΔφ→0|C(Δφ)−C(0)|=|∂C(φ)/∂φ||φ=0 × Δφ, and the SNR is given by the ratio of the slope and the statistical noise of the detection. If the emission of the N-photon states is statistically independent, the statistical noise is given by  . The SNR is then given by
. The SNR is then given by

where ξ is the normalized overlap region between the two beams at the sample plane (see Methods section). By maximizing the function of cos(NΦ0), we can find the maximum sensitivity (SNRmax) as follows:

at a bias phase of

For the ideal case of VN=1, the maximum sensitivity  . As the SNR for a classical microscope using kN photons
. As the SNR for a classical microscope using kN photons  , an entanglement-enhanced microscope can improve the SNR by a factor of
, an entanglement-enhanced microscope can improve the SNR by a factor of  compared with a classical microscope for the same photon number.
compared with a classical microscope for the same photon number.
Experimental setup
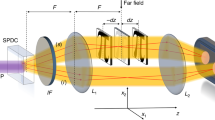
We demonstrate an entanglement-enhanced microscope (Fig. 2a) using a two-photon NOON state (N=2). First, a polarization-entangled state of photons  is generated from two beta barium borate crystals23,24 and is then delivered to the microscope setup via a single-mode fibre. The polarization-entangled state is then converted to a two-photon NOON state
is generated from two beta barium borate crystals23,24 and is then delivered to the microscope setup via a single-mode fibre. The polarization-entangled state is then converted to a two-photon NOON state  using a calcite crystal25 and focused by an objective lens. From the result of quantum state tomography (Fig. 2b), the fidelity of the state is 98% and the entanglement concurrence is 0.979, which ensures that the produced state is almost maximally entangled. The entangled photons pass through two neighbouring spots at the sample plane (Fig. 2a inset). Then, after passing through the collimating lens, the two paths are merged by a polarization beam splitter and the result of the two-photon interference is detected by a pair of single-photon counters and a coincidence counter. The sample is scanned by a motorized stage to obtain an image. The beam diameters at the sample plane and the distance between the centre of the beams are all 45 μm (ξ=0.046).
using a calcite crystal25 and focused by an objective lens. From the result of quantum state tomography (Fig. 2b), the fidelity of the state is 98% and the entanglement concurrence is 0.979, which ensures that the produced state is almost maximally entangled. The entangled photons pass through two neighbouring spots at the sample plane (Fig. 2a inset). Then, after passing through the collimating lens, the two paths are merged by a polarization beam splitter and the result of the two-photon interference is detected by a pair of single-photon counters and a coincidence counter. The sample is scanned by a motorized stage to obtain an image. The beam diameters at the sample plane and the distance between the centre of the beams are all 45 μm (ξ=0.046).
(a) BBO: beta barium borate; PP: phase plate; PBS: polarizing beam splitter. A 405-nm diode laser (line width <0.02 nm) was used for the pump beam. A sharp-cut filter with a cut-off wavelength below 715 nm and a band pass filter with 4 nm bandwidth were used. The beam displacement at the calcite crystal was 4 mm. PBS reflects vertical polarization component and transmits horizontal polarization. The blue and red lines indicate the optical paths for the horizontally and vertically polarized beams. The inset shows an illustration of the sample with the trajectory of the two beams. (b) The absolute value of the reconstructed density matrix of the generated state measured before the microscope setup (after the output coupler) using quantum state tomography45. HV denotes for the state where one photon is horizontally polarized and the other photon is vertically polarized. (c) Single-photon interference fringes of a classical microscope (counts per second) after the dark counts of the detectors (100 cps) subtracted. (d) Two-photon interference fringes of an entanglement-enhanced microscope (5 cps). While varying the phase by rotating the phase plate (PP), we counted the detected events in the output. The classical fringe was measured by inserting a polarizer transmitting the diagonally polarized photons and counting single-photon detection events. Solid lines in c and d are by theoretical fitting curve. Error bars are given by Poissonian statistics.
Figure 2c,d shows the single-photon and two-photon interference fringes using a classical light source and the NOON source, respectively. The fringe period of Fig. 2d is half that of Fig. 2c, which is a typical feature of NOON state interference. The visibilities of these fringes, Vc=97.1±0.4% (Fig. 2c) and Vq=95.2±0.6% (Fig. 2d), suggests the high quality of the classical and quantum interferences.
Obtained image beating the standard quantum limit
Figure 3 shows the main result of this experiment. We used a glass plate sample (BK7) on whose surface a Q shape is carved in relief with an ultra-thin step of ~ 17 nm using optical lithography (Fig. 3a,b). Figure 3c,d shows the two-dimensional (2D) scan images of the sample using entangled photons and single photons, respectively. The step of the Q-shaped relief is clearly seen in Fig. 3c, whereas it is obscure in Fig. 3d. Note that for both images we set the bias phases to almost their optimum values given in equation 3 and the average total number of photons (N × k) contributed to these data are set to 920 per position assuming the unity detection efficiency.
(a) Atomic force microscope (AFM) image of a glass plate sample (BK7) on whose surface a Q shape is carved in relief with an ultra-thin step using optical lithography. (b) The section of the AFM image of the sample, which is the area outlined in red in a. The height of the step is estimated to be 17.3 nm from this data. (c) The image of the sample using an entanglement-enhanced microscope where two-photon entangled state is used to illuminate the sample. (d) The image of the sample using single photons (a classical light source). (e,f) One-dimensional fine scan data for the area outlined in red in c and d for the same photon number of 920. The measurement was made at a bias phase of 0.41 (e) and 0.66 (f), where optimal bias phases are 0.38 and 0.67, respectively. Solid lines are theoretical fitting curves (see text). (g,h) The histogram of the counts at 400 experimental points of the background level for e and f. Red curves are the Poisson distribution with the average of the counts at 400 points (83.3 and 110.9, respectively).
For more detailed analysis, the cross-section of the images (coincidence count rate per single count rate at each position) are shown in Fig. 3e,f. The solid lines are theoretical fits to the data where the height and position of the step and the background level are used as free parameters. For Fig. 3e, the signal (the height of the peak of the fitting curve from the background level) is 20.21±1.13, and the noise (the standard deviation of each experimental counts from the background level of the fitting curve) is 9.48 (Fig. 3g). Thus, the SNR is 2.13±0.12. Similarly, the signal, the noise and the SNR are 17.7±1.22, 11.25 (Fig. 3h) and 1.58±0.11 for Fig. 3f, where classical light source (single photons) is used. The improvement in SNR is thus 1.35±0.12, which is consistent with the theoretical prediction of 1.35 (equation 2). The estimated height of the step was 17.0±0.9 nm (quantum) and 16.6±1.1 nm (classical), and is consistent with the estimated value of 17.3 nm from the atomic force microscope image in Fig. 3b.
As shown in equation 1, the SNR depends on the bias phase. Finally, we test the theoretical prediction of the bias phase dependence given by equation 1 in actual experiments. Figure 4 shows the bias phase dependence of the SNR for the two-photon NOON source (Fig. 4a) and classical light source (Fig. 4b). The solid curve is the theoretical prediction calculated by equation (1), where we used the observed visibilities of the fringes in Fig 2c,d for VN. The theoretical curves are in good agreement with the experimental results.
(a) Dependence of the SNR on the bias phase using an entanglement-enhanced microscope (N=2). (b) Dependence of the SNR on the bias phase using a classical microscope. The SNR and its error shown by error bars were calculated from the experimental data similar to Fig. 3e,f taken for different bias phases. The total photon number Nk=1,150 for a and 1,299 for b. The solid line shows the theoretical curve using equation (1).
Discussion
Note that the entanglement-enhanced microscope we reported here is different from the ‘entangled photon microscope’ theoretically proposed by Teich and Saleh26, which is the combination of two photon fluorescence microscopy and the entangled photon source. In the proposal, the increase in two-photon absorption rate and the flexibility in the selection of target regions in the specimen were predicted. The application of entangled photon sources for imaging also includes quantum lithography27, where the lateral resolution of the generated pattern is improved25,28, and ghost imaging29, where the spatial correlation of entangled photons is utilized. In this context, this work is the first application of entanglement-enhanced optical phase measurement beyond the SQL for imaging including microscopy. Note also that the entanglement is indispensable to improve the SNR of the phase measurement beyond the SQL11,30. This situation is different from the improvement in the contrast of the ghost imaging using strong thermal light31,32,33,34,35,36,37.
In conclusion, we proposed and demonstrated an entanglement-enhanced microscope, which is a confocal-type differential interference contrast microscope equipped with an entangled photon source as a probe light source, with an SNR 1.35±0.12 times better than the SQL. Imaging of a glass plate sample with an ultra-thin step of ~ 17 nm under a low photon number condition shows the viability of the entanglement-enhanced microscope for light-sensitive samples. To test the performance of the entanglement-enhanced microscope, we used modest-efficiency detectors, however, recently developed high-efficiency number-resolving photon detectors would markedly improve detection efficiency38,39. We believe this experimental demonstration is an important step towards entanglement-enhanced microscopy with ultimate sensitivity, using a higher NOON state, a squeezed state40,41 and other hybrid approaches42 or adaptive estimation schemes43,44.
Methods
SNR of an entanglement-enhanced microscope
To perform the parity measurement used by Gerry21 and Seshadreesan et al.22, it is required to count both of the events where ‘even’ and ‘odd’ number of photons are detected in the output. However, experimental implementations become much easier if it is sufficient for us to just count ‘odd’ (or ‘even’) number photon-detection events. In addition, the distance between the two beams and the beam size may have effect on the SNR. Here we consider these technical effects on SNR and derive equation (1).
To derive equation (1), we consider that the two beams at the sample are separated at a distance of α along the x axis, and each set of N photons has Gaussian distribution with a variance of σ in the x–y plane (Fig. 5). After passing through the sample, the two beams experience a phase shift (φ) in the grey region (x>0). The state, |Ψ(x, y, φ), after the sample is written as
The beams are in V polarization (blue) and H polarization (red) on the sample, corresponding to Fig. 1c–e. The grey shaded region has the phase change of φ.

where |ψH(x,y,φ) and |ψV(x,y,φ) represents the states of N photons in the horizontal and vertical polarization modes, respectively, and Φ0 is a bias phase. We assume that the phase shift is described by a step function and the N photons are in the same spatial modes. These states are written as

where |0› is a vacuum state,  and
and  are the creation operators in H and V polarization modes at the position of (x,y), respectively, and χ(x) is a step function that χ(x)=0 for x ≤0 and χ(x)=1 for x>0. f(x−α/2, y) and f(x+α/2, y) represent the N-photon probability densities in the horizontal and vertical polarization modes written as
are the creation operators in H and V polarization modes at the position of (x,y), respectively, and χ(x) is a step function that χ(x)=0 for x ≤0 and χ(x)=1 for x>0. f(x−α/2, y) and f(x+α/2, y) represent the N-photon probability densities in the horizontal and vertical polarization modes written as

After passing through the second calcite crystal, the two beams are displaced at a distance of −α/2 for H polarization and α/2 for V polarization along the x axis, resulting in two beams in the same spatial mode. The state can then be written as

Here, we assume that the state is projected onto the state where odd number of photons are in the minus diagonal polarization mode at the output. The measurement operator in the basis of plus (P) and minus (M) diagonal polarization is therefore written as

where

The probability of odd number photon detection can then be written as

where we denote the phase-independent term of 
 as ξ(α) which is the overlap integral between H and V polarized beams at the sample plane.
as ξ(α) which is the overlap integral between H and V polarized beams at the sample plane.
We now calculate the SNR of our microscope using the NOON state including the effect of the overlap between the two beams at the sample plane. If the emission of the N-photon states is statistically independent, the statistical noise at the bias phase  is given by
is given by

For a small positive phase shift of  , the signal is
, the signal is

Considering the visibility of the interference fringe VN, the SNR is given by

Thus one can confirm that counting odd (or even) number photon-detection events can also achieve the phase super sensitivity. Note also that the dependence of SNR on the size and the distance between the two beams is simply given by (1−ξ). This means that it is reasonable to compare the SNR between an entanglement-enhanced microscope and a classical microscope (N=1) for the same ξ.
Additional information
How to cite this article: Ono, T. et al. An entanglement-enhanced microscope. Nat. Commun. 4:2426 doi: 10.1038/ncomms3426 (2013).
References
Giovannetti, V., Lloyd, S. & Maccone, L. Quantum-enhanced measurements: beating the standard quantum limit. Science 306, 1330–1336 (2004).
Meyer, V. et al. Experimental demonstration of entanglement-enhanced rotation angle estimation using trapped ions. Phys. Rev. Lett. 86, 5870–5873 (2001).
Leibfried, D. et al. Creation of a six-atom ‘Schrodinger cat' state. Nature 438, 639–642 (2005).
Roos, C. F., Chwalla, M., Kim, K., Riebe, M. & Blatt, R. Designer atoms' for quantum metrology. Nature 443, 316–319 (2006).
Widera, A. et al. Entanglement interferometry for precision measurement of atomic scattering properties. Phys. Rev. Lett. 92, 160406 (2004).
Rarity, J. G. et al. Two-photon interference in a Mach-Zehnder interferometer. Phys. Rev. Lett. 65, 1348–1351 (1990).
Kuzmich, A. & Mandel, L. Sub-shot-noise interferometric measurements with two-photon states. Quant. Semiclass. Opt. 10, 493–500 (1998).
Fonseca, E., Monken, C. & Padua, S. Measurement of the de Broglie wavelength of a multiphoton wave packet. Phys. Rev. Lett. 82, 2868–2871 (1999).
Edamatsu, K., Shimizu, R. & Itoh, T. Measurement of the photonic de Broglie wavelength of entangled photon pairs generated by spontaneous parametric down-conversion. Phys. Rev. Lett. 89, 213601 (2002).
Eisenberg, H., Hodelin, J., Khoury, G. & Bouwmeester, D. Multiphoton path entanglement by nonlocal bunching. Phys. Rev. Lett. 94, 090502 (2005).
Nagata, T., Okamoto, R., O'brien, J. L., Sasaki, K. & Takeuchi, S. Beating the standard quantum limit with four-entangled photons. Science 316, 726–729 (2007).
Okamoto, R. et al. Beating the standard quantum limit: phase super-sensitivity of N-photon interferometers. New J. Phys. 10, 073033 (2008).
Xiang, G. Y., Higgins, B. L., Berry, D. W., Wiseman, H. M. & Pryde, G. J. Entanglement-enhanced measurement of a completely unknown optical phase. Nat. Photon. 5, 43–47 (2010).
Crespi, A. et al. Measuring protein concentration with entangled photons. Appl. Phys. Lett. 100, 233704 (2012).
Wolfgramm, F., Vitelli, C., Beduini, F. A., Godbout, N. & Mitchell, M. W. Entanglement-enhanced probing of a delicate material system. Nat. Photon. 7, 28–32 (2013).
Taylor, M. A. et al. Biological measurement beyond the quantum limit. Nat. Photon. 7, 229–233 (2013).
Nomarski, M. G. Microinterféromètre différentiel à ondes polarisées. J. Phys. Radium 16, 9S (1955).
Jesorka, A. et al. Generation of phospholipid vesicle-nanotube networks and transport of molecules therein. Nat. Protoc. 6, 791–805 (2011).
Sazaki, G., Zepeda, S., Nakatsubo, S., Yokoyama, E. & Furukawa, Y. Elementary steps at the surface of ice crystals visualized by advanced optical microscopy. Proc. Natl Acad. Sci. USA 107, 19702–19707 (2010).
Sazaki, G., Zepeda, S., Nakatsubo, S., Yokoyama, E. & Furukawa, Y. Quasi-liquid layers on ice crystal surfaces are made up of two different phases. Proc. Natl Acad. Sci. USA 109, 1052–1055 (2012).
Gerry, C. Heisenberg-limit interferometry with four-wave mixers operating in a nonlinear regime. Phys. Rev. A 61, 043811 (2000).
Seshadreesan, K. P., Kim, S., Dowling, J. P. & Lee, H. Phase estimation at the quantum Cramer-Rao bound via parity detection. Phys. Rev. A 87, 043833 (2013).
Kwiat, P. G., Waks, E., White, A. G., Appelbaum, I. & Eberhard, P. H. Ultrabright source of polarization-entangled photons. Phys. Rev. A 60, R773–R776 (1999).
White, A. G., James, D. F. V., Eberhard, P. H. & Kwiat, P. G. Nonmaximally entangled states: production, characterization, and utilization. Phys. Rev. Lett. 83, 3103–3107 (1999).
Kawabe, Y., Fujiwara, H., Okamoto, R., Sasaki, K. & Takeuchi, S. Quantum interference fringes beating the diffraction limit. Opt. Express 15, 14244–14250 (2007).
Teich, M. C. & Saleh, B. E. A. Entangled-photon microscopy. Ceskoslovensky Casopis Pro Fyziku 47, 3–8 (1997)) English translation is available at http://people.bu.edu/teich/pdfs/Cesk-English-47-3-1997.pdf(1997).
Boto, A. N. et al. Quantum interferometric optical lithography: exploiting entanglement to beat the diffraction limit. Phys. Rev. Lett. 85, 2733–2736 (2001).
D’Angelo, M., Chekhova, M. & Shih, Y. Two-photon diffraction and quantum lithography. Phys. Rev. Lett. 87, 013602 (2001).
Pittman, T. B., Shih, Y. H., Strekalov, D. V. & Sergienko, A. V. Quantum interferometric optical lithography: exploiting entanglement to beat the diffraction limit. Phys. Rev. A 52, R3429–R3432 (1995).
Giovannetti, V., Lloyd, S. & Maccone, L. Quantum metrology. Phys. Rev. Lett. 96, 010401 (2006).
Ou, L. H. & Kuang, L. M. Ghost imaging with third-order correlated thermal light. J. Phys. B: At. Mol. Opt. Phys. 40, 1833–1844 (2007).
Cao, D. Z. et al. Enhancing visibility and resolution in Nth-order intensity correlation of thermal light. Appl. Phys. Lett. 92, 201102 (2008).
Liu, Q., Chen, X. H., Luo, K. H., Wu, W. & Wu, L. A. Role of multiphoton bunching in high-order ghost imaging with thermal light sources. Phys. Rev. A 79, 053844 (2009).
Chan, K. W. C., O'Sullivan, M. N. & Boyd, R. W. High-order thermal ghost imaging. Opt. Lett. 34, 3343–3345 (2009).
Chan, K. W. C., Sullivan, M. N. O. & Boyd, R. W. Optimization of thermal ghost imaging: high-order correlations vs. background subtraction. Opt. Express 18, 5562–5573 (2010).
Chen, X. H. et al. High-visibility, high-order lensless ghost imaging with thermal light. Opt. Lett. 35, 1166–1168 (2010).
Cao, B. & Zhang, C. Third-order lensless ghost diffraction with classical fully incoherent light. Opt. Lett. 35, 2091–2093 (2010).
Takeuchi, S., Kim, J., Yamamoto, Y. & Hogue, H. H. Development of a high-quantum-efficiency single-photon counting system. Appl. Phys. Lett. 74, 1063–1065 (1999).
Fukuda, D. et al. Titanium-based transition-edge photon number resolving detector with 98% detection efficiency with index-matched small-gap fiber coupling. Opt. Express 19, 870–875 (2011).
Goda, K. et al. A quantum-enhanced prototype gravitational-wave detector. Nat. Phys. 4, 472–476 (2008).
Anisimov, P. M. et al. Quantum metrology with two-mode squeezed vacuum: parity detection beats the Heisenberg limit. Phys. Rev. Lett. 104, 103602 (2010).
Ono, T. & Hofmann, H. F. Effects of photon losses on phase estimation near the Heisenberg limit using coherent light and squeezed vacuum. Phys. Rev. A 81, 033819 (2010).
Okamoto, R. et al. Experimental demonstration of adaptive quantum state estimation. Phys. Rev. Lett. 109, 130404 (2012).
Hannemann, T. h. et al. Self-learning estimation of quantum states. Phys. Rev. A 65, 050303 (2002).
James, D. F. V., Kwiat, P. G., Munro, W. J. & White, A. G. Measurement of qubits. Phys. Rev. A 64, 080504 (2001).
Acknowledgements
We thank Dr. Shouichi Sakakihara for sample fabrication, Professor Hidekazu Tanaka and Dr. Koichi Okada for atomic force microscope measurements. We also thank Professor Mitsuo Takeda, Professor Yoko Miyamoto, Professor Gen Sazaki, Professor Holger F. Hofmann and Professor Masamichi Yamanishi for helpful discussion. This work was supported in part by FIRST of JSPS, Quantum Cybernetics of JSPS, a Grant-in-Aid from JSPS, JST-CREST, Special Coordination Funds for Promoting Science and Technology, Research Foundation for Opto-Science and Technology and the GCOE programme.
Author information
Authors and Affiliations
Contributions
Experiments, measurements and data analysis were performed by T.O. with assistance of R.O. and S.T. The project was planned by S.T. and supervised by R.O. and S.T. The manuscript was written by all the authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Ono, T., Okamoto, R. & Takeuchi, S. An entanglement-enhanced microscope. Nat Commun 4, 2426 (2013). https://doi.org/10.1038/ncomms3426
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms3426
This article is cited by
-
Quantum hyper-entangled system with multiple qubits based on spontaneous parametric down-conversion and birefringence effect
Optical and Quantum Electronics (2024)
-
Quantum enhanced non-interferometric quantitative phase imaging
Light: Science & Applications (2023)
-
Speed limit of quantum metrology
Scientific Reports (2023)
-
Modeling the space-time correlation of pulsed twin beams
Scientific Reports (2023)
-
Applications of single photons in quantum metrology, biology and the foundations of quantum physics
Nature Reviews Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.