Abstract
Superconducting circuits with Josephson junctions are promising candidates for developing future quantum technologies. Of particular interest is to use these circuits to study effects that typically occur in complex condensed-matter systems. Here we employ a superconducting quantum bit—a transmon—to perform an analogue simulation of motional averaging, a phenomenon initially observed in nuclear magnetic resonance spectroscopy. By modulating the flux bias of a transmon with controllable pseudo-random telegraph noise we create a stochastic jump of its energy level separation between two discrete values. When the jumping is faster than a dynamical threshold set by the frequency displacement of the levels, the initially separate spectral lines merge into a single, narrow, motional-averaged line. With sinusoidal modulation a complex pattern of additional sidebands is observed. We show that the modulated system remains quantum coherent, with modified transition frequencies, Rabi couplings, and dephasing rates. These results represent the first steps towards more advanced quantum simulations using artificial atoms.
Similar content being viewed by others
Introduction
The ability to resolve energy variations ΔE occurring in a time interval Δt is fundamentally limited by the energy-time uncertainty relation  . Consider for example a system of spin-1/2 particles filling a porous material (Fig. 1a) in an external magnetic field; then, if the pore wall is paramagnetic, the particles near it will experience a modified local magnetic field. As a result, static particles will produce two spectral peaks in the nuclear magnetic resonance spectrum at frequencies ω1 and ω2 (Fig. 1b). In contrast, particles moving swiftly back and forth between the two regions on timescales Δt shorter than
. Consider for example a system of spin-1/2 particles filling a porous material (Fig. 1a) in an external magnetic field; then, if the pore wall is paramagnetic, the particles near it will experience a modified local magnetic field. As a result, static particles will produce two spectral peaks in the nuclear magnetic resonance spectrum at frequencies ω1 and ω2 (Fig. 1b). In contrast, particles moving swiftly back and forth between the two regions on timescales Δt shorter than  are not able to discriminate between the two energy values. Then, as the particles move faster, the outcome in the spectroscopy is not simply a continuous broadening and overlapping of the two peaks. Instead, a new peak emerges at the average frequency ω0 with a width smaller than the energy separation
are not able to discriminate between the two energy values. Then, as the particles move faster, the outcome in the spectroscopy is not simply a continuous broadening and overlapping of the two peaks. Instead, a new peak emerges at the average frequency ω0 with a width smaller than the energy separation  , denoted as motional averaging and narrowing1,2, respectively. In atomic ensembles and condensed-matter systems, this occurs via fast variations of the electronic state populations, chemical potential, molecular conformation, effective magnetic fields, lattice vibrations, micro-electric fields producing ac-Stark shifts and so on1,2,3,4,5,6. Closely related phenomena are the Dyakonov-Perel effect7, the Dicke line narrowing of Doppler spectra8, and the quantum Zeno effect9.
, denoted as motional averaging and narrowing1,2, respectively. In atomic ensembles and condensed-matter systems, this occurs via fast variations of the electronic state populations, chemical potential, molecular conformation, effective magnetic fields, lattice vibrations, micro-electric fields producing ac-Stark shifts and so on1,2,3,4,5,6. Closely related phenomena are the Dyakonov-Perel effect7, the Dicke line narrowing of Doppler spectra8, and the quantum Zeno effect9.
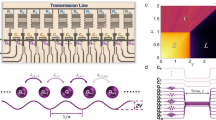
(a) Illustration of a single pore filled with a medium consisting of spin-1/2 particles that are either static or moving. White and grey areas denote different magnetic environments, producing the energy splittings  and
and  , respectively (see b,c). (b) Schematic spectrum of the motional averaging. The solid lines denote the spectrum of static particles, while the dashed line corresponds to moving particles. (c) A sample trajectory of the energy splitting
, respectively (see b,c). (b) Schematic spectrum of the motional averaging. The solid lines denote the spectrum of static particles, while the dashed line corresponds to moving particles. (c) A sample trajectory of the energy splitting  in equation (1). (d) Schematic diagram of the sample device and the simplified experimental set-up. Two asymmetric Josephson junctions (EJ1 and EJ2) are capacitively shunted (CB) and coupled (CG) to a resonator. The time-dependent transition frequency of the qubit is controlled with fast flux pulses on top of a dc bias (Iflux=Idc+Ipulse), generated by an AWG. A vector network analyser (VNA) is used for probing the resonator at ωprobe≈ωr. One microwave source (ω) is used for driving the qubit. Additional details are shown in Methods and in Supplementary Fig. S1.
in equation (1). (d) Schematic diagram of the sample device and the simplified experimental set-up. Two asymmetric Josephson junctions (EJ1 and EJ2) are capacitively shunted (CB) and coupled (CG) to a resonator. The time-dependent transition frequency of the qubit is controlled with fast flux pulses on top of a dc bias (Iflux=Idc+Ipulse), generated by an AWG. A vector network analyser (VNA) is used for probing the resonator at ωprobe≈ωr. One microwave source (ω) is used for driving the qubit. Additional details are shown in Methods and in Supplementary Fig. S1.
In this paper, we report the observation of motional averaging and narrowing in a single artificial atom, a quantum bit (qubit), with a simulated fast-fluctuating environment under direct experimental control. This should be contrasted with the typical situation in condensed-matter systems, where one has a large number of particles and the experimentalist can only indirectly attempt to change the fluctuation rate, typically by modifying a thermodynamic function of state, such as temperature or pressure.
Results
Frequency-modulated transmon qubit
Our device is a circuit QED system10, consisting of a tunable transmon coupled to a quarter-wavelength coplanar waveguide resonator. The circuit schematic and the simplified experimental set-up are shown in Fig. 1d and in Supplementary Fig. S1. The applied bias flux Φ through the qubit loop consists of a constant part Φdc and a time-dependent part Φac(t) with an amplitude much smaller than Φdc. The Hamiltonian of the transmon qubit11 is

where  . Here Φ0=h/2e is the magnetic flux quantum, the Josephson plasma frequency is
. Here Φ0=h/2e is the magnetic flux quantum, the Josephson plasma frequency is  ,
,  denote the Pauli matrices, the single-electron charging energy is EC=e2/2(CG+CB)≈h × 0.35 GHz, EJ=EJ1+EJ2≈24EC is the maximum Josephson energy, and d=(EJ1−EJ2)/EJ≈0.11 denotes the junction asymmetry. We choose Φdc so that ω0/2π=2.62 GHz, which is far detuned from the bare resonator frequency ωr/2π=3.795 GHz, allowing the dispersive measurement of the qubit through the resonator by standard homodyne and heterodyne techniques12.
denote the Pauli matrices, the single-electron charging energy is EC=e2/2(CG+CB)≈h × 0.35 GHz, EJ=EJ1+EJ2≈24EC is the maximum Josephson energy, and d=(EJ1−EJ2)/EJ≈0.11 denotes the junction asymmetry. We choose Φdc so that ω0/2π=2.62 GHz, which is far detuned from the bare resonator frequency ωr/2π=3.795 GHz, allowing the dispersive measurement of the qubit through the resonator by standard homodyne and heterodyne techniques12.
The time-dependent part  of the energy splitting, determined by Φac(t), is controlled by an arbitrary waveform generator (AWG) via a fast flux line. The random telegraph noise (RTN) is realized by feeding pseudo-random rectangular pulses to the on-chip flux bias coil. Ideally, the dynamics of
of the energy splitting, determined by Φac(t), is controlled by an arbitrary waveform generator (AWG) via a fast flux line. The random telegraph noise (RTN) is realized by feeding pseudo-random rectangular pulses to the on-chip flux bias coil. Ideally, the dynamics of  is a stationary, dichotomous Markovian process, characterized by an average jumping rate χ and symmetrical dwellings at frequency values of ±ξ (see Fig. 1c). The number of jumps is a Poisson process with the probability Pn(t)=(χt)ne−χt/n! for exactly n jumps within a time interval t. This Poissonian process simulates the temporal variations causing motional averaging in atomic ensembles and condensed-matter systems (Fig. 1).
is a stationary, dichotomous Markovian process, characterized by an average jumping rate χ and symmetrical dwellings at frequency values of ±ξ (see Fig. 1c). The number of jumps is a Poisson process with the probability Pn(t)=(χt)ne−χt/n! for exactly n jumps within a time interval t. This Poissonian process simulates the temporal variations causing motional averaging in atomic ensembles and condensed-matter systems (Fig. 1).
Simulation of motional averaging
In order to find the effective transition energies and decoherence rates of the modulated system, we calculate the absorption spectrum1,2. For a qubit subjected to RTN fluctuations as in equation (1), we exploit the quantum regression theorem13 to find the spectrum (see details in Supplementary Note S1)

where the expectation value is taken over noise realizations and Γ2=Γϕ+Γ1/2 is the decoherence rate in the absence of modulation. For our sample Γ2≈2π × 3 MHz (determined in an independent measurement). For the Poisson process ξ(t), equation (2) gives1,2,14,15

with  and
and  . In our measurement, we have recorded the population of qubit's excited state, as shown in Fig. 2 and in Supplementary Fig. S2. The qubit is excited with a transverse drive
. In our measurement, we have recorded the population of qubit's excited state, as shown in Fig. 2 and in Supplementary Fig. S2. The qubit is excited with a transverse drive
(a) Numerical simulation of the occupation probability Pe plotted in the ω−χ plane with parameters ξ/2π=43 MHz, g/2π=8 MHz, Γ1/2π=1 MHz, and Γ2/2π=3 MHz. (b) Measured excited state occupation probability Pe under the RTN modulation. (c) Horizontal cuts of the measured occupation probability in b, denoted with white lines, at three different jumping rates (solid lines). For clarity, the curves are displaced vertically by 0.3. The dashed lines indicate the corresponding results of the numerical simulation in a. See Supplementary Fig. S2 for the zero-detuning (ω=ω0) occupation probability Pe with different ξ.

The simulation of the occupation probability presented in Fig. 2a (see Methods and Supplementary Note S2) includes also the effect of power broadening due to strong driving amplitudes (g>Γ1,Γ2).
Two intuitively appealing limits result from equation (3) (see also Fig. 2) at the opposite sides of a dynamical threshold defined by χ=ξ. In the case of slow jumping,  , and resolvable energy variations,
, and resolvable energy variations,  , the qubit absorbs energy at ω0±ξ with the total decoherence rate
, the qubit absorbs energy at ω0±ξ with the total decoherence rate  . The correlation time of the displacement process
. The correlation time of the displacement process  is τξ=(2χ)−1 and the linewidth (full width at half maximum
is τξ=(2χ)−1 and the linewidth (full width at half maximum  ) broadens by the amount of the reduced mean life-time of a qubit excitation (exchange broadening1). In contrast, for fast jumping processes,
) broadens by the amount of the reduced mean life-time of a qubit excitation (exchange broadening1). In contrast, for fast jumping processes,  , and when the variations are not resolvable,
, and when the variations are not resolvable,  , the qubit absorbs energy only at the frequency ω0 with
, the qubit absorbs energy only at the frequency ω0 with  . The increase in decoherence rate by ξ2/2χ can be related to the excursions of the accumulated phase
. The increase in decoherence rate by ξ2/2χ can be related to the excursions of the accumulated phase  (equation (2)) for single noise realizations, especially to the diffusion coefficient of the process16. Surprisingly, the averaged spectral line is well-localized around the mean value, since
(equation (2)) for single noise realizations, especially to the diffusion coefficient of the process16. Surprisingly, the averaged spectral line is well-localized around the mean value, since  . The effect of motional narrowing can be best seen in Fig. 2c as a raise in the height of the centre peak because the additional decoherence ξ2/2χ decreases with increasing jumping rate χ. When χ is comparable with ξ, there is a cross-over region where absorption is reduced and the peak broadens due to enhanced decoherence (see Fig. 2). This is important for the improvement of qubit dephasing times as it implies that a longitudinally coupled two-level system (TLS) fluctuator is the most poisonous when its internal dynamics occurs approximately at the same frequency as the coupling to the qubit.
. The effect of motional narrowing can be best seen in Fig. 2c as a raise in the height of the centre peak because the additional decoherence ξ2/2χ decreases with increasing jumping rate χ. When χ is comparable with ξ, there is a cross-over region where absorption is reduced and the peak broadens due to enhanced decoherence (see Fig. 2). This is important for the improvement of qubit dephasing times as it implies that a longitudinally coupled two-level system (TLS) fluctuator is the most poisonous when its internal dynamics occurs approximately at the same frequency as the coupling to the qubit.
A counter-intuitive aspect of motional averaging is that the system is at any time in either one of the states  and spends no time in-between. Yet spectroscopically it is not seen in the states
and spends no time in-between. Yet spectroscopically it is not seen in the states  ; instead it has a clear signature in the middle. Also, the spectrum (3) decays as 1/ω4 far in the wings, showing a non-Lorentzian character that originates from the non-exponential decay of the correlator
; instead it has a clear signature in the middle. Also, the spectrum (3) decays as 1/ω4 far in the wings, showing a non-Lorentzian character that originates from the non-exponential decay of the correlator  14. This is because the frequent
14. This is because the frequent  -changes have a similar effect to a continuous measurement of the system, slowing its dynamics in analogy with the quantum Zeno effect9,17.
-changes have a similar effect to a continuous measurement of the system, slowing its dynamics in analogy with the quantum Zeno effect9,17.
Sinusoidal modulation of frequency
To further explore these effects, we have used sinusoidal waves to modulate the qubit energy splitting:  . In Fig. 3a, the experimental data and the corresponding numerical simulation are shown. Resolved sidebands appear at ω=ω0±kΩ (k=0,1,2,…), and are amplitude-modulated with Bessel functions Jk(δ/Ω), where δ and Ω denote the modulation amplitude and frequency, respectively. The Hamiltonian
. In Fig. 3a, the experimental data and the corresponding numerical simulation are shown. Resolved sidebands appear at ω=ω0±kΩ (k=0,1,2,…), and are amplitude-modulated with Bessel functions Jk(δ/Ω), where δ and Ω denote the modulation amplitude and frequency, respectively. The Hamiltonian  (equations (1) and (4)) can be transformed to a non-uniformly rotating frame18,19 (see Methods). The theoretical prediction for the steady-state occupation probability on the resolved sidebands (Ω>g>Γ2) is
(equations (1) and (4)) can be transformed to a non-uniformly rotating frame18,19 (see Methods). The theoretical prediction for the steady-state occupation probability on the resolved sidebands (Ω>g>Γ2) is
(a) Measured excited state occupation probability Pe with amplitude δ/2π=250 MHz. (b) Simulation with Γ1/2π=1 MHz, Γ2/2π=3 MHz, and g/2π=20 MHz. c The cut along the dashed line in a,b at Ω/2π=210 MHz. The (black) circles are the experimental data. The (blue) line denotes the analytical occupation probability obtained from equation (5) by taking k=−1,0,1, which overlaps perfectly with the simulation in the parameter regime,  . For k=0 (0-band), the linewidth is narrower than the bare linewidth without modulation (see Methods and Supplementary Fig. S3).
. For k=0 (0-band), the linewidth is narrower than the bare linewidth without modulation (see Methods and Supplementary Fig. S3).

which is compared with experimental data in Fig. 3c and in Supplementary Fig. S3. These population oscillations can be alternatively understood as a photon-assisted version of the standard Landau–Zener–Stückelberg interference20,21 (see Methods and Supplementary Fig. S4). Also, when the qubit drive is tuned close to the resonator frequency ω≈ωr and when the driving amplitude g is large and equal to the frequency of the modulation g=Ω, the system can be seen as a realization of a quantum simulator of the ultrastrong coupling regime22,23. In our set-up, the simulated coupling rate is estimated to reach over 10% of the effective resonator frequency (see Supplementary Note S3), comparable to earlier reports24,25 where the ultrastrong coupling was obtained by sample design. The sinusoidal modulation allows a different perspective on motional averaging. The RTN noise comprises many different modulation frequencies Ω (Fig. 1c). Each frequency creates different sidebands (k=1,2,3,…), which overlap and average away. At large Ω's only the central band k=0 survives because the only non-vanishing Bessel function of zero argument is J0(0)=1.
Coherence of the modulated system
Finally, we show that it is possible to use the modulated system as a new, photon-dressed qubit. Indeed, we can drive Rabi oscillations on the central band and on the resolved sidebands (see Fig. 4 and Supplementary Fig. S5). For fast RTN modulation,  , and under the strong drive in equation (4), we construct (see Supplementary Note S2) a master equation15 describing the Rabi-oscillation with the detuned Rabi frequency
, and under the strong drive in equation (4), we construct (see Supplementary Note S2) a master equation15 describing the Rabi-oscillation with the detuned Rabi frequency  and with the total decoherence rate
and with the total decoherence rate  . In the case of sinusoidal modulation, the Rabi frequencies on the sidebands are obtained as
. In the case of sinusoidal modulation, the Rabi frequencies on the sidebands are obtained as  .
.
(a) Rabi oscillations versus driving frequency with RTN modulation: measurement and numerical simulation with ω0/2π=2.610 GHz, ξ/2π≈95 MHz, χ≈600 MHz, g/2π=91 MHz, Γ1/2π=1 MHz, and Γ2/2π=3 MHz. The corresponding Rabi oscillations in the case of sinusoidal modulation are shown in Supplementary Fig. S5. (b) The measured Rabi frequency of the random and sinusoidal modulation g and geff, respectively, as a function of Rabi-pulse amplitude (same scaling in the both panels). The solid and dashed lines are fits to the data in the linear regime. (c) Rabi frequencies versus amplitude of the sinusoidal modulation. The horizontal axis is the dimensionless scaled modulation amplitude δ/Ω, which is also the argument for the effective Rabi frequency  plotted with g/2π=60 MHz and colour coding for k: 0 (red dotted) and 1 (blue dashed). The (red) circles and (blue) triangles indicate the measured Rabi frequencies at the centre of 0-band and 1-band, respectively.
plotted with g/2π=60 MHz and colour coding for k: 0 (red dotted) and 1 (blue dashed). The (red) circles and (blue) triangles indicate the measured Rabi frequencies at the centre of 0-band and 1-band, respectively.
Discussion
Our work could open up several research directions. For example, a key limitation in solid-state based quantum processing of information is the decoherence due to fluctuating TLSs in the dielectric layers fabricated on-chip26,27,28. We anticipate, resting on the motional narrowing phenomenon, that the dephasing times of the existing superconducting qubits may be dramatically improved if one is able to accelerate the dynamics of the longitudinally coupled TLSs. The quantum coherence of the resolved sidebands and of the central band suggest that low-frequency modulation offers an additional tool for implementing quantum gates29, in analogy with the use of vibrational sidebands in the ion trap computers30. Also, if the two tones used to drive and modulate the qubit satisfy certain conditions, the system can be mapped into an effective qubit-harmonic oscillator system with ultrastrong coupling, opening this regime for experimental investigations. Finally, the recent progress in the field of nanomechanical oscillators makes possible the study of frequency jumps in nanomechanical resonators16, which is predicted to be accompanied by squeezing31. Our work paves the way for further simulations of quantum coherence phenomena using superconducting quantum circuits32,33.
Methods
Measurement set-up
The electronic measurement set-up at room temperature is illustrated in Supplementary Fig. S1. For qubit spectroscopy with RTN modulations, the dc flux bias and RTN modulations are generated by an Agilent 81150A AWG. The qubit driving signal from an Agilent E8257D analogue signal generator and the coplanar waveguide cavity probe signal from an Agilent N5230C PNA-L network analyser are combined together by a Mini-Circuits ZFSC-2-10G power splitter/combiner and sent to the cavity input line of the dilution refrigerator. The signal from the cavity output line of the dilution refrigerator is amplified and detected by a PNA-L network analyser. For sinusoidal modulations, the tones are generated by a R&S SMR27 microwave signal generator and they are added to the dc bias generated by the Agilent 81150A via a bias tee (not shown). Between the radio frequency instruments (analogue signal generator and network analyser) and their corresponding lines, dc blocks are used for breaking possible ground loops. All instruments are synchronized with a SRS FS725 Rubidium frequency standard (not shown in the figure).
For Rabi-oscillation measurements, high ON/OFF ratio Rabi pulses are generated by mixing a continuous microwave signal from the Agilent E8257D with rectangular pulses from a SRS DG645 digital delay generator via two identical Mini-Circuits frequency mixers. The Agilent N5230C PNA-L is used as a signal generator. Its output signal is split into two parts. One part is used for generating measurement pulses in a similar fashion to the Rabi pulses; the other part acts as a local oscillator signal to mix the output signal from the coplanar waveguide cavity down via a Marki IQ mixer. The IQ data is filtered, amplified by a SRS SR445A pre-amplifier, and digitized by an Agilent U1082A-001 digitiser.
Measurement controlling and data processing are done by MATLAB running on a measurement computer. The communication between the measurement computer and the instruments is realized through IEEE-488 GPIB buses. To generate RTN pulses, we use MATLAB’s internal Poisson random number generator poissrnd(λ) to obtain binary RTN sequences, and load the sequences into the Agilent 81150A AWG. Each binary RTN sequence consists of 50,000 data points and around 5,000 random jumps in average. The mean jumping rate χ (of AWG's output) is modulated by changing the clock frequency ν of the AWG: χ≈5,000 × ν. To verify this relation between χ and ν, we observe the RTN sequences at different ν's by a fast oscilloscope (10 GS per s), count the number n of edges (jumping events) for certain period of time t, and calculate the real mean jumping rate by its original definition, χ=n/t. As an example, a 0.5-μs long RTN sequence with estimated mean jumping rate χ≈5,000 × 10 KHz=50 MHz is shown in Supplementary Fig. S1. Twenty-five jumps are counted during 0.5 μs, which gives χ=50 MHz. As long as ν<100 KHz, the formula χ≈5,000 × ν gives a good estimation of the mean jumping rate. For ν>100 KHz, the real mean jumping rate is smaller than the estimated one, due to the intrinsic ∼2 ns rising/falling time of the AWG.
Numerical simulations
The occupation probability of Figs 2a, c, 3b, and Supplementary Figs S2 and S4 is a result of solving numerically the master equation

in the frame rotating at ω and applying the rotating wave approximation (the pure dephasing rate Γϕ=Γ2−Γ1/2). For the random modulation (Figs 2a, c, and Supplementary Fig. S2), we apply the method of quantum trajectories13 and the imperfections of the experimentally realized wave forms (the raising/falling time ∼2.0 ns and the sampling time 0.5 ns) are included in the simulation.
Multi-photon transition process in sinusoidal modulation
The effects of sinusoidally modulating the transition frequency of an atom is a generic problem in theoretical physics, and has attracted a lot of interest in the past, most notably in the quantum-optics community34,35. We address now this problem in the context of superconducting qubits. We consider a transmon qubit whose energy splitting is modulated sinusoidally:  . Even though
. Even though  , the qubit can be excited with the low-frequency signal in the presence of an additional high-frequency drive ω. This can be seen as a multi-photon transition process involving quanta from both fields (in equation (5)), or, as a photon-assisted Landau–Zener–Stückelberg (LZS) interference18,20,21,36 between the dressed states |↓, n〉 and |↑, n−1〉.
, the qubit can be excited with the low-frequency signal in the presence of an additional high-frequency drive ω. This can be seen as a multi-photon transition process involving quanta from both fields (in equation (5)), or, as a photon-assisted Landau–Zener–Stückelberg (LZS) interference18,20,21,36 between the dressed states |↓, n〉 and |↑, n−1〉.
Let us first consider the multi-photon transition processes associated with the sinusoidal-modulated Hamiltonian, defined in equations (1) and (4),

The qubit is driven both in the longitudinal ( ) and in the transverse (
) and in the transverse ( ) direction. We show below how to eliminate the time-dependence from the longitudinal drive. After moving to a non-uniformly rotating frame with the unitary transformation18,19
) direction. We show below how to eliminate the time-dependence from the longitudinal drive. After moving to a non-uniformly rotating frame with the unitary transformation18,19

the effective Hamiltonian is  , and by using the Jacobi-Anger relations, we get
, and by using the Jacobi-Anger relations, we get

By assuming that the transverse drive is close to a resonance, that is, ω≈ω0±kΩ (k=0,1,2…) and that the resonances are resolvable Ω>g>Γ2, we transform back with  and ignore all but the resonant terms, that is, all the fast rotating terms (rotating wave approximation, RWA). The resulting RWA Hamiltonian reads
and ignore all but the resonant terms, that is, all the fast rotating terms (rotating wave approximation, RWA). The resulting RWA Hamiltonian reads

describing, in the Bloch spin representation, precessions around the vector Ω=(gJk(δ/Ω),0,ω0+kΩ−ω) with the effective Rabi frequency

Exactly at the multi-photon resonance ω=ω0±kΩ (k=0,1,2…), the effective Rabi frequency is |gJk(δ/Ω)|, and it is plotted in Fig. 4c.
In the time domain, the measured Rabi oscillations are presented in Supplementary Fig. S5 together with numerical simulations of Bloch equations exploiting the effective Rabi frequency in equation (11). To find the steady-state occupation probability in the presence of relaxation with rate Γ1 and decoherence with rate Γ2, we solve the Bloch equations analytically. In the RWA, that is when Ω>g>Γ2 is satisfied, one is allowed to add up independent contributions from all the resonances (the resolved sidebands). The result for the steady-state excited state occupation probability is equation (5). In the non-modulated case, the corresponding expression for the occupations is simply

The occupation probabilities in equations (5) and (12) are compared with the experimental steady-state occupation probabilities in Supplementary Fig. S3. An interesting effect is that the linewidth of the modulated qubit on the central band is always smaller than the linewidth on the qubit in the absence of the modulation due to reduced power broadening.
Photon-assisted Landau–Zener–Stückelberg interference
The spectra seen in the experiment under sinusoidal modulation can be also interpreted as a photon-assisted LZS effect. Note that in the absence of the driving field standard LZS processes are not possible: indeed the qubit energy separation is one order of magnitude higher than the modulation frequency, therefore the standard LZS probability is negligibly small. However, the system can still perform LZS transitions by absorbing a photon from the driving field. This photon-assisted LZS interference can be seen by transforming the Hamiltonian  from equation (7) into the frame rotating at ω around the z axis (unitary transformation
from equation (7) into the frame rotating at ω around the z axis (unitary transformation  ), where it has exactly the same form (in the RWA) as that of LZS interference18,21,36, namely
), where it has exactly the same form (in the RWA) as that of LZS interference18,21,36, namely

As illustrated in Supplementary Fig. S4, LZS transition events may occur when the modulation amplitude δ is of the order of, or larger than, the detuning between the driving frequency and the qubit splitting ω–ω0. The LZS transitions occur between the transversely dressed states |↓, n〉 and |↑, n−1〉, where n refers to the photon number of the transverse driving field. The phase difference of the two states gathered between the consecutive tunnelling events leads to either constructive or destructive interference observed as maxima or minima in the occupation probability of the excited state, shown in Supplementary Fig. S4. The LZS interference seen in our system corresponds to the so-called fast passage limit21. In this limit, the expression for the occupation probability can be calculated analytically21 and the result agrees exactly with our equation (5).
To prove experimentally that this picture is valid, we have scanned the modulation amplitude δ and the driving frequency ω at fixed Ω. We observe an interference pattern of the steady-state occupation probability, which is in good agreement with the theoretical prediction, see Supplementary Fig. S4.
Additional information
How to cite this article: Li. J. et al. Motional averaging in a superconducting qubit. Nat. Commun. 4:1420 doi: 10.1038/ncomms2383 (2013).
References
Anderson, P. W. . A mathematical model for the narrowing of spectral lines by exchange or motion. J. Phys. Soc. Jpn. 9, 316–339 (1954) .
Abragam, A. . Principles of Nuclear Magnetism Oxford University Press (1986) .
Jiang, L. et al. Coherence of an optically illuminated single nuclear spin qubit. Phys. Rev. Lett. 100, 073001 (2008) .
Kohmoto, T. et al. Hole burning in well-defined noise fields: motional narrowing. Phys. Rev. B 49, 15352–15355 (1994) .
Berthelot, A. et al. Unconventional motional narrowing in the optical spectrum of a semiconductor quantum dot. Nat. Phys. 2, 759–764 (2006) .
Sagi, Y., Pugatch, R., Almog, I. & Davidson, N. . Spectrum of two-level systems with discrete frequency fluctuations. Phys. Rev. Lett. 104, 253003 (2010) .
D'yakonov, M. I. & Perel’, V. I. . Spin relaxation of conduction electrons in noncentrosymmetric semiconductors. Sov. Phys. Solid State 13, 3023–3026 (1972) .
Dicke, R. H. . The effect of collisions upon the Doppler width of spectral lines. Phys. Rev. 89, 472–473 (1953) .
Milburn, G. J. . Quantum Zeno effect and motional narrowing in a two-level system. J. Opt. Soc. Am. B 5, 1317–1322 (1988) .
Wallraff, A. et al. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 431, 162–167 (2004) .
Koch, J. et al. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A 76, 042319 (2007) .
Wallraff, A. et al. Approaching unit visibility for control of a superconducting qubit with dispersive readout. Phys. Rev. Lett. 95, 060501 (2005) .
Gardiner, C. W. & Zoller, P. . Quantum Noise: A Handbook of Markovian and Non-Markovian Quantum Stochastic Methods with Applications to Quantum Optics Springer-Verlag, Berlin (2004) .
Wódkiewicz, K., Shore, B. W. & Eberly, J. H. . Noise in strong laser-atom interactions: frequency fluctuations and nonexponential correlations. Phys. Rev. A 30, 2390–2398 (1984) .
Mukamel, S., Oppenheim, I. & Ross, J. . Statistical reduction for strongly driven simple quantum systems. Phys. Rev. A 17, 1988–1998 (1978) .
Dykman, M. I., Khasin, M., Portman, J. & Shaw, S. W. . Spectrum of an oscillator with jumping frequency and the interference of partial susceptibilities. Phys. Rev. Lett. 105, 230601 (2010) .
Sagi, Y., Pugatch, R., Almog, I., Davidson, N. & Aizenman, M. . Motional broadening in ensembles with heavy-tail frequency distribution. Phys. Rev. A 83, 043821 (2011) .
Oliver, W. D. et al. Mach-Zehnder interferometry in a strongly driven superconducting qubit. Science 310, 1653–1657 (2005) .
Tuorila, J. et al. Stark effect and generalized Bloch-Siegert shift in a strongly driven two-level system. Phys. Rev. Lett. 105, 257003 (2010) .
Noel, M. W., Griffith, W. M. & Gallagher, T. F. . Frequency-modulated excitation of a two-level atom. Phys. Rev. A 58, 2265–2273 (1998) .
Shevchenko, S. N., Ashhab, S. & Nori, F. . Landau-Zener-Stückelberg interferometry. Phys. Rep. 492, 1–30 (2010) .
Ballester, D., Romero, G., García-Ripoll, J. J., Deppe, F. & Solano, E. . Quantum simulation of the ultrastrong-coupling dynamics in circuit quantum electrodynamics. Phys. Rev. X 2, 021007 (2012) .
Casanova, J., Romero, G., Lizuain, I., García-Ripoll, J. J. & Solano, E. . Deep strong coupling regime of the Jaynes-Cummings model. Phys. Rev. Lett. 105, 263603 (2010) .
Niemczyk, T. et al. Circuit quantum electrodynamics in the ultrastrong-coupling regime. Nat. Phys. 6, 772–776 (2010) .
Forn-Díaz, P. et al. Observation of the Bloch-Siegert shift in a qubit-oscillator system in the ultrastrong coupling regime. Phys. Rev. Lett. 105, 237001 (2010) .
Shnirman, A., Schön, G., Martin, I. & Makhlin, Y. . Low- and high-frequency noise from coherent two-level systems. Phys. Rev. Lett. 94, 127002 (2005) .
Martinis, J. M. et al. Decoherence in Josephson qubits from dielectric loss. Phys. Rev. Lett. 95, 210503 (2005) .
Yoshihara, F., Harrabi, K., Niskanen, A. O., Nakamura, Y. & Tsai, J. S. . Decoherence of flux qubits due to 1/f flux noise. Phys. Rev. Lett. 97, 167001 (2006) .
Beaudoin, F., da Silva, M. P., Dutton, Z. & Blais, A. . First-order sidebands in circuit QED using qubit frequency modulation. Phys. Rev. A 86, 022305 (2012) .
Brickman Soderberg, K.-A. & Monroe C. . Phonon-mediated entanglement for trapped ion quantum computing. Rep. Prog. Phys. 73, 036401 (2010) .
Graham, R. . Squeezing and frequency changes in harmonic oscillations. J. Mod. Opt. 34, 873–879 (1987) .
Houck, A. A., Türeci, H. E. & Koch, J. . On-chip quantum simulation with superconducting circuits. Nat. Phys. 8, 292–298 (2012) .
Friedenauer, A., Schmitz, H., Glueckert, J. T., Porras, D. & Schaetz, T. . Simulating a quantum magnet with trapped ions. Nature Phys. 4, 757–761 (2008) .
Nayak, N. & Agarwal, G. S. . Absorption and fluorescence in frequency-modulated fields under conditions of strong modulation and saturation. Phys. Rev. A 31, 3175–3182 (1985) .
Kador, L., Latychevskaia, T., Renn, A. & Wild, U. P. . Radio-frequency Stark effect modulation of single-molecule lines. J. Lumin. 86, 189–194 (2000) .
Sillanpää, M., Lehtinen, T., Paila, A., Makhlin, Y. & Hakonen P. . Continuous-time monitoring of Landau-Zener interference in a Cooper-pair box. Phys. Rev. Lett. 96, 187002 (2006) .
Acknowledgements
We thank S. Girvin and J. Viljas for discussions. This work was done under the Center of Excellence `Low Temperature Quantum Phenomena and Devices' (project 250280) of the Academy of Finland. G.S.P. acknowledges support from the Academy of Finland, projects 141559, 253094, and 135135. M.P.S. was supported by the Magnus Ehrnrooth Foundation and together with J.-M.P. by the Finnish Academy of Science and Letters (Vilho, Yrjö ja Kalle Väisälä Foundation). J.-M.P. acknowledges also the financial support from Emil Aaltonen Foundation and KAUTE Foundation. The contribution of M.A.S. was done under an ERC Starting Grant. J.L. and M.P.S. acknowledge partial support from NGSMP.
Author information
Authors and Affiliations
Contributions
J.L., K.S.K., and G.S.P. designed and performed the experiment. M.P.S. carried out the theoretical work. A.V., W.C.C., and M.P.S. contributed to experiments. J.-M.P. fabricated the sample. J.T. and E.V.T. provided theoretical support. J.L. and M.P.S. co-wrote the manuscript in co-operation with all the authors. M.A.S., P.J.H., E.V.T. and G.S.P. provided support and supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures S1-S5 and Supplementary Notes S1-S3 (PDF 1014 kb)
Rights and permissions
About this article
Cite this article
Li, J., Silveri, M., Kumar, K. et al. Motional averaging in a superconducting qubit. Nat Commun 4, 1420 (2013). https://doi.org/10.1038/ncomms2383
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms2383
This article is cited by
-
Quantum phase transition of the Jaynes-Cummings model
Science China Physics, Mechanics & Astronomy (2024)
-
Dressed-state control of effective dipolar interaction between strongly-coupled solid-state spins
npj Quantum Information (2023)
-
Frequency–modulated qubits in a dissipative cavity: entanglement dynamics and protection
Quantum Information Processing (2023)
-
Two-time correlation functions beyond quantum regression theorem: effect of external noise
Quantum Information Processing (2021)
-
Simulating Anisotropic quantum Rabi model via frequency modulation
Scientific Reports (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.