Abstract
The study of carrier multiplication has become an essential part of many-body physics and materials science as this multiplication directly affects nonlinear transport phenomena, and has a key role in designing efficient solar cells and electroluminescent emitters and highly sensitive photon detectors. Here we show that a 1-MVcm−1 electric field of a terahertz pulse, unlike a DC bias, can generate a substantial number of electron–hole pairs, forming excitons that emit near-infrared luminescence. The bright luminescence associated with carrier multiplication suggests that carriers coherently driven by a strong electric field can efficiently gain enough kinetic energy to induce a series of impact ionizations that can increase the number of carriers by about three orders of magnitude on the picosecond time scale.
Similar content being viewed by others
Introduction
Impact ionization originates from the Coulomb interaction between carriers and is essentially the reverse of the Auger recombination process1. In this process, a highly energetic conduction-band electron (e11) colliding with a valence-band electron gives two conduction electrons (e12+e22) and a hole (h21). The electron e11 gains energy in the strong electric field, and this energy gain implies that carriers driven without being affected by incoherent phonon scattering efficiently acquire enough kinetic energy to trigger a series of impact ionizations, that is, carrier multiplication2,3. This multiplication process has an important role in the efficient working of photovoltaic nanomaterials4,5,6,7, electroluminescent emitters8,9 and highly sensitive photon detectors used in optical quantum information applications10. However, despite the fact that carrier-initiated impact ionization in a strong electric field critically affects non-equilibrium quantum transport phenomena11,12,13,14, the elementary process of carrier scattering relevant to ballistic transport has yet to be clarified.
Intense terahertz (THz) pulse sources have the potential to provide significant insights into ultra-fast carrier multiplication through purely optical methods, because a THz pulse has a high electric-field amplitude (>0.1 MVcm−1) and lasts a picosecond15,16,17. It has been shown that electrons in the conduction band of GaAs undergo ballistic motion without incoherent longitudinal optical (LO) phonon scattering for periods on time scales of hundreds of femtoseconds (2π ωLO− 1=115 fs, where ωLO is the angular frequency of the LO phonon)18. Carriers accelerated ballistically on ultra-short time scales can therefore be expected to gain kinetic energy more efficiently and thereby trigger carrier multiplication. However, insufficiently strong THz pulses generate few carriers19, and various additional phenomena observed by THz and optical absorption measurements—such as phonon absorption20, intervalley scattering21 and exciton dissociations22,23—obscure the carrier multiplication.
In this article, we highlight the extraordinarily efficient carrier multiplication in the typical semiconductor GaAs when it is subjected to a THz pulse of a strong electric field. We demonstrate for the first time that the electric field of a THz pulse, unlike a DC bias, can generate a substantial number of excitons that emit near-infrared luminescence without any help from band-to-band photoexcitation. Our results imply that the carriers coherently driven by a strong electric field can efficiently gain enough kinetic energy to induce a series of impact ionizations that can increase the number of carriers by about three orders of magnitude on the picosecond time scale.
Results
Carrier multiplication with THz pulse excitation
We developed an experimental scheme for studying carrier multiplication in nominally undoped GaAs quantum wells (QWs) with intense THz pulses (Fig. 1a, Methods). Carrier multiplication was induced by irradiating the QW sample with a nearly half-cycle THz pulse lasting 1 ps and having a maximum peak electric field amplitude of 1.05 MVcm−1 (Methods)24. The THz pulses were focused onto a GaAs QW sample that was mounted on the cold finger of a helium-flow cryostat. The electric field polarization was perpendicular to the stacking direction and along the (100) direction of the sample. As the thickness of the QWs (L=6 μm) is sufficiently thin compared with the centre wavelength of THz pulse (~300 μm; Fig. 1b), the constructive interference inside the sample modifies the strength and shape of the incident THz pulse (Methods).
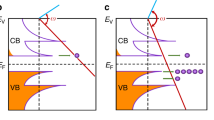
(a) Generated THz pulses are focused onto the GaAs QWs sample, and the luminescence is detected by a CCD camera after it has passed through a spectrometer. (b) The geometry of the sample interfaces with air (nA=1), QWs (nQW=3.5) and a quartz substrate (nS=2.1). We assume here that the QWs with thickness (L=6 μm) on the quartz substrate has a homogeneous refractive index (nQW=3.5) represented by the average of the refractive indices of the wells (nw=3.6) and barriers (nb=3.4). ɛi(t, x) is incident THz electric field from the air. (c) Electron-initiated impact ionization transitions in the schematic GaAs band structure for momentum in the Δ direction. The lattice constant a of GaAs is 5.6 Å, and ±2π/a corresponds to ±1.1×1010 m−1. The diagram shows electrons and hole positions before and after the transition at the threshold.
The field ionization due to the THz pulse caused electrons from residual impurity donors to be accelerated along the Δ line around the Brillouin zone centre (Γ point) in momentum space as shown in Figure 1c (see the Methods section for a description of the field ionization)25. When the electric field reached a certain strength, the electrons acquired enough energy to induce several impact ionizations and produce substantial numbers of electron–hole (e–h) pairs that go on to form excitons around the Γ point. The impulsive electric field of the pulse allowed the unbound e–h pairs to form excitons that decayed radiatively because the electric field that would otherwise ionize the exciton was absent just after the pairs were generated22,23,26. The luminescence from the excitons was detected by a liquid-nitrogen-cooled charge-coupled device (CCD) camera (Fig. 1a).
Excitation intensity dependence
Figure 2a clearly shows that THz pulses with different field strengths induce near-infrared luminescence centred around 1.55 eV from QWs at 10 K, even though the central photon energy of the pulse (~4 meV) is about 390 times lower than the luminescence photon energy24, and the luminescence intensity drastically decreases as the electric field ɛ decreases. As luminescence is proportional to the created e–h pair density27, the generated carrier density N can be estimated by comparing the luminescence measurement with optical pulse excitation measurements (Methods). As shown in Figure 2b, the carrier density N plotted as a function of THz pulse fluence I is extremely nonlinear and roughly proportional to I4 ( ɛ8). The minimum and maximum fluences correspond to electric fields of 0.47 and 1.05 MVcm−1, and the carrier density increases over this range by about three orders of magnitude. Moreover, the shape of the emission spectra does not have any field dependence (inset of Fig. 2a), which suggests that high-density excitation phenomena do not occur at these excitation intensity energies28.
ɛ8). The minimum and maximum fluences correspond to electric fields of 0.47 and 1.05 MVcm−1, and the carrier density increases over this range by about three orders of magnitude. Moreover, the shape of the emission spectra does not have any field dependence (inset of Fig. 2a), which suggests that high-density excitation phenomena do not occur at these excitation intensity energies28.
(a) Spectra of luminescence excited at 10 K by THz pulses with peak electric field amplitudes of 0.54 MVcm−1 (green dotted line), 0.70 MVcm−1 (blue dashed line) and 1.05 MVcm−1 (red solid line). Inset: normalized luminescence spectrum excited with the different electric field strengths. (b) THz pulse excitation intensity dependence of peak luminescence intensity (magenta closed circles). The eye guide (black solid line) corresponds to a fourth-power-law intensity dependence.
Origin of luminescence
We attempted to identify the origin of the observed luminescence by comparing the luminescences induced by a 1.05 MVcm−1 THz pulse and by a 3.18-eV optical pulse. As shown in Figure 3a, the spectral shapes are almost the same, and the peak photon energies are near the heavy-hole (hh) exciton absorption peak. The luminescence induced by the THz pulse can therefore be inferred to be from radiative recombination of hh excitons. Figure 3b shows the temperature dependence of peak luminescence intensities obtained from the THz and optical pulse excitations. The temperature dependences are very similar, suggesting that these two kinds of pulses induce similar non-radiative decay processes of e–h pairs that contribute in almost the same way to their recombination processes. The ratio plotted in the inset of Figure 3b shows almost no temperature dependence, and this means that the exciton generation processes driven by THz pulses and optical pulses have similar temperature dependences. In contrast to the similar temperature dependences, the extremely nonlinear enhancement of luminescence intensity as a function of THz field strength nevertheless indicates that the e–h pair creation mechanism due to THz-pulse irradiation is completely different from the one due to photoexcitation.
(a) Spectra of luminescence at 10 K excited by a 1.05 MVcm−1 THz pulse (red solid line) and optical pulse with centre photon energy of 3.18 eV (grey open circles) (fluence absorbed by the sample is ~6 μJcm−2). (b) Temperature dependence of peak luminescence intensities excited by THz (red closed circles) and optical pulses (blue open circles). Inset: temperature dependence of intensity ratios as calculated by dividing the peak luminescence intensity due to a THz pulse by that due to the optical pulse (purple open circles).
Discussion
We attribute the generation of substantial numbers of carriers to highly efficient carrier multiplication triggered by impact ionizations rather than to Zener tunnelling. Note that we can exclude Zener tunnelling as a cause because the tunnelling occurring under a 1 MVcm−1 DC electric field lasting 1 ps can account for only a small amount of the e–h pairs (1011 cm−3)29, far too small to explain the observation (Fig. 2b). In the impact ionization process1, an electron in the conduction band (e11), with kinetic energy gained from the electric field, creates an electron (e12) plus an e–h pair (e22+h21) (Fig. 1c):

In accordance with energy and momentum conservation, this process is possible only if the electron has a threshold kinetic energy Eth higher than the band gap Eg of 1.52 eV. Here, Eth=Eg (2me+mhh)/(me+mhh)=1.7 eV30, where me (=0.067 m0) and mhh (=0.5 m0) are the effective masses of the electron and heavy hole, respectively. As shown in the sketch of Figure 4a, if an electron released from an impurity donor can be accelerated to the threshold kinetic energy, it can create an e–h pair (Fig. 1c). Subsequently, both the electron that lost energy to create the e–h pair and the created e–h pair could, in turn, gain energy from the field. This process can continue as long as the electric field of the THz pulse remains sufficiently strong, and so, comparably few impact ionization events can nevertheless produce numerous e–h pairs.
(a) The sketch visualizes the distortion in the Coulomb potential of donors, causing the potential to widen and free electrons to be released, and subsequent evolution of unbound e-h gas generated by a series of impact ionizations into a pure population of excitons emitting luminescence. (b) Electric field dependences of carrier density obtained in the experiment (red open circle) and calculations using equation (2) for three different impact ionization rates γ Ical; one is infinity (grey solid line), and the others are derived from equation (3) with C=C0=870 ps−1 eV−2 (green one-dot-dashed line) and C=5C0 (blue two-dot-dashed line). We assumed N0=1013 cm−3. For the experimental (red open circles) and calculated data (grey solid line), the carrier density N is plotted together with the corresponding 〈nI〉. Panels (c) and (d) show the electron wavenumber k(t) calculated by using equation (2) for ɛ=1.05 and 0.47 MVcm−1, respectively. Dashed lines indicate the wavenumbers in the range of ±2.77×109 m−1, where the electron energy corresponds to the threshold energy Eth of 1.7 eV determined from the dispersion of the GaAs band structure. (e) Normalized electric field of the temporal profile of the incident THz pulse (grey dotted line) and of THz pulse with multiple reflections inside the sample (orange solid line).
This intuitive consideration of the multiplication dynamics leads to a prediction that can be compared with experimental observation. As can be seen in equation (1), an electron-initiated impact ionization event doubles the number of electrons. That is, given an initial electron density N0, the electron and hole densities after 〈nI〉 impact ionization events are, respectively, and N0× . We can neglect the contribution of the generated heavy holes because their large effective mass would increase the threshold energy Eth to 2.9 eV. Thus, the increase in impact ionizations 〈ΔnI〉 that is due to changing the electric field from ɛmin=0.47 to ɛmax=1.05 MVcm−1 can be evaluated from the results to be log2(N(ɛmax)/N(ɛmin))~9 (red open circles in Fig. 4b). That is, at least nine impact ionizations on average occur within the 1-ps duration of the THz pulse. Hence, the impact ionization rate γI for the maximum peak electric field is ~9/1×10−12 s–1013 s−1.
The experimentally obtained impact ionization rate γI can be quantitatively compared with a simple theoretical prediction, whereby the motion of an electron in an electric field follows the dispersion of the band structure in momentum space. Here, we take the number of impact ionization events 〈nI(ɛ)〉 to be the number of times the average kinetic energy of the electrons reaches the Eth of 1.7 eV; the GaAs dispersion relation provides this Eth at a wavenumber k of ±2.77×109 m−1 (ref. 25). The change in electron wavenumber k(t) is solely determined by the electric field ɛ (t) acting on the electrons, because of the negligible influence of phonon scattering processes during periods of hundreds of femtoseconds19:

where e is the electron charge and  is Planck's constant. Here, we used the electric field of a THz pulse with multiple reflections inside the sample (Methods). The change in electron wavenumber k(t) during the THz pulse is calculated under the assumption that the electrons lose all their kinetic energy when they reach the average wavenumber ±2.77×109 m−1, that is, an infinite impact ionization rate γ Ical of electrons (Fig. 4c–e).
is Planck's constant. Here, we used the electric field of a THz pulse with multiple reflections inside the sample (Methods). The change in electron wavenumber k(t) during the THz pulse is calculated under the assumption that the electrons lose all their kinetic energy when they reach the average wavenumber ±2.77×109 m−1, that is, an infinite impact ionization rate γ Ical of electrons (Fig. 4c–e).
Accordingly, the e-h densities N(ɛ) after the 〈nI(ɛ)〉 impact ionization events can be estimated to be N0× (grey solid line in Fig. 4b). The theoretical increase in number 〈ΔnI〉 from ɛmin=0.47 to ɛmax=1.05 MVcm−1 is 〈nI(ɛmax) 〉−〈 nI(ɛmin)〉=12, and this estimate would also be subject to an uncertainty of around ±30%, owing mainly to the error in measuring the strength of the THz electric field. Hence, we can say it is close to the experimentally obtained 〈ΔnI〉, and it confirms the validity of the experimentally derived γI of ~1013 s−1. This high-impact ionization rate means that there are too few phonon interactions to prevent carriers from being driven coherently and multiplied efficiently during intervals of hundreds of femtoseconds. This conclusion is consistent with the temperature independence of the luminescence intensity ratio (see the inset of Fig. 3b). If phonon scattering were a significant process on the sub-picosecond time scale, the efficiency of carrier generation due to THz pulse irradiation would be lower and the ratio would decrease with increasing temperature and phonon population. The assumption of an infinite γ Ical is reasonable only if the impact ionization time τI=(γ Ical)−1 is sufficiently short compared with the time τa for the electron energy to reach Eth from zero. The similar values of 〈ΔnI〉 between the experiment (~9 times) and calculation (~12 times) suggest that τI is sufficiently shorter than τa. If the values were otherwise, the experimentally derived 〈nI〉 would be suppressed and the carrier multiplication could not occur so as to induce a 1000-fold increase in carrier density.
We also theoretically analysed the observed carrier density with a finite impact ionization rate γ Ical, which is modelled according to the well-established Keldysh formula32:

The corresponding values for electrons are taken from Fischetti and Laux31: C=C0=870 ps−1 eV−2 and Eth=1.7 eV. As shown in Figure 4b, when we use a value of C=5C0 in equation (3), the calculation (blue two-dot-dashed line) reproduces the experimentally observed carrier density and is close to the curve calculated under the assumption of infinite γ Ical (grey solid line). Here, γ Ical=2.5×1014 s−1 can be derived by using equation (3) with C=5C0 and E=1.94 eV at the maximum first-conduction-band energy between Γ and X points. The value γI (~1013 s−1) obtained experimentally is almost ten times smaller than the calculated γ Ical. The finite time for electrons to accelerate to Eth can be the reason for the lower experimental value.
The observed saturation behaviour at stronger electric fields in Figure 4b can be qualitatively understood to be from an enhancement in Coulomb scattering among the generated carriers. Figure 5 plots the carrier density in the QWs sample as a function of time, which can be calculated by using N0× and the time development of impact ionization events 〈nI〉 during the THz pulse (Fig. 4c–e). Under strong electric fields, the substantial numbers of e–h pairs generated at the earlier stage of multiplication may undergo a significant amount of e–h scattering. The scattering decelerates the electrons and reduces their ability to gain kinetic energy. Moreover, e-e scattering could lead to a redistribution of energy within the electron system, which may in turn reduce the average kinetic energy of a given carrier below the threshold and suppress the impact ionization events. Eventually, unbound e–h pairs generated with an energy conversion efficiency of ~5×10−4 (Methods) may form excitons that have a relaxation time τPL of several nanoseconds (τPL as determined by the radiative and non-radiative relaxation times; see Fig. 4a).
(a) Calculated carrier density N(t) as a function of time for different electric field strengths, which can be calculated by using N0× and the time development of impact ionization events 〈nI〉 during the THz pulse; 0.47 MVcm−1 (blue solid line), 0.70 MVcm−1 (green solid line) and 1.05 MVcm−1 (red solid line).
In conclusion, we demonstrated extraordinarily high carrier multiplication in the typical semiconductor GaAs when it is subjected to a THz pulse of a strong electric field; the number of carriers increased by about three orders of magnitude. The carrier multiplication increase that occurs with an increase in the THz electric field was in agreement with phenomenological theory based on an impact ionization model including electron motion in k-space with a pristine band structure. In the future, a full quantum kinetic theory treatment of carrier dynamics in a band structure modified by an intense THz electric field should be performed to reveal the microscopic origin of the carrier multiplication32. Moreover, an experiment with a time-delayed probe pulse would allow for the carrier multiplication dynamics to be directly probed. Our findings of efficient ultra-fast carrier multiplication bode well for future applications in ultra-high-speed devices such as high-quantum-efficiency THz-biased avalanche photodiodes that have femtosecond resolution and are sensitive to a single photon, and they may also be exploited in the development of efficient electroluminescent and photovoltaic nanoscale devices.
Methods
Samples
A sample of nominally undoped GaAs/Al0.3Ga0.7As QWs was grown by molecular beam epitaxy on a (100)-GaAs substrate. It consisted of 272 periods of GaAs QWs (11.9 nm) separated from each other by Al0.3Ga0.7As barriers (10 nm). We removed the GaAs substrate by wet etching and placed the QWs film on a Z-cut quartz substrate (Fig. 1b). The dominant donor impurities were sulphur from an arsenide source. The static electric field ɛion necessary to ionize the sulphur donor is estimated as ɛion=Eb/eaB~4 kVcm−1, where e is the charge of the electron and Eb and aB are the binding energy and Bohr radius of the impurity donor in bulk GaAs, respectively. The Eb given by the literature is ~6 meV, and aB (=ɛ0a0m0/m*) is estimated to be ~10 nm, where ɛ0=12.4 and m*=0.067 m0 are the dielectric constant and effective mass of an electron in bulk GaAs, respectively, and a0 is the Bohr radius in the hydrogen atom33. This ionizing field is much lower than the minimum peak field of 0.47 MVcm−1 to see the luminescence. Consequently with this set up, the donors are completely ionized during the rise time of each THz pulse, and the released electrons trigger the carrier multiplication process (Fig. 4a).
Measurements
High-electric-field THz pulses were generated by optical rectification of femtosecond laser pulses in LiNbO3 by using the tilted-pump-pulse-front scheme15,16,17,24. For the pump source, we used an amplified Ti:sapphire laser that provided a pulse energy of 4 mJ, a full width at half-maximum intensity of 85 fs, a central wavelength of 780 nm and a repetition rate of 1 kHz. The optical pulses from the oscillator with a repetition rate of 80 MHz synchronized with the amplified pulses were used for electro-optic sampling of THz pulses at the sample position24. The THz pulse energy measured by a pyroelectric detector (MicroTech Instruments, Inc.) was 2.3 μJ at an electric field of 1.05 MVcm−1. The generated luminescence was analysed with a spectrometer with a resolution of about 1 meV and detected by a liquid-nitrogen-cooled CCD camera. To prevent stray near-infrared pulse laser light from entering the CCD camera, we put a black polypropylene sheet whose Fresnel coefficient for transmission in the THz frequency region was 0.87 in front of the cryostat window. To change the THz pump fluence, we put black polypropylene sheets in the THz-beam path.
Electric field of the THz pulse inside the sample
Figure 1b shows the geometry of the sample interfaces with air (nA=1) and the quartz substrate (nS=2.1). We assume here that the QWs has a homogeneous refractive index nQW that is the average of the refractive indices of the wells (nw=3.6) and barriers (nb=3.4), that is, 3.5. The electric field ɛ (t, x) inside the QWs in which multiple reflections take place can be written as follows:

where ɛi(t, x) is incident THz electric field from the air, N is the number of round trips, c is the speed of light, [ttilde]=2/(nQW+1) is the Fresnel transmittance between the air and sample, [ttilde]1=(nQW−1)/(nQW+1) is the Fresnel reflectance at the air and sample interface, [ttilde]2=(nQW−nS)/(nQW+nS) is the Fresnel reflectance at the sample and substrate interface and τ0=nQW L/c is the phase shift. L is the thickness of the QWs. Consequently, the ratio of the maximum values of the positive lobe between the 6-μm thick and an infinitely thick QWs increases to 1.2. The maximum peak electric field inside the sample is estimated to be 0.55 MVcm−1 in the case of a 1.05 MVcm−1 electric field incidence.
Estimation of carrier density
The carrier density N generated by a 1.05 MVcm−1 THz pulse can be estimated by the following equation,

where CTHz is the total number of carriers and dw (=3.2 μm) is the length of the sample's GaAs wells alone (excluding the AlGaAs barriers). The effective diameter of the excited spot area aeff (~100 μm) is obtained by dividing the spot diameter in the electric field ain (~300 μm) by a factor of  , as the generated carrier density roughly follows an 8th power law of the incident electric field (Fig. 2b). We obtained the same PL intensity with a THz pulse with a peak field value of ɛmax as with an optical pulse with a photon energy p of 3.18 eV, a spot diameter aopt of ~100 μm and absorbed fluence F of 6 μJcm−2. The carrier numbers were about the same because the spot diameters of aeff and aopt were almost the same value (~100 μm). Accordingly,
, as the generated carrier density roughly follows an 8th power law of the incident electric field (Fig. 2b). We obtained the same PL intensity with a THz pulse with a peak field value of ɛmax as with an optical pulse with a photon energy p of 3.18 eV, a spot diameter aopt of ~100 μm and absorbed fluence F of 6 μJcm−2. The carrier numbers were about the same because the spot diameters of aeff and aopt were almost the same value (~100 μm). Accordingly,  , where e=1.6×10−19 eV−1J. (The uncertainties of the carrier densities N are typically ±50%, owing mainly to the errors in the measurement of the optical excitation fluence and spot diameter of the THz pulse.)
, where e=1.6×10−19 eV−1J. (The uncertainties of the carrier densities N are typically ±50%, owing mainly to the errors in the measurement of the optical excitation fluence and spot diameter of the THz pulse.)
Energy conversion efficiency
The energy conversion efficiency Q from the THz pulse energy WINTHz absorbed in the sample with respect to the impact ionization process Wii can be estimated from the generated carrier density. Part of the absorbed energy of the incident THz pulse goes into the impact ionization process; the other parts go into free carrier absorption and the transmitted THz pulse. The efficiency Q is defined as

where Eth=1.7 eV is the threshold energy of impact ionization. As the absorbed THz pulse energy WINTHz is almost 1 μJ, the conversion energy efficiency Q is estimated to be ~5×10−4.
Additional information
H.H. conducted the experiments and wrote the paper. H.H. and K.S. performed the measurements and analysed the data. H.H., K.S., M.S. and S.T. modelled the data. Y.K. designed and fabricated the sample. H.H. and K.T. initiated and provided management oversight for this project. All authors contributed to discussions and the final manuscript.
Additional information
How to cite this article: Hirori, H. et al. Extraordinary carrier multiplication gated by a picosecond electric field pulse. Nat. Commun. 2:594 doi: 10.1038/ncomms1598 (2011).
References
Ferry, D. K. Semiconductor Transport, Taylor & Francis, 2000.
Wolff, P. A. Theory of electron multiplication in silicon and germanium. Phys. Rev. 95, 1415–1420 (1954).
Shockley, W. Problems related to p-n junctions in silicon. Solid-State Electron. 2, 35–67 (1961).
Schaller, R. D. & Klimov, V. I. High efficiency carrier multiplication in PbSe nanocrystals: implications for solar energy conversion. Phys. Rev. Lett. 92, 186601 (2004).
Tian, B. et al. Coaxial silicon nanowires as solar cells and nanoelectronic power sources. Nature 449, 885–889 (2007).
Gabor, N. M., Zhong, Z., Bosnick, K., Park, J. & McEuen, P. L. Extremely efficient multiple electron-hole pair generation in carbon nanotube photodiodes. Science 325, 1367–1371 (2009).
Pijpers, J. J. et al. Assessment of carrier-multiplication efficiency in bulk PbSe and PbS. Nat. Phys. 5, 811–814 (2009).
Misewich, J. A., Martel, R., Avouris, P., Tsang, J. C., Heinze, S. & Tersoff, J. Electrically induced optical emission from a carbon nanotube FET. Science 300, 783–786 (2003).
Chen, J. et al. Bright infrared emission from electrically induced excitons in carbon nanotubes. Science 310, 1171–1174 (2005).
Hadfield, R. H. Single-photon detectors for optical quantum information applications. Nat. Photon. 3, 696–705 (2009).
Haug, H. & Jauho, A.- P. Quantum Kinetics in Transport and Optics of Semiconductors, Springer, 1996.
Dekorsy, T., Pfeifer, T., Kütt, W. & Kurz, H. Subpicosecond carrier transport in GaAs surface-space-charge fields. Phys. Rev. B 47, 3842–3849 (1993).
Hu, B. B. et al. Identifying the distinct phases of carrier transport in semiconductors with 10 fs resolution. Phys. Rev. Lett. 74, 1689–1692 (1995).
Leitenstorfer, A., Hunsche, S., Shah, J., Nuss, M. C. & Knox, W. H. Femtosecond high-field transport in compound semiconductors. Phys. Rev. B 61, 16642–16652 (2000).
Gaal, P. et al. Internal motions of a quasiparticle governing its ultrafast nonlinear response. Nature 450, 1210–1213 (2007).
Hebling, J., Almási, G., Kozma, I. Z. & Kuhl, J. Velocity matching by pulse front tilting for large area THz-pulse generation. Opt. Express 10, 1161–1166 (2002).
Yeh, K.- L., Hoffmann, M. C., Hebling, J. & Nelson, K. A. Generation of 10 μJ ultrashort terahertz pulses by optical rectification. Appl. Phys. Lett. 90, 171121 (2007).
Hoffmann, M. C. & Fülöp, J. A. Intense ultrashort terahertz pulses: generation and applications. J. Phys. D: Appl. Phys. 44, 08301–08317 (2011).
Kuehn, W., Gaal, P., Reimann, K., Woerner, M., Elsaesser, T. & Hey, R. Coherent ballistic motion of electrons in a periodic potential. Phys. Rev. Lett. 104, 146602 (2010).
Wen, H., Wiczer, M. & Lindenberg, A. M. Ultrafast electron cascades in semiconductors driven by intense femtosecond terahertz pulses. Phys. Rev. B 78, 125203 (2008).
Hoffmann, M. C., Hebling, J., Hwang, H. Y., Yeh, K.- L. & Nelson, K. A. Impact ionization in InSb probed by terahertz pump-terahertz probe spectroscopy. Phys. Rev. B 79, 161201 (R) (2009).
Hebling, J., Hoffmann, M. C., Hwang, H. Y., Yeh, K.- L. & Nelson, K. A. Observation of nonequilibrium carrier distribution in Ge, Si, and GaAs by terahertz pump-terahertz probe measurements. Phys. Rev. B 81, 035201 (R) (2010).
Hirori, H., Nagai, M. & Tanaka, K. Excitonic interactions with intense terahertz pulses in ZnSe/ZnMgSSe multiple quantum wells. Phys. Rev. B 81, 081305 (R) (2010).
Watanabe, S., Minami, N. & Shimano, R. Intense terahertz pulse induced exciton generation in carbon nanotubes. Opt. Express 19, 1528–1538 (2011).
Hirori, H., Doi, A., Blanchard, F. & Tanaka, K. Single-cycle terahertz pulses with amplitudes exceeding 1 MVcm−1 generated by optical rectification in LiNbO3 . Appl. Phys. Lett. 98, 091106 (2011).
Cohen, M. L. & Bergstresser, T. K. Band Structures and pseudopotential form factors for fourteen semiconductors of the diamond and zinc-blende structures. Phys. Rev. 141, 789–796 (1966).
Miller, D. A. B. et al. Electric field dependence of optical absorption near the band gap of quantum-well structures. Phys. Rev. B 32, 1043–1060 (1985).
Kaindl, R. A., Hägele, D., Carnahan, M. A. & Chemla, D. S. Transient terahertz spectroscopy of excitons and unbound carriers in quasi-two-dimensional electron-hole gases. Phys. Rev. B 79, 045320 (2009).
Tränkle, G., Leier, H., Forchel, A., Haug, H., Ell, C. & Weimann, G. Dimensionality dependence of the band-gap renormalization in two- and three-dimensional electron-hole plasmas in GaAs. Phys. Rev. Lett. 58, 419–422 (1987).
Kane, E. O. Zener tunneling in semiconductors. J. Phys. Chem. Solids 12, 181–188 (1960).
Anderson, C. L. & Crowell, C. R. Threshold energies for electron-hole pair production by impact ionization in semiconductors. Phys. Rev. B 5, 2267–2272 (1972).
Fischetti, M. V. & Laux, S. E. Monte Carlo analysis of electron transport in small semiconductor devices including band-structure and space-charge effects. Phys. Rev. B 38, 9721–9745 (1988).
Blanchard, F. et al. Effective mass anisotropy of hot electrons in nonparabolic conduction bands of n-doped InGaAs films using ultrafast terahertz pump-probe techniques. Phys. Rev. Lett. 107, 107401 (2011).
Yu, P. Y. & Cardona, M. Fundamentals of Semiconductors: Physics and Materials Properties, Springer, 2001.
Acknowledgements
H.H. is grateful to Takao Aoki, Atsushi Doi and François Blanchard for encouraging discussions and also wishes to acknowledge Grant-in-Aid for Young Scientists (B) (Grant No. 21760038) of Japan Society for the Promotion of Science. We are thankful to Yousuke Kayanuma and Kenichi Ishikawa for discussions. This work was supported by Grant-in-Aid for Scientific Research on Innovative Area 'Optical science of dynamically correlated electrons (DYCE)' (Grant No. 20104007) and Grant-in-Aid for Creative Scientific Research (Grant No. 18GS0208) of the Ministry of Education, Culture, Sports, Science and Technology, Japan.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-Share Alike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Hirori, H., Shinokita, K., Shirai, M. et al. Extraordinary carrier multiplication gated by a picosecond electric field pulse. Nat Commun 2, 594 (2011). https://doi.org/10.1038/ncomms1598
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms1598
This article is cited by
-
Terahertz radiation by quantum interference of excitons in a one-dimensional Mott insulator
Nature Communications (2023)
-
Ultrafast imaging of terahertz electric waveforms using quantum dots
Light: Science & Applications (2022)
-
Terahertz strong-field physics in light-emitting diodes for terahertz detection and imaging
Communications Physics (2021)
-
Impact ionization and intervalley electron scattering in InSb and InAs induced by a single terahertz pulse
Scientific Reports (2020)
-
Impact Ionization Induced by Terahertz Radiation in HgTe Quantum Wells of Critical Thickness
Journal of Infrared, Millimeter, and Terahertz Waves (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.