Abstract
The first known magnetic mineral, magnetite, has unusual properties, which have fascinated mankind for centuries; it undergoes the Verwey transition around 120 K with an abrupt change in structure and electrical conductivity. The mechanism of the Verwey transition, however, remains contentious. Here we use resonant inelastic X-ray scattering over a wide temperature range across the Verwey transition to identify and separate out the magnetic excitations derived from nominal Fe2+ and Fe3+ states. Comparison of the experimental results with crystal-field multiplet calculations shows that the spin–orbital dd excitons of the Fe2+ sites arise from a tetragonal Jahn-Teller active polaronic distortion of the Fe2+O6 octahedra. These low-energy excitations, which get weakened for temperatures above 350 K but persist at least up to 550 K, are distinct from optical excitations and are best explained as magnetic polarons.
Similar content being viewed by others
Introduction
Since its first X-ray structural elucidation by Bragg1 a hundred years ago and the discovery of the Verwey transition2,3, magnetite (Fe3O4), has received much attention for decades. Even today, it attracts significant scientific and technological interest for its applications in ultrafast magnetic sensors4, palaeomagnetism5, nanomedicine carriers6, and so on. Fe3O4 becomes ferrimagnetic below Tc∼850 K, followed by an abrupt decrease in its electrical conductivity by two orders of magnitude as the temperature is cooled below TV. In this first known magnet to mankind, one-third of Fe sites, termed A-sites, are tetrahedrally (Td) coordinated with oxygens; the other two-thirds, termed B-sites, have octahedral (Oh) coordination. Verwey first suggested a Fe2+–Fe3+ charge-ordering occurring on the B-sites as the driving force of this transition. There are two major schools of interpretation: the first one interprets the Verwey transition as a transition driven by charge/orbital ordering7,8,9,10,11,12,13,14,15,16,17. The second one exploits the mechanism of a lattice distortion-driven electron–phonon coupling18,19,20,21,22 enhanced by the on-site Coulomb interaction and thus opens a gap at the Fermi energy when the temperature is lowered below the Verwey transition temperature TV.
Although numerous investigations have been carried out to verify the charge localization on the B-sites, the charge-ordering pattern of magnetite is subtle and still elusive19,20. While it is agreed that the charge disproportionation involves changes in the nominal Fe2+ and Fe3+ states associated with the B-sites, X-ray diffraction studies of the low-temperature phase of magnetite microcrystals15,17 revealed that the t2g electrons of the B-sites are not fully localized in the form of Fe2+ states. Instead, the electrons are distributed over linear three-Fe-site units termed trimerons, which are coupled to the Td Jahn-Teller distortion of B-site Fe2+O6 octahedra, as illustrated in Fig. 1. To the first approximation, the B-site Fe3+O6 octahedra are Jahn-Teller-inactive. The tetragonal distortion of B-site Fe2+O6 octahedra removes the degeneracy of t2g orbitals, in going from Oh symmetry to D4h symmetry. In the absence of spin–orbit coupling, an effective energy separation  between dxy and dyz/dzx is created if the four Fe–O bonds in the xy plane are elongated or contracted. The trimeron scenario then indicates that the Verwey transition is essentially due to an ordering of trimerons. Because previous results of optical conductivity23 and photoemission24,25,26,27 showed the pseudogap feature of magnetite above TV, and results of entropy analysis28, neutron/X-ray diffuse scattering29 and anomalous phonon broadening22 revealed the short-range order above TV, one important open question is whether trimeron correlations persist in the cubic phase at temperatures above TV. Combining these short-range correlations of polaronic characters with the spin degrees of freedom of t2g electrons, one can expect magnetic polarons in magnetite.
between dxy and dyz/dzx is created if the four Fe–O bonds in the xy plane are elongated or contracted. The trimeron scenario then indicates that the Verwey transition is essentially due to an ordering of trimerons. Because previous results of optical conductivity23 and photoemission24,25,26,27 showed the pseudogap feature of magnetite above TV, and results of entropy analysis28, neutron/X-ray diffuse scattering29 and anomalous phonon broadening22 revealed the short-range order above TV, one important open question is whether trimeron correlations persist in the cubic phase at temperatures above TV. Combining these short-range correlations of polaronic characters with the spin degrees of freedom of t2g electrons, one can expect magnetic polarons in magnetite.
Here we present measurements of resonant inelastic X-ray scattering (RIXS)30,31 at the Fe L3-edge on magnetite to reveal the low-energy spin–orbital excitations of Fe2+ ions in both the monoclinic and cubic phases. To the best of our knowledge, the magnetic excitations derived from the local tetragonal distortion field of Fe2+ ions, that is, magnetic polarons, have not been reported to date. In combination with crystal-field multiplet calculations, we show the the existence of magnetic polarons in magnetite which is driven by the Jahn-Teller distortion.
Results
Fe L3-edge RIXS
Figure 2a shows the Fe L-edge X-ray absorption spectrum of magnetite. By comparing with crystal-field multiplet calculations (see Supplementary Fig. 1), it is understood that the absorption-energy centroid of Fe2+ ions is lower than that of Fe3+ ions by ∼1–2 eV, consistent with earlier work32,33,34. Accordingly, the features at X-ray energies of 706.0 and 707.5 eV originate from the absorption of octahedrally coordinated B-site Fe2+ states, while the maximum intensity feature at 708.8 eV is dominated by absorption from the the Fe3+ ions of both the B-site octahedral and A-site tetrahedral symmetries.
(a) Fe L-edge X-ray absorption spectrum (XAS) spectrum measured in the fluorescence yield mode through the summation of all inelastic X-ray intensities taken at room temperature T=300 K. The XAS is plotted with correction for self-absorption. The incident X-ray energy resolution was 0.5 eV. (b) Colour map of RIXS intensity after correction for self-absorption in the plane of incident photon energy versus energy loss recorded at T=80 K. (c–e) RIXS spectra plotted in terms of energy loss with a vertical offset for clarity. They were recorded by using π-polarized incident X-rays under the scattering geometry of the scattering angle φ=90° and the incident angle φ=20°. Panels c,d were measured at 80 K and e was measured at 550 K.
The colour map of RIXS intensity measured at 80 K in the plane of incident photon energy versus energy loss shown in Fig. 2b presents the evolution of the RIXS spectral profile associated with Fe2+ and Fe3+ ions as detailed in the following. When the incident X-ray energy was set to below 707.5 eV, we observed dd excitations of Fe2+ with energy losses at 2.8±0.05, 1.65±0.05 and 1.16±0.05 eV shown in Fig. 2c, and also a broad excitation centred at 200 meV shown in Fig. 2d. If the incident X-ray energy goes beyond 707.5 eV, the 1.16-eV dd excitation of Fe2+ begins to evolve into a fluorescence that has a constant X-ray emission energy independent of incident energy. With the incident X-ray energy set to 708.8 eV, RIXS excitations arise mostly from Fe3+ ions of octahedral or tetrahedral symmetry.
Figure 2d shows two RIXS features centred at 90 and 200 meV in a magnified plot of energy loss below 0.7 eV. Measurements carried out by varying the scattering angle suggested that these two low-energy excitations do not disperse in momentum space (see Supplementary Fig. 2). The 200-meV excitation has a full-width at half-maximum larger than the instrumental energy resolution. This broad RIXS feature resonates near the L3-edge of Fe2+ and almost disappears for incident energy above 708 eV, at which the other excitation centred at 90 meV emerges. The 90-meV excitation has a full-width at half-maximum nearly equal to the instrumental energy resolution and resonates at 708.4 eV. The distinct incident X-ray energies for these resonant excitations indicate that the 200- and 90-meV features arise from Fe2+ and Fe3+ states, respectively.
Many experimental35,36,37 and theoretical30,38,39,40,41 studies have shown that L-edge RIXS allows spin–flip processes that are not accessible with optical spectroscopy23. For example, if both the incident and scattered X-rays are π-polarized, the spin–flip excitation of dyz is allowed owing to the spin–orbit coupling in the 2p core state. In the present RIXS measurements with a 90°-scattering geometry (see Supplementary Fig. 2a), the intensity of elastic excitation with incident X-rays of π polarization is reduced in comparison with that of σ polarization, and spin–flip excitations are effectively revealed. In addition, the cross-section of L3-edge RIXS for a magnetic excitation is usually larger than that for a phonon excitation35. Because O K-edge RIXS-probe excitations derived from bimagnons42 and phonons43, we performed O K-edge RIXS measurements to probe the phonons of Fe3O4. Our data shown in Supplementary Fig. 4 reveal an excitation at 70 meV in the O K-edge RIXS, indicating that the observed 90-meV feature of the Fe L3-edge RIXS has a small contribution from phonon excitation44,45.
Multiplet RIXS calculations
In order to characterize the origin of the observed excitations, we undertook crystal-field multiplet calculations for the B-site Fe3+ and Fe2+ ionic configurations. See the Methods section, Supplementary Note 2 and Supplementary Figs 5 and 6 for calculation details.
Multiplet calculations carried out for the B-site Fe3+ ions under an exchange molecular field of 90 meV, as shown in Supplementary Fig. 5d, explain the observed excitation energy of 90 meV well. This is consistent with the 100-meV Zeeman splitting induced by the molecular field deduced from the Curie temperature of magnetite and the exchange coupling constants46. This spin–flip energy also agrees with the energy of the nearly dispersionless mode at 80–85 meV observed in inelastic neutron scattering46,47. For an individual Fe3+ site, the intensity of the 90-meV RIXS feature can change under a spin reorientation as magnetic RIXS is sensitive to the spin direction with respect to the incident polarization. However, RIXS measurements of B-sites Fe3+ reflect an average of eight non-equivalent Fe3+. Each of these non-equivalent Fe3+ B-sites can make different contributions to the intensity of the 90-meV feature, and our measured RIXS spectra suggest that these changes are beyond our experimental sensitivity. Although we cannot totally rule out phonon contributions, the 90-meV L3-edge RIXS excitation is best explained as a result of spin–flip excitations of Fe3+ ions, like magnetic excitations observed in the RIXS of Fe pnictide superconductors36, cuprates30,37,40 and nickelates38,41.
The ground state of the octahedral Fe2+ ion is a high-spin 5T2g state with S=2. According to Hund’s rule, out of the six 3d electrons of the Fe2+ ion, five 3d electrons occupy spin-up states  ; the remaining one electron occupies one of the three spin-down orbitals
; the remaining one electron occupies one of the three spin-down orbitals  . When the spin–orbit effect of 3d electrons couple a pseudo-orbital angular momentum
. When the spin–orbit effect of 3d electrons couple a pseudo-orbital angular momentum  to S=2, the 5T2g state splits into three manifolds of pseudo-angular momenta
to S=2, the 5T2g state splits into three manifolds of pseudo-angular momenta  and 3. That is, there are effectively 15 separate states from Fe2+, as the 5T2g ground state is split by the combination of these interactions. For the broad 200-meV RIXS feature associated with the octahedral Fe2+ states, the excitation energy is too large to be explained in terms of spin–flip excitations only. We carefully checked the effect of the local Jahn-Teller distortion to explain the energy of the observed excitations to understand the nature of this feature. From an extensive set of RIXS calculations of Fe2+ with varied tetragonal distortions as shown in Supplementary Fig. 6, we found that the average RIXS spectrum calculated using Hex=90 meV and
and 3. That is, there are effectively 15 separate states from Fe2+, as the 5T2g ground state is split by the combination of these interactions. For the broad 200-meV RIXS feature associated with the octahedral Fe2+ states, the excitation energy is too large to be explained in terms of spin–flip excitations only. We carefully checked the effect of the local Jahn-Teller distortion to explain the energy of the observed excitations to understand the nature of this feature. From an extensive set of RIXS calculations of Fe2+ with varied tetragonal distortions as shown in Supplementary Fig. 6, we found that the average RIXS spectrum calculated using Hex=90 meV and  =−22, −26 and −30 meV explains the measured spectrum most satisfactorily, as demonstrated in Supplementary Fig. 5f. Figure 3a shows the calculated low-energy RIXS excitations of Fe2+ in the form of incident photon energy versus energy-loss maps. The calculated RIXS obtained by including the tetragonal distortion, exchange interaction and 3d spin–orbit coupling matches fairly well with the experimental data.
=−22, −26 and −30 meV explains the measured spectrum most satisfactorily, as demonstrated in Supplementary Fig. 5f. Figure 3a shows the calculated low-energy RIXS excitations of Fe2+ in the form of incident photon energy versus energy-loss maps. The calculated RIXS obtained by including the tetragonal distortion, exchange interaction and 3d spin–orbit coupling matches fairly well with the experimental data.
(a) Calculated RIXS intensity map of B-site Fe2+ by using Hex=90 meV,  meV and the 3d spin–orbit coupling
meV and the 3d spin–orbit coupling  meV. The resonance photon energy of Fe2+ is set to the experimental resonance energy 707.5 eV. The core–hole lifetime width is set to 200 meV, and the final-state lifetime width is set to 10 meV. This calculated intensity map presents the average RIXS intensity for the magnetic easy axis along the [100], [010] and [001] directions, and are plotted after Gaussian broadening of width 500 and 80 meV for the incident photon energy and the energy loss, respectively. (b) A magnified intensity map of RIXS measurements of single-crystal Fe3O4 extracted from Fig. 2b. (c) Comparison of measured (expt) and calculated (calc) RIXS spectra. Open circles are measurements with incident X-rays of 707 eV at 80 K; the solid line presents the calculated RIXS spectra of incident X-ray energy 707.5 eV.
meV. The resonance photon energy of Fe2+ is set to the experimental resonance energy 707.5 eV. The core–hole lifetime width is set to 200 meV, and the final-state lifetime width is set to 10 meV. This calculated intensity map presents the average RIXS intensity for the magnetic easy axis along the [100], [010] and [001] directions, and are plotted after Gaussian broadening of width 500 and 80 meV for the incident photon energy and the energy loss, respectively. (b) A magnified intensity map of RIXS measurements of single-crystal Fe3O4 extracted from Fig. 2b. (c) Comparison of measured (expt) and calculated (calc) RIXS spectra. Open circles are measurements with incident X-rays of 707 eV at 80 K; the solid line presents the calculated RIXS spectra of incident X-ray energy 707.5 eV.
Discussion
In comparison with the magnified intensity map of RIXS measurements shown in Fig. 3b, calculations using a molecular field Hex=90 meV and  =−26±4 meV reproduce the energy-loss features suitably. For the 200-meV excitation, the experimental resonance starts at an energy lower than that of the resonant quasi-elastic scattering of Fe2+ and its energy range is broad, while the calculated resonance starts at a higher energy with a narrow range. This discrepancy is attributed to differences in the dynamics of 3d orbitals due to core–hole effects in intermediate states. These effects do not affect the energy loss of excitation spectra because the core holes are filled in the RIXS final state. As is typical of RIXS calculations reported in the literature, our calculations do not include such core–hole effects, and hence do not reproduce the incident energy dependence perfectly, but our calculations correctly reproduce the energy-loss features.
=−26±4 meV reproduce the energy-loss features suitably. For the 200-meV excitation, the experimental resonance starts at an energy lower than that of the resonant quasi-elastic scattering of Fe2+ and its energy range is broad, while the calculated resonance starts at a higher energy with a narrow range. This discrepancy is attributed to differences in the dynamics of 3d orbitals due to core–hole effects in intermediate states. These effects do not affect the energy loss of excitation spectra because the core holes are filled in the RIXS final state. As is typical of RIXS calculations reported in the literature, our calculations do not include such core–hole effects, and hence do not reproduce the incident energy dependence perfectly, but our calculations correctly reproduce the energy-loss features.
Figure 3c presents calculated RIXS spectrum in comparison with measurements of the incident X-ray energy set to 707 eV, at which the 200-meV RIXS feature is most pronounced. The negative value of  signifies that the energy of dxy is lower than that of dyz/dzx, that is, tetragonally distorted Fe2+O6 octahedra with elongated Fe–O bonds in the xy plane. This shows that the tetragonal distortion is directly related to a polaronic distortion of the Fe2+O6 octahedra, which in turn couple to the neighbouring Fe3+O6 octahedra constituting the trimerons, although, as mentioned earlier, they are Jahn-Teller-inactive in the first approximation. Our results are consistent with the locally distorted structure of the FeO6 octahedra and the short-range order above TV observed by X-ray absorption48 and diffuse scattering29. These short-range correlations are polaronic in nature23,26,27,29,49. Because a local molecular field and a tetragonal Jahn-Teller polaronic distortion are required to correctly simulate the excitation energy, the observed spin–orbital excitations are, indeed, magnetic polarons.
signifies that the energy of dxy is lower than that of dyz/dzx, that is, tetragonally distorted Fe2+O6 octahedra with elongated Fe–O bonds in the xy plane. This shows that the tetragonal distortion is directly related to a polaronic distortion of the Fe2+O6 octahedra, which in turn couple to the neighbouring Fe3+O6 octahedra constituting the trimerons, although, as mentioned earlier, they are Jahn-Teller-inactive in the first approximation. Our results are consistent with the locally distorted structure of the FeO6 octahedra and the short-range order above TV observed by X-ray absorption48 and diffuse scattering29. These short-range correlations are polaronic in nature23,26,27,29,49. Because a local molecular field and a tetragonal Jahn-Teller polaronic distortion are required to correctly simulate the excitation energy, the observed spin–orbital excitations are, indeed, magnetic polarons.
The magnitude of obtained  is comparable with the 3d spin–orbit coupling strength, and thus confirms the observation of the unquenched orbital moment50, which is known from work on Fe2+ impurities in MgO thin films51. These results are also consistent with conclusions of band-structure calculations using the monoclinic P2/c crystal structure of magnetite9 (see Supplementary Note 3 and Supplementary Fig. 7), which give an energy splitting ∼50 meV between minority-spin dxy and dyz/dzx bands at the Γ point, conforming to the deduced
is comparable with the 3d spin–orbit coupling strength, and thus confirms the observation of the unquenched orbital moment50, which is known from work on Fe2+ impurities in MgO thin films51. These results are also consistent with conclusions of band-structure calculations using the monoclinic P2/c crystal structure of magnetite9 (see Supplementary Note 3 and Supplementary Fig. 7), which give an energy splitting ∼50 meV between minority-spin dxy and dyz/dzx bands at the Γ point, conforming to the deduced  .
.
We also performed RIXS measurements above the Verwey transition and found that the spin–orbital excitations driven by polaronic distortion do exist in the cubic phase of Fe3O4 at high temperatures as shown in Fig. 2e and Supplementary Fig. 8. Figure 4 plots the temperature-dependent RIXS spectra with the incident X-ray energy set to the pre-edge absorption at 706 eV, an incident X-ray energy at which the elastic component is weak and the RIXS arises predominantly from octahedral Fe2+ ions with a negligible contribution from Fe3+. The temperature-dependent results show that, when the temperature is varied across TV, the spin–orbital excitation of 200 meV does not abruptly change its intensity and persists at least up to 550 K, albeit with a gradual decrease above 350 K. We interpret this as a gradual weakening of the polarons. RIXS results shown here serve as a fast probe to snapshot the dynamic lattice–spin–orbital excitations of Fe3O4. These temperature-dependent RIXS results indicate that the FeO6 octahedra are already locally distorted in the cubic phase of magnetite, in good agreement with the existence of the short-range correlations in the lattice structure above TV. The temperature dependence of these distortions follows that of the magnetization of magnetite, suggesting short-range ordering of the Jahn-Teller distortion, which gets weakened as the temperature approaches the Curie temperature TC, and providing further evidence for magnetic polarons. These observations suggest that the local distortion in the cubic phase could be attributed to the precursor of the monoclinic phase across the Verwey transition.
(a,b) RIXS spectra after the subtraction of the elastic component at selected temperatures. The spectra were recorded with the incident X-ray energy set to 706 eV. (c) Plot of the integrated 200-meV RIXS intensity versus temperature. The data were analysed by subtracting the elastic component from the measured spectrum and normalizing to the intensity of the dd excitation feature at 2.8 eV (see Supplementary Fig. 9). The dashed line indicates the Verwey transition temperature TV. The RIXS data comprise an average of four runs of experimental results. The error bars are deduced from the average value of variations in the spectral intensity of four sets of measurements.
To summarize, our results demonstrate the usefulness of RIXS to unravel the local electronic structure of a mixed-valence compound by selecting the energy and polarization of incident X-rays. We revealed dd excitons in magnetite that have an energy centroid 200 meV and arise from polaronic distortion-driven spin–orbital excitations, which are best explained as magnetic polarons. We also applied crystal-field multiplet calculations to obtain the t2g crystal field  =−26±4 meV induced by the tetragonal Jahn-Teller distortion. These results are consistent with the mechanism of ordering trimerons for the Verwey transition. It would be interesting to carry out RIXS experiments with an improved energy resolution to study the change of spin–orbital excitations across the Verwey transition.
=−26±4 meV induced by the tetragonal Jahn-Teller distortion. These results are consistent with the mechanism of ordering trimerons for the Verwey transition. It would be interesting to carry out RIXS experiments with an improved energy resolution to study the change of spin–orbital excitations across the Verwey transition.
Methods
RIXS measurements
Using the AGM–AGS spectrometer at beamline 05A1 of the Taiwan Light Source31, we measured RIXS on a single-crystal Fe3O4(001) at incident photon energies set to specific energies about the L3(2p3/2→3d) absorption edge of Fe. See Supplementary Fig. 2a for the scattering geometry. Both the scattering angle φ defined as the angle between the incident and the scattered X-rays, and the incident angle θ from the crystal ab plane, were variable. The polarization of the incident X-ray was switchable between π and σ polarizations, that is, the polarization within and perpendicular to the scattering plane, respectively, and the polarization of scattered X-rays was not analysed. The energy bandwidth of the incident X-rays was 500 meV, and the total RIXS energy resolution was ∼80 meV because the energy compensation method was used to ensure a high-resolution measurement in the energy-loss scheme31. The beam diameter of incident X-ray at the sample is ∼0.5 mm.
Sample preparation
Single-crystal growth of magnetite was carried out in an infrared image furnace in high-purity argon gas (99.999% purity) atmosphere. Measurements of the temperature-dependent specific heat and resistivity of the synthesized magnetite crystal showed that it exhibits a sharp first-order Verwey transition at TV=122 K. The synthesized single crystal has a chemical composition of Fe3(1−δ)O4 with |δ|≤0.00018, indicative of a nearly ideal chemical stoichiometry. See Supplementary Figs 10 and 11 for the sample characterization.
Multiplet calculations
We undertook crystal-field multiplet RIXS calculations of B-site Fe2+ and Fe3+ using CTM4RIXS52 and MISSING (Dallera and Gusmeroli http://www.esrf.eu/computing/scientic/MISSING/) with the scattering angle 90° and the magnetization axis perpendicular to the scattering plane or in the scattering plane with angles 20° or 70° to the incident beam. The polarization of incident X-rays was selected to be π-polarized. Since the polarization of scattered X-rays was not analysed in the measurements, we summed calculated RIXS spectra of scattered X-rays with σ and π polarizations. We used a Lorentzian broadening 0.2 eV for the lifetime width of the intermediate states. The calculated spectra are obtained as an average of the spectra calculated for magnetic domains with the easy axis along the [100], [010] and [001] directions. The crystal-field parameter 10Dq was set to 1.13 eV, and the Slater integrals were reduced to 79% of their atomic values for accurately reproducing the dd excitation energies.
Data availability
The data that support the findings of this study are available from the corresponding authors on request.
Additional information
How to cite this article: Huang, H. Y. et al. Jahn-Teller distortion driven magnetic polarons in magnetite. Nat. Commun. 8, 15929 doi: 10.1038/ncomms15929 (2017).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Bragg, W. H. The structure of magnetite and the spinels. Nature 95, 561–561 (1915).
Verwey, E. J. W. Electronic conduction of magnetite and its transition point at low temperatures. Nature 144, 327–328 (1939).
Walz, F. The Verwey transition--a topical review. J. Phys. Condens. Matter 14, R285–R340 (2002).
De Jong, S. et al. Speed limit of the insulator-metal transition in magnetite. Nat. Mater. 12, 882–886 (2013).
Almeida, T. P. et al. Visualized effect of oxidation on magnetic recording fidelity in pseudo-single-domain magnetite particles. Nat. Commun. 5, 5154 (2014).
Veintemillas-Verdaguer, S. et al. Magnetic nanocrsyatls for biomedical applications. Prog. Cryst. Growth Charact. Mater. 60, 80–86 (2014).
Wright, J. P., Attfield, J. P. & Radaelli, P. G. Long range charge ordering in magnetite below the Verwey transition. Phys. Rev. Lett. 87, 266401 (2001).
Wright, J. P., Attfield, J. P. & Radaelli, P. G. Charge ordered structure of magnetite below the Verwey transition. Phys. Rev. B 66, 214422 (2002).
Jeng, H.-T., Guo, G. Y. & Huang, D. J. Charge-orbital ordering and Verwey transition in magnetite. Phys. Rev. Lett. 93, 156403 (2004).
Leonov, I., Yaresko, A. N., Antonov, V. N., Korotin, M. A. & Anisimov, V. I. Charge and orbital order in Fe3O4 . Phys. Rev. Lett. 93, 146404 (2004).
Jeng, H. T., Guo, G. Y. & Huang, D. J. Charge-orbital ordering in low-temperature structures of magnetite: GGA+ U investigations. Phys. Rev. B 74, 195115 (2006).
Huang, D. J. et al. Charge-orbital ordering and Verwey transition in magnetite measured by resonant soft X-ray scattering. Phys. Rev. Lett. 96, 096401 (2006).
Nazarenko, E. et al. Resonant X-ray diffraction studies on the charge ordering in magnetite. Phys. Rev. Lett. 97, 056403 (2006).
Schlappa, J. et al. Direct observation of t2g orbital ordering in magnetite. Phys. Rev. Lett. 100, 026406 (2008).
Senn, M. S., Wright, J. P. & Attfield, J. P. Charge order and three-site distortions in the Verwey structure of magnetite. Nature 481, 173–176 (2012).
Senn, M. S., Loa, I., Wright, J. P. & Attfield, J. P. Electronic orders in the Verwey structure of magnetite. Phys. Rev. B 85, 125119 (2012).
Senn, M. S., Wright, J. P., Cumby, J. & Attfield, J. P. Charge localization in the Verwey structure of magnetite. Phys. Rev. B 92, 024104 (2015).
Ihle, D. & Lorenz, B. Small-polaron band versus hopping conduction in Fe3O4 . J. Phys. C 18, L647–L650 (1985).
García, J. et al. Resonant ‘forbidden’ reflections in magnetite. Phys. Rev. Lett. 85, 578–581 (2000).
Subías, G. et al. Magnetite, a model system for mixed-valence oxides, does not show charge ordering. Phys. Rev. Lett. 93, 156408 (2004).
Piekarz, P., Parlinski, K. & Oleś, A. M. Mechanism of the Verwey transition in magnetite. Phys. Rev. Lett. 97, 156402 (2006).
Hoesch, M. et al. Anharmonicity due to electron-phonon coupling in magnetite. Phys. Rev. Lett. 110, 207204 (2013).
Park, S. K., Ishikawa, T. & Tokura, Y. Charge-gap formation upon the Verwey transition in Fe3O4 . Phys. Rev. B 58, 3717–3720 (1998).
Chainani, A., Yokoya, T., Morimoto, T., Takahashi, T. & Todo, S. High-resolution photoemission spectroscopy of the Verwey transition in Fe3O4 . Phys. Rev. B 51, 17976–17979 (1995).
Park, J. H., Tjeng, L. H., Allen, J. W., Metcalf, P. & Chen, C. T. Single-particle gap above the Verwey transition in Fe3O4 . Phys. Rev. B 55, 12813–12817 (1997).
Schrupp, D. et al. High-energy photoemission on Fe3O4: small polaron physics and the Verwey transition. Europhys. Lett. 70, 789–795 (2005).
Taguchi, M. et al. Temperature dependence of magnetically active charge excitations in magnetite across the Verwey transition. Phys. Rev. Lett. 115, 256405 (2015).
Anderson, P. W. Ordering and antiferromagnetism in ferrites. Phys. Rev. 102, 1008–1013 (1956).
Bosak, A. et al. Short-range correlations in magnetite above the Verwey temperature. Phys. Rev. X 4, 011040 (2014).
Ament, L. J. P., van Veenendaal, M., Devereaux, T. P., Hill, J. P. & van den Brink, J. Resonant inelastic x-ray scattering studies of elementary excitations. Rev. Mod. Phys. 83, 705–767 (2011).
Lai, C. H. et al. Highly efficient beamline and spectrometer for inelastic soft X-ray scattering at high resolution. J. Synchrotron Radiat. 21, 325–332 (2014).
Kuiper, P., Searle, B. G., Duda, L. C., Wolf, R. M. & Van der Zaag, P. J. Fe L2,3 linear and circular magnetic dichroism of Fe3O4 . J. Electron. Spectrosc. Relat. Phenom. 86, 107–113 (1997).
Chen, J. et al. Magnetic circular dichroism in Fe 2p resonant photoemission of magnetite. Phys. Rev. B 69, 085107 (2004).
Arenholz, E., van der Laan, G., Chopdekar, R. V. & Suzuki, Y. Anisotropic X-ray magnetic linear dichroism at the Fe L2,3 edges in Fe3O4 . Phys. Rev. B 74, 094407 (2006).
Braicovich, L. et al. Magnetic excitations and phase separation in the underdoped La2−xSrx CuO4 superconductor measured by resonant inelastic X-ray scattering. Phys. Rev. Lett. 104, 077002 (2010).
Zhou, K. J. et al. Persistent high-energy spin excitations in iron-pnictide superconductors. Nat. Commun. 4, 1470 (2013).
Huang, H. Y. et al. Raman and fluorescence characteristics of resonant inelastic X-ray scattering from doped superconducting cuprates. Sci. Rep. 6, 19657 (2016).
de Groot, F. M. F., Kuiper, P. & Sawatzky, G. A. Local spin-flip spectral distribution obtained by resonant x-ray Raman scattering. Phys. Rev. B 57, 14584–14587 (1998).
van Veenendaal, M. Polarization dependence of L-and M-edge resonant inelastic X-ray scattering in transition-metal compounds. Phys. Rev. Lett. 96, 117404 (2006).
Jia, C. J. et al. Persistent spin excitations in doped antiferromagnets revealed by resonant inelastic light scattering. Nat. Commun. 5, 3314 (2014).
Haverkort, M. W. Theory of resonant inelastic X-ray scattering by collective magnetic excitations. Phys. Rev. Lett. 105, 167404 (2010).
Bisogni, V. et al. Bimagnon studies in cuprates with resonant inelastic X-ray scattering at the O K edge. I. Assessment on La2CuO4 and comparison with the excitation at Cu L3 and Cu K edges. Phys. Rev. B 85, 214527 (2012).
Lee, W. S. et al. Role of lattice coupling in establishing electronic and magnetic properties in quasi-one-dimensional cuprates. Phys. Rev. Lett. 110, 265502 (2013).
Gasparov, L. V. et al. Infrared and Raman studies of the Verwey transition in magnetite. Phys. Rev. B 62, 7939–7944 (2000).
Gasparov, L. V. et al. Magnetite: Raman study of the high-pressure and low-temperature effects. J. Appl. Phys. 97, 10A922 (2005).
McQueeney, R. J. et al. Investigation of the presence of charge order in magnetite by measurement of the spin wave spectrum. Phys. Rev. B 73, 174409 (2006).
McQueeney, R. J. et al. Zener double exchange from local valence fluctuations in magnetite. Phys. Rev. Lett. 99, 246401 (2007).
Subías, G., García, J. & Blasco, J. EXAFS spectroscopic analysis of the Verwey transition in Fe3O4 . Phys. Rev. B 71, 155103 (2005).
Ihle, D. & Lorenz, B. Small-polaron conduction and short-range order in Fe3O4 . J. Phys. C 19, 5239–5251 (1986).
Huang, D. J. et al. Spin and orbital magnetic moments of Fe3O4 . Phys. Rev. Lett. 93, 077204 (2004).
Haupricht, T. et al. Local electronic structure of Fe2+ impurities in MgO thin films: temperature-dependent soft X-ray absorption spectroscopy study. Phys. Rev. B 82, 035120 (2010).
Stavitski, E. & de Groot, F. M. F. The CTM4XAS program for EELS and XAS spectral shape analysis of transition metal L edges. Micron 41, 687–694 (2010).
Acknowledgements
We thank A. Fujimori, J. Paul Attfield, Jeroen van de Brink, Sumio Ishihara, Chun-Fu Chang, Maurits Haverkort and Hebatalla Elnaggar for valuable discussions. We acknowledge Martin Beye for sharing unpublished results with us. This work was supported in part by the Ministry of Science and Technology of Taiwan under Grant No. 103-2112-M-213-008-MY3. J.-S.Z. was supported by the DOD-ARMY grant (W911NF-16-1-0559) in USA. J.-G.P. was supported by the research programme of the Institute for Basic Science (IBS-R009-G1) in Korea.
Author information
Authors and Affiliations
Contributions
All authors made significant contributions. H.Y.H., Z.Y.C., W.B.W., J.O. and A.S. performed RIXS measurements. H.Y.H., R.-P.W. and F.M.F.d.G. performed multiplet calculations. H.-T.J. and G.Y.G. performed band-structure calculations. C.T.C. designed the RIXS beamline and spectrometer. Z.-Y.L and J.-S.Z. synthesized and prepared the magnetite single crystals. D.J.H., H.Y.H., F.M.F.d.G., A.C., J.-S.Z., J.-G.P. and L.H.T. analysed the data, discussed the results and wrote the paper. D.J.H. is responsible for project planning.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Huang, H., Chen, Z., Wang, RP. et al. Jahn-Teller distortion driven magnetic polarons in magnetite. Nat Commun 8, 15929 (2017). https://doi.org/10.1038/ncomms15929
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms15929
This article is cited by
-
Resonant inelastic X-ray scattering as a probe of Jeff = 1/2 state in 3d transition-metal oxide
npj Quantum Materials (2022)
-
Polarons in materials
Nature Reviews Materials (2021)
-
Discovery of the soft electronic modes of the trimeron order in magnetite
Nature Physics (2020)
-
Sub-lattice of Jahn-Teller centers in hexaferrite crystal
Scientific Reports (2020)
-
Temperature dependence of spherical electron transfer in a nanosized [Fe14] complex
Nature Communications (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.


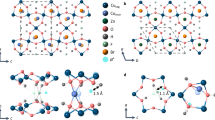

 crystal field. A trimeron is indicated with a dashed oval. The elongation of the four Fe–O bonds in the xy plane are indicated with arrows.
crystal field. A trimeron is indicated with a dashed oval. The elongation of the four Fe–O bonds in the xy plane are indicated with arrows.

