Abstract
Terrestrial ecosystems play a significant role in the global carbon cycle and offset a large fraction of anthropogenic CO2 emissions. The terrestrial carbon sink is increasing, yet the mechanisms responsible for its enhancement, and implications for the growth rate of atmospheric CO2, remain unclear. Here using global carbon budget estimates, ground, atmospheric and satellite observations, and multiple global vegetation models, we report a recent pause in the growth rate of atmospheric CO2, and a decline in the fraction of anthropogenic emissions that remain in the atmosphere, despite increasing anthropogenic emissions. We attribute the observed decline to increases in the terrestrial sink during the past decade, associated with the effects of rising atmospheric CO2 on vegetation and the slowdown in the rate of warming on global respiration. The pause in the atmospheric CO2 growth rate provides further evidence of the roles of CO2 fertilization and warming-induced respiration, and highlights the need to protect both existing carbon stocks and regions, where the sink is growing rapidly.
Similar content being viewed by others
Introduction
The oceans and the terrestrial biosphere remove about 45% of the CO2 emitted by human activities each year1. The rate of CO2 uptake is not constant, however, and varies greatly from year to year in response to changes in the atmosphere (for example, El Niño events, volcanic eruptions and natural climate variability). The largest component of the year-to-year variability in CO2 uptake is contributed by processes on land2,3. Any increase or decrease in terrestrial uptake thus generates a feedback to the atmosphere4, which affects the growth rate of atmospheric CO2, and the rate at which the climate warms.
Over the past 50 years, the amount of CO2 absorbed by the oceans and terrestrial biosphere annually has more than doubled1,5,6,7,8. The enhanced carbon sink has been attributed to increased ocean9 and terrestrial uptake1,6,7,8,10, and has occurred despite an increase in the severity and intensity of regional disruptions to ecosystems in recent years, such as extensive droughts, wildfires and insect damage11,12,13,14. On land, reports suggest a decline in the tropical sink15,16, increased plant mortality17,18 and decreased plant productivity due to droughts and extreme events19,20. In contrast, others report that elevated CO2 has led to increased photosynthesis8 and a greening of the biosphere21,22. The relative contributions of the different processes involved in the terrestrial sink enhancement remain unquantified. Global warming over vegetated land notably slowed since the start of the twenty-first century23, while atmospheric CO2 concentrations continue to rise, providing an opportunity to test the relative roles of various processes in the enhancement of terrestrial carbon uptake, and examine the implications of enhanced carbon uptake for the growth rate of atmospheric CO2.
Here we use extensive ground observations of earth–atmosphere CO2 exchange, atmospheric CO2 observations and satellite observations of vegetation, along with an ensemble of 10 prognostic dynamic global vegetation models (DGVMs), and a diagnostic process-based modelling approach, to examine the causes of the long-term enhancement of terrestrial carbon uptake and consequences for the growth rate of atmospheric CO2. Our analysis suggests that enhanced carbon uptake is due to the combined effects of rising CO2 on photosynthesis (the CO2 fertilization effect) and, in the past decade, a slowdown in the rate of warming on global respiration. The continued enhancement of the terrestrial carbon sink during the recent slowdown in global warming led to a pause in the atmospheric CO2 growth rate, and a decline in the fraction of anthropogenic emissions that remains in the atmosphere.
Results
Slowing of the growth rate of atmospheric CO2
Changes in the residual terrestrial carbon sink affect the proportion of anthropogenic emissions that remain in the atmosphere (the airborne fraction), and thus the growth rate of atmospheric CO2. Our analysis suggests that the airborne fraction increased steadily from the 1960s to the 1990s (1.8% per year, P=0.03; Fig. 1b), albeit with large interannual variability reflecting year-to-year variability in the terrestrial sink4. Since the start of the twenty-first century, however, the airborne fraction has been declining (−2.2% per year, P=0.07; Fig. 1b), despite the rapid increase in anthropogenic emissions (Fig. 1b). Changes in the airborne fraction are reflected in the atmospheric CO2 growth rate. For the three decades from the start of the measurement record in 1959, the atmospheric CO2 growth rate increased from 0.75 to 1.86 p.p.m. per year (Fig. 1a). However, for the period 2002–2014 there has been no significant increase in the growth rate of CO2 (Fig. 1a and Supplementary Fig. 1). The decline in the airborne fraction since the start of the twenty-first century has therefore been sufficiently large as to result in a pause in the rate of increase of the atmospheric CO2 growth rate (Fig. 1a). Atmospheric growth rates have deviated significantly from predictions of a linear model of atmospheric CO2 concentrations and anthropogenic emissions since 2002 (Supplementary Fig. 1), suggesting a nonlinear increase in the global sink strength.
(a) Observed (solid black line) and modelled (DGVM ensemble—mean (dashed black line) and s.d. (orange area)) changes in the atmospheric CO2 growth rate from 1960 to 2012. The vertical grey line (2002) indicates the point of structural change identified using a linear modelling analysis. The red lines indicate a significant increasing trend from 1959 to 1990 (solid red) and 1959 to 2002 (dashed red) (P<0.1), with no trend evident between 2002 and 2014 (blue). All trends are estimated using the non-parametric Mann–Kendall Tau trend test with Sen’s method. The grey area represents the underlying 5-year dynamic (mean±1 s.d.), estimated using SSA. (b) Fossil fuel emissions (black dashed line) and the fraction of CO2 emissions, which remain in the atmosphere each year (black dots, airborne fraction). Lines indicate significant long-term trends over the periods 1959–1988 (red, increasing) and 2002–2014 (blue, decreasing) at P<0.1. The red dashed line shows a slight increasing trend between 1959 and 2002 (P=0.18). The grey area represents the underlying 5-year dynamic (mean±1 s.d.), estimated using singular spectrum analysis.
Enhancement of the terrestrial carbon sink
Global simulations, from the ensemble of DGVMs included in the Global Carbon Project1, and a satellite-based estimate of the terrestrial carbon cycle (see Methods), suggest that the net residual terrestrial carbon sink (the total annual accumulation of carbon in the terrestrial biosphere after accounting for the net effect of land use change) has steadily increased over recent decades, from about 1–2 PgC per year in the 1950s to 2–4 PgC per year in the 2000s (Fig. 2). These model and satellite-based estimates are consistent with recent decadal estimates of the residual terrestrial carbon sink compiled by the Intergovernmental Panel on Climate Change, which show terrestrial uptake increasing from roughly 1.5 PgC per year during the 1980s to 2.6 PgC per year in the 2000s (ref. 24) (Fig. 2), and estimates from the Global Carbon Project (Supplementary Fig. 2).
Estimates of the global terrestrial residual carbon sink from 1901 to 2014. Light grey dots are the historical net residual land CO2 sink, estimated by the Global Carbon Project (GCP). Orange shaded areas represent the Global Carbon Project dynamic global vegetation ensemble (annual mean, solid black line, and s.d., orange area) from 10 dynamic global vegetation models (DGVMs). Black dots represent annual values from the satellite-driven diagnostic land surface model, and the grey area represents the associated long-term temporal dynamics (mean±1 s.d.) estimated using singular spectrum analysis. Horizontal bars represent the mean residual land sink values reported by the Intergovernmental Panel on Climate Change (IPCC) 2013, for the periods 1980–1995 (dark green) and 1995–2009 (light green).
The slowing of the growth rate of atmospheric CO2 between 2002 and 2014 (Fig. 1a and Supplementary Fig. 1) coincides with a period during which global temperature increases over vegetated land also slowed markedly23 (Fig. 3 and Supplementary Fig. 3, note recent reports suggest continued warming over oceans25). Since the start of the century, global temperatures over vegetated land increased at a rate of 0.1 °C per decade, compared with a rate of 0.32 °C per decade in the previous two decades (Fig. 3). Satellite-driven estimates of the carbon cycle suggest that the slowdown in global warming led to a slowdown in temperature-driven ecosystem respiration of roughly 60% (Fig. 3). The global slowdown in warming exhibited specific regional differences (Supplementary Fig. 4). In particular, although a slowdown in warming was evident over the western United States, and much of Asia, other regions such as the eastern United States, eastern Europe and Siberia experienced accelerated warming (Supplementary Fig. 4). The photosynthesis–respiration (PR) model results suggest that, on a global scale, the lower temperature-driven increase in Reco in the past decade, and the continued stimulation of global gross primary production (GPP, see below), likely combined to generate the reported large enhancement of global net ecosystem production (NEP).
Trends in (a) ecosystem respiration (Reco) derived from satellite-driven estimates of the carbon cycle (photosynthesis-respiration (PR) model, see methods), and (b) global warming over vegetated land for the periods of 1980–2000 and 2000–2012. Trends for both periods were estimated using the Sen slope from Kendall's Tau-b method on de-seasonalized monthly data. Error bars represent 95% confidence intervals of the trend.
Effects of CO2 on photosynthesis and respiration
Although a lack of temperature increases likely contributed to the slowdown in the growth rate of atmospheric CO2 over the past decade (Fig. 3), results from the DGVM ensemble suggest that an increasing atmospheric CO2 concentration was the primary driver of the enhanced uptake over the past century (Fig. 4). Atmospheric CO2 concentrations increased from roughly 290 p.p.m. at the start of the twentieth century to 400 p.p.m. by 2015, with a pronounced effect on global GPP (Fig. 4b), and a large but lesser effect on Reco (Fig. 4c). The DGVM simulations suggest that increasing atmospheric CO2 concentrations led to an increase in global annual GPP of 18±2 PgC (mean±1 s.d.) since 1900 (Fig. 4b). Elevated CO2 also increased Reco due to the carbon supplied through photosynthesis (Fig. 4c). Empirical evidence for this link has been reported across a range of ecosystems: grasslands26; crops27; and forests28. The DGVM results suggest an increase of 13±4 PgC in global annual Reco over the past century due to increasing CO2 (Fig. 4c). The largest increases in absolute terms were located in the tropics for both GPP and Reco (Fig. 5), with a lesser contribution from northern temperate and boreal regions.
Model estimates of the extent to which long-term changes in different forcing factors are responsible for the long-term change in net ecosystem production (NEP) (a,d), gross primary production (GPP) (b,e) and ecosystem respiration (Reco; c,f), where NEP=GPP−Reco. Shaded areas in a–c represent the mean and s.d. from the TRENDY ensemble of dynamic global vegetation model (DGVM) simulations with varying CO2 (green) or climate (red) only. Dashed lines in a–c show the effect of changes in vegetation (or the fraction of absorbed radiation (fAPAR), blue), and water availability (Alpha, black) estimated using a satellite-driven coupled photosynthesis-respiration (PR) model. (d–f) The mean change associated with each driver between the periods 1901–1915 and 1995–2010.
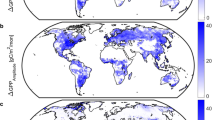
(a–c) The latitudinal distribution of the effect of changes in different forcing factors on (a) net ecosystem production (NEP), (b) gross primary production (GPP) and (c) ecosystem respiration (Reco). Shaded areas represent the mean and s.d. from the TRENDY ensemble of dynamic global vegetation models (DGVM) simulations with varying only CO2 (green) or climate (red). Dashed lines in a–c show the effect of changes in vegetation (or the fraction of absorbed radiation (fAPAR), blue) and water availability (Alpha, black) estimated using a diagnostic coupled photosynthesis-respiration (PR) model. (d–i) The spatial distribution of the influence of increasing atmospheric CO2 and changes in global climate on total rates of NEP (d,g), GPP (e,h) and total ecosystem respiration (f,i) in gC m−2 per year. Effects are estimated based on the difference between the 15-year periods of 1901–1915 and 1995–2010.
Effects of changes in vegetation cover and climate
The direct effects of changes in atmospheric CO2 on both photosynthesis and respiration have had a larger impact on the terrestrial carbon sink than changes in climate, vegetation cover and water availability (Fig. 4). The effects of changes in climate are particularly evident in the 1980s and 1990s, when temperature increases were most pronounced (Fig. 3), with the largest impacts at higher latitudes (Fig. 5). Overall, the impact of changes in climate on global net carbon uptake is uncertain, due to the small magnitude of the effect compared with differences between the DGVM models. It is worth noting however that there is a strong indirect effect of temperature through the alleviation of temperature limitations to growth in colder regions, and the extension of the growing season, observable as an increase in vegetation cover in satellite observations.
A global greening of the Earth’s surface has been reported in satellite observations21,22, which has been attributed to both the direct effect of temperature changes and the indirect effect of CO2 fertilization21,22. The results from our satellite-based carbon cycle model suggest that this has increased the residual terrestrial sink by about 0.66 PgC per decade over the past three decades (Fig. 4). The largest effects are evident at northern latitudes, where warming over the past century has diminished temperature limitations (Fig. 5). The effect of greening on the global carbon cycle was secondary to the direct effect of increasing atmospheric CO2 on GPP and Reco, and that of increasing temperatures on Reco (Fig. 4).
Drought has been suggested to increase under future warming11,29, due to the effect of higher global temperatures on potential evapotranspiration rates, leading to an expected decrease in green vegetation in some regions30. We do not detect a change in soil moisture availability using global climate data (Fig. 4), and attribute only a small fraction of the long-term change in global carbon uptake to changes in the water cycle (Fig. 5). The lack of a global change in soil moisture availability is in line with recent reports14,31 (but see ref. 29). Although global warming is often associated with an increase in the prevalence of drought, global precipitation increases with global temperatures32. Collectively, this suggests that there has been little to no change in the prevalence of drought over recent decades on a global scale14,31 despite the occurrence of large regional drought events (for example, ref. 33).
Discussion
The ongoing enhancement of CO2 uptake by the terrestrial biosphere is slowing the rate atmospheric CO2 accumulation. Both theory and observations suggest CO2 fertilization as a likely, dominant explanation of the global enhancement8,34, though alternative perspectives exist35. Our results suggest that the direct effect of CO2 on both photosynthesis and respiration is much larger than the indirect effect of global land surface greening21 and global changes in soil moisture18. In the most recent decade, results suggest that terrestrial uptake has increased as a consequence of a slowdown in the rate of global warming over vegetated land, resulting in a decline in the rate of increase in global respiration. We show that the combined effect of CO2 fertilization and the slowdown in warming has been sufficiently large to decrease the airborne fraction of anthropogenic CO2 emissions and slow the growth rate of atmospheric CO2 despite increasing anthropogenic emissions. Model simulations predicted largest changes to the terrestrial carbon sink in both tropical ecosystems, due to the effect of CO2 on photosynthesis, and high-latitude ecosystems, due to land surface greening and the effects of both CO2 and temperature on photosynthesis and respiration. It is important to note that the land sink is due to the lag between carbon uptake through photosynthesis and release through respiration. Although the sensitivity of GPP to rising CO2 is expected to decline as CO2 concentrations rise (see Methods), the observed enhancement will thus likely persist into the future as long as the stimulation of productivity by elevated CO2 continues to outweigh net carbon releases from warming. The slowdown in global warming is expected to be temporary23 however and may already have ended with the strong El Niño Southern Oscillation of 2015 and 2016, with subsequent consequences for the growth rate of atmospheric CO2 (ref. 36). The likely continuation of warming in the coming decades37 suggests further future increases in net carbon releases.
Other factors not examined here could contribute to changes in the residual terrestrial sink, including nutrient deposition38, changes in diffuse light39 and ozone concentrations40. Nutrient deposition has been reported to increase forest growth, particularly in areas of high N-deposition, primarily north-eastern United States, Western Europe and north-eastern China. Recent studies have estimated the effect of N-deposition on global forest growth on the order of 0.3% per year38. Much less is known about the effect of N-deposition on decomposition processes, however, with recent reports suggesting that N-deposition inhibits respiration from forest soils41. Modelling studies42,43 indicate an increase in global annual terrestrial uptake of about 0.2–0.24 PgC in recent decades due to anthropogenic N-deposition, which is an order of magnitude lower than our estimates of recent changes in carbon uptake due to observed changes in fraction of absorbed photosynthetically active radiation (fAPAR) alone (Fig. 4). Diffuse light changes have also been reported and are estimated to have increased uptake between 1960 and 1980 by 0.44 PgC per year globally39. The effect of ozone on the terrestrial carbon cycle is uncertain, due to unknowns regarding plant-specific sensitivities to ozone40 and the effect of canopy structure44. Ultimately, there are a myriad of factors that influence the carbon cycle, particularly at regional scales. Our analysis suggests however that CO2 and temperature are most likely the dominant factors driving global long-term change.
Despite the decline in the airborne fraction and the resulting pause in the growth rate of atmospheric CO2, the ultimate outcome regarding the pace and magnitude of climate change depends heavily on future emission pathways. CO2 emissions, through the burning of fossil fuels, cement production and land use, have continued to track close to the high end of all scenario predictions24. Enhanced carbon uptake by the biosphere to date has served to slow the growth rate of atmospheric CO2 and our results support the hypothesis that net terrestrial CO2 uptake has been especially strong recently45. Without effective reduction of global CO2 emissions, however, future climate change remains a stark reality.
Methods
Global carbon cycle data
We used global carbon budget data from the Global Carbon Project1, in combination with diverse observational data sets from satellite remote sensing and distributed Earth observation networks, multiple prognostic DGVMs and a diagnostic modelling approach. The Global Carbon Project1 data set is a compilation of estimates of all major components of the global carbon budget, based on the combination of a range of data, algorithms, statistics and model estimates. This data set provided the long-term estimates of global emissions, along with estimates of the residual terrestrial sink from 10 DGVMs. Long-term atmospheric CO2 concentrations were provided by the National Oceanic and Atmospheric Administration’s (NOAA) Earth System Research Laboratory ( http://www.esrl.noaa.gov). Annual emissions of CO2 from the burning of fossil fuels, land use change and cement production from the Global Carbon Project1 were used in conjunction with the NOAA atmospheric CO2 concentration data to calculate the annual airborne fraction.
Diagnosing changes in the growth rate of atmospheric CO2
We used two methods to examine changes in the growth rate of atmospheric CO2 over time: a statistical linear model of the growth rate as a function of emissions, atmospheric CO2 concentrations and global CO2 sinks46. Rayner et al.46 showed that the growth rate can be modelled as a linear function of atmospheric CO2 concentration, and that deviations of the atmospheric growth rate from this linear model are an indication of changes in the sink strength of the biosphere. This is an informative approach as it incorporates the physical link between atmospheric CO2 concentrations and global CO2 sinks, thus allowing changes in that coupling to be studied. By examining the residuals of this linear model we identify a significant residual bias from 2002 to 2014, indicating a structural change in the relationship between atmospheric CO2 concentrations, emissions and global CO2 sinks (Supplementary Fig. 1). The second method, singular spectrum analysis (SSA), is used to extract the underlying temporal dynamics of both the growth rate and the airborne fraction.
Examining changes in atmospheric CO2 with linear modelling
The growth rate can be modelled as a linear function of atmospheric CO2 concentrations46. Deviations of the atmospheric growth rate from this linear model are an indication of changes in the sink strength of the biosphere. Such an approach is more informative than a simple linear model as a function of time, as it incorporates the physical link between atmospheric CO2 concentrations and global CO2 sinks, thus allowing changes in that coupling to be studied.
Formally, the global CO2 sink can be described as a linear function of CO2 concentration or, equivalently, CO2 mass. Thus, we write

where M is the mass of CO2 in the atmosphere and M0 is the background or equilibrium mass of CO2 in the atmosphere. Equation (1) can be simplified to

where B has units of per year and plays the role of an inverse residence time for excess carbon against the processes of land and ocean uptake.
Given that

where  is the growth rate of atmospheric CO2. We can substitute equation (2) into equation (3) to get
is the growth rate of atmospheric CO2. We can substitute equation (2) into equation (3) to get

Using observations of emissions from fossil fuel burning and land use change (Fanthro), along with the atmospheric CO2 concentrations and growth rate, it is possible to estimate B and F0 using standard statistical techniques.
The model thus constructed preserves the relationship between atmospheric CO2 concentrations, emissions and the growth rate of atmospheric CO2, on the basis of a proportional response of the global CO2 sinks. Any change in the strength of the global sinks can therefore be analysed by examining the residuals between the observed and predicted growth rate. We use the model, informed by the first 30 years of observations to test the hypothesis that the CO2 growth rate maintains the same linear relationship with atmospheric CO2 concentrations throughout. The residuals show a statistically significant deviation from being normally distributed around zero from 2002 (P<0.05, t-test, Supplementary Fig. 1). This shows that there is a pause in the growth rate of atmospheric CO2. Importantly, it also identifies changes in global CO2 sinks as the cause. We confirm this change in the growth rate by using SSA to extract the low frequency mode of variability corresponding to 5 years (see below).
Examining changes in atmospheric CO2 with SSA
SSA is a non-parametric spectral estimation method for extracting different modes of variability form a time series. The SSA method decomposes time series into a sum of components, each having a meaningful interpretation. Different modes of underlying variability can then be extracted by reconstructing the time series using only the eigenvalues relevant to the mode of variability in question. The name singular spectrum relates to the spectrum of eigenvalues in a singular value decomposition of a covariance matrix.
SSA first decomposes the time series into a set of empirical orthogonal functions and associated principal components in the spectral domain, following Takens’ embedding theorem47. Each component is dominated by a single oscillatory mode, and therefore has a simple representation in the frequency domain. This means that each empirical orthogonal function can thus be assigned a characteristic frequency. The functional separation from the decomposition step can be used to reconstruct the time series, either fully or only retaining specific modes of variability by using the relevant principal components. Thus, a time series can be finally described by a set of subsignals, Xf, each of which belongs to a well-defined frequency bin. All SSA analyses in this paper were performed using a 5-year frequency.
Despite of orthogonal base functions, extracted subsignals are subject to uncertainty due to a degree of inseparability of closely related modes of variability48. To quantify this uncertainty, we use a surrogate technique (the Iterative Amplitude Adjusted Fourier Transform49), following Mahecha et al.50 This approach generates a set of surrogates for each residual, corresponding to the extracted 5-year subsignal. The subsignal X5 is then re-extracted 100 times, giving an array of subsignal surrogates. The s.d. of the extracted subsignals quantifies the extraction uncertainty, and is shown in Fig. 1.
DGVMs of the terrestrial carbon cycle
DGVM output from two different model intercomparison projects was used in this analysis (Supplementary Table 1). As part of the Global Carbon Project1, transient runs from 10 DGVMs are available from 1959 to 2014 (www.globalcarbonproject.org/carbonbudget). These model simulations were assessed using observed atmospheric CO2 growth rates (Supplementary Fig. 2) and used to explore the decadal change in the land sink from 1959 to 2014 (Fig. 2). See Le Quere et al.1 for a detailed description of the models. We also use global simulations from 8 DGVMs (Supplementary Table 1) run as part of the Trends in Net Land-Atmosphere Exchange (TRENDY-v1) project (http://dgvm.ceh.ac.uk/node/9). In this project, common input forcing data were prescribed for a series of model experiments from 1901 to 2010. Here we use two model experiments from TRENDY-v1, varying either CO2 only (S1 (ref. 7): time-invariant climate; present-day land use mask) or climate only (S4 (ref. 51): time-invariant CO2; present-day land use mask). For more details on the TRENDY model simulations see Sitch et al.7
Satellite-based estimates of the terrestrial carbon cycle
In addition to the DGVMs, we used satellite-based estimates of ecosystem GPP combined with ecosystem respiration estimates from a diagnostic coupled PR model to quantify the likely effect of changes in global vegetation (through the fAPAR), and changes in water availability (though Alpha) on enhanced terrestrial uptake, from 1982 to 2013.
The diagnostic coupled PR model is based on a new light use efficiency (LUE) model of photosynthesis developed from first principles, and a semi-empirical model of ecosystem respiration developed based on eddy-covariance flux data.
The mechanistic photosynthesis model proposed by Farquhar et al.52 successfully captures the biochemical controls of leaf photosynthesis and responses to variations in temperature, light and CO2 concentration. According to the model, the gross photosynthesis rate, A, is limited by either the capacity of the Rubisco enzyme for the carboxylation of RuBP (ribulose-1,5-bisphosphate), or by the electron transport capacity for RuBP regeneration.
In the case of Rubisco limitation, the photosynthetic rate (Ac) is given by

where Vcmax is the maximum rate of Rubisco activity, ci is the intercellular concentration of CO2, Γ* is the CO2 compensation point in the absence of dark respiration and K is the Michaelis–Menten coefficient of Rubisco.
In the case of limitation by the electron transport capacity for RuBP regeneration, and assuming electron transport capacity is large (relative to Vcmax) such that the response of photosynthesis to light is linear under Rubisco limitation, the photosynthetic rate (Aj) is given by

where ϕ0 is the intrinsic quantum efficiency and I is the absorbed light.
The co-limitation or coordination hypothesis, which is strongly supported by empirical evidence53,54, predicts that photosynthesis under typical daytime field conditions is close to the point where Rubisco- and electron transport-limited photosynthesis rates are equal (that is, equation (5)=equation (6))55. In other words, the photosynthetic capacity of leaves adjusts to acclimate to the typical daytime light levels to be neither in sufficient excess to induce additional, non-productive maintenance respiration nor less than required for full exploitation of the available light. Recent empirical support comes from Maire et al.53, who tested the coordination hypothesis with 293 observations for 31 species grown under a range of environmental conditions, and found that average daily photosynthesis under field conditions is close to the point, where the Rubisco and electron transport photosynthesis rates are equal.
The coordination hypothesis allows for the prediction of photosynthesis through equation (6) using a LUE approach. Indeed the success of LUE models generally in predicting photosynthesis can be explained by the co-ordination hypothesis. Importantly, it also allows for the effect of CO2 on photosynthesis to be incorporated in such LUE models based on the first-principles understanding of the Farquhar et al.52 model.
By rewriting equation (6), substituting ci by the product of atmospheric CO2 (ca) and the ratio of leaf-internal to ambient CO2 (χ=ci/ca), GPP can be described as

where ϕ0 is the quantum yield and I is the absorbed light (here derived from satellite fAPAR).
Γ* depends on temperature, as estimated through a biochemical rate parameter (x) as described by Bernacchi et al.56:

here R is the molar gas constant (8.314 J mol−1 K−1) and x25=4.22 Pa is the photorespiratory point at 25 °C. ΔH is the activation energy for Γ* (37,830 J mol−1) and T is the temperature in K.
χ depends on air temperature and the vapour pressure deficit (VPD; D), and can be estimated following the least-cost hypothesis54. This states that an optimal long-term effective value of χ can be predicted as a result of plants minimizing their total carbon costs associated with photosynthetic carbon gain, and explicitly expressed with the following model

where D is VPD, K is the Michaelis–Menten coefficient of Rubisco and η* is the viscosity of water relative to its value at 25 °C. D is estimated as the difference between saturated and actual vapour pressure. Saturated vapour pressure (es) is estimated as the averaged saturated vapour pressure at maximum and minimum temperature with the Clausius–Clapeyron relationship, which is well approximated by

The Michaelis–Menten coefficient of Rubisco (K) in equation (9) is given by

where Kc and Ko are the Michaelis–Menten coefficient of Rubisco for carboxylation and oxygenation, respectively, expressed in partial pressure units, and Po is the partial pressure of O2. K responds to temperature via Kc and Ko, which is also described by equation (8) with specific parameters: ΔH is 79.43 kJ mol−1 for Kc and 36.38 kJ mol−1 for Ko, x25 is 39.97 Pa for Kc and 27,480 Pa for Ko. On the basis of equations (9)–(11), and assuming a typical value of χ25 as 0.8 (at T=298.15 K and D=1 kPa), parameter β of equation (9) is estimated as 356.51.
The GPP model implicitly assumes that nutrient limitations on GPP are manifest in allocation to foliage and are therefore contained in the observed fAPAR, as has been reported in recent empirical observations57,58. This is consistent with the theoretical expectation and empirical evidence that CO2-induced enhancement of biomass growth is possible even under nutrient-limited conditions59, and findings of increased below-ground allocation, including root exudation, on less fertile soils60.
Ecosystem respiration (Reco) in the diagnostic model is estimated via a photosynthesis-dependent respiration model61, which combines the joint influences of temperature, soil moisture and substrate availability on ecosystem respiration, and is designed for the diagnostic upscaling of Reco from observations at eddy-covariance towers to global scales. The model estimates monthly Reco as

where R0 is the reference respiration rate at the reference temperature Tref (15 °C), E0 is the activation energy and T0=−46.02 °C (ref. 61). k is the proportional contribution of GPP to ecosystem respiration through substrate availability at the reference temperature Tref, and is a measure of water availability, calculated as the ratio of actual to equilibrium evapotranspiration (see below). Conceptually, this model can be considered as the sum of a GPP-dependent term comprising autotrophic respiration and the fast-responding labile component of heterotrophic respiration, and a GPP-independent term standing for heterotrophic respiration of slower carbon pools. The two free model parameters (E0, k) were taken from the original study61, where 104 globally distributed sites from the FLUXNET network were used to derive plant functional type (PFT) specific parameters. Global PFT classifications were taken from the MODIS land cover product (MOD12, http://modis-land.gsfc.nasa.gov/landcover.html), curated at a resolution of 0.5° by the Global Land Cover Facility (http://glcf.umd.edu/data/lc/). For each 0.5° grid cell, we used the PFT that was most prevalent during the period 2000–2013. R0 was estimated for each 0.5° grid cell analytically, by solving the combined equations (7) and (12) for equilibrium net carbon uptake under preindustrial conditions.
Diagnostic model simulations performed
To examine the role of changes in each of the model drivers (air temperature, atmospheric CO2, radiation, moisture availability and vegetation cover) used in our analysis, we ran multiple global 0.5° simulations from 1900 to 2013 with the PR model. For each simulation, we removed the long-term trend in all drivers but one. This allowed us to quantify the direct first-order effect of long-term changes in each. An fAPAR climatology was used pre-1981.
Diagnostic model forcing data
Global monthly gridded weather data at 0.5° were provided by the Climate Research Unit at East Anglia University (CRU TS3.21)62. The total available photosynthetically active radiation, VPD and the ratio of actual to equilibrium evapotranspiration (α) were calculated from insolation and CRU climate data using a simple process-based bioclimatic model (STASH63). The GIMMS3G remotely sensed Normalized Difference Vegetation Index product64 provided monthly estimates of the fAPAR, an indicator of green vegetation cover, at 0.5°. Monthly fAPAR estimates are available from 1981 to the present.
Diagnostic model evaluation
We evaluated the efficacy of the PR model at multiple temporal and spatial scales. Evaluations performed include the following: a global comparison to interannual variability in the residual terrestrial sink from multiple DGVMs and estimates from the Global Carbon Project65 (Supplementary Fig. 2), site-level comparisons to time series of GPP and Reco from globally distributed individual sites in the La Thuile Fair Use FLUXNET data set (Supplementary Figs 5–8 and Supplementary Table 2); comparisons with the seasonal anomalies of GPP and Reco from 149 sites from the same data set (Supplementary Fig. 9); regional comparisons with seasonal changes in atmospheric CO2 concentrations from the NOAA global sampling stations (Supplementary Fig. 10); and a latitudinal comparisons to an empirical upscaling estimate of global GPP66 (Supplementary Fig. 11).
To compare PR model estimates of NEP to the observations at the NOAA stations, we used the TM2 atmospheric transport model67 to integrate and transport detrended monthly values of NEP for each 0.5° grid cell to the station locations. We then calculated both the modelled and observed CO2 seasonal cycle at the observation sites68.
Derivation of the sensitivity of GPP to CO2
GPP can be described as a function of atmospheric CO2 as

The sensitivity of GPP to ca can therefore be derived by taking the derivative of GPP with respect to ca, as

This requires the derivation of  , which can be formulated as:
, which can be formulated as:

It therefore follows that

Taking χ=0.8 and Γ*=43 p.p.m. (at 25 °C), the sensitivity of GPP is thus calculated as 37% at current levels of atmospheric CO2 (400 p.p.m.).
Examining the first derivative of the LUE model of GPP54,58 suggests a CO2 sensitivity (βCO2) of GPP of 37% at current atmospheric CO2 levels (400 p.p.m.), which is consistent with the observed response in FACE studies69. Our estimate of the change in GPP is also consistent with other process-based estimates7,8, but is larger than estimates from commonly used empirical upscaling techniques (Supplementary Fig. 12) as these do not account for the effect of increasing atmospheric CO2 on photosynthesis.
Long-term change in the sensitivity of GPP to changing ca
The change in the sensitivity of GPP to ca can also be derived analytically.
If we denote the sensitivity (from equation (16)) as

Then we can calculate the partial derivative of βCO2 as

And the partial derivative of gamma as

Combining equations (18) and (19) gives

The negative coefficient implies that the sensitivity of GPP to ca, βCO2, will decline with increasing ca. It is also clear from equation (20) that the response of βCO2 to ca is not linear, but decreases with ca. In other words, the magnitude of the sensitivity declination decreases with ca enhancement. Evaluating βCO2 at different atmospheric CO2 concentrations shows a decrease in βCO2 from 37% under current CO2 levels to 19% at double the current CO2 levels (Supplementary Table 3).
Data availability
Data used in this study are available from the Global Carbon Project data archive at the Carbon Dioxide Information Analysis Center (http://cdiac.ornl.gov/GCP/). This includes global carbon budget data and long-term simulations from DGVMs. Additional simulations used are available from the Trends in Net Land-Atmosphere Exchange (TRENDY) project (http://dgvm.ceh.ac.uk/node/9). All other data that support the findings of this study are available from the corresponding author on request.
Code availability
The code used in this study is available from the corresponding author on request.
Additional information
How to cite this article: Keenan, T. F. et al. Recent pause in the growth rate of atmospheric CO2 due to enhanced terrestrial carbon uptake. Nat. Commun. 7, 13428 doi: 10.1038/ncomms13428 (2016).
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Change history
14 July 2017
A correction has been published and is appended to both the HTML and PDF versions of this paper. The error has not been fixed in the paper.
References
Quéré, C. L. E. et al. Global Carbon Budget 2015. Earth Syst. Sci. Data 7, 349–396 (2015).
Raupach, M. R., Canadell, J. G. & Le Quéré, C. Anthropogenic and biophysical contributions to increasing atmospheric CO2 growth rate and airborne fraction. Biogeosciences 5, 1601–1613 (2008).
Bousquet, P. et al. Regional changes in carbon dioxide fluxes of land and oceans since 1980. Science 290, 1342–1347 (2000).
Cox, P. M. et al. Sensitivity of tropical carbon to climate change constrained by carbon dioxide variability. Nature 494, 341–344 (2013).
Ballantyne, A. P., Alden, C. B., Miller, J. B., Tans, P. P. & White, J. W. C. Increase in observed net carbon dioxide uptake by land and oceans during the past 50 years. Nature 488, 70–72 (2012).
Shevliakova, E. et al. Historical warming reduced due to enhanced land carbon uptake. Proc. Natl Acad. Sci. USA 110, 16730–16735 (2013).
Sitch, S. et al. Recent trends and drivers of regional sources and sinks of carbon dioxide. Biogeosciences 12, 653–679 (2015).
Schimel, D., Stephens, B. B. & Fisher, J. B. Effect of increasing CO2 on the terrestrial carbon cycle. Proc. Natl Acad. Sci. USA 112, 436–441 (2015).
Sarmiento, J. L. et al. Trends and regional distributions of land and ocean carbon sinks. Biogeosciences 7, 2351–2367 (2010).
Pan, Y. et al. A large and persistent carbon sink in the world’s forests. Science 333, 988–993 (2011).
Dai, A. Increasing drought under global warming in observations and models. Nat. Clim. Change 3, 52–58 (2012).
Westerling, A. L., Hidalgo, H. G., Cayan, D. R. & Swetnam, T. W. Warming and earlier spring increase western U.S. forest wildfire activity. Science 313, 940–943 (2006).
Kurz, W. A. et al. Mountain pine beetle and forest carbon feedback to climate change. Nature 452, 987–990 (2008).
Sheffield, J., Wood, E. F. & Roderick, M. L. Little change in global drought over the past 60 years. Nature 491, 435–438 (2012).
Brienen, R. J. W. et al. Long-term decline of the Amazon carbon sink. Nature 519, 344–348 (2015).
Zhou, L. et al. Widespread decline of Congo rainforest greenness in the past decade. Nature 509, 86–90 (2014).
Ma, Z. et al. Regional drought-induced reduction in the biomass carbon sink of Canada’s boreal forests. Proc. Natl Acad. Sci. USA 109, 2423–2427 (2012).
Anderegg, W. R. L., Kane, J. M. & Anderegg, L. D. L. Consequences of widespread tree mortality triggered by drought and temperature stress. Nat. Clim. Change 3, 30–36 (2012).
Ciais, P. et al. Europe-wide reduction in primary productivity caused by the heat and drought in 2003. Nature 437, 529–533 (2005).
Reichstein, M. et al. Climate extremes and the carbon cycle. Nature 500, 287–295 (2013).
Zhu, Z. et al. Greening of the Earth and its drivers. Nat. Clim. Change 6, 791–795 (2016).
Los, S. O. Analysis of trends in fused AVHRR and MODIS NDVI data for 1982-2006: Indication for a CO2 fertilization effect in global vegetation. Global Biogeochem. Cycles 27, 318–330 (2013).
Fyfe, J. C. et al. Making sense of the early-2000s warming slowdown. Nat. Clim. Change 6, 224–228 (2016).
Ciais, P. et al. in Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change eds Stocker T. F.et al. 465–570Cambridge Univ. Press (2013).
Karl, T. R. et al. Possible artifacts of data biases in the recent global surface warming hiatus. Science 348, 1469–1472 (2015).
Bahn, M. et al. Soil respiration in European grasslands in relation to climate and assimilate supply. Ecosystems 11, 1352–1367 (2008).
Moyano, F. E., Kutsch, W. L. & Schulze, E. D. Response of mycorrhizal, rhizosphere and soil basal respiration to temperature and photosynthesis in a barley field. Soil Biol. Biochem. 39, 843–853 (2007).
Högberg, P. et al. Large-scale forest girdling shows that current photosynthesis drives soil respiration. Nature 411, 789–792 (2001).
Jung, M. et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 467, 951–954 (2010).
de Jong, R., Verbesselt, J., Schaepman, M. E. & de Bruin, S. Trend changes in global greening and browning: Contribution of short-term trends to longer-term change. Glob. Chang. Biol 18, 642–655 (2012).
Milly, P. C. D. & Dunne, K. A. Potential evapotranspiration and continental drying. Nat. Clim. Change 6, 946–949 (2016).
Roderick, M. L., Sun, F., Lim, W. H. & Farquhar, G. D. A general framework for understanding the response of the water cycle to global warming over land and ocean. Hydrol. Earth Syst. Sci. 18, 1575–1589 (2014).
Schwalm, C. R. et al. Reduction in carbon uptake during turn of the century drought in western North America. Nat. Geosci. 5, 551–556 (2012).
Terrer, C., Vicca, S., Hungate, B. A., Phillips, R. P. & Prentice, I. C. Mycorrhizal association as a primary control of the CO2 fertilization effect. Science 353, 72–74 (2016).
Fatichi, S., Leuzinger, S. & Körner, C. Moving beyond photosynthesis: from carbon source to sink-driven vegetation modeling. New Phytol. 201, 1086–1095 (2014).
Betts, R. A., Jones, C. D., Knight, J. R., Keeling, R. F. & Kennedy, J. J. El Niño and a record CO2 rise. Nat. Clim. Change 6, 806–810 (2016).
Smith, S. J., Edmonds, J., Hartin, C. A., Mundra, A. & Calvin, K. Near-term acceleration in the rate of temperature change. Nat. Clim. Change 5, 333–336 (2015).
Quinn Thomas, R., Canham, C. D., Weathers, K. C. & Goodale, C. L. Increased tree carbon storage in response to nitrogen deposition in the US. Nat. Geosci. 3, 13–17 (2009).
Mercado, L. M. et al. Impact of changes in diffuse radiation on the global land carbon sink. Nature 458, 1014–1017 (2009).
Sitch, S., Cox, P. M., Collins, W. J. & Huntingford, C. Indirect radiative forcing of climate change through ozone effects on the land-carbon sink. Nature 448, 791–794 (2007).
Janssens, I. A. et al. Reduction of forest soil respiration in response to nitrogen deposition. Nat. Geosci. 3, 315–322 (2010).
Thornton, P. E., Lamarque, J. F., Rosenbloom, N. A. & Mahowald, N. M. Influence of carbon-nitrogen cycle coupling on land model response to CO2 fertilization and climate variability. Global Biogeochem. Cycles 21, 1–15 (2007).
Zaehle, S. & Friend, A. D. Carbon and nitrogen cycle dynamics in the O-CN land surface model: 1. Model description, site-scale evaluation, and sensitivity to parameter estimates. Global Biogeochem. Cycles 24, 1–13 (2010).
Yue, X., Keenan, T. F., Munger, W. & Unger, N. Limited effect of ozone reductions on the 20-year photosynthesis trend at Harvard forest. Glob. Chang. Biol. doi:10.1111/gcb.13300 (2016).
Francey, R. J. et al. Atmospheric verification of anthropogenic CO2 emission trends. Nat. Clim. Change 3, 520–524 (2013).
Rayner, P. J. et al. Recent changes in the global and regional carbon cycle: analysis of first-order diagnostics. Biogeosciences 12, 835–844 (2015).
Takens, F. in Dynamical Systems and Turbulence, Lecture Notes in Mathematics Vol. 898, 366–381Springer (1981).
Golyandina, N., Nekrutkin, V. & Zhigljavsky, A. Analysis of Time Series Structure: SSA and Related Techniques Chapman & Hall (2001).
Schreiber, T. & Schmitz, A. Surrogate time series. Phys. D 142, 346–382 (2000).
Mahecha, M. D. et al. Comparing observations and process-based simulations of biosphere-atmosphere exchanges on multiple timescales. J. Geophys. Res. 115, G02003 (2010).
Frank, D. C. et al. Water-use efficiency and transpiration across European forests during the Anthropocene. Nat. Clim. Change 5, 579–583 (2015).
Farquhar, G., von Caemmerer, S. & Berry, J. A biochemical model of photosynthetic CO2 assimilation in leaves of C 3 species. Planta 90, 78–90 (1980).
Maire, V. et al. The coordination of leaf photosynthesis links C and N fluxes in C3 plant species. PLoS ONE 7, 1–15 (2012).
Prentice, I. C., Dong, N., Gleason, S. M., Maire, V. & Wright, I. J. Balancing the costs of carbon gain and water transport: testing a new theoretical framework for plant functional ecology. Ecol. Lett. 17, 82–91 (2014).
Haxeltine, A. & Prentice, I. C. A general model for the light-use efficiency of primary production. Funct. Ecol. 10, 551–561 (1996).
Bernacchi, C. J., Singsaas, E. L., Pimentel, C., Portis, A. R. Jr & Long, S. P. Improved temperature response functions for models of Rubisco-limited photosynthesis. Plant Cell Environ. 24, 253–259 (2001).
Vicca, S. et al. Fertile forests produce biomass more efficiently. Ecol. Lett. 15, 520–526 (2012).
Wang, H., Prentice, I. C. & Davis, T. W. Biophsyical constraints on gross primary production by the terrestrial biosphere. Biogeosciences 11, 5987–6001 (2014).
Dybzinski, R., Farrior, C. E. & Pacala, S. W. Increased forest carbon storage with increased atmospheric CO2 despite nitrogen limitation: a game-theoretic allocation model for trees in competition for nitrogen and light. Glob. Chang. Biol. 21, 1182–1196 (2015).
Aoki, M., Fujii, K. & Kitayama, K. Environmental control of root exudation of low-molecular weight organic acids in Tropical Rainforests. Ecosystems 15, 1194–1203 (2012).
Migliavacca, M. et al. Semiempirical modeling of abiotic and biotic factors controlling ecosystem respiration across eddy covariance sites. Glob. Chang. Biol. 17, 390–409 (2011).
Harris, I., Jones, P. D., Osborn, T. J. & Lister, D. H. Updated high-resolution grids of monthly climatic observations—the CRU TS3.10 Dataset. Int. J. Climatol. 34, 623–642 (2014).
Gallego-Sala, A. et al. Bioclimatic envelope model of climate change impacts on blanket peatland distribution in Great Britain. Clim. Res. 45, 151–162 (2010).
Zhu, Z. et al. Global data sets of vegetation leaf area index (LAI)3g and fraction of photosynthetically active radiation (FPAR)3g derived from global inventory modeling and mapping studies (GIMMS) normalized difference vegetation index (NDVI3G) for the period 1981 to 2. Remote Sens. 5, 927–948 (2013).
Le Quéré, C. et al. Global carbon budget 2014. Earth Syst. Sci. Data 7, 47–85 (2015).
Jung, M. et al. Global patterns of land-atmosphere fluxes of carbon dioxide, latent heat, and sensible heat derived from eddy covariance, satellite, and meteorological observations. J. Geophys. Res. 116, 1–16 (2011).
Kaminski, T., Heimann, M. & Giering, R. A coarse grid three-dimensional global inverse model of the atmospheric transport: 1. Adjoint model and Jacobian matrix. J. Geophys. Res. 104, 18535 (1999).
Knorr, W. & Heimann, M. Impact of drought stress and other factors on seasonal land biosphere CO2 exchange studied through an atmospheric tracer transport model. Tellus B 47, 471–489 (1995).
Norby, R. J. & Zak, D. R. Ecological lessons from free-air CO2 enrichment (FACE) experiments. Annu. Rev. Ecol. Evol. Syst. 42, 181–203 (2011).
Acknowledgements
T.F.K. acknowledges support from the Laboratory Directed Research and Development Program of Lawrence Berkeley National Laboratory under U.S. Department of Energy Contract No. DE-AC02-05CH11231, and a Macquarie University Research Fellowship. This research contributes to the AXA Chair Programme in Biosphere and Climate Impacts and the Imperial College initiative on Grand Challenges in Ecosystems and the Environment. J.G.C. thanks the support from the Australian Climate Change Science Program. Eddy covariance data used was acquired by the FLUXNET community and in particular by the following networks: AmeriFlux (U.S. Department of Energy, Biological and Environmental Research, Terrestrial Carbon Program (DE-FG02-04ER63917 and DE-FG02-04ER63911, DE-SC0006708)), CarboEuropeIP, Fluxnet-Canada (supported by CFCAS, NSERC, BIOCAP, Environment Canada and NRCan). We acknowledge the financial support to the eddy covariance data harmonization provided by CarboEuropeIP, FAO-GTOS-TCO, iLEAPS, Max Planck Institute for Biogeochemistry, National Science Foundation, University of Tuscia, Université Laval and Environment Canada and US Department of Energy and the database development and technical support from Lawrence Berkeley National Laboratory, Berkeley Water Center, Microsoft Research eScience, Oak Ridge National Laboratory, University of California—Berkeley, University of Virginia. We thank Ranga Myneni and Zaichun Zhu for the provision of the fAPAR data set, the Max Planck Institute for Biogeochemistry Department of Biogeochemical Integration for the provision of the upscaled GPP data and Miguel Mahecha for advice on the S.S.A. We thank the TRENDY team, Stephen Sitch, Pierre Friedlingstein, Chris Huntingford, Ben Poulter, Anders Ahlström, Mark Lomas, Peter Levy, Sam Levis, Sönke Zaehle, Nicolas Viovy, Ning Zeng and Phillipe Peylin for the provision of the DGVM simulations, and the researchers of the Global Carbon Project for making their data available.
Author information
Authors and Affiliations
Contributions
T.F.K. and I.C.P. designed the study and are responsible for the integrity of the manuscript; T.F.K. compiled the data sets, and detailed and performed the analysis, with input from all other authors; T.F.K. wrote the manuscript. All authors discussed and commented on the results and the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-12 and Supplementary Tables 1-3 Supplementary References. (PDF 4878 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Keenan, T., Prentice, I., Canadell, J. et al. Recent pause in the growth rate of atmospheric CO2 due to enhanced terrestrial carbon uptake. Nat Commun 7, 13428 (2016). https://doi.org/10.1038/ncomms13428
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms13428
This article is cited by
-
Elevational patterns of warming effects on plant community and topsoil properties: focus on subalpine meadows ecosystem
Journal of Mountain Science (2024)
-
Evidence and attribution of the enhanced land carbon sink
Nature Reviews Earth & Environment (2023)
-
Surprising stability of recent global carbon cycling enables improved fossil fuel emission verification
Nature Climate Change (2023)
-
On the evidence of a trend in the CO2 airborne fraction
Nature (2023)
-
Boreal conifers maintain carbon uptake with warming despite failure to track optimal temperatures
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.