Abstract
Storage of anthropogenic CO2 in geological formations relies on a caprock as the primary seal preventing buoyant super-critical CO2 escaping. Although natural CO2 reservoirs demonstrate that CO2 may be stored safely for millions of years, uncertainty remains in predicting how caprocks will react with CO2-bearing brines. This uncertainty poses a significant challenge to the risk assessment of geological carbon storage. Here we describe mineral reaction fronts in a CO2 reservoir-caprock system exposed to CO2 over a timescale comparable with that needed for geological carbon storage. The propagation of the reaction front is retarded by redox-sensitive mineral dissolution reactions and carbonate precipitation, which reduces its penetration into the caprock to ∼7 cm in ∼105 years. This distance is an order-of-magnitude smaller than previous predictions. The results attest to the significance of transport-limited reactions to the long-term integrity of sealing behaviour in caprocks exposed to CO2.
Similar content being viewed by others
Introduction
Carbon capture and storage will form an essential part of the technologies needed to reduce anthropogenic CO2 emissions if costly climate change is to be avoided1. CO2, separated at power stations and industrial plants, is compressed and injected into saline geological reservoirs as a supercritical fluid2. The CO2 is less dense than the saline brines at typical formation temperatures, driving buoyant migration, and will need to be retained by impermeable caprocks as the primary mechanism for ensuring effective storage. Subsidiary processes including dissolution of CO2 in formation brines, trapping of CO2 by capillary forces and precipitation of carbonate minerals will aid storage security over the 104 year timescales needed to avoid climate impacts3, but operation of these processes is dependent on the initial retention under the caprock. The caprocks in sedimentary successions suitable for CO2 storage will most commonly comprise clay-rich mudstones or shales that act as barriers to CO2 migration by two mechanisms4. Their low permeabilities (<10−19 m2) restrict fluid fluxes to very low rates. Further, capillary entry pressures for CO2 of 0.5–5 MPa4 will restrict penetration of CO2, allowing transport of CO2 only by sluggish diffusion in the brine phase, which will be further retarded by the complex geometry of the pore networks. The addition of CO2 forms acid brines that react with clay-rich caprocks to drive dissolution and precipitation of minerals5,6,7, with consequences for the evolution of porosity and the geomechanical integrity of the seals8, within regions penetrated by the diffusing CO2. The initial dissolution of rapidly reacting carbonate and oxy-hydroxide phases will buffer the pH of CO2-saturated brines to ∼5 followed by the more sluggish dissolution of silicate and phyllosilicate minerals, which further increase pH and cause re-precipitation of carbonate phases5,9,10. However, it is uncertain as to whether these fluid–rock reactions may lead to mineral precipitation-induced self-sealing phenomena that limit the pervasion of the CO2, as predicted by some numerical simulations5,9,10,11,12,13, or self-enhancing mineral dissolution and porosity generation, which generate a continuous increase in caprock transport properties, as observed in some laboratory experiments14,15,16,17. Direct observations of caprock materials exposed to CO2 over the timescales requisite for storage are critical to address this uncertainty, where the coupled reactive-transport phenomena are integrated over the appropriate temporal and spatial scales.
Fundamental uncertainties in the prediction of coupled reactive transport in low permeability clay-rich caprocks include a poor understanding of the relationship between reaction-induced changes in porosity and the pore-network structure, and the consequences for the rates of solute transport18, the uncertain mineral surface areas and kinetics of the mineral reactions in natural settings19, the rates of which may be limited by the intrinsic surface reaction rates of the minerals or by rates of solute transport20, and the reaction pathways in natural settings, including the role of acid redox reactions as a CO2 sink21, which will retard the rates of diffusive CO2 transport.
We address this fundamental gap in our knowledge of the long-term impacts of CO2-charged fluids on caprock integrity by examining caprock recovered from a natural CO2 reservoir. Although this reservoir is at much shallower depths and lower pressures than needed for geological carbon storage, the reactions between minerals and CO2-saturated brines are little affected by pressure. Mineralogical and petrophysical measurements are used to assess the impacts of CO2-promoted reactions on the caprock pore-network transport properties. The measurements reveal that the CO2-charged mildly reducing brines only removed haematite from the basal 7 cm of the haematite-bearing claystone cap rock. This data is used to constrain analytical and numerical reaction–diffusion models, which confirm that the fluid–rock reactions retard CO2 transport by an order of magnitude, and that the timescale of alteration is ∼105 years, comparable with geochronological constraints on the duration of CO2 storage in the reservoir. The small but transient increases in porosity generated by the mineral reactions do not significantly enhance reaction front velocities. The results attest to the significance of transport-limited reactions to the long-term integrity of sealing behaviour in caprocks exposed to CO2.
Results
Mineral reactions and petrophysical changes in the caprock
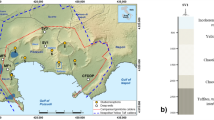
Core and fluid samples were collected from a sequence of CO2-charged reservoirs and intervening caprocks during scientific drilling within the footwall of the Little Grand Wash Fault, Green River, Utah22 (Fig. 1). The 325-m deep drillhole transected reservoirs of CO2-charged brine in the Middle Jurassic Entrada and Lower Jurassic Navajo Sandstone, and the intervening Middle Jurassic Carmel Formation caprock. The geochemistry of fluid samples, collected at formation pressures through the Navajo Sandstone reservoir, tracks contemporary filling via artesian flow of CO2 and CO2-saturated brines through the faults23. The reservoir fluids are mixtures of Na-Cl-SO4 brine and meteoric groundwater with low pH (5.1–5.3), reducing (0 to −50 mV), SO4-rich and contain trace quantities of H2S and CH4. The migrating CO2 and CO2-saturated brine are thought to originate from an accumulation of supercritical CO2 within Carboniferous strata at depth24. U-Th geochronology of carbonate veining in associated faults attests to CO2 out-gassing regionally for ca. 400 ka and locally for at least 114 ka, providing an independent constraint of the duration over which the Carmel Formation caprock has been exposed to CO2-charged brines25. Cycles in the chemistry of the fault-hosted carbonate veins have been attributed to cyclic charging of the shallow reservoirs with multiple pulses of CO2-rich fluids, which coincide with periods of crustal unloading during regional deglaciations26.
The hole was drilled 90 m north of the Little Grand Wash Fault south of Green River, Utah22,23. It transected the Entrada Formation, the Carmel Formation, a small splay fault related to the Little Grand Wash fault within the Carmel Formation, and entered the Navajo Formation at a depth from surface of 200.11 m. Dissolved CO2 and salinity gradients within fluids sampled from the Navajo Formation indicate that CO2-saturated brines (shaded) migrate (wavy lines) from the fault zones along the base of the aquifers and mix with meteoric groundwaters23. Horizons with similar CO2-charged fluids were encountered in the Entrada and Carmel Formations.
The Carmel Formation constitutes a regional seal between the Navajo and Entrada aquifers. It comprises a 50-m-thick complex package consisting of three major lithofacies; interbedded, unfossiliferous red and grey shale and bedded gypsum, red and grey claystone/siltstone and fine-grained sandstone23. These are interpreted as marine sediments deposited in quiet, subtidal conditions under the influence of periodic hypersaline water27.
In the Green River drill hole, a basal 16-cm-thick claystone of the Carmel Formation acts as a caprock to the CO2-rich brines in the underlying Navajo Sandstone. This claystone was subsampled at ∼4 mm vertical resolution and analysed for quantitative mineralogy, carbonate δ18O and δ13C isotopic compositions, 87Sr/86Sr ratios, bulk mineral surface area and porosity (Fig. 2a, Methods, Supplementary Fig. 1 and Supplementary Tables 1–3).
(a) Haematite (vol-%) profiles across the basal Carmel claystone. Solid curve is least-squares best fit to haematite vol-% profile to equation (6) adjusting ϕs, q and l (best fit values and 1σ uncertainties given on figure) with 1σ uncertainty on haematite of 7% relative, but a minimum uncertainty of 0.1 volume %. Dashed line shows profile for q=37 m−1 taken as lower limit as discussed in text. It is noteworthy that the upper 1 cm of the claystone is bleached adjacent to a CO2-bearing sandstone within the Carmel Formation. (b) Porosity calculated from SANS/VSANS measurements across caprock. (c) Tortuosity, τ2, (left-hand axis) and diffusivity De, (right-hand axis) calculated from SANS/VSANS measurements across caprock (see Methods).
The primary mineralogy of the unaltered portion of the red claystone comprises illite, quartz, dolomite, K-feldspar and haematite (Supplementary Fig. 2), with >50% clay-sized particles. This basal claystone is typical of oxidized redbed shallow marine and continental mudstones, forming a representative analogue to other important reservoir seals such as the North Sea Mercia Mudstone28 and the Formations in the Triassic Keuper29.
The basal 7 cm of the originally red claystone, at the caprock-reservoir interface, is distinctively bleached white–yellow, reflecting quantitative removal of haematite (Fig. 2a), with loss of the primary dolomite and precipitation of ankerite–dolomite, sulphide minerals and gypsum (Fig. 2a and Supplementary Fig. 1A). Carbonate, sulphate, sulphide and clay mineral compositions have been analysed using Electron microprobe analyses (EMPA; Methods and Supplementary Table 4). Large-scale bleaching of exhumed redbed sandstones and siltstones in the Green River location has previously been related to flow of reducing CO2-bearing fluids30,31,32. A comparable basal unit from the Carmel Formation from a drill hole free from CO2 33 km north west (NW) of Green River shows no discernible change in mineralogy or O- and C-isotope ratios as a result of reactions at the base of the caprock (Supplementary Fig. 3).
The observed petrological changes are consistent with a series of interdependent reactions involving CO2- and H2S-promoting dissolution of haematite following the stoichiometry

Dolomite dissolution was coupled with the growth of ankerite–dolomite, with Fe2+ derived from the acid-reductive dissolution of haematite (Fig. 2a and Supplementary Fig. 2A,B), accompanied by shifts in the O-, C- and Sr-isotopic composition of the newly precipitated ankerite–dolomite cements (Supplementary Fig. 1B–D). Pyrite precipitated upstream and euhedral haematite, chalcopyrite and covellite precipitated downstream of the haematite dissolution front, with Fe and Cu supplied from primary haematite dissolution and sulphide supplied from the invading fluid (Supplementary Fig. 2B–D). The K-feldspar dissolution close to the reservoir caprock interface led to the precipitation of pore-filling illite (Supplementary Fig. 2E,F).
Pore network structures at 4 mm intervals along the reaction profile were characterized using N2-BET and small and very small angle neutron scattering techniques ((V)SANS; see Methods). The porosity profile shows a remarkable increase in porosity directly upstream of the haematite dissolution front, but further upstream precipitation of ankerite–dolomite, pyrite, gypsum and illite cause a progressive decrease in porosity to values below that of unreacted caprock (Fig. 2b and Supplementary Table 3).
The tortuosity (τ2) of the pore network at each sample point in the profile (Fig. 2c) was calculated from the surface and volume fractal dimensions of the pore structure, measured by the (V)SANS data (Supplementary Fig. 5 and Methods). This allows the calculation of the effective diffusivity of a species, De (m2 s−1) in the tortuous pore network, which is related to the diffusion coefficient in water, Dw, and the diffusion accessible porosity, ϕ, by

The molecular diffusivity of CO2 and H2S in water at 20 °C is ∼2 × 10−9 m2 s−1 (ref. 33). The calculated porosities, surface fractal dimensions, Ds, and pore volume fractal values, Dv, (Supplementary Table 3) imply a τ2 of ∼37 and effective diffusivities for CO2 and H2S of 5 × 10−12 m2 s−1 in the unaltered portions of the caprock (Fig. 2c). The calculated porosities agree well with the porosity distribution measured by N2-BET over the same size range for sample NPS-069 (Supplementary Fig. 6). Clarkson et al.34 and Bertier et al.35 discuss comparison of porosities calculated from (V)SANS data with N2 physiosorption data for comparable shales and emphasize the limitations of the physiosorption data. The calculated diffusivities are at the lower limits of experimentally determined measurements for tortuosity and CO2 effective diffusivities in shales18,36,37,38, and are consistent with the relative high clay content of these samples. It should be noted that our calculations assume that the porosity is interconnected for pores over the length scales sampled (1.2–1,500 nm).
In the altered portion of the caprock the estimated tortuosity decreases to 7 and effective diffusivities increase to 3 × 10−11 m2 s−1, because pore connectivity increases and the roughness of the pore–solid interface decreases due to mineral dissolution (Fig. 2c). The diffusivities decrease to 1.9 × 10−11 m2 s−1 further upstream following mineral reprecipitation, but the tortuosity of the pore network does not significantly increase, suggesting that there is a non-recoverable impact of mineral dissolution on rock transport properties.
Modelling reactive transport in the caprock
The mineralogical profiles record the propagation of mineral–fluid reaction fronts within the caprock lithology, driven by the upward diffusion of CO2 and H2S. Modelling of the reactive transport enables examination of the key processes governing the reactive diffusion of CO2 including the timescale and the ratio of transport rates to mineral reaction rates. Upward advective transport by fluids must be negligible given the low permeability of the unreacted caprock of ∼10−22 m2 (Methods), which equates to a hydraulic conductivity of ∼10−15 m s−1, and thus a Péclet number of ∼10−3 m, over the length scale of the alteration. An analytical solution to one-component diffusive transport with mineral dissolution rate described by linear kinetics39 captures the important physics and informs the essential approximations necessary for reactive transport modelling with multiple components. On initiation of diffusion, the reactant mineral volume fraction decreases until the phase is exhausted at the base of the caprock. From this time, τ0, a reaction front migrates downstream away from the base, where τ0 is given by,

where kf (m s−1) is mineral reaction rate, α (m2 m−3) is the mineral surface area, Vs is the mineral molar volume (m3 mol−1) and  is the volume fraction of the reactant mineral phase initially present. ΔC0=Ceq−C0 where Ceq is the solute concentration (mol m−3) in equilibrium with the reactant mineral phase and C0 is the solute concentration in the infiltrating fluid (for full derivation of equations after ref. 39, see Methods), which can be modelled in terms of consumption of CO2, H2S or Fe2O3, for which the solutions are identical and fixed by the stoichiometry of reaction (1). The position of the reaction front, l (m) at time t (s) is given by solution of
is the volume fraction of the reactant mineral phase initially present. ΔC0=Ceq−C0 where Ceq is the solute concentration (mol m−3) in equilibrium with the reactant mineral phase and C0 is the solute concentration in the infiltrating fluid (for full derivation of equations after ref. 39, see Methods), which can be modelled in terms of consumption of CO2, H2S or Fe2O3, for which the solutions are identical and fixed by the stoichiometry of reaction (1). The position of the reaction front, l (m) at time t (s) is given by solution of

where q (m−1) is given by

where De is the effective diffusion coefficient defined in equation (2). At t>τ0, the variation of reactant mineral volume with time and distance (x, m) downstream of the reaction front is given by

In the absence of advection, solutions for the position and velocity of the reaction front (equation 4) are divided into two regimes and the broadening of the front depends dominantly on the kinetics of the reaction40. If ql>1 (that is, the Damköhler number (ql)2 is large), reaction rates are fast compared with diffusion rates and the propagation rate depends on the diffusivity of the species driving the reaction and the reaction stoichiometry. For ql<1, the position of the reaction front is a linear function of time and the velocity of the front depends on the reaction rate constant and mineral surface area. Figure 3 illustrates such solutions, calculated for transport of Fe in the fluid phase, for time, t, as a function of haematite dissolution rate, kR (mol m−2 s−1) given the reaction stoichiometry of equation (1) and contoured for the effective diffusivity of the caprock, De, estimated from pore volume and fractal pore network modelling of SANS data.
The duration of caprock alteration calculated from equation (4) given the time for the reaction front to develop (τ0; equation (3)) and the displacement distance of the front, l. Calculations are performed on the basis of Fe in equation (1). Shaded area denotes solutions for 37<q<228 m−1, which gives a haematite dissolution rate, kR, between 1 × 10−10 and 5 × 10−9 mol m−2 s−1 from equation (5) for a diffusion coefficient of 5 × 10−12 m2 s−1. Solid line shows median solution with De=5 × 10−12 m2 s−1 and ΔC0=2.9 mol m−3. Dashed lines show extreme solutions with the minimum estimate of diffusivity of 10−12 m2 s−1 and minimum ΔC0 of 1.9 mol m−3 giving maximum reaction times and a high estimate of diffusivity of 1 × 10−11 m2 s−1, combined with a maximum estimate of ΔC0 of 3.95 mol m−3 giving minimum reaction times. Uncertainties in the duration of caprock alteration propagated from the other variables are small compared with those from the potential range of caprock diffusivities and reaction stoichiometry.
The haematite mode profile (Fig. 2a) primarily reflects dissolution described by equation (1), but potentially with additional precipitation of haematite downstream of the reaction front as a result of multicomponent transport (Fig. 2a and c.f. ref. 30). The geometry of the mineral dissolution front, characterized by the spatial variation in haematite modes, is described by equation (6). The curvature of this profile, for an assumed constant effective diffusivity at and upstream of the dissolution front, depends only on the kinetics of the reaction. A least-squares best fit gives a value for the exponential constant q in equation (4) of 228±31 m−1 (1σ). If the profile is augmented by haematite precipitation, q might be as small as ∼37 m−1. Given that l=0.07 m (Fig. 2a), ql is >2 and reaction rates are fast compared with diffusive transport. For De=5 × 10−12 m2 s−1 (Fig. 2c), the reaction stoichiometry of equation (1), a haematite-specific surface area calculated from a volume-weighted total SANS surface area and inlet fluid compositions from downhole sampling23 (Methods), these values of q imply a timescale between 3,000 and 10,000 years, and haematite dissolution rates in the range 1 × 10−10 to 5 × 10−9 m2 s−1 (Fig. 3). The latter compare well with laboratory estimates for haematite dissolution rates under acidic conditions in the presence of low concentrations of dissolved H2S41 (Methods).
The modelling above only considers transport of Fe2O3 and dissolution of haematite as the major component buffering fluid pH and oxidation state. The mineralogical profiles (Fig. 2a and Supplementary Fig. 1A) show that dissolution/precipitation of dolomite, ankerite–dolomite, sulphate, sulphide, K-feldspar and illite also occur. The reactive diffusion was modelled with multiple components and phases by numerical simulation using PHREEQC42 (Fig. 4, Methods). A 15-cm-long one-dimensional reactive–diffusive model comprising 30 cells of 5 mm length was constructed. Each cell initially contained the mineral volumes measured by X-ray diffraction (XRD) and porosity measured by (V)SANS in unreacted portions of the caprock. The fluid chemistry occupying the boundary reservoir cell was based on analyses of the modern reservoir fluids43 with a redox state defined using the SO42−/H2S redox couple (sample DFS00413 with SO4 20.7 mmol and H2S 0.5 mmol). The initial caprock pore fluid chemistry was calculated similar to that in equilibrium with the caprock mineralogy (reactive minerals haematite, Mg-dolomite, K-feldspar and illite), with pCO2, pO2 and salinity typical of Jurassic marine shales43 (Supplementary Table 4). Models were run assuming local fluid–mineral equilibrium and pyrite, an Fe-bearing dolomite (Mg0.9Fe0.1CaCO3), and illite were allowed to precipitate (Supplementary Table 2). A De value of 5 × 10−12 m2 s−1 was used for all aqueous species. The model timescale was 125,000 years, with a time step of 7 days required to reach convergence of the numerical solution.
(a) PHREEQC42 model run for 125,000 years for constant CO2 at saturation on basal boundary. A 15 cm-long one-dimensional reactive–diffusive model comprising 30 cells of 5 mm length was used with initial mineralogy (mol l−1) calculated from XRD analyses, pore volumes from SANS of the unaltered portion of the caprock, the invading pore fluid chemistry based on the reservoir fluids (Supplementary Table 4) and the initial caprock pore fluid chemistry was taken to be a fluid in equilibrium with the caprock mineralogy, with pCO2, pO2 and salinity estimates for typical Jurassic marine shales. The initial redox state of the invading fluid was defined using the SO4 2−/H2S redox couple. Models were run assuming local fluid–mineral equilibrium and a constant De value of 5 × 10−12 m2 s−1 was used for all aqueous species. The model timescale was 125,000 years with a time step of 7 days. (b) One-dimensional model with the same starting conditions as a but with two 25,000 year phases of CO2-saturated brine in the basal cell with an intervening 75,000 year period where the basal cell contained a CO2-poor brine. The results of the two episodes of CO2 saturation are seen as double peaks in pyrite and dolomite modes as the CO2 from each pulse diffuses into and reacts with the caprock.
The models reproduce the key observations (Fig. 4a). The haematite dissolution front migrates ∼7 cm in >104 years. Dolomite dissolves downstream of the front and Fe-dolomite is precipitated upstream of the reaction front (Supplementary Fig. 2B). Pyrite is precipitated initially close to the caprock-reservoir contact and migrates very slowly. K-feldspar dissolves only at the inlet, driving local precipitation of illite. The additional complexities observed with multiple zones of pyrite precipitation probably result from the episodic release of CO2-charged brines by the fault system26. Models run with two episodes of CO2 injection reproduce a similar pattern in which the diffusion of mineral profiles into the caprock preserves a record of the evolution of reservoir fluid compositions (Fig. 4b) apparent as double peaks in pyrite and dolomite.
Discussion
This study provides evidence for the slow penetration rate of CO2-promoted fluid–rock reactions into clay-rich caprocks and the development of a stable reaction front without a significant positive feedback loop between porosity enhancement and the velocity of the front. SANS methods are effective at resolving micrometre-scale changes in pore network characteristics and diffusive transport properties, with the magnitude of the change of the latter being approximately half an order of magnitude. This provides evidence to refute observations from laboratory experiments, which posit a significant increase in the transport properties of caprocks following exposure to CO2-charged brines14, and CO2-charged brines and H2S17. Multicomponent numerical modelling of the reactive–diffusive transport reproduced the major mineralogical changes accompanying diffusion of the CO2, although detailed variations reflect the complex heterogeneity of natural rocks, and the cyclic variation in CO2 charging of the underlying reservoir. The important conclusion from the analytical and numerical modelling is that the timescale for the development of the 7-cm reaction front is ∼10,000 to 100,000 years, consistent with the geological evidence for the duration of the CO2 supply to the Little Grand Fault system25. Previous numerical models of reactive–diffusive transport of CO2 in clay-rich caprocks, unconstrained by observations from natural systems, have predicted the development of mineral alteration profiles over length scales of metres on a 10,000 year timescale5,9,10,12. In addition, these modelling studies did not consider redox reactions, which as demonstrated here, are an important sink for CO2 invading the caprock and contribute significantly to retardation of the CO2-diffusive transport. The results demonstrate that numerical models of reactive transport in low-diffusivity media, where mineral reaction kinetics do not limit reaction rates, successfully predict reactions and reaction rates, providing the full chemical complexity is modelled. The results also show that the mineralogy of caprocks and chemistry of potential CO2-charged brines will need to be considered on a case-by-case basis.
Fluid–rock reaction has substantially retarded diffusive transport of the CO2, which would have penetrated ∼8 m in 100,000 years in the absence of reaction, based on a diffusion coefficient of 5 × 10−12 m2 s−1. Rock-buffering reactions are effective at establishing fluid–mineral equilibrium over centimetre length scales. In this caprock, CO2-charged fluid–mineral reactions act to enhance caprock integrity over a time period comparable to that needed for effective geological carbon storage.
Methods
Drill core processing
HQ core (63.5 mm diameter) samples of the caprock interval, recovered from well CO2W55 near the town of Green River, Utah, were slabbed and then sliced parallel to bedding at ∼3–5 mm resolution, using a steel blade rock saw. Approximately 2–5 g of air-dried sample was powdered to ≤100 μm size in a ball mill using an agate container and balls, and subsamples were taken for individual analyses. Samples for XRD measurements were crushed and milled separately. A comparative sample profile from the base of the Carmel Formation, in a region where CO2 is absent, was collected from sections of core BH2 recovered during drilling of the Bighole fault44, located ∼35 km north east (NE) of Green River. This comparison profile was prepared and analysed for quantitative mineralogy and carbonate O- and C-isotopes using the same methods as for the CO2W55 core interval (Supplementary Fig. 3).
XRD measurements
XRD measurements to determine mineralogy (Supplementary Table 1) have been performed at RWTH Aachen University as stated in ref. 45, except the counting time is 20 s for each step of 0.02° 2θ recorded from 2° to 92° 2θ. Rock samples are crushed manually in a mortar with care taken to avoid strain damage and crushed material together with an internal standard (Corundum, 20 wt%) is milled in ethanol with a McCrone Micronising mill (15 min). Quantitative phase analysis is performed by Rietveld refinement using BGMN software, with customized clay mineral structure models46. The precision of these measurements, from repetitions, is better than 0.1 wt% for phases of which the content is above 2%. The accuracy cannot be determined because of the lack of pure clay mineral standards, but is estimated to be better than 10% (relative). Mineral compositions relate to the crystalline content of the analysed samples.
Stable isotopes
Carbonate mineral δ13C and δ18O were determined at the University of Cambridge on duplicate subsamples of 300–500 μg using a Thermo Gas Bench attached to a Thermo MAT 253 mass spectrometer in continuous flow mode, with an analytical precision of ±0.12‰ and ±0.20‰, respectively, (2σ). δ13C and δ18O results are reported, relative to the VPDP and VSMOW standards, as averages of these duplicate analyses, with error bars that are the 2σ s.e. of duplicate averages (Supplementary Table 2 and Supplementary Fig. 1).
Sr-isotopes
87Sr/86Sr of rock leachates and residues were determined at the University of Cambridge following ref. 47 (Supplementary Table 2 and Supplementary Fig. 1). The internal standard NBS 987 gave 0.710263±0.000009 (1σ) on 158 separate measurements made during the course of these analyses. Strontium blanks were always <250 pg and negligible for the Sr concentration of these samples.
EMPA and scanning electron microscopy analyses
EMPA of mineral compositions were determined using a Cameca SX-100 electron microprobe, using energy-dispersive spectrometry at the University of Cambridge (15 kV, 10 nA; beam diameter 5 μm) with fayalite, rutile, corundum, periclase and pure Co, Ni, Mn, Cr, Zn and Cu standards (Supplementary Table 4). Spectra were collected with a PGT prism 2,000 ED detector and the data reduced with the PGT excalibur software. Back-scatter electron and secondary electron images were obtained using the JEOL 820 scanning electron microscope in the Department of Earth Sciences, University of Cambridge, with an accelerating voltage of 20 kV and 1 nA beam current.
Porosity measurements by N2 physisorption
The surface area and pore-size distribution of sample NPS-069 was investigated using nitrogen gas adsorption techniques at RWTH Aachen University as stated in ref. 35 (Supplementary Table 3 and Supplementary Fig. 6). Specific surface area and total pore volume were determined from nitrogen gas adsorption at 77.3 K, by means of the static-volumetric method, using a Micromeritics Gemini VII 2390t. Samples were prepared by gentle manual crushing of the supplied core sample, with minimal use of energy. The crushed material was manually sieved, the measurements were performed on the 63–400 μm size fraction.
About 1 g of crushed sample material was outgassed in a Micromeritics VacPrep 061 for 12 h at room temperature and then heated to 130 °C, under vacuum, for at least 12 h. Adsorption was measured at 42 relative pressure steps between 0.01 and 0.995, and desorption at 29 relative pressure points between 0.995 and 0.1. The nitrogen saturation pressure (P0) was determined separately for each relative pressure point. Sorbate–sorbent equilibrium was assumed when the pressure change over a 10-s interval was <0.01% of the average pressure during the latter interval. The multipoint Brunauer–Emmett–Teller theory (BET) method was applied to quantify the surface area of the analysed sample. A cross-sectional area of the nitrogen molecule of 0.162 nm2 was used (ISO 9277:2010). Total pore volume was determined by means of the Gurvich rule at an interpolated relative pressure of 0.995, assuming the density of adsorbed N2 equals that of liquid N2 at the boiling point (28.8 mol l−1). Pore volume and area distribution were calculated by means of the Barrett–Joyner–Halenda method in accordance with the DIN 66,134 norm. The Harkins–Jura equations with Faas correction were used for calculation of the statistical thickness curves. The reported Barrett–Joyner–Halenda data are calculated from the adsorption branch of the isotherms, assuming half of the pores are open at both ends. Although desorption isotherms are generally advised for pore size distribution (PSD) calculations, these do not give useful data for shales and other geological materials because of the very strong overprint by the tensile strength effect of N2 at ∼40 Å. Repeated measurements on standard materials demonstrated that the accuracy and precision of the methods described above is better than 2% (2σ).
Small angle neutron scattering
Sample porosity and specific surface area was analysed using SANS and VSANS techniques (Fig. 3, Supplementary Figs 4 and 6, and Supplementary Table 3). Experiments were carried out using the instrument KWS-1 (SANS) and KWS-3 (VSANS) operated by the Jülich Center for Neutron Science at Heinz-Meier-Leibnitz Zentrum in Garching, Germany. Carmel caprock samples were cut parallel to bedding, fixed on quartz glass and polished to a thickness of 200 μm for measurements. Samples were dried at room temperature and measurements performed under ambient pressure and temperature conditions. The target area on the sample was defined by a cadmium mask with an 8 mm diameter window.
For (V)SANS measurements, a collimated neutron beam is elastically scattered by the sample48,49. Position-sensitive detectors measure the scattering intensity I(Q) as a function of the scattering angle, which is defined as the angular deviation from the incident beam. The momentum transfer Q (nm−1) is related to the scattering angle θ by Q=(4π/λ)sin(θ/2), where λ is the wavelength of the neutrons. Thus, the size range of features accessible with neutron scattering depends on the neutron wavelength λ and the range in the scattering angle θ. SANS data at KWS-1 were collected at wavelengths of λ=0.69 nm with a wavelength distribution of the velocity selector Δλ/λ=0.10 (full width at half-maximum). Measurements were performed at sample-to-detector distances of 19.7, 7.7 and 1.7 m, covering a wide Q-range of 0.02–2.6 nm−1. The detector was a 6Li glass scintillation detector with an active area of 60 × 60 cm2. VSANS data at KWS-3 were collected at λ=1.28 nm, Δλ/λ=0.2 and a sample-to-detector distance of 9.5 m, covering a Q-range from 0.024 to 0.0016, nm−1. As for KWS-1, a 6Li scintillation detector was used but with a detector diameter of 9 cm. Hence, pore radii for the combined SANS and VSANS measurements range between 1 nm and 1.5 μm (r≈2.5/Q). Instrument data analysis and background subtraction was carried out using the QtiKWS software provided by the Jülich Center for Neutron Science http://iffwww.iff.kfa-juelich.de/pipich/dokuwiki/doku.php/qtikws. During background subtraction, the lower pore sizes were cut off at 12 Å, to remove artefacts arising from Bragg scattering from ordered stacking of clay minerals. For the combined SANS and VSANS measurements, this results in scattering intensity I(Q) (nm−1) versus the momentum transfer, Q (nm−1) relationships on nine samples (Supplementary Fig. 4).
The integral of the scattered intensity in reciprocal space in a two-phase system is the Porod invariant Qinv from which the porosity ϕ is obtained directly48,50:

We assumed that the scattering intensity of pore features is directly proportional to the scattering contrast between matrix and pore48:

Here,  and
and  are the coherent scattering length densities (SLDs) for neutrons for the two phases, shale matrix and air (pore), respectively. The terms P(Q) and S(Q) denote the form and structure factors, for which analytical expressions exist for different geometries of scatterers, including mass and surface fractals48. The SLD Δp* of each mineral was calculated as:
are the coherent scattering length densities (SLDs) for neutrons for the two phases, shale matrix and air (pore), respectively. The terms P(Q) and S(Q) denote the form and structure factors, for which analytical expressions exist for different geometries of scatterers, including mass and surface fractals48. The SLD Δp* of each mineral was calculated as:

where bi and Mi are scattering length and atomic mass of the ith element in the mineral, di is the mass density of the ith mineral and NA is the Avogadro number. The terms ϕ and Vp are the volume fraction of the dispersed phase and the volume per scatterer, respectively. Scattering length densities were calculated using the U.S. National Institute of Science and technology (NSIT) SLD calculator (http://www.ncnr.nist.gov/resources/activation/). As the scattering contrast between the shale matrix and the pores is large, all scattering is attributed to nano-pore features. SLD values for the shale matrix studied range between 3.2 and 3.4 × 10−14 m−2; for air, it can be considered to be zero.
The specific surface area of surface fractals scales with the length scale r as48,51:

where ρ is mass density, Ds is the surface fractal dimension and

Experimentally determined I(Q) curves were modelled, after background subtraction, using the polydisperse hard sphere model implemented in the software code PRINSAS51. Porosity, pore volume and specific surface area values obtained from this analysis are summarized in Supplementary Table 2; intensity, I(Q) and pore frequency distribution f(r) plots for all nine samples analysed are shown in Supplementary Fig. 4. Effective diffusion values De (m2 s−1) were calculated from the fractal dimensions derived from the (V)SANS data (Fig. 3c). Typically, De is related to the diffusion coefficient in water, Dw and the diffusion accessible porosity, ϕ, by

where τ is the tortuosity. Using fractal dimensions derived from (V)SANS measurements; however, the effective diffusion coefficient is related to the diffusion accessible porosity by an analogue empirical power law formulation of the form:

where m is an empirical exponent. In natural porous media the power law form (equation 13) is indicative of the fractal geometry of the pore–solid interface. These fractal dimensions of the pore surface and pore volume can be quantified from (V)SANS analysis. In such a sinuous capillary bundle model, the sinuous nature of the bundle reflects the roughness of the pore–solid interface, with fractal properties within some scale limits. The power law form (equation (13)) can thus be related to the porosity of a volume element of size l2, between the lower and upper limits of the fractal region, l1 and l2, and to the pore volume fractal Dv, as

where, for embedded dimensions of three52, 2≤Dv≤3. The tortuosity(Fig. 3c) of the fractal bundle in a volume element is related to the fractal dimensions of the pore–solid surface, Ds, and pore volume, Dv, as

Substituting equation (15) into equation (12) gives

where the fractal dimensions of the pore surface and pore volume can be quantified from (V)SANS analysis as the slope of Q versus I(Q) and r versus f(r), respectively, in the Q-range 10−4 Å−1≤Q≤10−2 Å−1.
Hydraulic conductivity measurements
A section of core from a red siltstone unit of the lower Carmel Formation (depth: 180.4–180.7 m) was selected during drilling and preserved under mechanical confinement on-site for later analysis in the laboratory. Intrinsic permeability of subsections of the core interval were measured in a bespoke permeameter designed and built by the British Geological Survey. Each core plug sample was carefully manufactured on a machine lathe to minimize damage and desaturation, and to produce samples of known dimension. Samples were then placed inside a single closure pressure vessel and subject to in situ stress and porewater pressure conditions, to hydrate the sample before testing. Permeability was measured by the application of a fixed pressure gradient across each core, while simultaneously measuring flux in and out of the sample. Volumetric flow rates into and out of the core were controlled or monitored using a pair of ISCO-260, Series D, syringe pumps operated from a single digital control unit. The position of each pump piston is determined by an optically encoded disc graduated in segments equivalent to a change in volume of 16.6 nl. Movement of the pump piston is controlled by a micro-processor that continuously monitors and adjusts the rate of rotation of the encoded disc using a DC motor connected to the piston assembly via a geared worm drive. This allows each pump to operate in either constant pressure or constant flow modes. A programme written in LabVIEW elicits data from the pump at pre-set time intervals. Testing was performed in an air-conditioned laboratory at a nominal temperature of 20 °C.
Darcy’s law gives the following relationship for the conductivity, K,

where Q is the steady-state flow (m3 s−1), pw is the density of water (kg m−3), g is the acceleration due to gravity (m s−2), As is the cross-sectional area of the test sample normal to flow (m2), ΔLs is the sample length (m) and ΔP is the pressure drop along the sample (Pa). The equivalent permeability term (k) is given by

where μw is the viscosity of water (1.002 × 10−3 Pa s). Measurements on the four selected core intervals gave permeabilities between 5 × 10−22 and 1.2 × 10−21 m2 with an average value of 9.1 × 10−22 m2 (1σ=2.3 × 10−22 m2).
Reaction rates for dolomite and haematite
Dolomite dissolution rates are given by Pokrovsky et al.53 who modelled experimental determinations of dolomite dissolution rates by various pH-dependent surface processes. At the intermediate pH conditions and CO2 partial pressures in the cap rock, the predicted reaction rates are between 5 × 10−7 and 10−5 mol m−2 s−1. dos Santos Afonso and Stumm41 measured haematite dissolution rates as a function of pH and H2S concentrations. For the pH and estimated partial pressures of H2S in the caprock, the predicted dissolution rates lie between 10−10 and 10−8 mol m−2 s−1.
Reactive transport modelling with analytical solution
Advective flow rates, (ω0ϕ) where ω0 is fluid velocity and ϕ porosity, through the caprock are estimated to be <6 × 10−12 m s−1 given permeabilities of ∼10−21 m2 and a piezometric pressure gradient of ∼104 to 4 × 106 Pa m−1 taking the hydraulic head in the Navajo54 either across the whole Carmel Formation or the 16 cm basal seal. With effective diffusivities (De) of components in the fluid phase of ∼10−11 to 10−12 m2, the Péclet number (ω0ϕh/De) for advective–diffusive transport of a compatible component would be in the range 10−7 to 10−2, values that imply advective transport is negligible consistent with the analysis of the caprock transport. We therefore model reactive transport in the caprock driven only by diffusion.
The equation describing one-dimensional diffusive transport with mineral reaction of solute concentration C (mol m−3) with respect to distance x (m), time t (s), effective diffusivity D (m2 s−1), porosity ϕ, tortuosity, τ2, mineral reaction rate kf (m s−1) and surface area α (m2 m−3) can be written as39

where (Ceq−C) describes a linear dependence of the reaction rate to the difference between the solute component concentration, C (mol m−3) and its concentration at equilibrium, Ceq, with the reacting mineral. The mineral molar concentration in the rock, ϕs (mol m−3), then varies according to

Making the transformation to dimensionless variable by

where l (m) is a transport distance taken as the displacement of the reaction front, De is the effective diffusion coefficient ϕD/τ2 and C0 is solute concentration in the input fluid. Substituting equation (21) into equations (19) and (20) gives


dependent on the dimensionless constant, the Damköhler number ND, defined by

For reaction rates of dolomite (kR) between 10−6 and 10−8 mol m−2 s−1 (note kf=kRVS where VS is the molar volume of dolomite) and diffusion coefficients in the range 1 × 10−11 to 5 × 10−12 m2 s−1, Damköhler numbers are in the range 5 × 107 to 9 × 109 and fluids will be effectively in local equilibrium with minerals. For haematite with reaction rates in the range 10−8 to 10−12 mol m−2 s−1, Damköhler numbers are in the range 2 × 103 to 3 × 107 and haematite will be close to equilibrium wherever it is in contact with CO2 transported by diffusion.
On initiation of diffusion, dissolution of the reactive mineral takes place at a rate, which decreases away from the inlet such that the mineral is exhausted after time τ0 (s) given by

or in dimensionless time,

At times greater than τ0, the reactive mineral is exhausted over distances x≤l. Where concentrations in the fluid are small compared with those in the solid and porosities are small, the approximate quasi-stationary state solutions to equations (19) and (20) are valid39. Solutions for fluid compositions and solid mineral modes, assuming mineral surface area remains constant, following ref. 39, in dimensionless coordinates for τ0>0, are (note l′=1)


where ΔC0=Ceq−C0. ΔC0 for Fe2O3 in reaction (1), between the inlet solution and a solution at equilibrium with haematite, has been calculated using PHREEQC42 as 2.95 mol m−3 for an inlet solution with the average composition of the fluids sampled downhole in the Navajo Sandstone, with a range from 1.9 to 3.95 mol m−3 reflecting the range in pH of 5.3–5.1 of the downhole fluids23. It is noteworthy that the Damköhler number, ND=(ql)2, with q (m−1) defined by Lichtner39 as the exponential constant giving the length scale over which fluid returns to equilibrium with the initial mineralogy. The time for the reaction front to migrate to distance, l, (l′=1) is given by solution of

or in terms of dimensional constants

Multicomponent reactive transport modelling
PHREEQC modelling was conducted using the llnl.dat thermodynamic data base thermo.com.V8.R6.230 (ref. 42). A 15-cm-long one-dimensional reactive–diffusive model comprising 30 cells of 5 mm length was constructed. The initial mineralogy (mol l−1) was calculated from quantitative mineralogy determined by XRD, using pore volumes measured from SANS of the unaltered portion of the caprock. The invading pore fluid chemistry was based on analyses of the reservoir fluids (Supplementary Table 4) and the initial caprock pore fluid chemistry was taken to be a fluid in equilibrium with the caprock mineralogy, with pCO2, pO2 and salinity estimates for typical Jurassic marine shales. The initial redox state of the invading fluid was defined using the SO4 2−/H2S redox couple. Models were run assuming local fluid–mineral equilibrium. A constant De value of 5 × 10−12 m2 s−1 was used for all aqueous species. The model timescale was 125,000 years with a time step of 7 days. The thermodynamic database was supplemented with data for Fe-dolomite (CaMg0.9Fe0.1(CO3)2) calculated using ideal mixing laws and the thermodynamic data for ankerite taken from ToughReact TherAkin8.dat.
A second model was constructed comprising two 25,000 year pulses of CO2-charged brine injection separated by a 75,000 year period where a hypothetical CO2-poor brine was diffused into the model cells (Fig. 4b). The durations of each pulse were chosen to mimic the timescale of periodic degassing of CO2 previously document for the local fault systems26.
Data availability
The authors declare that the data supporting the findings of this study are available within the article and its Supplementary Information files.
Additional information
How to cite this article: Kampman, N. et al. Observational evidence confirms modelling of the long-term integrity of CO2-reservoir caprocks. Nat. Commun. 7:12268 doi: 10.1038/ncomms12268 (2016).
References
Metz, B., Davidson, O., de Coninck, H. C., Loos, M. & Meyer, L. A. IPCC Special Report on Carbon Dioxide Capture and Storage. Prepared by working Group III of the Intergovernmental Panel on Climate Change 442(Cambridge Univ. Press (2005).
Benson, S. M. & Cole, D. R. CO2 sequestration in deep sedimentary formations. Elements 4, 325–331 (2008).
Bickle, M. J. Geological carbon storage. Nat. Geosci. 2, 815–818 (2009).
Busch, A. & Amann-Hildenbrand, A. Predicting capillarity of mudrocks. Marine Petrol. Geol. 45, 208–223 (2013).
Gaus, I., Azaroual, M. & Czernichowski-Lauriol, I. Reactive transport modelling of the impact of CO2 injection on the clayey cap rock at Sleipner (North Sea). Chem. Geol. 217, 319–337 (2005).
Johnson, J. W., Nitao, J. J. & Morris, J. P. Reactive transport modeling of cap-rock integrity during natural and engineered CO2 storage. Carbon Dioxide Capture for Storage in Deep Geologic Formations 2, 787 (2004).
Liu, F. et al. CO2–brine–caprock interaction: reactivity experiments on Eau Claire shale and a review of relevant literature. Int. J. Greenhouse Gas Control 7, 153–167 (2012).
Rutqvist, J. The geomechanics of CO2 storage in deep sedimentary formations. Geotech. Geol. Eng. 30, 525–551 (2012).
Gherardi, F., Xu, T. & Pruess, K. Numerical modeling of self-limiting and self-enhancing caprock alteration induced by CO2 storage in a depleted gas reservoir. Chem. Geol. 244, 103–129 (2007).
Knauss, K. G., Johnson, J. W. & Steefel, C. I. Evaluation of the impact of CO2, co-contaminant gas, aqueous fluid and reservoir rock interactions on the geologic sequestration of CO2 . Chem. Geol. 217, 339–350 (2005).
Bildstein, O. et al. Integrative modeling of caprock integrity in the context of CO2 storage: evolution of transport and geochemical properties and impact on performance and safety assessment. Oil Gas Sci. Techn. 65, 485–502 (2010).
Balashov, V., Guthrie, G., Lopano, C. L., Hakala, J. A. & Brantley, S. L. Reaction and diffusion at the reservoir/shale interface during CO2 storage: impact of geochemical kinetics. Appl. Geochem. 61, 119–131 (2015).
Tambach, T. J., Koenen, M., Wasch, L. J. & van Bergen, F. Geochemical evaluation of CO 2 injection and containment in a depleted gas field. Int. J. Greenhouse Gas Control 32, 61–80 (2015).
Armitage, P., Faulkner, D. & Worden, R. Caprock corrosion. Nat. Geosci. 6, 79–80 (2013).
Tarkowski, R., Wdowin, M. & Manecki, M. Petrophysical examination of CO2-brine-rock interactions—results of the first stage of long-term experiments in the potential Zaosie Anticline reservoir (central Poland) for CO2 storage. Environ. Monitor. Assess. 187, 1–10 (2015).
Amann-Hildenbrand, A., Bertier, P., Busch, A. & Krooss, B. M. Experimental investigation of the sealing capacity of generic clay-rich caprocks. Int. J. Greenhouse Gas Control 19, 620–641 (2013).
Bolourinejad, P. & Herber, R. Experimental investigation of porosity and permeability variations in reservoirs and caprock following co-injection of sulfur dioxide and hydrogen sulfide with carbon dioxide. J. Petrol. Sci. Eng. 129, 137–144 (2015).
Busch, A. et al. Carbon dioxide storage potential of shales. Int. J. Greenhouse Gas Control 2, 297–308 (2008).
White, A. & Brantley, S. The effect of time on the weathering of silicate minerals: why do weathering rates differ in the laboratory and field? Chem. Geol. 202, 479–506 (2003).
Steefel, C. I. & Maher, K. Fluid-rock interaction: a reactive transport approach. Revi. Mineral. Geochem. 70, 485–532 (2009).
Palandri, J. L. & Kharaka, Y. K. Ferric iron-bearing sediments as a mineral trap for CO2 sequestration: iron reduction using sulfur-bearing waste gas. Chem. Geol. 217, 351–364 (2005).
Kampman, N. et al. Scientific drilling and downhole fluid sampling of a natural CO2 reservoir, Green River, Utah. Sci. Drill. 16, 33–43 (2013).
Kampman, N. et al. Drilling and sampling a natural CO2 reservoir: implications for fluid flow and CO2-fluid–rock reactions during CO2 migration through the overburden. Chem. Geol. 369, 51–82 (2014).
Heath, J. E., Lachmar, T. E., Evans, J. P., Kolesar, P. T. & Williams, A. P. in Geophysical Monograph Series 183, eds McPherson B. J., Sundquist E. T. Ch. 10 147–158American Geophysical Union (2009).
Burnside, N. M., Shipton, Z. K., Dockrill, B. & Ellam, R. M. Man-made versus natural CO2 leakage: a 400 k.y. history of an analogue for engineered geological storage of CO2 . Geology 41, 471–474 (2013).
Kampman, N. et al. Pulses of carbon dioxide emissions from intracrustal faults following climatic warming. Nat. Geosci. 5, 352–358 (2012).
Blakey, R. C., Havholm, K. G. & Jones, L. S. Stratigraphic analysis of eolian interactions with marine and fluvial deposits, Middle Jurassic Page Sandstone and Carmel Formation, Colorado Plateau, USA. J. Sediment. Res. 66, 324–342 (1996).
Armitage, P. et al. Mercia Mudstone Formation caprock to carbon capture and storage sites: petrology and petrophysical characteristics. J. Geol. Soc. Lond. 170, 119–132 (2013).
Goethel, M. Schlussfolgerungen ueber Untersuchungen zum Rhaet/Lias in der Vetschauer Keupermulde (Lausitzer Triasscholle). Brandenburgische Geowiss Beitr 6, 65–77 (1999).
Kampman, N., Bickle, M. J., Wigley, M. & Dubacq, B. Fluid flow and CO2–fluid–mineral interactions during CO2-storage in sedimentary basins. Chem. Geol. 369, 22–50 (2014).
Wigley, M., Kampman, N., Dubacq, B. & Bickle, M. Fluid-mineral reactions and trace metal mobilisation in an exhumed natural CO2 reservoir, Green River, Utah. Geology 40, 555–558 (2012).
Wigley, M., Dubacq, B., Kampman, N. & Bickle, M. Controls of sluggish, CO2-promoted, hematite and K-feldspar dissolution kinetics in sandstones. Earth Planet. Sci. Lett. 362, 76–87 (2013).
Tamimi, A., Rinker, E. B. & Sandall, O. C. Diffusion coefficients of hydrogen sulfide, carbon dioxide, and nitrous oxide in water over the temperature range 293–368 K. J. Chem. Eng. Data 39, 330–332 (1994).
Clarkson, C. R. et al. Pore structure characterization of North American shale gas reservoirs using USANS/SANS, gas adsorption, and mercury intrusion. Fuel Process. Technol. 103, 606–616 (2013).
Bertier, P. et al. in The Clay Minerals Society Workshop Lectures Series 21, Ch. 12 eds Schäfer T., Dohrmann R., Greenwell H. C. 151–161Clay Minerals Society (2016).
Amann-Hildenbrand, A., Bertier, P., Busch, A. & Krooss, B. M. Experimental investigation of the sealing capacity of generic clay-rich caprocks. Int. J. Greenhouse Gas Control 19, 620–641 (2013).
Berne, P., Bachaud, P. & Fleury, M. Diffusion properties of carbonated caprocks from the Paris Basin. Oil Gas Sci. Technol. 65, 473–484 (2010).
Wollenweber, J. et al. Caprock and overburden processes in geological CO2 storage: an experimental study on sealing efficiency and mineral alterations. Energy Proc. 1, 3469–3476 (2009).
Lichtner, P. C. The quasi-stationary state approximation to coupled mass transport and fluid rock interaction in a porous medium. Geochim. Cosmochim. Acta 52, 143–165 (1988).
Baker, J. & Spiegelman, M. Modelling an infitration-driven geochemical front. Earth Planet. Sci. Lett. 136, 87–96 (1995).
dos Santos Afonso, M. & Stumm, W. Reductive dissolution of iron (III) (hydr) oxides by hydrogen sulfide. Langmuir 8, 1671–1675 (1992).
Parkhurst, D. L. & Appelo, C. A. J. in U.S. Geological Survey Techniques and Methods Ch. A43, Book Vol 6, http://pubs.usgs.gov/tm/06/a43/497(USGS (2013).
Turrero, M. J. et al. Pore water chemistry of a Paleogene continental mudrock in Spain and a Jurassic marine mudrock in Switzerland: Sampling methods and geochemical interpretation. J. Iberian Geol. 32, 233–258 (2006).
Shipton, Z. K., Evans, J. P., Robeson, K. R., Forster, C. B. & Snelgrove, S. Structural heterogeneity and permeability in faulted eolian sandstone: Implications for subsurface modeling of faults. AAPG Bull. 86, 863–883 (2002).
Gasparik, M. et al. Geological controls on the methane storage capacity in organic-rich shales. Int. J. Coal Geol. 123, 34–51 (2014).
Ufer, K. et al. Quantitative phase analysis of bentonites by the rietveld method. Clays Clay Minerals 56, 272–282 (2008).
Bickle, M. J., Tipper, E. D., Galy, A., Chapman, H. J. & Harris, N. W. B. On discrimination between carbonate and silicate inputs to Himalayan rivers. Am. J. Sci. 315, 120–166 (2015).
Radlinski, A. P. Small-angle neutron scattering and the microstructure of rocks. Rev. Mineral. Geochem. 63, 363–397 (2006).
Guinier, A. & Fournet, G. Small-Angle Scattering of X-rays John Wiley and Sons (1955).
Porod, G. in Small-Angle X-ray Scattering eds Glatter O., Kratky O. 17–51Academic Press (1982).
Hinde, A. PRINSAS- a Windows-based computer program for the processing and interpretation of small-angle scattering data tailored to the analysis of sedimentary rocks. J. Appl. Crystallogr. 37, 1020–1024 (2004).
Liu, J.-g., Wang, H.-t. & Nie, Y.-f. Fractal model for predicting effective diffusion coefficient of solute in porous media. Adv. Water Sci. 15, 458–462 (2004).
Pokrovsky, O. S., Golubev, S. V., Schott, J. & Castillo, A. Calcite, dolomite and magnesite dissolution kinetics in aqueous solutions at acid to circumneutral pH, 25 to 150 °C and 1 to 55 atm pCO2: New constraints on CO2 sequestration in sedimentary basins. Chem. Geol. 265, 20–32 (2009).
Hood, J. W. & Patterson, D. J. Bedrock aquifers in the northern San Rafael Swell area, Utah, with special emphasis on the Navajo Sandstone. State of Utah Department of Natural Resources. Technical Publication, 78, 1–128 (1984).
Acknowledgements
We thank DOSECC for carrying out the drilling, Morgan Schaller for coordinating activities on the drill site, the core logging team from Utah State University and staff at the Godwin Laboratory, Cambridge for O- and C-isotopic analyses. Funding was provided by NERC to the CRIUS consortium (NE/F004699/1), Shell Global Solutions, for GR as part of the Center for Nanoscale Controls on Geologic CO2 (NCGC), an Energy Frontier Research Center funded by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences (BES), under Award # DE-AC02-05CH11231, and DECC, which provided a CCS Innovation grant for completion of this work. Data from the British Geological Survey is published with the permission of the Executive Director, British Geological Survey (NERC).
Author information
Authors and Affiliations
Contributions
M.J.B., N.K. and A.B. conceived the project, which was based on extensive previous work at Green River by N.K. and M.J.B. and co-workers. P.B. performed the XRD analyses. H.J.C. performed the Sr-isotope analyses. J.F.H. performed the permeability measurements and P.B. performed the N2-BET measurements. N.K. performed the scanning electron microscopy and EMPA analyses. A.B., N.K., P.B., V.P., Z.D. and G.R. carried out the SANS and VSANS measurements. J.E. and N.K. coordinated the drilling. N.K., J.S. and M.J.B. were responsible for the modelling. N.K., M.J.B. and A.B. wrote the paper with contributions by all the authors.
Corresponding author
Ethics declarations
Competing interests
N.K., A.B. and J.S. are employed by Shell Global Solutions International. All other authors delare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-6, Supplementary Tables 1-4 and Supplementary References (PDF 1403 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Kampman, N., Busch, A., Bertier, P. et al. Observational evidence confirms modelling of the long-term integrity of CO2-reservoir caprocks. Nat Commun 7, 12268 (2016). https://doi.org/10.1038/ncomms12268
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms12268
This article is cited by
-
In-situ experiment reveals CO2 enriched fluid migration in faulted caprock
Scientific Reports (2023)
-
Chemo-mechanical Alteration of Silicate-Rich Shale Rock after Exposure to CO2-Rich Brine at High Temperature and Pressure
Rock Mechanics and Rock Engineering (2023)
-
Mineral reaction kinetics constrain the length scale of rock matrix diffusion
Scientific Reports (2020)
-
Pore-scale characteristics of multiphase flow in heterogeneous porous media using the lattice Boltzmann method
Scientific Reports (2019)
-
New insights on the complex dynamics of two-phase flow in porous media under intermediate-wet conditions
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.