Abstract
Reliable quantum information processing in the face of errors is a major fundamental and technological challenge. Quantum error correction protects quantum states by encoding a logical quantum bit (qubit) in multiple physical qubits. To be compatible with universal fault-tolerant computations, it is essential that states remain encoded at all times and that errors are actively corrected. Here we demonstrate such active error correction on a continuously protected logical qubit using a diamond quantum processor. We encode the logical qubit in three long-lived nuclear spins, repeatedly detect phase errors by non-destructive measurements, and apply corrections by real-time feedback. The actively error-corrected qubit is robust against errors and encoded quantum superposition states are preserved beyond the natural dephasing time of the best physical qubit in the encoding. These results establish a powerful platform to investigate error correction under different types of noise and mark an important step towards fault-tolerant quantum information processing.
Similar content being viewed by others
Introduction
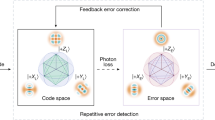
Large-scale quantum information processing requires the correction of errors during computations. In quantum error correction, a logical quantum bit (qubit) is encoded in a subspace of multiple physical qubits so that errors can be actively corrected without affecting the encoded information. A promising way to correct errors in encoded quantum states is to perform feedback based on multi-qubit measurements known as stabilizer measurements1,2,3 (see Fig. 1a for details). These measurements are performed non-destructively using extra qubits (ancillas) and are frequently repeated to detect errors before they accumulate. The measurement outcomes are then processed in classical logic that identifies the error syndrome, and, in order to enable universal computations1, active feedback is applied to the encoded system to correct errors where needed. The key experimental challenge is to perform such complete error-correction cycles including non-destructive stabilizer measurements and real-time feedback well within the coherence time.
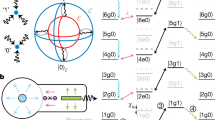
(a) A quantum state is encoded in a logical qubit consisting of three physical qubits. Errors inevitably occur, for example, during computations. An ancilla is used to repeatedly perform measurements that detect errors. Errors are corrected through classical logic and feedback, while the quantum state remains coherent and encoded. (b) Device: chemical-vapour-deposition-grown single-crystal diamond with a solid-immersion lens37 and on-chip lines for microwave control. Scale bar, 5 μm. Ancilla: the optically addressable electronic spin of a nitrogen vacancy (NV) centre. Qubits: three 13C nuclear spins that are controlled and measured through the hyperfine coupling to the ancilla (Methods). (c) Free induction decay (Ramsey) experiments. Gaussian fits yield dephasing times  =12.0(9), 9.1(6) and 18.2(9) ms for qubits 1, 2 and 3, respectively. (d) Deterministic entanglement of two qubits by XX stabilizer measurement and feedback. The ±x gates are π/2 rotations around x with the sign controlled by the ancilla state. The final X operations reset the ancilla and account for an additional X flip for the +1 outcome (Methods). (e) State tomography of the generated entangled state for qubits 2 and 3. The fidelity with the ideal state is F=0.824(7) (see Supplementary Fig. 6 for other qubit combinations and post-selected results). All error bars are one statistical s.d.
=12.0(9), 9.1(6) and 18.2(9) ms for qubits 1, 2 and 3, respectively. (d) Deterministic entanglement of two qubits by XX stabilizer measurement and feedback. The ±x gates are π/2 rotations around x with the sign controlled by the ancilla state. The final X operations reset the ancilla and account for an additional X flip for the +1 outcome (Methods). (e) State tomography of the generated entangled state for qubits 2 and 3. The fidelity with the ideal state is F=0.824(7) (see Supplementary Fig. 6 for other qubit combinations and post-selected results). All error bars are one statistical s.d.
Quantum-error-correction protocols have been explored across a range of platforms4,5,6,7,8,9,10,11,12,13,14. Pioneering experiments bypassed stabilizer measurements by reversing the encoding to correct errors, thus leaving the quantum state unprotected5,6,7,8,9,10,11. Recent breakthroughs have enabled the use of stabilizer measurements to passively track errors in quantum states and retrieve stored information afterwards through post processing12,13,14,15.
Here we realize complete rounds of active quantum error correction on a continuously encoded logical qubit by exploiting newly developed stabilizer measurements based on an electron spin ancilla with high-fidelity non-demolition readout, by encoding in long-lived nuclear spins, and by applying real-time correction of errors through fast classical logic. We show that the actively error-corrected logical qubit is robust against errors and that multiple rounds of error correction prevent errors from accumulating. Finally, by correcting time-correlated phase errors naturally induced by the environment, we demonstrate that encoded quantum superposition states are preserved beyond the dephasing time of the best physical qubit used in the encoding.
Results
Error correction code
The three-qubit code considered here corrects a single phase error on any one of the physical qubits. To protect against such errors, we encode the logical qubit in states for which all physical qubits have the same phase:  with
with 
 and
and  . Errors (Z operations) are detected by measuring the two stabilizer generators X1X2I3 and I1X2X3 via an ancilla. These measurements, respectively, compare the phases of qubits 1 and 2 and qubits 2 and 3. For an uncorrupted state, both measurements yield outcome +1 (same phase, no error), but for a phase error on just one of the qubits, the two measurements give a unique syndrome of −1 outcomes that identifies the error. For example, an error on the first qubit results in outcome −1 for the first stabilizer measurement and outcome +1 for the second. The logical qubit operators are XL=X1I2I3, YL=Y1Z2Z3 and ZL=Z1Z2Z3 (or their permutations).
. Errors (Z operations) are detected by measuring the two stabilizer generators X1X2I3 and I1X2X3 via an ancilla. These measurements, respectively, compare the phases of qubits 1 and 2 and qubits 2 and 3. For an uncorrupted state, both measurements yield outcome +1 (same phase, no error), but for a phase error on just one of the qubits, the two measurements give a unique syndrome of −1 outcomes that identifies the error. For example, an error on the first qubit results in outcome −1 for the first stabilizer measurement and outcome +1 for the second. The logical qubit operators are XL=X1I2I3, YL=Y1Z2Z3 and ZL=Z1Z2Z3 (or their permutations).
Stabilizer measurements and real-time feedback
Our qubits are three 13C nuclear spins (I=1/2, 1.1% abundance) surrounding a single nitrogen-vacancy (NV) centre in diamond, whose electronic spin we use as ancilla (S=1;  and
and  ; Fig. 1b). At 4 K, the ancilla combines fast control16, optical single-shot readout17 and long coherence times18 (>25 ms, Methods). We use relatively remote nuclear qubits (coupling to the ancilla 20–50 kHz) that are robust against optical excitation of the ancilla and design decoherence-protected gates to control them9,19 (Methods). All three qubits show long dephasing times
; Fig. 1b). At 4 K, the ancilla combines fast control16, optical single-shot readout17 and long coherence times18 (>25 ms, Methods). We use relatively remote nuclear qubits (coupling to the ancilla 20–50 kHz) that are robust against optical excitation of the ancilla and design decoherence-protected gates to control them9,19 (Methods). All three qubits show long dephasing times  with the dominant natural errors being phase errors (Fig. 1c).
with the dominant natural errors being phase errors (Fig. 1c).
The key challenge for implementing stabilizer measurements in this system is that the ancilla–qubit interaction is always present: imperfect knowledge of the ancilla state during or after readout dephases the qubits20,21,22. To minimize this dephasing, we implement quantum non-demolition measurements of the ancilla by resonant optical excitation of  and by stopping the excitation within 2 μs upon photon detection (outcome
and by stopping the excitation within 2 μs upon photon detection (outcome  ) to minimize uncontrolled spin flips in the optically excited state23 (Methods). The resulting readout fidelities are F0=0.890(4) for
) to minimize uncontrolled spin flips in the optically excited state23 (Methods). The resulting readout fidelities are F0=0.890(4) for  and F1=0.988(2) for
and F1=0.988(2) for  (average: F=0.939(2)). Crucially, the post-measurement fidelity after correctly assigning
(average: F=0.939(2)). Crucially, the post-measurement fidelity after correctly assigning  is 0.992, demonstrating the desired non-demolition character.
is 0.992, demonstrating the desired non-demolition character.
To benchmark the stabilizer measurements and real-time feedback, we deterministically entangle two qubits by projecting into a Bell state, that is, a simultaneous eigenstate of XX and ZZ21,24,25. First, the qubits are initialized in  , an eigenstate of ZZ, with fidelity 0.910(6). Then, a XX stabilizer measurement projects the qubits onto one of two Bell states (Fig. 1d). We interpret the −1 outcome as an error in the desired state and correct it through feedback before performing two-qubit tomography. The deterministically generated entangled state, with fidelity F=0.824(7) (Fig. 1e), demonstrates the non-destructive nature of the measurement; coherence within the subspaces is maintained throughout the measurement and feedback cycle. The complete cycle can be repeated up to six times within the shortest qubit
, an eigenstate of ZZ, with fidelity 0.910(6). Then, a XX stabilizer measurement projects the qubits onto one of two Bell states (Fig. 1d). We interpret the −1 outcome as an error in the desired state and correct it through feedback before performing two-qubit tomography. The deterministically generated entangled state, with fidelity F=0.824(7) (Fig. 1e), demonstrates the non-destructive nature of the measurement; coherence within the subspaces is maintained throughout the measurement and feedback cycle. The complete cycle can be repeated up to six times within the shortest qubit  .
.
Active quantum error correction on a logical qubit
We now turn to quantum error correction by stabilizer measurements. The logical qubit is encoded by mapping an arbitrary state  prepared on the ancilla to the three-qubit state
prepared on the ancilla to the three-qubit state  (Fig. 2a). We characterize the encoding by preparing six basis states
(Fig. 2a). We characterize the encoding by preparing six basis states  ,
,  ,
,  and
and  and performing three-qubit state tomography. The fidelities with the ideal states confirm successful encoding and genuine three-qubit entanglement (Fig. 2b).
and performing three-qubit state tomography. The fidelities with the ideal states confirm successful encoding and genuine three-qubit entanglement (Fig. 2b).
(a) Encoding an arbitrary quantum state  prepared on the ancilla into
prepared on the ancilla into  . Successful encoding is heralded by outcome
. Successful encoding is heralded by outcome  . (b) Characterization of the logical states
. (b) Characterization of the logical states  ,
,  and
and  . Only the logical qubit operators and stabilizers are shown (see Supplementary Fig. 7 for complete tomography of all 6 logical basis states). The fidelities with the ideal three-qubit states are F=0.810(5), 0.759(5)and 0.739(5), respectively, demonstrating three-qubit entanglement10. The logical state fidelities are
. Only the logical qubit operators and stabilizers are shown (see Supplementary Fig. 7 for complete tomography of all 6 logical basis states). The fidelities with the ideal three-qubit states are F=0.810(5), 0.759(5)and 0.739(5), respectively, demonstrating three-qubit entanglement10. The logical state fidelities are  ,
,  and
and  . Ideally, all the encoded states are +1 eigenstates of the stabilizers X1X2I3 and I1X2X3. The fidelity to this code space,
. Ideally, all the encoded states are +1 eigenstates of the stabilizers X1X2I3 and I1X2X3. The fidelity to this code space,  , is 0.839(3) averaged over all states and gives the probability that the starting state is free of detectable errors. All error bars are one statistical s.d.
, is 0.839(3) averaged over all states and gives the probability that the starting state is free of detectable errors. All error bars are one statistical s.d.
We first investigate the recovery of arbitrary logical qubit states from phase errors. To emulate a general process causing dephasing, uncorrelated incoherent errors are applied with variable probability pe to each physical qubit simultaneously (Fig. 3a); for each qubit, the error process is  , with ρ the single-qubit density matrix. By controllably applying such errors, we characterize the effectiveness of the error correction for any process causing uncorrelated errors with equal probability to the qubits. We then measure the stabilizers X1X2I3 and I1X2X3, identify potential errors and correct them through feedback. The probabilities to obtain the four different error syndromes (inset in Fig. 3b) show the expected symmetry around pe=0.5 and match the theoretical prediction based on the errors present in the initial states (Fig. 2b) and the average ancilla readout fidelity.
, with ρ the single-qubit density matrix. By controllably applying such errors, we characterize the effectiveness of the error correction for any process causing uncorrelated errors with equal probability to the qubits. We then measure the stabilizers X1X2I3 and I1X2X3, identify potential errors and correct them through feedback. The probabilities to obtain the four different error syndromes (inset in Fig. 3b) show the expected symmetry around pe=0.5 and match the theoretical prediction based on the errors present in the initial states (Fig. 2b) and the average ancilla readout fidelity.
(a) All qubits are simultaneously subjected to uncorrelated phase errors E with probability pe. Errors are detected by measuring X1X2I3 and I1X2X3 and subsequently corrected by Z operations through feedback. Finally, we measure the process fidelity with the identity. (b) Process fidelities for: an unencoded qubit (averaged over the three qubits), the logical qubit without stabilizer measurements, the error-corrected logical qubit and the logical qubit without feedback (that is, errors are detected but not corrected). We average over the logical qubit permutations, for example, XL=X1I2I3, I1X2I3 and I1I2X3, and the four ways to assign the ancilla states to the error syndromes (see Supplementary Fig. 8 for individual curves). Inset: probabilities for the error syndromes with theoretically predicted curves based on the state tomography in Fig. 2b (Supplementary Note 2). (c) Comparison between the error-corrected logical qubit and the logical qubit with the stabilizer measurements replaced by an equivalent idle time (2.99 ms). Compared with b, the effective readout fidelity is optimized by associating syndrome +1, +1 (no error) to obtaining  for both stabilizer measurements. Curves in b,c are fits described in the Methods. All error bars are one statistical s.d.
for both stabilizer measurements. Curves in b,c are fits described in the Methods. All error bars are one statistical s.d.
The protection of the logical qubit is characterized by the process fidelity with the identity (Fig. 3b; Methods). We quantitatively analyse the results by fitting to  , where FQEC(pe) and Flinear(pe) are the theoretical curves with and without error correction (w=1 indicates ideal robustness against applied single-qubit errors). When no error correction is applied we observe the expected linear dependence on the error probability: w≈0. In contrast, with quantum error correction w is 0.81(3), and a nonlinear curve shape that is characteristic for robustness against single-qubit errors is obtained. This result demonstrates that the entropy associated to the applied errors is successfully removed from the system.
, where FQEC(pe) and Flinear(pe) are the theoretical curves with and without error correction (w=1 indicates ideal robustness against applied single-qubit errors). When no error correction is applied we observe the expected linear dependence on the error probability: w≈0. In contrast, with quantum error correction w is 0.81(3), and a nonlinear curve shape that is characteristic for robustness against single-qubit errors is obtained. This result demonstrates that the entropy associated to the applied errors is successfully removed from the system.
Comparisons to an unencoded qubit and the logical qubit without error correction reveal that adding quantum error correction on top of a computation does not yet provide a net improvement (Fig. 3b), because of additional errors introduced by the initialization, encoding and stabilizer measurements (total of 13 two-qubit gates, 488 ancilla refocusing pulses and 6 ancilla readouts/resets). To isolate the errors due to the stabilizer measurements, we compare the error-corrected logical qubit to the logical qubit left idle. We further optimize the error correction, by assigning the ancilla state with the best readout fidelity ( , F1=0.988(2)) to the most likely error syndrome (+1, +1—no error, inset Fig. 3b), instead of averaging over all assignments as in Fig. 3b. With this improvement, error correction outperforms idling for a range of pe (Fig. 3c); once the logical qubit is encoded, quantum error correction can be beneficial.
, F1=0.988(2)) to the most likely error syndrome (+1, +1—no error, inset Fig. 3b), instead of averaging over all assignments as in Fig. 3b. With this improvement, error correction outperforms idling for a range of pe (Fig. 3c); once the logical qubit is encoded, quantum error correction can be beneficial.
Multiple rounds of active error correction
Because a complete round of error correction (2.99 ms) fits well within the dephasing time of the physical qubits, we can concatenate multiple rounds to improve the coherence of continuously encoded quantum superpositions by preventing the accumulation of errors (Fig. 4a). Three new elements are introduced. First, the total error probability pe is distributed over n rounds, so that the error probability per round is  (Methods). This error model corresponds to errors occurring incoherently, for example with a constant rate in time. Second, to investigate dephasing we focus on the protection of the two states
(Methods). This error model corresponds to errors occurring incoherently, for example with a constant rate in time. Second, to investigate dephasing we focus on the protection of the two states  (that is, a classical bit stored in the phase of a quantum superposition). Third, we exploit the intrinsic robustness of the logical qubit to single Z errors by redefining
(that is, a classical bit stored in the phase of a quantum superposition). Third, we exploit the intrinsic robustness of the logical qubit to single Z errors by redefining  , which is equivalent to performing a round of error correction by majority voting at the end of the experiment13,14.
, which is equivalent to performing a round of error correction by majority voting at the end of the experiment13,14.
(a) Three rounds of error correction on a logical qubit. The first two rounds of quantum error correction use stabilizer measurements and feedback. The final round is implemented by majority voting. (b) Average logical state fidelity for  and
and  as a function of total error probability pe for n=1, 2 and 3 rounds of error correction compared with an unencoded qubit. The errors per round En occur with probability pn. Inset: probabilities that no error is detected (n=3). The similarity of the results for rounds A and B confirms that errors are corrected in between rounds. (c) Correcting natural dephasing. The storage time is defined from the end of the encoding until the start of the final measurements. (d) Dephasing of the logical qubit: without stabilizer measurements, with quantum error correction and without feedback, compared with the best unencoded qubit. The dashed lines indicate the times between which the actively error-corrected logical qubit gives the highest fidelity. The data without feedback (detecting errors without correcting) isolate the suppression of coherently evolving errors by projecting them. For long times, applying error correction lowers the fidelity because the stabilizer measurements extract no useful information about errors, but nevertheless preferentially suppress evolutions that result in phase errors at the end of the sequence (see Supplementary Fig. 10 for a detailed analysis). See Supplementary Fig. 9 for error syndrome probabilities. Solid curves in b,d are fits described in the Methods and Supplementary Notes 1 and 2. Dashed lines are a guide to the eye. All error bars are one statistical s.d.
as a function of total error probability pe for n=1, 2 and 3 rounds of error correction compared with an unencoded qubit. The errors per round En occur with probability pn. Inset: probabilities that no error is detected (n=3). The similarity of the results for rounds A and B confirms that errors are corrected in between rounds. (c) Correcting natural dephasing. The storage time is defined from the end of the encoding until the start of the final measurements. (d) Dephasing of the logical qubit: without stabilizer measurements, with quantum error correction and without feedback, compared with the best unencoded qubit. The dashed lines indicate the times between which the actively error-corrected logical qubit gives the highest fidelity. The data without feedback (detecting errors without correcting) isolate the suppression of coherently evolving errors by projecting them. For long times, applying error correction lowers the fidelity because the stabilizer measurements extract no useful information about errors, but nevertheless preferentially suppress evolutions that result in phase errors at the end of the sequence (see Supplementary Fig. 10 for a detailed analysis). See Supplementary Fig. 9 for error syndrome probabilities. Solid curves in b,d are fits described in the Methods and Supplementary Notes 1 and 2. Dashed lines are a guide to the eye. All error bars are one statistical s.d.
For a single round of error correction (majority vote only), the average fidelity is higher than for an unencoded qubit for any pe (Fig. 4b); adding more (identical) qubits is always beneficial in the repetition code. For pe=0, additional rounds of quantum error correction can only introduce errors, reducing the fidelity (Fig. 4b). For larger pe, however, multiple rounds prevent errors from accumulating by dividing the error process in parts that are more likely to contain only single errors, which are corrected. In addition, unlike error detection with post processing13,14, active correction between rounds keeps the probability to obtain +1 (no error) high (inset Fig. 4b) and thus maintains the advantage of assigning the highest-fidelity ancilla readout to that outcome. Preventing errors by maximizing the probability that the ancilla qubits reside in the optimal state is a key general advantage of real-time feedback in quantum error correction. As a result, for pe>0.3, multiple rounds outperform a single round of error correction.
Correcting natural dephasing
Finally, as an example of suppressing errors naturally present in the environment, we let the qubits evolve freely instead of applying errors (Fig. 4c). The resulting errors are still spatially uncorrelated across the qubits, but the error probabilities are now different for each qubit because their intrinsic  differ because of their local environments (Fig. 1c). In addition, the errors arise from quasistatic detunings because of the slowly fluctuating 13C spin bath so that the errors in a given experimental run evolve coherently and are correlated in time. Like most environmental errors, such errors might also be suppressed by other methods than quantum error correction, for example, by polarizing the spin environment26,27, by refocusing pulses28 or by isotopic purification28,29,30,31.
differ because of their local environments (Fig. 1c). In addition, the errors arise from quasistatic detunings because of the slowly fluctuating 13C spin bath so that the errors in a given experimental run evolve coherently and are correlated in time. Like most environmental errors, such errors might also be suppressed by other methods than quantum error correction, for example, by polarizing the spin environment26,27, by refocusing pulses28 or by isotopic purification28,29,30,31.
The fidelity for the logical qubit with majority voting again starts above the best unencoded qubit, but drops below it for larger evolution times (Fig. 4d). Because the error probabilities vary between qubits, an error detected on the best qubit becomes more likely to actually correspond to errors on both other qubits and the wrong correction is made. An additional round of quantum error correction in the middle of the evolution time now not only prevents errors from accumulating by intermediately correcting them, but also interrupts any coherent build-up by projecting the errors, thus suppressing them (Fig. 4d). Owing to this combination, the logical qubit shows an enhanced dephasing time (24.2(2) ms against 18.2(9) ms for the best physical qubit) and yields the highest average state fidelity for total evolution times between 5 and 19 ms (Fig. 4d). This result demonstrates an actively error-corrected logical qubit with an improved dephasing time over the best qubit used in the encoding.
Discussion
The presented non-destructive measurements and real-time feedback on encoded quantum states are the key primitives for universal computations on logical qubits and for error-correcting codes that correct both phase and bit-flip errors. To reach scalability thresholds, readout and gate fidelities should be further increased, for example, by: improving the optical collection efficiency through optical cavities32, enhancing coherence times through implantation33 or selective growth of defects and isotopes in purified diamonds28,29, and improving gate design through optimal control33. In a wider perspective, our results can be combined with recently demonstrated entanglement between distant NV centres34,35 to form quantum networks with error-corrected nodes for entanglement purification, quantum communication and networked quantum computation36. Therefore, these results establish a promising platform to experimentally investigate protocols for fault-tolerant quantum information processing under different types of noise and error correlations in diverse settings.
Methods
Sample and setup
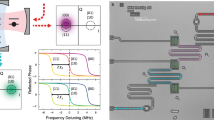
We use a naturally occurring NV in high-purity type IIa chemical-vapour-deposition-grown diamond with a 1.1% natural abundance of 13C and a <111> crystal orientation (Element Six). To enhance the collection efficiency, a solid-immersion lens was fabricated on top of the NV centre17,37 (Fig. 1b) and a single-layer aluminum-oxide anti-reflection coating was deposited34,38. The sample temperature is T≈4.2 K and a magnetic field of 403.553(3) G is applied along the NV symmetry axis.
The ancilla NV electron spin is characterized by a Rabi frequency of 4.3 MHz, a dephasing time  , a Hahn echo time T2=1.03(3) ms and a longitudinal relaxation time of 0.43(6) s (due to microwave noise and laser background). The coherence time of the ancilla under dynamical decoupling exceeds 25 ms and does not limit the experiments (Supplementary Fig. 1). We initialize and readout the ancilla through resonant excitation of the zero-phonon transitions of the NV centre (Supplementary Fig. 2). Before every experiment, the 14N nuclear spin is initialized by measurement with a fidelity of FN=0.94(3) in mI=−1 (ref. 17). No external electric fields are applied: the gates in Fig. 1b are grounded.
, a Hahn echo time T2=1.03(3) ms and a longitudinal relaxation time of 0.43(6) s (due to microwave noise and laser background). The coherence time of the ancilla under dynamical decoupling exceeds 25 ms and does not limit the experiments (Supplementary Fig. 1). We initialize and readout the ancilla through resonant excitation of the zero-phonon transitions of the NV centre (Supplementary Fig. 2). Before every experiment, the 14N nuclear spin is initialized by measurement with a fidelity of FN=0.94(3) in mI=−1 (ref. 17). No external electric fields are applied: the gates in Fig. 1b are grounded.
Nuclear spin qubit control
The hyperfine interactions for the three nuclear spins are estimated by dynamical decoupling spectroscopy9 (Supplementary Table 1). Building on previous gate designs9, nuclear gates are realized by applying sequences of π-pulses on the electron spin of the form (τ−π−2τ−π−τ)N/2. The number of pulses N sets the rotation angle. The inter-pulse delay 2τ determines which qubit is controlled and whether the rotation is conditional on the ancilla state. In contrast to the previous work9, we allow the gates to be detuned, providing greater flexibility to optimize τ and N for gate selectivity and minimal discretization errors. The gate parameters are listed in Supplementary Tables 1 and 2.
The nuclear spins are initialized by swapping with the ancilla electron spin (Supplementary Fig. 3) and are read out by mapping the required correlation to the ancilla before reading it out (Supplementary Fig. 4). To obtain best estimates for the actual states, the results are corrected for the fidelity of the gates used in the final readout (tomography; details in Supplementary Note 3). Uncorrected data are shown in Supplementary Fig. 11.
Feedback
Real-time feedback is implemented through a programmable microprocessor (ADwin Pro II) that controls the experimental sequence (Supplementary Fig. 5). We exploit feedback in four different ways. First, detected phase errors are corrected directly after the stabilizer measurements. Note that analysing errors over multiple rounds14 would additionally enable real-time correction of ancilla readout errors, but that this is not implemented here. Second, depending the ancilla measurement outcome, the qubits pick up a deterministic phase shift due to the hyperfine interaction, which is corrected in the same way. Third, for an odd number of +1 outcomes, the operations in the stabilizer measurements imprint a bit flip on the logical qubit, which we correct by transforming the logical qubit basis in real time. Fourth, to start each measurement sequence with the ancilla in  , it is flipped back to
, it is flipped back to  when the previous measurement returned
when the previous measurement returned  .
.
Importantly, we perform real-time feedback either by adapting the qubit bases for all subsequent gates and measurements (for correcting Z errors and for the logical qubit) or by absorbing the feedback operations into the next gate acting on the same qubit (for the ancilla). Therefore, the physical control sequence is directly adapted based on the measurement outcomes without introducing any unnecessary gate operations that would cause additional errors. In the circuit diagrams, we sometimes display the gates for the feedback separately for clarity.
Quantum error correction analysis
The process fidelity with the identity is given by  , with
, with  , the six fidelities of the final states ρα with the ideal states
, the six fidelities of the final states ρα with the ideal states  . The results of Fig. 3 are analysed by fitting to
. The results of Fig. 3 are analysed by fitting to  , with
, with  and
and  . A and O account for the experimental fidelities (Supplementary Note 1).
. A and O account for the experimental fidelities (Supplementary Note 1).
The state fidelities for multiple rounds of error correction and incoherent errors (Fig. 4b) are fitted to the same equation using  with n the number of rounds, pn the error per round and
with n the number of rounds, pn the error per round and  . The error per round pn is obtained as follows. An error process with total error probability (pe) reduces the expectation value by a factor of (1−2pe). For incoherent errors, a process can be divided in n equal rounds using (1−2pe)=(1−2pn)n, which results in
. The error per round pn is obtained as follows. An error process with total error probability (pe) reduces the expectation value by a factor of (1−2pe). For incoherent errors, a process can be divided in n equal rounds using (1−2pe)=(1−2pn)n, which results in  (for pe≤0.5). In Figs 3c and 4b, A depends on the error-probability pe, because we optimize the effective readout fidelity by associating the most likely error syndrome to the best ancilla readout (Supplementary Note 1). See Supplementary Notes 1 and 2 for further details on all theoretical analysis, including the error syndrome probabilities and numerical simulations of Fig. 4d.
(for pe≤0.5). In Figs 3c and 4b, A depends on the error-probability pe, because we optimize the effective readout fidelity by associating the most likely error syndrome to the best ancilla readout (Supplementary Note 1). See Supplementary Notes 1 and 2 for further details on all theoretical analysis, including the error syndrome probabilities and numerical simulations of Fig. 4d.
Additional information
How to cite this article: Cramer, J. et al. Repeated quantum error correction on a continuously encoded qubit by real-time feedback. Nat. Commun. 7:11526 doi: 10.1038/ncomms11526 (2016).
References
Terhal, B. M. Quantum error correction for quantum memories. Rev. Mod. Phys. 87, 307–346 (2015).
Bravyi, S. B. & Kitaev, A.Y. Quantum codes on a lattice with boundary. Preprint at http://arxiv.org/abs/quant-ph/9811052 (1998).
Raussendorf, R. & Harrington, J. Fault-tolerant quantum computation with high threshold in two dimensions. Phys. Rev. Lett. 98, 190504 (2007).
Nigg, D. et al. Quantum computations on a topologically encoded qubit. Science 345, 302–305 (2014).
Knill, E., Laflamme, R., Martinez, R. & Negrevergne, C. Benchmarking quantum computers: the five-qubit error correcting code. Phys. Rev. Lett. 86, 5811–5814 (2001).
Chiaverini, J. et al. Realization of quantum error correction. Nature 432, 602–605 (2004).
Schindler, P. et al. Experimental repetitive quantum error correction. Science 332, 1059–1061 (2011).
Reed, M. D. et al. Realization of three-qubit quantum error correction with superconducting circuits. Nature 482, 382–385 (2012).
Taminiau, T. H., Cramer, J., van der Sar, T., Dobrovitski, V. V. & Hanson, R. Universal control and error correction in multi-qubit spin registers in diamond. Nat. Nanotech. 9, 171–176 (2014).
Waldherr, G. et al. Quantum error correction in a solid-state hybrid spin register. Nature 506, 204–207 (2014).
Lanyon, B. P. et al. Measurement-based quantum computation with trapped ions. Phys. Rev. Lett. 111, 210501 (2013).
Córcoles, A. D. et al. Demonstration of a quantum error detection code using a square lattice of four superconducting qubits. Nat. Commun 6, 6979 (2015).
Ristè, D. et al. Detecting bit-flip errors in a logical qubit using stabilizer measurements. Nat. Commun 6, 6983 (2015).
Kelly, J. et al. State preservation by repetitive error detection in a superconducting quantum circuit. Nature 519, 66–69 (2015).
Sun, L. et al. Tracking photon jumps with repeated quantum non-demolition parity measurements. Nature 511, 444–448 (2014).
Fuchs, G. D., Dobrovitski, V. V., Toyli, D. M., Heremans, F. J. & Awschalom, D. D. Gigahertz dynamics of a strongly driven single quantum spin. Science 326, 1520–1522 (2009).
Robledo, L. et al. High-fidelity projective read-out of a solid-state spin quantum register. Nature 477, 574–578 (2011).
Bar-Gill, N., Pham, L. M., Jarmola, A., Budker, D. & Walsworth, R. Solid-state electronic spin coherence time approaching one second. Nat. Commun. 4, 1743 (2013).
Liu, G.-Q., Po, H. C., Du, J., Liu, R.-B. & Pan, X.-Y. Noise-resilient quantum evolution steered by dynamical decoupling. Nat. Commun. 4, 2254 (2013).
Jiang, L. et al. Coherence of an optically illuminated single nuclear spin qubit. Phys. Rev. Lett. 100, 073001 (2008).
Pfaff, W. et al. Demonstration of entanglement-by-measurement of solid-state qubits. Nature Phys. 9, 29–33 (2013).
Wolfowicz, G. et al.29Si nuclear spins as a resource for donor spin qubits in silicon. New J. Phys. 18, 023021 (2016).
Blok, M. S. et al. Manipulating a qubit through the backaction of sequential partial measurements and real-time feedback. Nat. Phys. 10, 189–193 (2014).
Barreiro, J. T. et al. An open-system quantum simulator with trapped ions. Nature 470, 486–491 (2011).
Ristè, D. et al. Deterministic entanglement of superconducting qubits by parity measurement and feedback. Nature 502, 350–354 (2013).
London, P. et al. Detecting and polarizing nuclear spins with double resonance on a single electron spin. Phys. Rev. Lett. 111, 067601 (2013).
Shulman, M. D. et al. Suppressing qubit dephasing using real-time Hamiltonian estimation. Nat. Commun. 5, 5156 (2014).
Maurer, P. C. et al. Room-temperature quantum bit memory exceeding one second. Science 336, 1283–1286 (2012).
Balasubramanian, G. et al. Ultralong spin coherence time in isotopically engineered diamond. Nat. Mater 8, 383–387 (2009).
Saeedi, K. et al. Room-temperature quantum bit storage exceeding 39 minutes using ionized donors in silicon-28. Science 342, 830–833 (2013).
Muhonen, J. T. et al. Storing quantum information for 30 seconds in a nanoelectronic device. Nat. Nanotech 9, 986–991 (2014).
Li, L. et al. Coherent spin control of a nanocavity-enhanced qubit in diamond. Nat. Commun. 6, 6173 (2015).
Dolde, F. et al. High-fidelity spin entanglement using optimal control. Nat. Commun. 5, 3371 (2014).
Pfaff, W. et al. Unconditional quantum teleportation between distant solid-state quantum bits. Science 345, 532–535 (2014).
Hensen, B. et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 526, 682–686 (2015).
Nickerson, N. H., Li, Y. & Benjamin, S. C. Topological quantum computing with a very noisy network and local error rates approaching one percent. Nat. Commun. 4, 1756 (2013).
Hadden, J. P. et al. Strongly enhanced photon collection from diamond defect centres under microfabricated integrated solid immersion lenses. Appl. Phys. Lett. 97, 241901 (2010).
Yeung, T. K. et al. Anti-reflection coating for nitrogen-vacancy optical measurements in diamond. Appl. Phys. Lett. 100, 251111 (2012).
Acknowledgements
We thank L. Dicarlo, L.M.K. Vandersypen, A.G. Fowler and V.V. Dobrovitski for discussions and comments. We acknowledge support from the Dutch Organization for Fundamental Research on Matter (FOM), the Netherlands Organization for Scientific Research (NWO), the Defense Advanced Research Projects Agency QuASAR program and the European Research Council through a Starting Grant. T.H.T. is supported by an NWO VENI grant.
Author information
Authors and Affiliations
Contributions
J.C., R.H. and T.H.T. devised the experiments. J.C., N.K., M.A.R., B.H., M.S.B. and T.H.T. prepared the experimental apparatus. M.M. and D.J.T. grew the diamond. J.C. and T.H.T. performed the experiments. J.C., N.K. and T.H.T. analysed the data with help of all authors. T.H.T. supervised the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-11, Supplementary Tables 1-2, Supplementary Notes 1-3 and Supplementary References (PDF 5199 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Cramer, J., Kalb, N., Rol, M. et al. Repeated quantum error correction on a continuously encoded qubit by real-time feedback. Nat Commun 7, 11526 (2016). https://doi.org/10.1038/ncomms11526
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms11526
This article is cited by
-
A quantum router architecture for high-fidelity entanglement flows in quantum networks
npj Quantum Information (2022)
-
Experimental demonstration of continuous quantum error correction
Nature Communications (2022)
-
Fault-tolerant operation of a logical qubit in a diamond quantum processor
Nature (2022)
-
Logical-qubit operations in an error-detecting surface code
Nature Physics (2022)
-
Qubit teleportation between non-neighbouring nodes in a quantum network
Nature (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.