Abstract
The ability to exfoliate layered materials down to the single layer limit has presented the opportunity to understand how a gradual reduction in dimensionality affects the properties of bulk materials. Here we use this top–down approach to address the problem of superconductivity in the two-dimensional limit. The transport properties of electronic devices based on 2H tantalum disulfide flakes of different thicknesses are presented. We observe that superconductivity persists down to the thinnest layer investigated (3.5 nm), and interestingly, we find a pronounced enhancement in the critical temperature from 0.5 to 2.2 K as the layers are thinned down. In addition, we propose a tight-binding model, which allows us to attribute this phenomenon to an enhancement of the effective electron–phonon coupling constant. This work provides evidence that reducing the dimensionality can strengthen superconductivity as opposed to the weakening effect that has been reported in other 2D materials so far.
Similar content being viewed by others
Introduction
The behaviour of superconductors in the two-dimensional (2D) limit is a long-standing problem in physics that has been the focus of extensive research in the field1,2,3,4,5,6. The bottom–up approach has provided signs of the existence of superconductivity at the 2D limit in experiments performed on in situ-grown, ultrathin lead films fabricated by evaporation7,8. However, for films grown in this way, it is difficult to avoid the strong influence from the substrate lattice, yielding typically highly disordered films. A different approach takes advantage of the ability of certain van der Waals materials to be separated into individual layers, which may later be isolated as defect-free 2D crystals on a substrate of choice9. This top–down approach permits overcoming the lattice and chemical restrictions imposed by the substrate in the bottom–up strategy in such a way that the coupling may be minimized by an appropriate choice of surface10,11,12.
Although graphene is not an intrinsic superconductor, recent studies have brought forward the possibility of inducing superconductivity in this 2D material by garnishing its surface with the right species of dopant atoms or, alternatively, by using ionic liquid gating13,14. However, reported experiments have failed to show direct evidence of superconducting behaviour in exfoliated graphene, leaving out the archetypal material from studies of 2D superconductivity15.
An even more attractive family of 2D materials is provided by the transition metal dichalcogenides (TMDCs) since some of its members exhibit superconductivity in the bulk state16,17. Just as in graphene, TMDCs present a strong in-plane covalency and weak interlayer van der Waals interactions, which allow exfoliation of the bulk18. This has given rise to a very rich chemistry of hybrid multifunctional materials based on the restacking of TMDC nano-layer sols with functional counterparts19,20. In addition, the all-dry exfoliation methodologies have allowed for the deposition of TMDC flakes on a variety of surfaces21,22. These micromechanical exfoliation techniques allow access to nearly defect-free, large surface area flakes of virtually any TMDC, opening the door to the study of how a dimensionality reduction affects the properties of these materials23,24,25,26. Surprisingly, despite the works reported in the literature searching for intrinsic superconductivity in atomically thin 2D crystals27,28,29, for a long time the sole examples came from FeSe thin films grown in situ on a substrate30,31,32,33. Only very recently, several studies of niobium diselenide (NbSe2) flakes have yielded the first clear evidence of the existence of superconductivity in freshly cleaved specimens of less than three layers in thickness34,35,36,37.
Tantalum disulphide (TaS2) is another member of the TMDC family. In its bulk state, TaS2 is composed of robust covalently bonded S–Ta–S planes that stack upon each other. A variety of polytypic phases originate from the distinct in-plane Ta coordination spheres described by the S2− ligands and by the stacking periodicity of the individual planes. For instance, the 2H and 1T polytypes present unit cells with two trigonal bipyramidal and one octahedral Ta-coordinated layers, respectively. Although extensively explored in the 1960s38, 1T and 2H polytypes are once again attracting major attention as they constitute ideal case studies for the investigation of competing orders, namely, superconductivity, charge density waves (CDW)39,40 and hidden phases41. In this scenario, the study of decoupled or isolated TaS2 layers may provide new insights into these exotic phenomena42. Transport measurements of few-layer TaS2 flakes have been reported in flakes as thin as 2 nm, but superconductivity in TaS2 layers thinner than 8 nm has not been observed, probably due to the environmental degradation of the samples43.
Here, we explore 2D superconductivity in few-molecular-layer tantalum disulphide flakes of different thicknesses, which have been mechanically exfoliated onto Si/SiO2 substrates. Interestingly, we observe that superconductivity persists down to the thinnest layer investigated (3.5 nm, approximately 5 covalent planes), with a pronounced increase in the critical temperature (Tc) from 0.5 K (bulk crystal) to ∼2.2 K when the thickness of the layer is decreased. In search of the origin of these observations, we perform density functional theory (DFT) calculations and construct a simple tight binding model to study the change in the electronic band structure and density of states (DOSs) at the Fermi level as a function of reduced thickness. We ascribe the enhancement to an increase in the effective coupling constant (λeff) for reduced thicknesses, which ultimately determines Tc.
Results
Fabrication of transport devices
Although the exfoliation of other TMDC members has been extensively studied, little has been reported on the controlled isolation of atomically thin 2H-TaS2 flakes. This layered material appears to be difficult to exfoliate and is also particularly susceptible to oxidation in atmospheric conditions44, hindering the manipulation of very thin flakes in open moist air. Although complex encapsulation techniques help preserving samples from oxidation36, we find that a rapid integration of freshly exfoliated flakes into final devices and their immediate transfer to vacuum conditions for measurement also permits retaining the pristine properties of most TaS2 samples (vide infra).
The experimental process begins with the chemical vapour transport growth of bulk TaS2 crystals (vide infra in Methods), which are subsequently exfoliated onto Si/SiO2 substrates. To ensure a high-quality material, optical, Raman and atomic force microscopy characterization were performed on exfoliated flakes of varying thicknesses (see Supplementary Figs 1–5 and Supplementary Note 1 and 2 for details). As already established for graphene and other TMDCs, inspection of the substrate surface by optical microscopy permits identifying the presence of nanometre thin TaS2 flakes. In an attempt to access flakes with a reduced number of atomic layers, we developed a modification of the micromechanical exfoliation method and optimized it for the controlled isolation of few-layer 2H-TaS2 flakes45,46. The method relies on precisely controlling a uniaxial pressure applied directly with a single crystal over the accepting substrate and in combination with a shearing cleavage movement. This allows for the cleavage of very thin flakes, down to 1.2 nm thick (see Supplementary Fig. 1 for details), corresponding to a single 2H-TaS2 unit-cell (see Fig. 1a) formed by two individual layers. Unfortunately, all attempts to contact these flakes and measure transport properties were unsuccessful, likely due to their instability in ambient conditions.
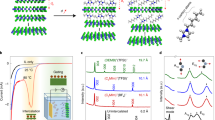
(a) Ball and stick model of the crystal structure of the 2H polytype of TaS2. The dashed prism encloses the content of a single unit cell and the metal coordination geometry is highlighted by the red polyhedron. (b) Atomic force microscopy image of two devices fabricated on a 3.5-nm 2H-TaS2 flake. The scale bar is 4 μm in length. The full colour scale of the topograph corresponds to a height of 100 nm. (c) Line profile of the flake taken at the location of the white dotted line in b.
To avoid the oxidation of few layer flakes, freshly exfoliated samples designated for device fabrication and transport measurements are immediately covered with an methyl methacrylate/poly (methyl methacrylate) double layer resist in preparation for subsequent device nanofabrication steps. Figure 1b shows an example of a fabricated device incorporating the thinnest flake measured with a thickness of 3.5 nm (corresponding to approximately 5 layers) and lateral dimensions of the order of a few micrometres as imaged by atomic force microscopy. The chromium/gold (Cr/Au, 5 nm/70 nm) electrodes were evaporated onto selected flakes by employing standard e-beam lithography techniques (see Methods for details). All transport measurements were made using a four terminal current bias configuration in a temperature range of 20 mK to 4 K in a dilution fridge.
Transport properties and superconductivity
We present measurements on 12 flakes of varying thicknesses in the ≈3–30 nm range, integrated in the described four-terminal devices, with the aim of studying the effect of dimensionality reduction on the superconducting properties of TaS2. All devices show a superconducting transition observed by four terminal current bias measurements as a function of temperature. Figure 2 shows the current–voltage (I–V) and resistance–temperature (R–T) characteristics for three representative devices having thicknesses of 14.9 nm (Fig. 2a,b), 5.8 nm (Fig. 2c,d) and 4.2 nm (Fig. 2e,f). The transport data for the thinnest 3.5 nm flake can be found in the Supplementary Fig. 6. The zero bias, numerical derivatives (dV/dI) as a function of temperature show a clear superconducting transition for each device (Fig. 2b,d,f). From these (interpolated) curves, we estimate Tc, taken at 50% of the normal-state resistance. For the 14.9 nm flake, and despite the fact that the sample does not attain a zero resistive state, one may still appreciate that there is a phase transition centred at 540±230 mK. This is in rough agreement with previously reported Tc values of 600 mK for bulk 2H-TaS2 material47. Interestingly, and in contrast with studies on other 2D superconductors, the Tc values show a marked increase for the thinner flakes of 5.8 nm (1.45±0.13 K) and 4.2 nm (1.79±0.20 K). This peculiar result is discussed in detail below. In addition, critical current densities increase by orders of magnitude as the devices become thinner (14.9 nm, Jc≈700 A cm−2, 5.8 nm, Jc≈7 × 104 A cm−2 and 4.2 nm, Jc≈5 × 105 A cm−2). In thin film superconductors with high critical current densities, as those measured in our thinnest flakes, Joule self-heating starts to play a role48. This explains the pronounced asymmetry in the I–V characteristics for thinner flakes (Fig. 2a versus Fig. 2e). As the current bias is swept from high negative values through zero, non-equilibrium Joule heating pushes the superconducting transition to a lower current value. This asymmetry decreases as the temperature approaches Tc, where Joule heating effects become less significant (Fig. 2e).
Temperature dependence of three selected devices spanning the range of thicknesses studied. (a) Current–voltage (I–V) characteristics as a function of temperature for a bulk-like 14.9 nm device. (b) Resistance (zero bias numerical derivative) versus temperature for the 14.9 nm device. (c) I–V characteristics as a function of temperature for a 5.8-nm device. (d) Resistance versus temperature for the 5.8-nm device. (e) I–V characteristics as a function of temperature for a 4.2-nm device. (f) Resistance versus temperature for the 4.2-nm device.
Effect of an external magnetic field on superconductivity
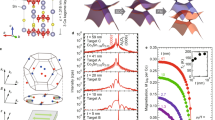
To further characterize the devices at 50 mK, the upper critical field (Bc2) of these type II superconductors is determined by applying an external magnetic field, perpendicular to the surface of the flake. Figure 3 shows colour scale plots of dI/dV–I curves as a function of external field for the same three devices as in Fig. 2. Figure 3b shows the zero-bias differential resistance as a function of external field. From these curves, we estimate the Bc2 as the external field at which the device returns to the normal-state resistance. Once again, in accordance with the upper critical field reported for the bulk material (110 mT), we measure a Bc2 of ≈130 mT for the bulk-like 14.9 nm flake49. The thinner flakes present higher upper critical fields of ≈0.9 T (5.8 nm) and ≈1.7 T (4.2 nm) following the interesting trend for Tc. The critical fields at 50 mK allow estimation of the superconducting Ginzburg–Landau coherence lengths given by: Bc2(50 mK)=ϕ0/2πξ(50 mK) (ref. 2). The coherence lengths for the 4.2 and 5.8 nm flakes are 13.9 and 19.1 nm, respectively, suggesting that these flakes are in the 2D limit. To further qualify the 2D nature of the thinnest flakes, we analyse the I–V and R–T curves (such as those in Fig. 2) of selected devices at zero external field in order to infer the typical signature of 2D superconductivity: the Berezinskii–Kosterlitz–Thouless transition (see Supplementary Fig. 7 and Supplementary Note 3 for details). Note that this study can only be carried out for selected thinner samples for which sufficient data are available. We find that the transport data are consistent with a Berezinskii–Kosterlitz–Thouless superconducting transition, further supporting the 2D nature of the thinnest TaS2 flakes.
Perpendicular external magnetic field dependence at 30 mK for three selected devices spanning the range of thicknesses studied. (a) Resistance (zero bias numerical derivative) versus applied field for a bulk-like, 14.9 nm device. (b) Zero bias resistance versus applied field for the 14.9-nm device. (c) Resistance (zero bias numerical derivative) versus applied field for the 5.8-nm device. (d) Zero bias resistance versus applied field for the 5.8-nm device. (e) Resistance versus applied field for the 4.2-nm device. (f) Zero bias resistance versus applied field for the 4.2-nm device.
Effect of dimensionality on the superconducting state
We now turn our attention to the collective behaviour of our 12 devices and the effect of reduced dimensionality on the superconducting properties of TaS2. Figure 4 illustrates the measured Tc and Bc2 for the devices reported. A bulk limit was found for samples over 10 nm in thickness, such as the one in Figs 2a,b and 3a,b, for which the superconducting properties were consistent with bulk crystals and did not depend on the number of layers. It is interesting to note that these types of flakes exhibit a non-zero residual resistance (red data points) at base temperature, indicating a certain degree of crystalline inhomogeneity and providing a plausible explanation to the slight variation of Tc, similar to the variation in reported bulk values (0.6 and 0.8 K) (refs 25, 50). The bulk-limit devices approach the edge of the 2D limit set by the Ginzburg-Landau (GL) coherence length (ξ=55 nm) estimated from the bulk Bc2 (see Fig. 4b).
(a) Variation of Tc as a function of the thickness of the TaS2 flakes. Devices exhibiting a non-zero residual resistance below Tc are plotted in red. The error bars are given by the temperatures at 10 and 90% of the normal state resistance. The solid black line marks the bulk Tc of 600 mK. The black dotted line is an exponential trend line, fit to the data starting at the bulk limit. (b) Variation of Bc2 as a function of flake thickness. The red circles mark the same devices in a having residual resistance. The black solid line indicates the bulk limit upper critical field of 110 mT. The grey solid line plots the GL coherence lengths, calculated from the y axis Bc2 values, and marks the edge of the 2D limit.
Discussion
In addition to thicker flakes that behave in a way consistent with bulk properties, we also observe the superconducting transition in devices made out of thinner TaS2 flakes, down to 3.5 nm (∼5 layers). Interestingly, we observe a strong enhancement of Tc and Bc2 for thinner flakes, up to more than a factor of four larger than in the bulk material. The Tc enhancement with decreasing number of layers exhibited by the TaS2 samples is in strict contrast to the Tc suppression previously reported in elemental materials7, binary systems51 and even the closely related dichalcogenide family member, NbSe2 (ref. 29). A common theme in these studies is that as the material is thinned down, substrate interactions, either from induced strain or increased Coulomb interactions, suppress the formation of Cooper pairs. In NbSe2 devices, a clear correspondence can be made with a decrease in the residual resistance ratio (RRR) giving an indication of increased substrate interactions or more probable that flake degradation is more prevalent in thinner flakes30. This agrees with our attempts to contact flakes thinner than 3.5 nm showing a complete insulating state at room temperature. Correspondingly, the RRR values (see Supplementary Fig. 8 for details) for our TaS2 sample set show a significant reduction for the two thinnest flakes. However, devices as thin as 4.5 nm still maintain an RRR of 10, indicating pristine thin samples even below our bulk limit of 10 nm.
An initial point that needs to be addressed once trying to interpret the Tc enhancement is the possibility of electrochemical doping coming from either the original crystals, or through fabrication processes (lithography resists). Although it is well understood that the Tc of TaS2 crystals is particularly sensitive to intrinsic non-stoichiometric doping52, we may rule out this effect coming from the original crystals by having measured a bulk Tc of ∼0.5 K. Now considering the potential doping coming from environmental or intercalation interactions, Raman spectroscopy provides us with strong evidence of the absence of such processes. In contrast with the remarkable peak shifts displayed by intercalated crystals of 2H-MX2 (ref. 53), the Raman spectra of exfoliated flakes presented in the supplement (review Supplementary Figs 3–5) show no significant change in crystal structure for flakes of only four layers. Given that the flakes are not undergoing intercalation through exfoliation or fabrication, there could indeed be some doping coming from surface contamination or from the oxide substrate. However, previous studies show that gate-induced or surface-induced electrostatic doping allows for a carrier density modulation of maximum ca 1012 cm−2 (ref. 54), which is at least three orders of magnitude lower than the estimated single-layer carrier concentration in these metallic TMDCs (ca 1015 cm−2) (refs 30, 55). In this line, these doping effects have shown to modulate Tc in NbSe2 by 8% at most30. Finally, although substrate interactions have led to the interesting Tc enhancements found in epitaxial grown FeSe on STO, we rule out such effects as the TaS2 flakes presented here are weakly coupled to the substrate. This suggests a deeper mechanism as opposed to simple substrate interaction, intercalation or degradation reported in previous studies.
A possible mechanism at work could be the enhancement of the superconducting properties associated with a suppression of the commensurate CDW order, which is in direct competition with superconducting pairing19. This is consistent with the interpretation presented of the enhanced Tc and Bc2 observed in the studies of intercalation of TMDC, where it is argued that the in-plane chemical doping leads to the suppression of the charge density order, and in certain TMDCs under pressure where the same claim is made49,56,57. To explore the effect of the CDW on the DOS at the Fermi level as a function of reduced thickness, we calculate the DOS from an effective one-orbital tight-binding model and simulate the CDW at a mean field level as a periodic potential that locally shifts the onsite energy (see Supplementary Figs 9 and 10 and Supplementary Note 4 for details). We find that the DOS at the Fermi level is not appreciably affected by the CDW for reduced thicknesses. Ultimately, to determine if such a competition with CDWs could be playing a role, one could search for direct evidence of such suppression in STM studies of thin flakes below the 10-nm bulk limit observed here.
An alternative explanation of the enhanced Tc could be a change of the band structure of the material in atomically thin flakes. To explore this possibility, we perform DFT calculations and construct a simplified tight-binding model to study the electronic band structure and DOS νN(0) as a function of the sample thickness. The results of the calculation can be observed in the Supplementary Figs 11 and 12 and Supplementary Notes 5 and 6. The resulting 2D bands contain hole pockets and show saddle points below the Fermi level. These saddle points give rise to van Hove peaks, whose height increases as the number of layers is decreased, and ultimately diverge in the 2D limit. However, the DOS per layer at the Fermi level νN(0) decreases as the number of layer is reduced (see Supplementary Fig. 13 for details). For a simplified model with a constant attractive interaction V, the coupling constant, that ultimately determines the Tc, takes the usual BCS value λ=VνN(0). This behaviour of the DOS would suggest at first an analogous trend of Tc, which does not suffice to explain the experiments. The value of the superconducting gap and Tc can be influenced by the interactions properties of the material. The effective coupling constant58 determining Tc is given by λeff=λ–μ*, where λ is the electron–phonon coupling constant, and μ*, known as Anderson–Morel pseudo-potential, is a term that represents the renormalized repulsive Coulomb interaction. In usual 3D superconductors characterized by a featureless—hence constant—DOS, the projection on the Fermi level of the high-energy degrees of freedom gives rise to a pseudo-potential of the form μ*=μ/(1+μ ln(W/ω0)), with ω0 the characteristic phonon frequency, W the system bandwidth and μ the bare Coulomb repulsion. In a 2D system, with a DOS characterized by a van Hove singularity near the Fermi level, the renormalization of the bare μ can be significantly larger than in a 3D material. This effect is therefore strongly dependent on the number of layers. For a generic DOS νN(ɛ), the pseudo-potential takes the form

with  the total DOS normalized with its value at the Fermi energy. Assuming a constant repulsive interaction U, one can estimate μ=UνN(0). For a weak repulsion, the renormalization is negligible and the effective coupling constant follows the DOS at the Fermi level νN(0). For a relatively strong Coulomb repulsion, the value of the pseudo-potential at the Fermi level can be strongly affected by features of the DOS at higher energies, such as van Hove singularities. As the number of layers is decreased, the renormalization of a relatively strong repulsion for the band structure in the model is sufficient to reverse the dependence of Tc on the number of layers obtained from a simple electron–phonon attractive interaction (see Supplementary Fig. 14 for details). This analysis points to a non-negligible role of the Coulomb repulsive interaction in superconducting 2H-TaS2, characterized by a predominant Ta 5d orbital character at the Fermi level. The Coulomb repulsion has also been proposed to be at the origin of superconductivity in MoS2 (refs 59, 60, 61).
the total DOS normalized with its value at the Fermi energy. Assuming a constant repulsive interaction U, one can estimate μ=UνN(0). For a weak repulsion, the renormalization is negligible and the effective coupling constant follows the DOS at the Fermi level νN(0). For a relatively strong Coulomb repulsion, the value of the pseudo-potential at the Fermi level can be strongly affected by features of the DOS at higher energies, such as van Hove singularities. As the number of layers is decreased, the renormalization of a relatively strong repulsion for the band structure in the model is sufficient to reverse the dependence of Tc on the number of layers obtained from a simple electron–phonon attractive interaction (see Supplementary Fig. 14 for details). This analysis points to a non-negligible role of the Coulomb repulsive interaction in superconducting 2H-TaS2, characterized by a predominant Ta 5d orbital character at the Fermi level. The Coulomb repulsion has also been proposed to be at the origin of superconductivity in MoS2 (refs 59, 60, 61).
In conclusion, we have reported 2D superconductivity in 2H-TaS2 in atomically thin layers. In contrast to other van der Waals superconductors such as NbSe2, we find that the Tc of this material is strongly enhanced from the bulk value as the thickness is decreased. In addition to a possible charge-density wave origin, we propose a model in which this enhancement arises from an enhancement of the effective coupling constant, which determines the Tc. Our results provide evidence of an unusual effect of the reduction of dimensionality on the properties of a superconducting 2D crystal and unveil another aspect of the exotic manifestation of superconductivity in atomically thin transition metal dichalcogenides.
Methods
Crystal growth
Polycrystalline 2H-TaS2 was synthesized by heating stoichiometric quantities of Ta and S in an evacuated quartz ampoule at 900 °C for 9 days. The growth of large single crystals from the polycrystalline sample was achieved by employing a three-zone furnace. The powder sample was placed in the leftmost zone of the furnace and the other two zones were initially brought to 875 °C and kept at that temperature for 1 day. Following, the temperature of the source zone was risen to 800 °C during the course of 3 h. The temperature of the centre zone was then gradually cooled down at a speed of 1 °C min−1 until a gradient of 125 °C was finally established between the leftmost (875 °C) and centre (750 °C) zones. A gradient of 50 °C was also set between the rightmost and growth zones. This temperature gradient was maintained for 120 h and the furnace was then switched off and left to cool down naturally. The crystals were then thoroughly rinsed with diethyl ether and stored under an N2 atmosphere.
Device fabrication
Contact pads and optical markers are first created on the surface of the Si/SiO2 substrates to locate and design contacts to the transferred flakes. The contacts (chromium−5 nm/ gold−70 nm) are then patterned with standard e-beam lithography (Vistec, EBPG5000PLUS HR 100), metal deposition (AJA International) and subsequent lift-off in warm acetone. To preserve the sample integrity, it is crucial to exfoliate, pattern the electrodes and load into the dilution fridge within a few hours. In that respect and even after minimizing the fabrication time, all attempts to contact flakes with thicknesses below 3.5 nm were unsuccessful because of sample degradation.
Band structure calculations
The DFT simulation of the band structure of 2H-TaS2 has been performed using the Siesta code on systems with different number of layers62. We use the generalized gradient approximation, in particular, the functional of Perdew, Burke and Ernzerhoff63. In addition, we use a split-valence double-ζ basis set including polarization functions64. The energy cutoff of the real space integration mesh was set to 300 Ry and the Brillouin zone k sampling was set, within the Monkhorst–Pack scheme65, to 30 × 30 × 1 in the case of multi-layer samples and 30 × 30 × 30 in the case of the bulk calculation. We use the experimental crystal structure of 2H-TaS2 for all the calculations66.
Additional information
How to cite this article: Navarro-Moratalla, E. et al. Enhanced superconductivity in atomically thin TaS2. Nat. Commun. 7:11043 doi: 10.1038/ncomms11043 (2016).
References
Beasley, M. R., Mooij, J. E. & Orlando, T. P. Possibility of vortex-antivortex pair dissociation in two-dimensional superconductors. Phys. Rev. Lett. 42, 1165–1168 (1979).
Haviland, D. B., Liu, Y. & Goldman, A. M. Onset of superconductivity in the two-dimensional limit. Phys. Rev. Lett. 62, 2180–2183 (1989).
Yazdani, A. & Kapitulnik, A. Superconducting-insulating transition in two-dimensional α-MoGe thin films. Phys. Rev. Lett. 74, 3037–3040 (1995).
Goldman, A. M. & Markovic, N. Superconductor-insulator transitions in the two-dimensional limit. Phys. Today 11, 39–44 (1998).
Guo, Y. et al. Superconductivity modulated by quantum size effects. Science 306, 1915–1917 (2004).
Hermele, M., Refael, G., Fisher, M. P. A. & Goldbart, P. M. Fate of the Josephson effect in thin-film superconductors. Nat. Phys 1, 117–121 (2005).
Qin, S., Kim, J., Niu, Q. & Shih, C. K. Superconductivity at the two-dimensional limit. Science 324, 1314–1317 (2009).
Zhang, T. et al. Superconductivity in one-atomic-layer metal films grown on Si(111). Nat. Phys. 6, 104–108 (2010).
Novoselov, K. S. et al. Two-dimensional atomic crystals. Proc. Natl Acad. Sci. USA 102, 10451–10453 (2005).
Dean, C. R. et al. Boron nitride substrates for high-quality graphene electronics. Nat. Nanotechnol. 5, 722–726 (2010).
Zhou, S. Y. et al. Substrate-induced bandgap opening in epitaxial graphene. Nat. Mater. 6, 770–775 (2007).
Romero-Bermúdez, A. & García-García, A. M. Size effects in superconducting thin films coupled to a substrate. Phys. Rev. B 89, 064508 (2014).
Profeta, G., Calandra, M. & Mauri, F. Phonon-mediated superconductivity in graphene by lithium deposition. Nat. Phys. 8, 131–134 (2012).
Nandkishore, R., Levitov, L. S. & Chubukov, A. V. Chiral superconductivity from repulsive interactions in doped graphene. Nat. Phys. 8, 158–163 (2012).
Uesugi, E., Goto, H., Eguchi, R., Fujiwara, A. & Kubozono, Y. Electric double-layer capacitance between an ionic liquid and few-layer graphene. Sci. Rep. 3, 1595 (2013).
Wilson, J. A. & Yoffe, A. D. The transition metal dichalcogenides discussion and interpretation of the observed optical, electrical and structural properties. Adv. Phys. 18, 193–335 (1969).
Friend, R. & Yoffe, A. Electronic properties of intercalation complexes of the transition metal dichalcogenides. Adv. Phys. 36, 1–94 (1987).
Cunningham, G. et al. Solvent exfoliation of transition metal dichalcogenides: dispersibility of exfoliated nanosheets varies only weakly between compounds. ACS Nano 6, 3468–3480 (2012).
Coronado, E., Martí-Gastaldo, C., Navarro-Moratalla, E., Ribera, A., Blundell, S. & Baker, P. Coexistence of superconductivity and magnetism by chemical design. Nat. Chem. 2, 1031–1036 (2010).
Coronado, E., Martí-Gastaldo, C., Navarro-Moratalla, E., Burzurí, E., Camón, A. & Luis, F. Hybrid magnetic/superconducting materials obtained by insertion of a single-molecule magnet into TaS2 layers. Adv. Mater. 23, 5021–5026 (2011).
Novoselov, K. S. et al. Two-dimensional atomic crystals. Proc. Natl Acad. Sci. USA 102, 10451–10453 (2005).
Meitl, M. A. et al. Transfer printing by kinetic control of adhesion to an elastomeric stamp. Nat. Mater. 5, 33–38 (2005).
Lee, C. et al. Frictional characteristics of atomically thin sheets. Science 328, 76–80 (2010).
Mak, K., Lee, C., Hone, J., Shan, J. & Heinz, T. Atomically thin MoS2: a new direct-gap semiconductor. Phys. Rev. Lett. 105, 136805 (2010).
Splendiani, A. et al. Emerging photoluminescence in monolayer MoS2. Nano Lett. 10, 1271–1275 (2010).
Chiritescu, C. et al. Ultralow thermal conductivity in disordered, layered WSe2 crystals. Science 315, 351–353 (2007).
Frindt, R. Superconductivity in ultrathin NbSe2 Layers. Phys. Rev. Lett. 28, 299–301 (1972).
Staley, N., Wu, J., Eklund, P., Liu, Y., Li, L. & Xu, Z. Electric field effect on superconductivity in atomically thin flakes of NbSe2 . Phys. Rev. B 80, 184505 (2009).
El-Bana, M. S., Wolverson, D., Russo, S., Balakrishnan, G., Paul, D. M. & Bending, S. J. Superconductivity in two-dimensional NbSe2 field effect transistors. Superconductor Sci. Technol. 26, 125020 (2013).
Li, Q., Si, W. & Dimitrov, I. K. Films of iron chalcogenide superconductors. Rep. Prog. Phys 74, 124510 (2011).
Liu, D. et al. Electronic origin of high-temperature superconductivity in single-layer FeSe superconductor. Nat. Commun. 3, 931–937 (2012).
He, S. et al. Phase diagram and electronic indication of high-temperature superconductivity at 65 K in single-layer FeSe films. Nat. Mater. 12, 605–610 (2013).
Yu, R., Goswami, P., Nikolic, P., Zhu, J.-X. & Si, Q. Superconductivity at the border of electron localization and itinerancy. Nat. Commun. 4, 2783 (2013).
Cao, Y. et al. Quality heterostructures from two dimensional crystals unstable in air by their assembly in inert atmosphere. Nano Lett. 15, 4914–4921 (2015).
Xi, X. et al. Strongly enhanced charge-density-wave order in monolayer NbSe2 . Nat. Nanotechnol 10, 1–6 (2015).
Xi, X. et al. Ising pairing in superconducting NbSe2 atomic layers. Nat. Phys. 12, 139–143 (2015).
Tsen, A. W. et al. Nature of the quantum metal in a two-dimensional crystalline superconductor. Nat. Phys doi:10.1038/nphys3579 (2015).
Jellinek, F. The system tantalum-sulfur. J. Less-Common Metals 4, 9–15 (1962).
Castro Neto, A. H. Charge density wave, superconductivity, and anomalous metallic behavior in 2D transition metal dichalcogenides. Phys. Rev. Lett. 86, 4382–4385 (2001).
Guillamón, I. et al. Chiral charge order in the superconductor 2H-TaS2 . N. J. Phys. 13, 103020 (2011).
Stojchevska, L. et al. Ultrafast switching to a stable hidden quantum state in an electronic crystal. Science 344, 177–180 (2014).
Galvis, J. A. et al. Zero-bias conductance peak in detached flakes of superconducting 2H-TaS2 probed by scanning tunneling spectroscopy. Phys. Rev. B 89, 224512 (2014).
Ayari, A., Cobas, E., Ogundadegbe, O. & Fuhrer, M. S. Realization and electrical characterization of ultrathin crystals of layered transition-metal dichalcogenides. J. Appl. Phys. 101, 014507 (2007).
Greenwood, N. N. & Earnshaw, A. Chemistry of the Elements Elsevier Butterworth-Heinemann (1997).
Navarro-Moratalla, E. Two-Dimensional Materials: from Hybrid Magnetic Multilayers to Superconducting Single Layers PhD thesis Universitat de Valencia (2013).
Navarro-Moratalla, E., Pinilla-Cienfuegos, E. & Coronado, E. Método y sistema de exfoliación micromecánica por vía seca de materiales laminares bidimensionales. Spanish Patent number P201300252 (2013).
Garoche, P., Manuel, P., Veyssie, J. J. & Molinié, P. Dynamic measurements of the low-temperature specific heat of 2H—TaS2 single crystals in magnetic fields. J Low Temp. Phys. 30, 323–336 (1978).
Gurevich, A. V. & Mints, R. G. Self-heating in normal metals and superconductors. Rev. Modern Phys. 59, 941–999 (1987).
Vicent, J., Hillenius, S. & Coleman, R. Critical-field enhancement and reduced dimensionality in superconducting layer compounds. Phys. Rev. Lett. 44, 892–895 (1980).
Di Salvo, F. J., Schwall, R., Geballe, T. H., Gamble, F. R. & Osiecki, J. H. Superconductivity in Layered Compounds with Variable Interlayer Spacings. Phys. Rev. Lett. 27, 310–313 (1971).
Kang, L. et al. Suppression of superconductivity in epitaxial NbN ultrathin films. J. Appl. Phys. 109, 033908 (2011).
Wagner, K. E. et al. Tuning the charge density wave and superconductivity in CuxTaS2 . Phys. Rev. B 78, 104520 (2008).
Hangyo, M., Shin-Ichi, N. & Akiyoshi, M. Raman spectroscopic studies of MX2-type layered compounds. Ferroelectrics 52, 151–159 (1983).
Zhang, Y., Tan, Y.-W., Stormer, H. L. & Kim, P. Experimental observation of the quantum Hall effect and Berry's phase in graphene. Nature 438, 201–204 (2005).
Naito, M. & Tanaka, S. Electrical transport properties in 2H-NbS2, -NbSe2, -TaS2 and -TaSe2 . J. Phys. Soc. Jpn 51, 219–227 (1982).
Biberacher, W., Lerf, A., Buheitel, F., Butz, T. & Hubler, A. On the preparation and characterization of ‘NaOH.TaS2’. Mater. Res. Bull. 17, 633–640 (1982).
Feng, Y. et al. Order parameter fluctuations at a buried quantum critical point. Proc. Natl Acad. Sci. USA 109, 7224–7229 (2012).
Anderson, P. W. & Morel, P. Calculation of the superconducting state parameters with retarded electron-phonon interaction. Phys. Rev 125, 1263–1271 (1962).
Taniguchi, K., Matsumoto, A., Shimotani, H. & Takagi, H. Electric-field-induced superconductivity at 9.4 K in a layered transition metal disulphide MoS2 . Appl. Phys. Lett. 101, 042603 (2012).
Ye, J. T. et al. Superconducting dome in a gate-tuned band insulator. Science 338, 1193 (2012).
Roldan, R., Cappelluti, E. & Guinea, F. Interactions and superconductivity in heavily doped MoS2 . Phys. Rev. B 88, 054515 (2013).
Soler, J. M. et al. The SIESTA method for ab initio order-N materials simulation. J. Phys. Condens. Matter. 14, 2745–2779 (2002).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Artacho, E., Sánchez-Portal, D., Ordejón, P., García, A. & Soler, J. M. Linear-scaling ab-initio calculations for large and complex systems. Phys. Stat. Sol. (b) 215, 809–817 (1999).
Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976).
Meetsma, A., Wiegers, G. A., Haange, R. J. & de Boer, J. L. Structure of 2H-TaS2 . Acta Crystallogr. C: Crystal Struct. Commun. 46, 1598–1599 (1990).
Acknowledgements
Financial support from the EU (ELFOS project and ERC Advanced Grant SPINMOL), the Spanish MINECO (Excellence Unit “María de Maeztu” MDM-2015-0538, Project Consolider-Ingenio in Molecular Nanoscience and projects MAT2011–25046 and MAT2014–57915-R, co-financed by FEDER), Dutch organization for Fundamental Research on Matter (FOM), NWO/OCW and the Comunidad Autonoma de Madrid (MAD2D-CM -S2013/MIT-3007- and NANOFRONTMAG-CM -S2013/MIT-2850) and the Generalitat Valenciana (Prometeo Program) are gratefully acknowledged. AC-G acknowledges financial support from the BBVA Foundation through the fellowship ‘I Convocatoria de Ayudas Fundacion BBVA a Investigadores, Innovadores y Creadores Culturales’ (‘Semiconductores ultradelgados: hacia la optoelectronica flexible’), from the MINECO (Ramón y Cajal 2014 program, RYC-2014-01406) and from the MICINN (MAT2014-58399-JIN). We are grateful to the Electronic Microscopy team at Central Support Service in Experimental Research (SCSIE, University of Valencia, Spain) for their kind and constant support.
Author information
Authors and Affiliations
Contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript. E.N.-M. jointly conceived the study with J.O.I., designed and performed the measurements and prepared the manuscript; S.M.-V. and E.P.-C. helped with the preparation and characterization of samples and contributed to the edition of the manuscript. L.C. created the theoretical model with contributions from J.A.S.-G. and F.G. supervised the theoretical analysis and edited the manuscript. J.Q. and G.R.-B. carried out optical microcopy measurements model and interpret. A.C.-G., N. A., G.A.S., H.S.J. van der Z. and E.C. supervised the study and edited the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-14, Supplementary Notes 1-6 and Supplementary References (PDF 1103 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Navarro-Moratalla, E., Island, J., Mañas-Valero, S. et al. Enhanced superconductivity in atomically thin TaS2. Nat Commun 7, 11043 (2016). https://doi.org/10.1038/ncomms11043
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms11043
This article is cited by
-
Endotaxial stabilization of 2D charge density waves with long-range order
Nature Communications (2024)
-
Thickness dependence of superconductivity in layered GeP5
Rare Metals (2024)
-
Atomically Substitutional Engineering of Transition Metal Dichalcogenide Layers for Enhancing Tailored Properties and Superior Applications
Nano-Micro Letters (2024)
-
Two-dimensional heavy fermions in the van der Waals metal CeSiI
Nature (2024)
-
Anomalous enhancement of charge density wave in kagome superconductor CsV3Sb5 approaching the 2D limit
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.