Abstract
The magnetic field-induced changes in the conductivity of metals are the subject of intense interest, both for revealing new phenomena and as a valuable tool for determining their Fermi surface. Here we report a hitherto unobserved magnetoresistive effect in ultra-clean layered metals, namely a negative longitudinal magnetoresistance that is capable of overcoming their very pronounced orbital one. This effect is correlated with the interlayer coupling disappearing for fields applied along the so-called Yamaji angles where the interlayer coupling vanishes. Therefore, it is intrinsically associated with the Fermi points in the field-induced quasi-one-dimensional electronic dispersion, implying that it results from the axial anomaly among these Fermi points. In its original formulation, the anomaly is predicted to violate separate number conservation laws for left- and right-handed chiral (for example, Weyl) fermions. Its observation in PdCoO2, PtCoO2 and Sr2RuO4 suggests that the anomaly affects the transport of clean conductors, in particular near the quantum limit.
Similar content being viewed by others
Introduction
The magnetoconductivity or -resistivity of metals under a uniform magnetic field μ0H (μ0 is the permeability of free space) is highly dependent on the precise shape of their Fermi surface (FS) and on the orientation of the current flow relative to the external applied field H1,2. This is particularly true for high-purity metals at low temperatures, whose carriers may execute many cyclotronic orbits in between scattering events. However, the description of the magnetoconductivity of real systems in terms of the Boltzmann equation including the Lorentz force, the electronic dispersion and realistic scattering potentials is an incredibly daunting task, whose approximate solutions can only be obtained through over simplifications. Despite the inherent difficulty in describing the magnetoresistivity of metallic or semi-metallic systems, it continues to be a subject of intense interest. Indeed, in recent years, a number of new magnetoresistance phenomena have been uncovered. For example, although semi-classical transport theory predicts a magnetoresistivity ρ(μ0H)∝(μ0H)2, certain compounds such as β-Ag2Te display a linear, non-saturating magnetoresistivity3, which is ascribed to the quantum magnetoresistive scenario4, associated with linearly dispersing Dirac-like bands5. However, in semi-metals characterized by a bulk Dirac dispersion and extremely high electron mobilities such as Cd3As2, the linear magnetoresistivity develops a weak (μ0H)2 term as the quality of the sample increases6. Its enormous magnetoresistivity is claimed to result from the suppression of a certain protection against backscattering channels6. The semi-metal WTe2 was also found to display a very large and non-saturating magnetoresistivity, which is ∝(μ0H)2 under fields up to 60 T. This behaviour was ascribed to a nearly perfect compensation between the densities of electrons and holes7. In recent times, a series of compounds were proposed to be candidate Weyl semi-metals characterized by a linear touching between the valence and the conduction bands at several points (Weyl points) of their Brillouin zone8. These Weyl points are predicted to lead to a pronounced negative magnetoresistivity for electric fields aligned along a magnetic field due to the so-called axial anomaly9,10.
Here we unveil the observation of yet another magnetoresistive effect, namely a pronounced negative magnetoresistivity in extremely clean and non-magnetic layered metals. We study the delafossite-type PtCoO2 and PdCoO2 compounds, which are characterized by a single FS sheet and, as with Cd3As2, can display residual resistivities on the order of a just few tenths of nΩ cm. Given its extremely low level of disorder, for specific field orientations along which the interlayer coupling vanishes, PdCoO2 can display a very pronounced positive magnetoresistivity that exceeds 550,000% for μ0H≃35 T and for currents along the interlayer axis. Nevertheless, as soon as the field is rotated away from these specific orientations and as the field increases, this large orbital effect is overwhelmed by the emergence of a pronounced negative magnetoresistivity. For fields along the interlayer direction, a strong longitudinal negative magnetoresistivity is observed from μ0H=0 T to fields all the way up to μ0H=35 T. Very similar behaviour is observed in the PtCoO2 compound. For the correlated Sr2RuO4, the longitudinal negative magnetoresistivity effect is also observable but only in the cleanest samples, that is, those displaying the highest superconducting transition temperatures. We suggest that this effect might result from the axial anomaly between Fermi points in a field-induced, quasi-one-dimensional electronic dispersion.
Results
Observation of an anomalous longitudinal magnetoresistivity
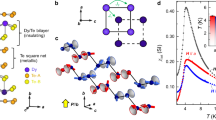
As shown in Fig. 1a, PdCoO2 crystallizes in the space group  , which results from the stacking of monatomic triangular layers11. The synthesis of PdCoO2 single crystals is described in the Methods section. According to band structure calculations12,13,14, the Fermi level EF is placed between the filled t2g and the empty eg levels with the Pd triangular planes dominating the conductivity and leading to its highly anisotropic transport properties. The reported room temperature in-plane resistivity is just 2.6 μΩ cm, making PdCoO2 perhaps the most conductive oxide known to date15. Figure 1b,c show the configuration of contacts used for measuring the longitudinal magnetoresistivity of all compounds. de Haas van Alphen measurements15 reveal a single, corrugated and nearly two-dimensional FS with a rounded hexagonal cross-section, in broad agreement with both band structure calculations12,13,14 and angle-resolved photoemission measurements16. de Haas van Alphen yields an average Fermi wave vector
, which results from the stacking of monatomic triangular layers11. The synthesis of PdCoO2 single crystals is described in the Methods section. According to band structure calculations12,13,14, the Fermi level EF is placed between the filled t2g and the empty eg levels with the Pd triangular planes dominating the conductivity and leading to its highly anisotropic transport properties. The reported room temperature in-plane resistivity is just 2.6 μΩ cm, making PdCoO2 perhaps the most conductive oxide known to date15. Figure 1b,c show the configuration of contacts used for measuring the longitudinal magnetoresistivity of all compounds. de Haas van Alphen measurements15 reveal a single, corrugated and nearly two-dimensional FS with a rounded hexagonal cross-section, in broad agreement with both band structure calculations12,13,14 and angle-resolved photoemission measurements16. de Haas van Alphen yields an average Fermi wave vector  m−1or an average Fermi velocity
m−1or an average Fermi velocity  m s−1 (where μ≃1.5 is the carrier effective mass15 in units of free electron mass). Recent measurements of interplanar magnetoresistivity ρc(μ0H) reveal an enormous enhancement for fields along the
m s−1 (where μ≃1.5 is the carrier effective mass15 in units of free electron mass). Recent measurements of interplanar magnetoresistivity ρc(μ0H) reveal an enormous enhancement for fields along the  direction, that is, increasing by ∼35,000% at 2 K under μ0H=14 T, which does not follow the characteristic ρ(μ0H)∝(μ0H)2 dependence at higher fields17. This behaviour can be reproduced qualitatively by semi-classical calculations, assuming a very small scattering rate17. Most single crystals display in-plane residual resistivities ρab0 ranging from only ∼10 up to ∼40 nΩ cm, which correspond to transport lifetimes
direction, that is, increasing by ∼35,000% at 2 K under μ0H=14 T, which does not follow the characteristic ρ(μ0H)∝(μ0H)2 dependence at higher fields17. This behaviour can be reproduced qualitatively by semi-classical calculations, assuming a very small scattering rate17. Most single crystals display in-plane residual resistivities ρab0 ranging from only ∼10 up to ∼40 nΩ cm, which correspond to transport lifetimes  ranging from 20 down to ≃5.5 ps (e is the electron charge and n≃2.4 × 1028 m−3 (ref. 11)) or mean free paths
ranging from 20 down to ≃5.5 ps (e is the electron charge and n≃2.4 × 1028 m−3 (ref. 11)) or mean free paths  ranging from ∼4 up to 20 μm (ref. 15). However, according to ref. 15, the quasiparticle lifetime
ranging from ∼4 up to 20 μm (ref. 15). However, according to ref. 15, the quasiparticle lifetime  extracted from the Dingle temperature becomes (in units of length)
extracted from the Dingle temperature becomes (in units of length)  μm. Hence, the transport lifetime is larger than the quasiparticle lifetime by at least one order of magnitude, which is the hallmark of a predominant forward scattering mechanism (see ref. 18). For a magnetic field along c axis,
μm. Hence, the transport lifetime is larger than the quasiparticle lifetime by at least one order of magnitude, which is the hallmark of a predominant forward scattering mechanism (see ref. 18). For a magnetic field along c axis,  when μ0H1 T; in contrast,
when μ0H1 T; in contrast,  when μ0H>10 T. These estimations suggest the importance of the Landau quantization for understanding our observations over a wide range of fields up to μ0H∼30 T.
when μ0H>10 T. These estimations suggest the importance of the Landau quantization for understanding our observations over a wide range of fields up to μ0H∼30 T.
(a) Crystallographic structure of the delafossite PdCoO2 with Pd, Co and O atoms shown in green, blue and red, respectively. (b) Configuration of contacts for measuring the interplanar longitudinal resistivity (ρc), showing concentric contacts at the top and at the bottom surface of each hexagonal platelet-like crystal. (c) Configuration of contacts for measuring the in-plane longitudinal resistivity  for currents flowing along the
for currents flowing along the  axis and fields applied along the same direction.
axis and fields applied along the same direction.
As shown in Fig. 2a, the low-T magnetoresistivity or Δρc=(ρc−ρ0)/ρ0, where ρ0 is the zero-field interplanar resistivity, decreases (up to ∼70%) in a magnetic field of 30 T oriented parallel to the applied current. Given that PdCoO2 is non-magnetic and extremely clean (see Methods), this effect cannot be attributed to magnetic impurities. In addition, the magnitude of the observed magnetoresistivity cannot be explained in terms of weak localization effects19,20. To support both statements, in Fig. 2b we show Δρc for a PdCoO2 single crystal as a function of H applied along the  planar direction and for several temperatures T. In sharp contrast to results shown in Fig. 2a, as T decreases, Δρc(μ0H) increases considerably, by more than three orders of magnitude when T<10 K, thus confirming the absence of scattering by magnetic impurities or any role for weak localization. In addition, it is noteworthy that Δρc∝(μ0H)2 at low fields, which indicates that the interlayer transport is coherent at low fields21. Figure 2c depicts a simple Kohler plot of the magnetoresistivity shown in Fig. 2b, where the field has also been normalized by ρ0(T), which indicates unambiguously that the transverse magnetoresistive effect in PdCoO2 is exclusively orbital in character and is dominated by the scattering from impurities/imperfections and phonons1.
planar direction and for several temperatures T. In sharp contrast to results shown in Fig. 2a, as T decreases, Δρc(μ0H) increases considerably, by more than three orders of magnitude when T<10 K, thus confirming the absence of scattering by magnetic impurities or any role for weak localization. In addition, it is noteworthy that Δρc∝(μ0H)2 at low fields, which indicates that the interlayer transport is coherent at low fields21. Figure 2c depicts a simple Kohler plot of the magnetoresistivity shown in Fig. 2b, where the field has also been normalized by ρ0(T), which indicates unambiguously that the transverse magnetoresistive effect in PdCoO2 is exclusively orbital in character and is dominated by the scattering from impurities/imperfections and phonons1.
(a) Normalized interplanar magnetoresistivity Δρc/ρ0=(ρc(μ0H)−ρ0)/ρ0, where ρ0 is the resistivity at zero field, for a PdCoO2 single crystal and as a function of  axis at T=1.4 K. The very pronounced negative longitudinal magnetoresistance arising in the presence of cyclotron motion in the ab plane is noteworthy. (b) Δρc(μ0H)/ρ0 as a function of μ0H applied along the
axis at T=1.4 K. The very pronounced negative longitudinal magnetoresistance arising in the presence of cyclotron motion in the ab plane is noteworthy. (b) Δρc(μ0H)/ρ0 as a function of μ0H applied along the  direction and for several temperatures T, describing positive transverse magnetoresistance. At T=1.4 K, Δρc surpasses 350,000% under a field H=35 T. (c) Kohler scaling of the transverse positive magnetoresistance Δρc(μ0H). It is noteworthy that (i) all data collapse on a single curve as a function of μ0H/ρ0 and (ii) at low fields Δρc(μ0H)/ρ0∝(μ0H/ρ0)2 as expected for classical orbital magnetoresistance.
direction and for several temperatures T, describing positive transverse magnetoresistance. At T=1.4 K, Δρc surpasses 350,000% under a field H=35 T. (c) Kohler scaling of the transverse positive magnetoresistance Δρc(μ0H). It is noteworthy that (i) all data collapse on a single curve as a function of μ0H/ρ0 and (ii) at low fields Δρc(μ0H)/ρ0∝(μ0H/ρ0)2 as expected for classical orbital magnetoresistance.
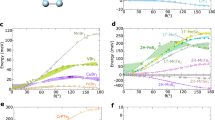
The evolution of the longitudinal magnetoresistance with temperature is depicted in Fig. 3a. ρc is seen to decrease by a factor surpassing 60% for fields approaching 9 T and for all temperatures below 30 K. Figure 3b displays ρc(μ0H)/ρ0 as a function of the angle θ between μ0H and the c axis at a temperature T=1.8 K, for a third single crystal. For θ>10°, the pronounced positive magnetoresistance observed at low fields, due to an orbital magnetoresistive effect, is overpowered at higher fields by the mechanism responsible for the negative magnetoresistivity. This behaviour is no longer observed within this field range when θ is increased beyond ∼20°. Figure 3c shows a Kohler plot, that is, Δρc/ρ0 as a function of μ0H normalized by ρ0. As seen in Fig. 3c, all curves collapse on a single curve, indicating that a particular transport mechanism dominates even at high temperatures where phonon scattering is expected to be strong. The red line is a fit to (μ0H)−1, indicating that  at lower fields.
at lower fields.
(a) Interlayer resistivity ρc normalized by its zero-field value ρ0 as a function of the external field μ0H and for μ0H parallel to current I (itself parallel to the sample interlayer c-axis) and for several temperatures T. It is noteworthy that the very pronounced negative magnetoresistivity, that is, ρc/ρ0 decreases by a factor >60% when sweeping the field from 0 to 5 T. It is also worth noting that this effect disappears when the T approaches and/or surpasses ∼200 K. (b) ρc as a function of μ0H from a third crystal at T=1.8 K and for several angles θ between μ0H and the c axis. It is noteworthy how the negative magnetoresistivity observed at low fields is progressively suppressed as θ increases, becoming strongly positive. Nevertheless, the mechanism leading to the negative magnetoresistivity is observed to overpower the orbital one at higher fields and higher angles. (c) Kohler plot for all the temperature-dependent ρc/ρ0. Red line is a fit of Δρc/ρ0 to (μ0H)−1.
Angular dependence of the anomalous magnetoresistive response
Fig. 4 shows the longitudinal magnetoresistance  for fields and currents along the
for fields and currents along the  axis. For this orientation, the charge carriers follow open orbits along the axis of the cylindrical FS instead of quantized cyclotronic orbits. In contrast to Δρc/ρ0, but similar to the longitudinal magnetoresistivity of ultra-clean elemental metals1,2,
axis. For this orientation, the charge carriers follow open orbits along the axis of the cylindrical FS instead of quantized cyclotronic orbits. In contrast to Δρc/ρ0, but similar to the longitudinal magnetoresistivity of ultra-clean elemental metals1,2,  is observed to increase and saturate as a function of μ0H. This further confirms that conventional mechanisms, for example, impurities, magnetism and so on, are not responsible for the negative longitudinal magnetoresistivity observed in Δρc/ρ0.
is observed to increase and saturate as a function of μ0H. This further confirms that conventional mechanisms, for example, impurities, magnetism and so on, are not responsible for the negative longitudinal magnetoresistivity observed in Δρc/ρ0.
Figure 5a shows ρc as a function of the angle θ between the field and the c axis, for three different field values: 8, 25 and 30 T. ρc(θ) displays the characteristic structure displayed by quasi-two-dimensional metals, namely a series of sharp peaks at specific angles  called the Yamaji angles (where n is an integer, c is the interplanar distance and
called the Yamaji angles (where n is an integer, c is the interplanar distance and  is the projection of the Fermi wave number on the conduction plane), for which all cyclotronic orbits on the FS have an identical orbital area22. In other words, the corrugation of the FS no longer leads to a distribution of cross-sectional areas, as if the corrugation has been effectively suppressed. As discussed below, in terms of the energy spectrum, this means that the Landau levels become non-dispersive at the Yamaji angles18,23; hence, one no longer has Fermi points. The sharp peak at θ=90° is attributed to coherent electron transport along small closed orbits on the sides of a corrugated cylindrical FS24,25. The width of this peak Δθ, shown in Fig. 5b for several temperatures, allows us to estimate the interlayer transfer integral tc (ref. 26),
is the projection of the Fermi wave number on the conduction plane), for which all cyclotronic orbits on the FS have an identical orbital area22. In other words, the corrugation of the FS no longer leads to a distribution of cross-sectional areas, as if the corrugation has been effectively suppressed. As discussed below, in terms of the energy spectrum, this means that the Landau levels become non-dispersive at the Yamaji angles18,23; hence, one no longer has Fermi points. The sharp peak at θ=90° is attributed to coherent electron transport along small closed orbits on the sides of a corrugated cylindrical FS24,25. The width of this peak Δθ, shown in Fig. 5b for several temperatures, allows us to estimate the interlayer transfer integral tc (ref. 26),
(a) Interplanar magnetoresistivity ρc for a PdCoO2 single crystal as a function of the angle θ between the [001] interplanar direction and the external field μ0H. The pronounced peaks observed as a function of θ are the so-called Yamaji-effect peaks22. (b) Interlayer coherence peak observed for fields nearly along the interplanar direction, which indicates an extended FS along the interlayer direction24. From the width Δθ of the peak at half maximum, one can estimate the value of the interlayer transfer integral tc=2.79 meV from equation (1). (c) Interplanar resistivity ρc as a function of μ0H at T=1.8 K and for two angles, that is, the Yamaji value θn=1=23.0° and θ=22.7°. It is noteworthy how the pronounced positive magnetoresistivity observed at θn=1 is strongly suppressed when μ0H is rotated by just ∼0.3°, leading to magnetoresistance saturation. (d) ρc as a function of μ0H under T=1.8 K and for θ=21.5°. It is noteworthy how ρc, after increasing by several orders of magnitude, displays negative magnetoresistivity at higher fields, thus indicating a clear competition between the orbital and another mechanism, which suppresses the magnetoresistivity. Dotted red line corresponds to a fit of  .
.

assuming a simple sinusoidal FS corrugation along the kz direction. Here, the interplanar separation is d=c/3, as there are three conducting Pd planes per unit cell, each providing one conducting hole and therefore leading to three carriers per unit cell. This value is consistent with our Hall-effect measurements (not included here). The full width at half maximum of the peak at 90° is Δθ≃0.78° and EF is given by  eV; therefore, one obtains tc=2.79 meV or ≃32.4 K. Figure 5c displays ρc as a function of μ0H for two angles; the Yamaji angle θn=1=23.0° and θ=22.7°, respectively. As seen, ρc(μ0H) for fields along θn=1 displays a very pronounced positive magnetoresistance, that is, ρc/ρ0 increases by ∼550,000% when μ0H is swept from 0 to 35 T. However, at μ0H=35 T, ρc/ρ0 decreases by one order of magnitude as μ0H is rotated by just ∼0.3° with respect to θn=1. Furthermore, as seen in Fig. 5d, at higher fields ρc displays a cross-over from a very pronounced and positive to a negative magnetoresistance, resulting from a small increment in θ relative to θn=1. This is a very clear indication for two competing mechanisms, with negative magnetoresistivity overcoming the orbital effect when the orbitally averaged interlayer group velocity (or the transfer integral tc) becomes finite at θ≠θn. We emphasize that for a conventional and very clean metal, composed of a single FS sheet, the magnetoresistivity should either be ∝(μ0H)2 (ref. 21) or saturate as seen in quasi-two-dimensional metals close to the Yamaji angle27, or in Fig. 2a,b for fields below ∼15 T. This is illustrated by the Supplementary Fig. 1 (see also Supplementary Note 1), which contrasts our experimental observations with predictions based on semi-classical transport models, which correctly describe the magnetoresistance of layered organic metals in the vicinity of the Yamaji angle. In contrast, as illustrated by the dotted red line in Fig. 5d, ρc(μ0H) can be well described by the expression
eV; therefore, one obtains tc=2.79 meV or ≃32.4 K. Figure 5c displays ρc as a function of μ0H for two angles; the Yamaji angle θn=1=23.0° and θ=22.7°, respectively. As seen, ρc(μ0H) for fields along θn=1 displays a very pronounced positive magnetoresistance, that is, ρc/ρ0 increases by ∼550,000% when μ0H is swept from 0 to 35 T. However, at μ0H=35 T, ρc/ρ0 decreases by one order of magnitude as μ0H is rotated by just ∼0.3° with respect to θn=1. Furthermore, as seen in Fig. 5d, at higher fields ρc displays a cross-over from a very pronounced and positive to a negative magnetoresistance, resulting from a small increment in θ relative to θn=1. This is a very clear indication for two competing mechanisms, with negative magnetoresistivity overcoming the orbital effect when the orbitally averaged interlayer group velocity (or the transfer integral tc) becomes finite at θ≠θn. We emphasize that for a conventional and very clean metal, composed of a single FS sheet, the magnetoresistivity should either be ∝(μ0H)2 (ref. 21) or saturate as seen in quasi-two-dimensional metals close to the Yamaji angle27, or in Fig. 2a,b for fields below ∼15 T. This is illustrated by the Supplementary Fig. 1 (see also Supplementary Note 1), which contrasts our experimental observations with predictions based on semi-classical transport models, which correctly describe the magnetoresistance of layered organic metals in the vicinity of the Yamaji angle. In contrast, as illustrated by the dotted red line in Fig. 5d, ρc(μ0H) can be well described by the expression  . Here, the ρc∝(μ0H)−1 term describes the negative magnetoresistivity as previously seen in Fig. 3, whereas the ρc∝μ0H term describes the non-saturating linear magnetoresistance predicted and observed for systems close to the quantum limit3,4,5,28. This expression describes ρc(μ0H, θ) satisfactorily, except at the Yamaji angle where both terms vanish. In the neighbourhood of θn, the addition of a small ρc∝(μ0H)2 term improves the fit, with its pre-factor increasing as θn is approached. ρc also displays Shubnikov de Haas oscillations at small (and strongly θ dependent) frequencies, which were not previously detected in ref. 15. As discussed in ref. 29, these slow oscillations, observed only in the interlayer magnetoresistance of layered metals, originate from the warping of the FS. In Supplementary Fig. 2 (See also Supplementary Note 2), we show how these frequencies disappear when the group velocity vanishes at θn.
. Here, the ρc∝(μ0H)−1 term describes the negative magnetoresistivity as previously seen in Fig. 3, whereas the ρc∝μ0H term describes the non-saturating linear magnetoresistance predicted and observed for systems close to the quantum limit3,4,5,28. This expression describes ρc(μ0H, θ) satisfactorily, except at the Yamaji angle where both terms vanish. In the neighbourhood of θn, the addition of a small ρc∝(μ0H)2 term improves the fit, with its pre-factor increasing as θn is approached. ρc also displays Shubnikov de Haas oscillations at small (and strongly θ dependent) frequencies, which were not previously detected in ref. 15. As discussed in ref. 29, these slow oscillations, observed only in the interlayer magnetoresistance of layered metals, originate from the warping of the FS. In Supplementary Fig. 2 (See also Supplementary Note 2), we show how these frequencies disappear when the group velocity vanishes at θn.
Significantly, this effect does not appear to be confined to PdCoO2. Figure 6 presents an overall evaluation of the longitudinal magnetoresistance of isostructural PtCoO2, whereas Supplementary Fig. 3 displays the observation of impurity-dependent negative magnetoresistivity in the correlated perovskite Sr2RuO4 (See also Supplementary Note 3). As shown in Fig. 6, PtCoO2 presents a pronounced negative longitudinal magnetoresistivity either for  c axis or for μ0H close to an Yamaji angle (j is the current density). It also presents a very pronounced and non-saturating magnetoresistivy for fields applied along the Yamaji angle. For both systems, the magnetoresistivity does not follow a single power law as a function of μ0H. In fact, as shown in Supplementary Fig. 4, at θn the magnetoresistivity of the (Pt,Pd)CoO2 system follows a (μ0H)2 dependence for μ0H≲15 T. At intermediate fields, ρ(μ0H) deviates from the quadratic dependence, recovering it again at subsequently higher fields. As Kohler’s rule implies that Δρ/ρ0∝(μ0H/ρ0)2, we argue that the observed increase in slope would imply a field-dependent reduction in scattering by impurities (see Supplementary Fig. 4 and Supplementary Note 4). The precise origin of this suppression in scattering remains to be identified. Nevertheless, the enormous and positive magnetoresistivity observed for fields along θn seems consistent with a simple scenario, that is, an extremely clean system(s) whose impurity scattering weakens with increasing magnetic field. In Sr2RuO4, the negative longitudinal magnetoresistivity is observed only in the cleanest samples and for angles within 10° away from the c axis. This compound is characterized by three corrugated cylindrical FS sheets, each leading to a distinct set of Yamaji angles, making it impossible to completely suppress the interplanar coupling at specific Yamaji angle(s).
c axis or for μ0H close to an Yamaji angle (j is the current density). It also presents a very pronounced and non-saturating magnetoresistivy for fields applied along the Yamaji angle. For both systems, the magnetoresistivity does not follow a single power law as a function of μ0H. In fact, as shown in Supplementary Fig. 4, at θn the magnetoresistivity of the (Pt,Pd)CoO2 system follows a (μ0H)2 dependence for μ0H≲15 T. At intermediate fields, ρ(μ0H) deviates from the quadratic dependence, recovering it again at subsequently higher fields. As Kohler’s rule implies that Δρ/ρ0∝(μ0H/ρ0)2, we argue that the observed increase in slope would imply a field-dependent reduction in scattering by impurities (see Supplementary Fig. 4 and Supplementary Note 4). The precise origin of this suppression in scattering remains to be identified. Nevertheless, the enormous and positive magnetoresistivity observed for fields along θn seems consistent with a simple scenario, that is, an extremely clean system(s) whose impurity scattering weakens with increasing magnetic field. In Sr2RuO4, the negative longitudinal magnetoresistivity is observed only in the cleanest samples and for angles within 10° away from the c axis. This compound is characterized by three corrugated cylindrical FS sheets, each leading to a distinct set of Yamaji angles, making it impossible to completely suppress the interplanar coupling at specific Yamaji angle(s).
Interplanar resistivity ρc normalized by its zero-field value ρ0 for a PtCoO2 single crystal at a temperature T=0.35 K and as a function of the magnetic field μ0H applied along two angles with respect to the c axis, respectively θ=0° (pink line) and 17° (blue line). Dashed magenta line describes the smoothly varying background. Inset: ρc/ρ0 as a function of μ0H applied along the first Yamaji angle θn=22.8°.
Discussion
Negative magnetoresistivity is a common feature of ferromagnetic metals near their Curie temperature, or of samples having dimensions comparable to their electronic mean free path where the winding of the electronic orbits under a magnetic field reduces the scattering from the surface. It can also result from the field-induced suppression of weak localization or from the field-induced suppression of spin-scattering/quantum-fluctuations as seen in f-electron compounds30. None of the compounds described in this study are near a magnetic instability, nor do they contain significant amounts of magnetic impurities or disorder to make them prone to weak localization. The magnitude of this anomalous magnetoresistivity, coupled to its peculiar angular dependence, are in fact enough evidence against any of these conventional mechanisms. Below, we discuss an alternative scenario based on the axial anomaly, which in our opinion explains most of our observations.
The axial anomaly is a fundamental concept of relativistic quantum field theory, which describes the violation of separate number conservation laws of left- and right-handed massless chiral fermions in odd spatial dimensions due to quantum mechanical effects31,32. When three-dimensional massless Dirac or Weyl fermions are placed under parallel electric and magnetic fields, the number difference between the left and the right-handed fermions is expected to vary with time according to the Adler–Bell–Jackiw formula9,33

Here, nR/L are the number operators for the right- and the left-handed Weyl fermions, with the electric and the magnetic field strengths respectively given by E and B. The Dirac fermion describes the linear touching of twofold Kramers degenerate conduction and valence bands at isolated momentum points in the Brillouin zone. By contrast, the Weyl fermions arise due to the linear touching between nondegenerate conduction and valence bands. The axial anomaly was initially proposed to produce a large, negative longitudinal magnetoresistance, for a class of gapless semiconductors, for which the low-energy band structure is described by massless Weyl fermions10. The reason for the negative magnetoresistance is relatively straightforward. The number imbalance due to axial anomaly can only be equilibrated through backscattering between two Weyl points. This involves a large momentum transfer QW. Quite generally the impurity scattering in a material can be modeled by a momentum dependent impurity potential V(Q), where Q is the momentum transfer between the initial and the final electronic states. If V(Q) is a smoothly decreasing function of |Q| (such as Gaussian or Lorentzian), the backscattering amplitude can be considerably smaller than its forward scattering counterparts (occurring with small Q around each Weyl point). Therefore in the presence of axial anomaly the transport lifetime can be considerably larger than the one in the absence of a magnetic field. Consequently the axial anomaly in the presence of parallel E and B fields can give rise to larger conductivity or smaller resistivity i.e., negative magnetoresistance. Recent theoretical proposals for Weyl semi-metals34,35,36,37 followed by experimental confirmation38,39 have revived the interest in the experimental confirmation of the axial anomaly through efforts in detecting negative longitudinal magnetoresistivity40,41,42,43,44,45,46. There are examples of three-dimensional Dirac semi-metals47,48,49, which may be converted, through Zeeman splitting, into a Weyl semi-metal. Examples include Bi1−xSbx at the band inversion transition point between topologically trivial and nontrivial insulators42, and Cd3As2 (ref. 6).
In analogy with the predictions for the axial anomaly between Weyl points, here we suggest that our observations might be consistent with the emergence of the axial anomaly among the Fermi points of a field-induced, one-dimensional electronic dispersion18. In effect, in the presence of a strong magnetic field, the quantization of cyclotron motion leads to discrete Landau levels with one-dimensional dispersion and a degeneracy factor eB/h, see Fig. 7a–c. Consider the low-energy description of a one-dimensional electron gas, in terms of the right- and left-handed fermions obtained in the vicinity of the two Fermi points. In the presence of an external electric field E, the separate number conservation of these chiral fermions is violated according to
(a) The dispersion of Landau levels for a conventional three-dimensional metal placed in an external magnetic field applied along the z-direction. Owing to the underlying parabolic dispersion, each Landau level disperses quadratically as a function of kz, the momentum component along the applied field. Each partially occupied Landau level intersects the Fermi energy EF at two Fermi points, as indicated by the red dots. In the vicinity of the two Fermi points located at kz=±kF,n for the n-th partially filled Landau level, the quasiparticles disperse linearly with opposite group velocities v±,n=±ħkF,n/μ where μ is the effective mass. The ± signs of the group velocity respectively define the chirality of the right- and the left-moving one-dimensional fermions. (b) In contrast, for quasi-two-dimensional metals the Landau levels possess a periodic dispersion relation as a function of kz, owing to the tight binding term 2tc cos(kzd), with interlayer hopping strength and spacing, respectively, given by tc and d. Within the first Brillouin zone defined as −π/d<kz<π/d, each partially filled Landau level again gives rise to a pair of one-dimensional fermions of opposite chirality around the Fermi points. The situation depicted here corresponds to 4tc<ħωc, or when only one Landau level is partially filled. (c) Landau levels for 4tc>ħωc or when multiple Landau levels are partially occupied and each of them gives rise to a pair of chiral fermions.

where nR/L corresponds to the number operators of the right- and left-handed fermions, respectively31,32. Each partially occupied Landau level leads to a set of Fermi points and the axial anomaly for such a level can be obtained from equation 3, after multiplying by eB/h. Therefore, each level has an axial anomaly determined by equation (2). When only one Landau level is partially filled, we have the remarkable universal result for the axial anomaly described by Adler–Bell–Jackiw formula of equation (2). For a non-relativistic electron gas, this would occur at the quantum limit. In contrast, this situation would naturally occur for Dirac/Weyl semi-metals, when the Fermi level lies at zero energy, that is, the material has a zero carrier density. Figure 7b describes the situation for a quasi-two-dimensional electronic system on approaching the quantum limit, or when the interplanar coupling becomes considerably smaller than the inter Landau level separation (for example, in the vicinity of the Yamaji angle). We emphasize that the observation of a pronounced, linear-in-field magnetoresistive component, as indicated by the fit in Fig. 5d, is a strong experimental evidence for the proximity of PdCoO2 to the quantum limit on approaching the Yamaji angle. Therefore, we conclude that the axial anomaly should be present in every three-dimensional conducting system, on approaching the quantum limit. Explicit calculations indicate that the axial anomaly would only cause negative magnetoresistance for predominant forward scattering produced by ionic impurities18,50. ρ(μ0H)∝(μ0H)−1 as observed here (Figs 3 and 5) would result from Gaussian impurities18. As our experimental results show, PdCoO2 is a metal of extremely high conductivity, thus necessarily dominated by small-angle scattering processes and therefore satisfying the forward scattering criterion. In this metal the Landau levels disperse periodically as shown in Fig. 7b,c, depending on the relative strength of the cyclotron energy ħωc=ħeB/μ with respect to the interlayer transfer integral tc. The condition 4tc>ħωc is satisfied when μ0H roughly exceeds 100 T. For this reason, Fig. 7c, with multiple partially occupied Landau levels, describes PdCoO2 for fields along the c axis or for arbitrary angles away from the Yamaji ones. Nevertheless, one can suppress the Fermi points by aligning the field along an Yamaji angle and this should suppress the associated axial anomaly. As experimentally seen, the suppression of the Fermi points suppresses the negative magnetoresistivity, indicating that the axial anomaly is responsible for it.
In summary, in very clean layered metals we have uncovered a very clear correlation between the existence of Fermi points in a one-dimensional dispersion and the observation of an anomalous negative magnetoresistivity. The suppression of these points leads to the disappearance of this effect. This indicates that the axial anomaly and related negative magnetoresistivity would not be contingent on the existence of an underlying three-dimensional Dirac/Weyl dispersion. Instead, our study in PdCoO2, PtCoO2 and Sr2RuO4, which are clean metals with no Dirac/Weyl dispersion at zero magnetic field, indicates that the axial anomaly and its effects could be a generic feature of metal(s) near the quantum limit. Nevertheless, the detection of negative magnetoresistivity would depend on the underlying scattering mechanisms, that is, observable only in those compounds that are clean enough to be dominated by elastic forward scattering18,50. In a generic metal with a high carrier density, it is currently impossible to reach the quantum limit; for the available field strength, many Landau levels would be populated, thus producing a myriad of Fermi points. In this regard, extremely pure layered metals such as (Pd,Pt)CoO2 are unique, as by just tilting the magnetic field in the vicinity of the Yamaji angle one can achieve the condition of a single, partially filled Landau level as it would happen at the quantum limit. An explicit analytical calculation of transport lifetime in the presence of axial anomaly due to multiple partially filled Landau levels is a technically challenging task. Therefore at present we do not have a simple analytical formula for describing the observed (μ0H)−1 behavior of the negative magnetoresistance along the c axis (for magnetic field strengths much smaller than the one required to reach the quantum limit). Nevertheless, the suppression of this negative magnetoresistivity for fields precisely aligned along the Yamaji angles indicates unambiguously that the electronic structure at the Fermi level is at the basis for its underlying mechanism. The observation of (μ0H)−1 behavior in the magnetoresistance around the Yamaji angle (when only one partially filled Landau level contributes) gives us the valuable insight that the anomaly induced negative magnetoresistance is quite robust irrespective of the number of partially filled Landau levels. However the determination of a precise functional form for the magnetoresistance in the presence of multiple partially filled Landau levels remains as a technical challenge for theorists. The situation is somewhat analogous to that of the Weyl semi-metals, which are characterized by a number of Weyl points in the first Brillouin zone37, and apparently with all Weyl points contributing to its negative longitudinal magnetoresistivity46. Hence, our results suggest that the axial anomaly among pairs of chiral Fermi points may play a role in ultra-clean systems even when they are located far from the quantum limit.
Finally, it is noteworthy that negative longitudinal magnetoresistivity is also seen in kish graphite at high fields, which is characterized by ellipsoidal electron- and hole-like FSs, on approaching the quantum limit and before the onset of a many-body instability towards a field-induced insulating density-wave ground state51. As discussed in ref. 18, the axial anomaly on approaching the quantum limit may also play a role for the negative magnetoresistivities observed in ZrTe5 (ref. 52) and in α−(ET)2I3 (ref. 53), indicating that this concept, which is the basis of our work, is likely to be relevant to a number of physical systems, in particular semi-metals.
Methods
Crystal synthesis
Single crystals of PdCoO2 were grown by the self-flux method through the following reaction PdCl2+2CoO→PdCoO2+CoCl2 with starting powders of PdCl2 (99.999%) and CoO (99.99+%). These powders were ground for for up to 60 min and placed in a quartz tube. The tube was sealed in vacuum and heated up to 930 °C in a horizontal furnace within 2 h and subsequently up to 1,000 °C within 6 h, and then cooled down quickly to 580 °C in 1 or 2 h. The tube is heated up again to 700 °C within 2 h, kept at 700 °C for 40 h and then cooled down to room temperature at 40 °C h−1. Single crystals, with sizes of approximately 2.8 × 1.3 × 0.3 mm3 were extracted by dissolving out CoCl2 with hot ethanol.
Single-crystal characterization
These were characterized by powder X-ray diffraction, energy dispersive X-ray analysis and electron probe microanalysis. The powder X-ray diffraction pattern indicated no impurity phases. In the crystals measured for this study, electron probe microanalysis indicated that the ratio of Pd to Co is 0.98:1, and that the amount of Cl impurities is <200 p.p.m.
Experimental setup
Transport measurements were performed by using conventional four-terminal techniques in conjunction with a Physical Properties Measurement System, a 18-T superconducting solenoid and a 35-T resistive magnet, coupled to cryogenic facilities such as 3He systems and variable temperature inserts.
Additional information
How to cite this article: Kikugawa, N. et al. Interplanar coupling-dependent magnetoresistivity in high-purity layered metals. Nat. Commun. 7:10903 doi: 10.1038/ncomms10903 (2016).
References
Pippard, A. B. Magnetoresistance in Metals: Cambridge Studies in Low Temperature Physics 2 Cambridge Univ. Press (1989).
Pippard, A. B. Longitudinal magnetoresistance. Proc. R. Soc. A A282, 464–484 (1964).
Lee, M., Rosenbaum, T. F., Saboungi, M. L. & Schnyders, H. S. Band-gap tuning and linear magnetoresistance in the silver chalcogenides. Phys. Rev. Lett. 88, 066602 (2002).
Abrikosov, A. A. Quantum linear magnetoresistance. Europhys. Lett. 49, 789793 (2000).
Zhang, W. et al. Topological aspect and quantum magnetoresistance of β-Ag2Te. Phys. Rev. Lett. 106, 156808 (2011).
Liang, T. et al. Ultrahigh mobility and giant magnetoresistance in the Dirac semi-metal Cd3As2 . Nat. Mater. 14, 280–284 (2015).
Ali, M. N. et al. Large, non-saturating magnetoresistance in WTe2 . Nature 514, 205–208 (2014).
Huang, S.-M. et al. Theoretical discovery/prediction: Weyl semimetal states in the TaAs material (TaAs, NbAs, NbP, TaP) class. Nat. Commun. 6, 7373 (2015).
Bell, J. S. & Jackiw, R. A PCAC puzzle: π0→γγ in the σ-model. Nuovo Cimento A 60, 47–61 (1969).
Nielsen, H. B. & Ninomiya, M. The Adler-Bell-Jackiw anomaly and weyl fermions in a crystal. Phys. Lett. B 130B, 389–396 (1983).
Takatsu, H. et al. Roles of high-frequency optical phonons in the physical properties of the conductive delafossite PdCoO2 . J. Phys. Soc. Jpn 76, 104701 (2007).
Eyert, V., Frésard, R. & Maignan, A. On the metallic conductivity of the delafossites PdCoO2 and PtCoO2 . Chem. Mater. 20, 2370–2373 (2008).
Seshadri, R., Felser, C., Thieme, K. & Tremel, W. Metal-metal bonding and metallic behavior in some ABO2 delafossites. Chem. Mater. 10, 2189–2196 (1998).
Kim, K., Choi, H. C. & Min, B. I. Fermi surface and surface electronic structure of delafossite PdCoO2 . Phys. Rev. B 80, 035116 (2009).
Hicks, C. W. et al. Quantum oscillations and high carrier mobility in the delafossite PdCoO2 . Phys. Rev. Lett. 109, 11640 (2012).
Noh, H. J. et al. Anisotropic electric conductivity of delafossite PdCoO2 studied by angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 102, 256404 (2009).
Takatsu, H. et al. Extremely large magnetoresistance in the nonmagnetic metal PdCoO2 . Phys. Rev. Lett. 111, 056601 (2013).
Goswami, P., Pixley, J. & Das Sarma, S. Axial anomaly and longitudinal magnetoresistance of a generic three dimensional metal. Phys. Rev. B 92, 075205 (2015).
Hikami, S., Larkin, A. I. & Nagaoka, Y. Spin-orbit interaction and magnetoresistance in the two-dimensional random system. Prog. Theor. Phys. 63, 707–710 (1980).
Bergmann, G. Weak localization in thin films a time-of-flight experiment with conduction electrons. Phys. Rep. 107, 1–58 (1984).
Moses, P. & Mackenzie, R. H. Comparison of coherent and weakly incoherent transport models for the interlayer magnetoresistance of layered Fermi liquids. Phys. Rev. B 60, 7998 (1999).
Yamaji, K. On the angle dependence of the magnetoresistance in quasi-two-dimensional organic superconductors. J. Phys. Soc. Jpn 58, 1520–1523 (1989).
Kurihara, Y. A microscopic calculation of the angular-dependent oscillatory magnetoresistance in quasi-two-dimensional systems. J. Phys. Soc. Jpn 61, 975–982 (1992).
Singleton, J. et al. Test for interlayer coherence in a quasi-two-dimensional superconductor. Phys. Rev. Lett. 88, 037001 (2002).
Hanasaki, H., Kagoshima, S., Hasegawa, T., Osada, T. & Miura, N. Contribution of small closed orbits to magnetoresistance in quasi-two-dimensional conductors. Phys. Rev. B 57, 1336–1339 (1998).
Uji, S. et al. Fermi surface and angular-dependent magnetoresistance in the organic conductor (BEDT-TTF)2Br(DIA). Phys. Rev. B 68, 064420 (2003).
Yagi, R., Iye, Y., Osada, T. & Kagoshima, S. Semiclassical interpretation of the angular-dependent oscillatory magnetoresistance in quasi-two-dimensional systems. J. Phys. Soc. Jpn 59, 3069–3072 (1990).
Hu, J. & Rosenbaum, T. F. Classical and quantum routes to linear magnetoresistance. Nat. Mater. 7, 697–700 (2008).
Kartsovnik, M. V., Grigoriev, P. D., Biberacher, W., Kushch, N. D. & Wyder, P. Slow oscillations of magnetoresistance in quasi-two-dimensional metals. Phys. Rev. Lett. 89, 126802 (2002).
Zeng, B. et al. CeCu2Ge2: challenging our understanding of quantum criticality. Phys. Rev. B 90, 155101 (2014).
Peskin, M. E. & Schroeder, D. V. An Introduction to Quantum Field Theory Addison-Wesley (1995).
Fujikawa, K. & Suzuki, H. Path Integrals and Quantum Anomalies Clarendon Press (2004).
Adler, S. Axial-vector vertex in spinor electrodynamics. Phys. Rev. 177, 2426–2438 (1969).
Wan, X., Turner, A., Vishwanath, A. & Savrasov, S. Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101 (2011).
Xu, G., Weng, H., Wang, Z., Dai, X. & Fang, Z. Chern semimetal and the quantized anomalous Hall effect in HgCr2Se4 . Phys. Rev. Lett. 107, 186806 (2011).
Burkov, A. A. & Balents, L. Weyl semimetal in a topological insulator multilayer. Phys. Rev. Lett. 107, 127205 (2011).
Weng, H. M. et al. Weyl semimetal phase in noncentrosymmetric transition-metal monophosphides. Phys. Rev. X 5, 011029 (2015).
Lv, B. Q. et al. Observation of Weyl nodes in TaAs. Nat. Phys. 11, 724–727 (2015).
Yang, L. X. et al. Weyl semimetal phase in the non-centrosymmetric compound TaAs. Nat. Phys. 11, 728–732 (2015).
Aji, V. Adler-Bell-Jackiw anomaly in Weyl semi-metals: application to pyrochlore iridates. Phys. Rev. B 85, 241101 (2012).
Son, D. T. & Spivak, B. Z. Chiral anomaly and classical negative magnetoresistance of Weyl metals. Phys. Rev. B 88, 104412 (2013).
Kim, H.-J. et al. Dirac versus Weyl fermions in topological insulators: Adler-Bell-Jackiw anomaly in transport phenomena. Phys. Rev. Lett. 111, 246603 (2013).
Parameswaran, S. A., Grover, T., Abanin, D. A., Pesin, D. A. & Vishwanath, A. Probing the chiral anomaly with nonlocal transport in three-dimensional topological semimetals. Phys. Rev. X 4, 031035 (2014).
Burkov, A. A. Chiral anomaly and diffusive magnetotransport in Weyl metals. Phys. Rev. Lett. 113, 247203 (2014).
Kim, K.-S., Kim, H.-J. & Sasaki, M. Boltzmann equation approach to anomalous transport in a Weyl metal. Phys. Rev. B 89, 195137 (2014).
Huang, X. C. et al. Observation of the chiral-anomaly-induced negative magnetoresistance in 3D Weyl semimetal TaAs. Phys. Rev. X 5, 031023 (2015).
Liu, Z. K. et al. Discovery of a three-dimensional topological Dirac semimetal Na3Bi. Science 343, 864–867 (2014).
Neupane, M. et al. Observation of a three-dimensional topological Dirac semimetal phase in high-mobility Cd3As2 . Nat. Commun. 5, 3786 (2014).
Borisenko, S. et al. Experimental realization of a three-dimensional Dirac semimetal. Phys. Rev. Lett. 113, 027603 (2014).
Argyres, P. N. & Adams, E. N. Longitudinal magnetoresistance in the quantum limit. Phys. Rev. 104, 900–908 (1956).
Fauqué, B. et al. Two phase transitions induced by a magnetic field in graphite. Phys. Rev. Lett. 110, 266601 (2013).
Li, Q. et al. Chiral magnetic effect in ZrTe5. Nat. Phys. (in the press).
Tajima, N., Sugawara, S., Kato, R., Nishio, Y. & Kajita, K. Effects of the zero-mode landau level on inter-layer magnetoresistance in multilayer massless Dirac fermion systems. Phys. Rev. Lett. 102, 176403 (2009).
Acknowledgements
We thank S. Das Sarma, V. Yakovenko, L. Balents, E. Abrahams and J. Pixley for useful discussions. The NHMFL is supported by NSF through NSF-DMR-1157490 and the State of Florida. N.K. acknowledges the support from the overseas researcher dispatch program at NIMS. P.M.C.R. and N.E.H. acknowledge the support of the HFML-RU/FOM, member of the European Magnetic Field Laboratory (EMFL). Y.M. is supported by the MEXT KAKENHI 15H05852. L.B. is supported by DOE-BES through award DE-SC0002613.
Author information
Authors and Affiliations
Contributions
N.K. performed the measurements and analysed the data. A.K., E.S.C., D.G., R.B., J.S.B., S.U., K.S., T.T., P.M.C.R. and N.E.H. contributed to the collection of experimental data at high magnetic fields. L.B. provided scientific guidance and P.G. the theoretical interpretation. H.T., S.Y. and Y.M. synthesized and characterized the single crystals. Y.I. and M.N. performed electron probe microanalysis of the measured single crystals, to confirm their high degree of purity. P.G., N.H. and L.B. wrote the manuscript with the input of all co-authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-4, Supplementary Notes 1-4 and Supplementary References (PDF 582 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Kikugawa, N., Goswami, P., Kiswandhi, A. et al. Interplanar coupling-dependent magnetoresistivity in high-purity layered metals. Nat Commun 7, 10903 (2016). https://doi.org/10.1038/ncomms10903
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms10903
This article is cited by
-
Directional ballistic transport in the two-dimensional metal PdCoO2
Nature Physics (2022)
-
Interlayer quantum transport in Dirac semimetal BaGa2
Nature Communications (2020)
-
Spin-dependent scattering induced negative magnetoresistance in topological insulator Bi2Te3 nanowires
Scientific Reports (2019)
-
Rational strain engineering in delafossite oxides for highly efficient hydrogen evolution catalysis in acidic media
Nature Catalysis (2019)
-
Unconventional magneto-transport in ultrapure PdCoO2 and PtCoO2
npj Quantum Materials (2018)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.






 normalized by its zero field value ρ0 as a function of the field applied along the
normalized by its zero field value ρ0 as a function of the field applied along the  direction, for a PdCoO2 single crystal and for several temperatures. The absence of negative magnetoresistivity is noteworthy.
direction, for a PdCoO2 single crystal and for several temperatures. The absence of negative magnetoresistivity is noteworthy.

