Abstract
A key characteristic of human brain activity is coherent, spatially distributed oscillations forming behaviour-dependent brain networks. However, a fundamental principle underlying these networks remains unknown. Here we report that functional networks of the human brain are predicted by harmonic patterns, ubiquitous throughout nature, steered by the anatomy of the human cerebral cortex, the human connectome. We introduce a new technique extending the Fourier basis to the human connectome. In this new frequency-specific representation of cortical activity, that we call ‘connectome harmonics’, oscillatory networks of the human brain at rest match harmonic wave patterns of certain frequencies. We demonstrate a neural mechanism behind the self-organization of connectome harmonics with a continuous neural field model of excitatory–inhibitory interactions on the connectome. Remarkably, the critical relation between the neural field patterns and the delicate excitation–inhibition balance fits the neurophysiological changes observed during the loss and recovery of consciousness.
Similar content being viewed by others
Introduction
Fundamentals of natural processes are expressed by physical laws, quantitative relationships among measured properties that are always true1. Although the discovery of the mechanisms of neuronal excitation provided a milestone in explaining single neuron behaviour2, a fundamental principle underlying the collective neural dynamics has remained largely elusive3.
A characteristic feature of cortical dynamics in mammals is the emergence of behaviour-dependent oscillatory networks spanning five orders of magnitude in the frequency domain4. Recently, strong temporal correlation within widely distributed cortical regions has also been discovered in spontaneous slow (<0.1 Hz) fluctuations of the blood oxygen level-dependent signal measured with functional magnetic resonance imaging (fMRI). This discovery revealed that spontaneous activity, in the absence of any external stimuli or task condition, also exhibits highly structured correlation patterns throughout the brain. Remarkably, the topography of these correlation patterns, termed the resting state networks (RSNs)5,6, closely resembles the functional networks of the human brain identified by various sensory, motor and cognitive paradigms6,7 and have been found to relate to electroencephalography microstates, global brain states occurring in discrete epochs of about 100 ms (refs 8, 9).
The RSNs are thought to emerge from local cortical dynamics and cortico-cortical interactions constrained by the anatomical structure of the human cortex—the human connectome10,11. Indeed, various computational models have explored the spontaneous emergence of such oscillatory networks from anatomical connectivity, local cortical dynamics and cortico-cortical interactions10,12. However, our understanding of neural activity lacks a unified fundamental principle revealing a direct macroscopic description of the collective cortical dynamics3.
Here, we demonstrate that a ubiquitous mathematical framework, eigendecomposition of the Laplace operator, which lies at the heart of theories of heat, light, sound, electricity, magnetism, gravitation and fluid mechanics13, can predict the collective dynamics of human cortical activity at the macroscopic scale. In various natural phenomena, the eigenfunctions of the Laplacian constitute the basis of self-organizing patterns in a system: standing wave patterns emerging in sound-induced vibrations of a guitar string or a metallic plate (first demonstrated as complex sand patterns by Chladni14), patterns of ion motion emerging from electromagnetic interactions15,16, electron wave function of a free particle given by time-independent Schrödinger equation17,18 and even patterns emerging in complex dynamical systems such as the reaction-diffusion models introduced by Turing19, which can explain various instances of biological pattern formation20, are predicted by the eigenfunctions of the Laplace operator21,22 (Fig. 1a). Furthermore, Laplace eigenfunctions computed on one-dimensional domain with periodic boundary conditions such as a circle, correspond to the well-known Fourier basis23. This relation has been utilized to extend the Fourier transform to more complex geometries23 and to define a ‘shape DNA’24 in shape recognition.
(a) Laplace eigenfunctions revealing the mechanical vibrations of rectangular metal plates (1st row)—first demonstrated by Ernst Chladni as patterns formed by sand on vibrating metal plates—and metal plates shaped as mammalian skin (2nd row) resembling different mammalian coat patterns for different frequency vibrations21,22 (images reprinted from22 with permission) as well as electron orbits of the hydrogen atom computed by time-independent Schrödinger’s wave function (3rd row)—shown with increasing energy from left to right—and patterns emerging in electromagnetic interactions between laser-excited ion crystals (last row) (images adapted from15). (b) Workflow for the construction of macroscale connectome model. The graph representation was formed by connecting each node sampled from the cortical surface with its immediate local neighbours and by further including the long-range connections between the end points of the cortico-cortical and thalamo-cortical fibres. (c) Examples from the 20 lowest frequency connectome harmonics. Left: wave number. Right: spatial patterns of synchronous oscillations estimated by the eigenvectors of the connectome Laplacian.
We investigate the extension of Laplace eigenfunctions to the particular structure of the human connectome, the connectome harmonics, as a new representation for macroscale cortical activity. Remarkably, when described in this new connectome-specific extension of the Fourier basis, the RSNs match the spatial patterns (Laplacian eigenfunctions) corresponding to certain natural frequencies (Laplacian eigenvalues). Our results present evidence that Laplace eigenfunctions can provide a simple yet almost universal description for patterns of synchrony throughout the cortex in the resting state. Further, we demonstrate a plausible biological mechanism behind the emergence of these patterns from the cortico-cortical and thalamo-cortical interactions by modelling the excitatory and inhibitory dynamics with a neural field model.
Results
Connectome harmonics predict resting state networks
To define the extension of the Laplace operator applied to the human connectome, we utilized its discrete counterpart, the graph Laplacian. We first created a graph representation for each of 10 human connectomes by combining the cortical surface extracted from MRI data of 10 subjects with the long-range (white matter) cortico-cortical and thalamo-cortical connections generated from cortical fibre tracts derived from diffusion tensor imaging (DTI) data of the same subjects (Fig. 1b). For each subject, we formed the graph representation  of the modelled connectome, where the nodes
of the modelled connectome, where the nodes  −n being the total number of nodes—uniformly sample the curved anatomy of the cortical surface and the edges
−n being the total number of nodes—uniformly sample the curved anatomy of the cortical surface and the edges  incorporate both local and long-range cortico-cortical and thalamo-cortical connections. By computing the graph Laplacian
incorporate both local and long-range cortico-cortical and thalamo-cortical connections. By computing the graph Laplacian  on the introduced representation
on the introduced representation  , we define the discrete counterpart of the Laplace operator applied to the human connectome, the connectome Laplacian, for each individual and estimate its eigenvalue–eigenvector pairs
, we define the discrete counterpart of the Laplace operator applied to the human connectome, the connectome Laplacian, for each individual and estimate its eigenvalue–eigenvector pairs  ,
,  , connectome harmonics (see Methods). It is worth noting that by harmonics here we refer to spatial harmonics—as opposed to temporal harmonics. We will see later that these spatial harmonics can emerge from neuronally plausible dynamics but, at this stage, we are basing our Laplace eigenfunctions on static structural connectomes. It is also important to note that the introduced graph
, connectome harmonics (see Methods). It is worth noting that by harmonics here we refer to spatial harmonics—as opposed to temporal harmonics. We will see later that these spatial harmonics can emerge from neuronally plausible dynamics but, at this stage, we are basing our Laplace eigenfunctions on static structural connectomes. It is also important to note that the introduced graph  differs from previous graph representations of the human connectome used in population models10 in that it does not incorporate any parcellation of the cortical surface and cortico-cortical and thalamo-cortical connections. Thus, it provides a densely sampled connectome model with the minimum amount of discretization possible in the given resolution of the MRI and DTI data. Notably, when the number of uniformly sampled data points taken from the underlying manifold, such as the cortical surface, increases, the graph Laplacian converges to its continuous counterpart, the Laplace–Beltrami operator—the generalization of the Laplacian to non-euclidean geometries such as the curved anatomy of the human cortex25.
differs from previous graph representations of the human connectome used in population models10 in that it does not incorporate any parcellation of the cortical surface and cortico-cortical and thalamo-cortical connections. Thus, it provides a densely sampled connectome model with the minimum amount of discretization possible in the given resolution of the MRI and DTI data. Notably, when the number of uniformly sampled data points taken from the underlying manifold, such as the cortical surface, increases, the graph Laplacian converges to its continuous counterpart, the Laplace–Beltrami operator—the generalization of the Laplacian to non-euclidean geometries such as the curved anatomy of the human cortex25.
In the literature, Laplace eigenvalue–eigenvector pairs (eigenmodes) have received significant attention initially due to their relation to the excitation spectrum of a given geometry: the eigenvalues relate to the natural frequencies, the allowed frequencies of standing waves emerging on that particular geometry, whereas the eigenvectors yield the associated wave patterns18,23. Recent studies demonstrate also the relevance of Laplace eigenmodes for other physical phenomena including the phase extraction of an electron wave function18, the patterns emerging in electromagnetic interactions of ions15,16 and morphogenesis22,26 (Fig. 1a). Here, we utilized the eigenvectors of the connectome Laplacian to describe the spatio-temporal patterns of macroscale neural activity.
We found that the eigenvectors of the connectome Laplacian, the connectome harmonics, yield frequency-specific spatial patterns across distributed cortical regions (Fig. 1c; Supplementary Fig. 1). Here the red–blue patterns represent examples from the first 20 connectome harmonics in ascending order of frequency (wavenumber—shown in left) for one representative subject.
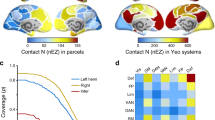
To quantitatively evaluate any similarity between the connectome harmonics and seven RSNs (Fig. 2a), commonly observed in the human brain; default mode, control, dorsal attention, ventral attention, visual, limbic and somato-motor network, we measured the mutual information between the reference RSNs27 and each of the connectome harmonic patterns (Fig. 2b: filled, coloured data points). As a control, we performed Monte Carlo simulations (2,000 simulations per subject randomly combined to 500,000 simulations for group average), in which we randomized the long-range white-matter cortico-cortical and thalamo-cortical connections while preserving the local anatomical structure of the subject’s cortical surface and computed the harmonics of each randomized network using the same methodology (Fig. 2b: black data points). Crucially, we found statistically significant similarity between the default mode network (DMN) and one particular connectome harmonic (in the range of the 9th connectome harmonic, ±2 due to individual differences) in the group average (Fig. 2b, top row, *P<0.0002, **P<0.0001; 500,000 Monte Carlo simulations for group average, corrected for multiple comparisons) as well as for all 10 subjects individually (Supplementary Fig. 2, P-values: *P<0.05, **P<0.02; 2,000 Monte Carlo simulations per subject, corrected for multiple comparisons). For all other resting state networks, we observed larger individual differences in the mutual information values (Supplementary Figs 2 and 3), while the Monte Carlo simulations still yielded significant similarity for different ranges of the connectome harmonics in the group analysis (Fig. 2b). In particular, we found that the visual, somato-motor and limbic networks showed significant similarity to only low-frequency connectome harmonics, while networks associated with higher cognitive functions, that is, control, dorsal attention and ventral attention, significantly matched a broad range of connectome harmonics distributed over the spatial frequency spectrum.
(a) Patterns of synchronous oscillations, i.e., the RSNs, of the human brain overlap with the established functional systems, i.e., groups of cortical regions, which coactivate during certain tasks6,7. For quantitative evaluation of any similarity between the RSNs and connectome harmonics, we use the seven RSNs (default mode, control, dorsal attention, ventral attention, visual, limbic and somato-motor networks) (shown in a) identified from 1,000 subjects’ intrinsic functional connectivity data27. (b) Similarity measured by mutual information and (c) predictive power measured by F-measure values between the connectome harmonics with 40 lowest frequencies and the reference RSNs in ref. 27 (shown in a) compared with those of randomized harmonics (*P<0.0002, **P<0.0001 estimated by Monte Carlo simulations with 2,000 simulations per subject and 500,000 simulations for group average, after multiple comparison correction by false discovery rate, error bars indicate standard error across 10 subjects).
To further assess the predictive power of connectome harmonics for the resting state networks, we utilized an information retrieval metric, F-measure, which simultaneously quantifies the recall and precision of connectome harmonics’ prediction of the RSNs. We computed F-measure values between the connectome harmonics (after applying a binary indicator function) and the binary patterns of the RSNs27 and compared it with the F-measure values of randomized harmonics derived from Monte Carlo simulations. The F-measure provides a stricter evaluation than the information theoretic mutual information, as the indicator function imposes a binary decision to each node. This evaluation (Fig. 2c; Supplementary Figs 4 and 5) confirmed our previous findings based on mutual information. Taken together, these results suggest that the visual, somato-motor, and limbic, as well as the default mode network, are well predicted by individual connectome harmonics of a narrow frequency range, whereas the higher cognitive networks rely on a broader frequency range of connectome harmonics distributed over the spatial spectrum.
Connectome harmonics as the Fourier basis on the connectome
Next, we investigated the use of connectome harmonics as a function basis to represent spatial patterns of cortical networks. The orthogonality of connectome harmonics means that a linear combination of these eigenfunctions can be used to recreate any spatial pattern of neural activity. The importance of the connectome harmonic basis lies in its close ties to the classical Fourier transform, which corresponds to the decomposition of a signal into a linear combination of the eigenfunctions of the Laplace operator applied to a circular domain, that is, sine and cosine functions with different frequencies23. Since connectome harmonics are defined as the eigenvectors of the connectome Laplacian—the discrete counterpart of the Laplacian applied to the human connectome—they extend the Fourier basis to the particular geometry of the human connectome. Hence, the spectral transform onto the connectome harmonic basis naturally extends the classical Fourier transform to the human connectome.
To analyse the spatial frequency content of the resting state networks27 (Fig. 2a), we performed a spectral transform to the connectome harmonic basis and reconstructed the spatial patterns of individual networks. Although the binary nature of the reference networks theoretically necessitates the use of the whole connectome harmonic spectrum for reconstruction—the same way that a square wave can only be reconstructed using the sine waves with infinite many frequencies—sharp decreases in the normalized reconstruction errors were observed by using just 0.1% of the connectome harmonic spectrum (low-frequency range; Fig. 3a). The steepest decrease of the DMN’s reconstruction error occurred for the frequency band that also showed significant similarity and predictive power in mutual information and F-measure values, respectively (highlighted by the red column in Fig. 3a, best matching connectome harmonic of each subject shown in Supplementary Fig. 6, reconstruction shown in Fig. 3c) while for the visual, somato-motor and limbic networks the decrease of the reconstruction error remained large but constant within 0.1% of the spectrum (Fig. 3a). Slower convergence was observed for the reconstruction errors of higher cognitive networks within the range of 1.2% of the spectrum (low-frequency range) suggesting the reliance of these networks on a broader range of frequencies (Fig. 3b). These results confirm our previous findings while providing a novel analytical language of cortical activity analogous to the classical Fourier transform that can be utilized to quantify any activity pattern including task-based event-related designs.
Normalized reconstruction error of each resting state network using (a) 0.1% and (b) 1.2% of the connectome harmonics spectrum averaged across 10 subjects (error bars and shading indicate standard error across 10 subjects) compared to the reconstruction of a randomized binary pattern. Red band in a highlights the steepest decrease for the DMN. (c) Reconstruction of the DMN using (from top to bottom) 5, 0.5 and 0.05% of the spectrum and the best matching connectome harmonic of one subject’s data.
Biological mechanisms underlying connectome harmonics
We also investigated the biological mechanisms likely to underlie the self-organization of connectome harmonics on the cortex. Hitherto, we have assumed that the graph Laplacian based upon structural connectivity provides a plausible proxy for the effective connectivity (also known as the Jacobian-please see ref. 28) of an underlying neuronal dynamical system. In what follows, we explore the biological mechanisms likely to underlie these neuronal dynamics. In particular, we exploit the efficient description of these dynamics given by neural field equations in terms of connectome harmonics and show how they give rise to the emergence of connectome harmonics on the cortex.
The dynamics of the oscillatory cortical networks is thought to emerge from the interplay of excitation; for instance mediated by glutamatergic principal cells, and inhibition; for instance mediated γ-aminobutyric acid GABAergic interneurons29. To describe macroscale cortical dynamics, we extend a variant of neural field models based on Wilson–Cowan equations, the most commonly utilized mathematical description of the excitatory–inhibitory neural dynamics30. Neural field models based on Wilson–Cowan equations are a variant of reaction-diffusion systems31 originally introduced by Turing as a mathematical model for morphogenesis19. Based on the principle that mutual interactions between a diffusing activator and inhibitor can result in self-organizing pattern formation, reaction-diffusion models have provided valuable insights into the mechanisms underlying the emergence of non-linear waves in several biological processes including morphogenesis19,20, formation of ocular dominance patterns in the visual cortex32, visual hallucinations33,34 and interactions of excitatory and inhibitory activity in neural populations of the cortical and thalamic tissue30,35. Crucially, the pattern formation in reaction-diffusion systems is caused by the exponential growth of certain eigenfunctions of the Laplacian applied to the patterning domain (see refs 21, 22 and Supplementary Notes 1–4). The selection of which harmonic patterns are ‘activated’ (grow) is determined by the diffusion parameters of excitation and inhibition (Supplementary Fig. 7). Hence, the Laplace eigenfunctions provide the building blocks of complex patterns emerging in reaction-diffusion systems.
On a two-dimensional continuous idealization of the cortex, the Wilson–Cowan equations lead to self-organization of neural oscillatory patterns when short-range excitation is coupled with broader lateral inhibition36. This type of functional circuitry, known as ‘Mexican hat’ organization37 or centre-on and surround-off connectivity38 is well-observed experimentally in the early visual cortex, known as cortical surround suppression39,40 and is likely to extend throughout the neocortex41,42.
Recent experimental evidence showed that a plausible mechanism underlying the cortical surround suppression in V1 is the activity of the somatostatin-expressing inhibitory neurons in the superficial layers of the mouse visual cortex and a similar neural circuit is also likely to underlie surround suppression in other cortical areas42. These findings are further supported by the report of broader spatial extent of inhibition compared with excitation in the primary visual cortex of awake mice43. Furthermore, layer-specific suppression and facilitation also generates the necessary circuits for lateral inhibitory interactions29,44: coordinated modulation of superficial (L2/3) and deep cortical layers (L5) gives rise to competition between neighbouring domains and lateral inhibition, although the spatial extent of excitation and inhibition across cortical domains show overlapping distributions vertically (across cortical layers) and horizontally (within layers)44. Notably, it has been shown that the Mexican hat type of functional circuitry can also be generated in anatomical circuits with short-range inhibition when a fraction of the total excitatory conductance is slower than the inhibition37. A potential biological source of slower excitatory conduction is the slow synaptic transmission caused by the N-methyl-D-aspartate receptors contributing mostly to excitatory currents37.
Taken together, this converging evidence suggests that various biological mechanisms can give rise to the functional circuitry equivalent to short-range excitation coupled with broad inhibition, which indeed is the necessary condition for the self-organization of oscillatory patterns in Wilson–Cowan-type neural field models30,33,35 (Supplementary Notes 1–5). Next, we extend the Wilson–Cowan equations to the full structural connectivity of the thalamo-cortical system by incorporating the connectome Laplacian and demonstrate the relation between the emerging oscillatory patterns and the connectome harmonics.
Neural field model of connectome-wide neural dynamics
We extended a variant of the neural field model35 based on the Wilson–Cowan equations30 to the three-dimensional connectome model by incorporating the connectome Laplacian into the spatial propagation (diffusion) term (Fig. 4a; Supplementary Notes 2 and 3). Numerical simulations were then performed by combining the network diffusion on the human connectome—modelled by iterative application of symmetric graph Laplacian23,45  —with the excitatory–inhibitory reaction dynamics (Fig. 4a). This allows us to extend continuous form neural field models by incorporating the connectivity of the human connectome. This neural field approach differs from previous macroscale simulations10,46 in that spatial propagation is modelled by network diffusion, as opposed to discrete coupling, yielding a (spatially) near-continuous model of cortical dynamics.
—with the excitatory–inhibitory reaction dynamics (Fig. 4a). This allows us to extend continuous form neural field models by incorporating the connectivity of the human connectome. This neural field approach differs from previous macroscale simulations10,46 in that spatial propagation is modelled by network diffusion, as opposed to discrete coupling, yielding a (spatially) near-continuous model of cortical dynamics.
(a) Left: dynamics of excitatory (E) and inhibitory (I) activity. Right: time evolution of the excitatory E(vi, t) and inhibitory I(vi, t) activity at the cortical location  at time t where
at time t where  ,
,  ,
,  and
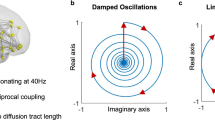
and  describe the diffusion processes of E and I activity acting on excitatory (EE, IE) and inhibitory (EI, II) neural populations and τs refers to the units of system time, that is, characteristic time scale. (b) Linear stability analysis of the neural field model in terms of connectome harmonics. The red regions correspond to the diffusion parameters in the phase space that algebraically satisfy the necessary condition for oscillations, that is, the critical Hopf regime, plotted as a function of the analysed diffusion parameter vertical axis and the eigenvalue of the connectome harmonic horizontal axis. (c) Power spectrum of the temporal oscillations in (a total of 267) numerical simulations averaged over all nodes. (d) Spatial pattern for an arbitrary time slice and the temporal profile of four seed locations shown in e. (f) Seed-based correlation analysis of the neural field patterns demonstrates the decoupling between the posterior and anterior midline nodes of the DMN for the same set of parameters leading to slow cortical oscillations.
describe the diffusion processes of E and I activity acting on excitatory (EE, IE) and inhibitory (EI, II) neural populations and τs refers to the units of system time, that is, characteristic time scale. (b) Linear stability analysis of the neural field model in terms of connectome harmonics. The red regions correspond to the diffusion parameters in the phase space that algebraically satisfy the necessary condition for oscillations, that is, the critical Hopf regime, plotted as a function of the analysed diffusion parameter vertical axis and the eigenvalue of the connectome harmonic horizontal axis. (c) Power spectrum of the temporal oscillations in (a total of 267) numerical simulations averaged over all nodes. (d) Spatial pattern for an arbitrary time slice and the temporal profile of four seed locations shown in e. (f) Seed-based correlation analysis of the neural field patterns demonstrates the decoupling between the posterior and anterior midline nodes of the DMN for the same set of parameters leading to slow cortical oscillations.
We found that structured oscillatory patterns naturally self-organize on the human connectome for a wide-range of diffusion parameters in the model (Fig. 4a–d; Supplementary Figs 8 and 9; Supplementary Movies 1–4). Linear stability analysis of the neural field model revealed that a wide range of connectome harmonics could be activated for different diffusion speeds of excitation and inhibition (Fig. 4b; Supplementary Notes 3–5), rendering the neural field model a plausible neural mechanism for the self-organization of connectome harmonics. In particular, we observed a decrease in the frequency of coherent oscillations when excitatory activity is decreased, modelled by slower diffusion of excitation, or when inhibitory activity is increased, modelled by faster diffusion of inhibition in the neural field model (Fig. 4c,d). This relationship between the frequency of temporal oscillations and the excitation–inhibition balance shows remarkable overlap with the neurophysiological changes observed during the loss and recovery of consciousness (for the analysed parameter range). Neurophysiological evidence suggests that drug- or sleep-induced loss of consciousness is associated with increasing inhibitory or decreasing excitatory activity, which is accompanied by a transition from the low amplitude, high-frequency patterns to low-frequency coherent oscillations in cortical activity47. Recent work also shows gradual decoupling between the posterior and anterior midline nodes of the DMN during loss of consciousness48,49. We observed this decoupling in seed-based correlation analysis of the neural field patterns for the exact parameters, which resulted in slower cortical oscillations (Fig. 4e,f; Supplementary Fig. 9).
Finally, we tested the stability of the emerging oscillatory patterns to external perturbations such as noise using Lyapunov stability analysis50. This method involves perturbing the system at some time t* and observing whether the perturbed system converges to the original system. In dynamical systems, such as described by neural field models, the eigenvalues of the linearized system around a known fixed point immediately reveals the local behaviour of the system; that is, it would allow one to identify the unstable ‘growing’ eigenmodes that dominate observed fluctuations (Supplementary Notes 3–5). However, due to the nonlinearities inherent in the Wilson–Cowan equations as well as the high dimensionality of the modelled system, the continuum of the fixed points, that is, the trajectory, was not readily obtainable analytically. Therefore, we numerically integrated the system to determine the stable solution, in our case a periodic solution, for certain parameters. We first perturbed the system separately 10 times by white noise at time t* and analysed the largest difference between the unperturbed trajectory and each of the perturbed trajectories over time by computing the L-infinity norm L(t) (see Methods). Fig. 5a shows that L(t) is bounded and converges to ɛ≈0, whereas Fig. 5b,c illustrate the convergence of the limit cycle and the temporal oscillations of the perturbed system to that of the unperturbed system for two example vertices v1 and v2. These results demonstrate that for the analysed parameter range the extended Wilson–Cowan equations (Fig. 4a) are robust to external perturbations such as noise.
Stability of the emerging oscillations to external perturbation is tested by perturbing the neural field model for a sample oscillatory parameter set ( ,
,  ,
,  and
and  ). (a) The distance measure L(t) versus the time from perturbation t−t* where t* denotes the time of perturbation by white noise. Before the perturbation L(t) is identical to 0. L(0) shows how far the perturbed system altered from the underlying oscillatory stable state. After perturbation, that is, when t−t*>0, L(t) approaches 0 showing the system is Lyapunov stable. (b) The convergence of the limit cycle; that is, excitatory activity of two non-adjacent nodes plotted over time, of the perturbed (black solid line) to unperturbed (orange dashed line) system. (c) The original (unperturbed) trajectory (dashed line) and the perturbed trajectory (solid line) for two sample vertices (green and blue lines) after perturbation t−t*∈[0, 5] unit time. The perturbed trajectory converges back to the original trajectory (with a small phase shift) demonstrating that the state corresponding to the original trajectory is Lyapunov stable to small perturbations.
). (a) The distance measure L(t) versus the time from perturbation t−t* where t* denotes the time of perturbation by white noise. Before the perturbation L(t) is identical to 0. L(0) shows how far the perturbed system altered from the underlying oscillatory stable state. After perturbation, that is, when t−t*>0, L(t) approaches 0 showing the system is Lyapunov stable. (b) The convergence of the limit cycle; that is, excitatory activity of two non-adjacent nodes plotted over time, of the perturbed (black solid line) to unperturbed (orange dashed line) system. (c) The original (unperturbed) trajectory (dashed line) and the perturbed trajectory (solid line) for two sample vertices (green and blue lines) after perturbation t−t*∈[0, 5] unit time. The perturbed trajectory converges back to the original trajectory (with a small phase shift) demonstrating that the state corresponding to the original trajectory is Lyapunov stable to small perturbations.
Taken together, the extension of the Wilson–Cowan-type neural field models to the particular structural connectivity of the human connectome provides a biologically plausible, robust mechanism likely to underlie the self-organization of connectome harmonics in the thalamo-cortical system.
Discussion
Our results reveal several notable findings: firstly, by extending a universal mathematical framework, eigendecomposition of the Laplacian, to the anatomical structure of the human connectome, we introduce connectome harmonics—a connectome-specific extension of the Fourier basis—as a new representation to describe and analyse any spatio-temporal patterns of cortical activity. Remarkably, decomposition of the RSNs into the connectome harmonics revealed significant overlap between the resting state networks and certain connectome harmonic patterns. This suggests that connectome harmonics provide a simple explanatory principle linking the dynamics of oscillatory cortical networks to the anatomy of the human connectome. This finding is the first experimental evidence demonstrating that the ubiquitous mathematical framework, eigendecomposition of the Laplacian, when applied to the human connectome, can provide a simple yet almost universal principle possibly underlying the functional networks of the brain.
Secondly, due to the orthogonality, and therefore independence, of the connectome harmonics corresponding to different frequencies (wavenumbers), the set of all connectome harmonics provides a function basis (a new coordinate system or representation) to describe and analyse any spatio-temporal pattern of cortical activity, independent of the imaging modality, experimental design and even species. Although in this work we demonstrate the application of this novel technique for the human connectome, it can be extended to any other mammalian brain, given its structural connectivity. Hence, connectome harmonics provide a new frequency-specific language to describe spatio-temporal patterns of neural activity and open the door to a new dimension of tools available to probe brain dynamics across various species and technologies.
The potential importance of having an efficient basis set (connectome harmonics) may be particularly relevant for dynamic causal modelling. Indeed, the eigenfunctions of the graph Laplacian are used to summarize the activity of cortical patches in dynamic causal models of electromagnetic activity51. From the point of view of dynamic causal modelling for resting state fMRI, the eigenmodes of the functional connectivity have been used as prior constraints on effective connectivity. Our work suggests that these could be replaced with the eigenfunctions of the graph Laplacian of the structural connectome. Furthermore, one could adjudicate between the utility of eigenmodes based on structural and functional connectivity using Bayesian model comparison—that would compromise a further validation of our universal basis set.
Thirdly, we have emphasized the universality of eigenfunctions or eigenmodes of the graph Laplacian, connectome harmonics, in describing coupled dynamical systems; such as neural field models. By using the graph Laplacian defined on the human connectome, we demonstrate how well-studied neural field models such as those based on the Wilson–Cowan equations30 can be extended to the full structural connectivity of the thalamo-cortical system and linked to the RSNs of the human brain. However, as the definition of connectome harmonics is independent of the chosen dynamical model, both analytically and numerically, the introduced mathematical framework of connectome harmonic basis can also be applied to extend other more complex network models; (for example refs 10, 12, 52), to the full structural connectivity of the thalamo-cortical system in (spatially) near-continuous domain.
In fact, recent computational models suggest very rich and complex dynamics, characterized by rapid transitions between a few discrete states of correlated activity can emerge in resting state52, which is initiated by the noise-driven exploration of the repertoire of the correlation states10,12. These computational studies are supported by recent empirical evidence showing complex dynamics between different RSNs. Studies combining the high temporal resolution of magnetoencephalography data with band-width-specific correlation analysis suggest that the RSNs assemble and disassemble over time, enabling communication (through periods of coherent oscillations) not only within but also across different networks53,54,55. Furthermore, fMRI studies using sliding time window correlations instead of averaging correlations over the whole time course found that a discrete set of connectivity states, dominant recurrent patterns of correlated neural activity, emerge and dissolve over tens of seconds56,57. Connectome harmonic basis could provide a novel theoretical framework for linking these recent empirical findings and advanced computational models focusing on noise-driven exploration of the connectivity states, as they reveal the patterns of correlation on the thalamo-cortical system, and define the set of independent connectivity states or building blocks through which complex dynamics can be expressed in a non-parametric manner, for instance without tuning the size of the temporal window for correlation analysis58,59. Hence, re-formulating the dynamical models, such as those in ref. 52, in terms of connectome harmonics could reveal how noise-driven transitions occur between different frequencies and results in communication between different RSNs.
An intuitive understanding of the role of connectome harmonics in describing coupled dynamical systems, in the setting of large-scale brain dynamics, rests on associating the graph Laplacian with the effective connectivity among cortical nodes. In other words, if the graph Laplacian corresponds to a matrix of effective connection strengths, then its eigenfunctions become the eigenmodes or principle components of the functional connectivity. Furthermore, the graph Laplacian or effective connectivity becomes the (negative) partial correlation matrix of observed fluctuations in activity28. This is important because it explains why the eigenmodes based on the graph Laplacian provide a plausible space in which to describe the RSNs based on functional connectivity. This correspondence rests upon undirected connectivity (represented by symmetric adjacency) matrices, which means that one can interpret effective connectivity as mediating a ‘diffusion’ of neuronal activity. To complete this picture, note that the diagonal terms of the graph Laplacian ensure the sum of input connections to any node is zero (see Methods). It is important to note, however, that in contrast to the diffusion process in other physical phenomena, the neural activity propagates not only locally but also through the long-range white-matter thalamo-cortical connections, the ‘diffusion’ process occurs on the particular connectivity of the human connectome. Our description of the universal harmonics implied by the graph Laplacian in terms of diffusion rests on the undirected nature of the structural connectome (represented by a symmetric adjacency matrix). However, we know that reciprocal forward and backward connections show strong asymmetries in the human brain, rendering the conceptual link between the (directed) effective connectivity and diffusion not always valid. Having said this, there is no reason why one cannot pursue modelling and simulation using the eigenmodes of directed effective connectivity matrices28.
In summary, in this work we introduce a new connectome-specific representation of cortical activity patterns and dynamics, which extends the Fourier basis to the structural connectivity of the thalamo-cortical system. Remarkably, when expressed in this new analytic language, RSNs of the human brain overlap with the connectome harmonic patterns of certain frequencies. We demonstrate the self-organization of these connectome-specific harmonics patterns from the interplay of neural excitation and inhibition in coupled dynamical systems as described by neural field models. Interestingly, due to the emergence of these harmonic patterns in various natural phenomena, ranging from acoustic vibrations, electromagnetic interactions and electron wave functions to morphogenesis, it is tempting to suppose that human brain activity might also be governed by the same underlying principles as other natural phenomena.
Methods
Data
Data used in the preparation of this work were obtained and made available by the Human Connectome Project (HCP), WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657), which is funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research and by the McDonnell Center for Systems Neuroscience at Washington University. We use MRI and DTI data of 10 unrelated subjects (six female, age 22–35) provided by the HCP, WU-Minn Consortium, available on https://db.humanconnectome.org/data/projects/HCP_500. All MRI and DTI datasets were preprocessed according to minimal preprocessing guidelines of the HCP protocol and no additional preprocessing was performed.
For quantitative evaluation of the resting state networks (RSNs) we use the parcellation of the cerebral cortex into seven networks (default mode, control, dorsal attention, ventral attention, visual, limbic and somato-motor networks) identified from 1,000 subjects’ intrinsic functional connectivity data27, available on http://surfer.nmr.mgh.harvard.edu/fswiki/CorticalParcellation_Yeo2011.
Workflow
From T1-weighted MRI data of each subject (resolution 0.7 mm), we reconstruct the cortical surfaces separating the white and grey matter, referred to as the white matter surface in the rest of the manuscript, as well as grey matter and the cerebrospinal fluid, referred to as the grey matter surface in the rest of the manuscript, separately for each hemisphere using the Freesurfer Software http://freesurfer.net. We register each cortical surface to the 1,000 subject average cortical surface of the cortical parcellation data (in the rest of the manuscript referred to as average subject, represented by 20,484 vertices), in order to allow for the vertex-to-vertex comparison between the connectome harmonics and the 1,000 subject averaged reference of the resting state networks.
From the DTI data of each subject (resolution 1.25 mm), we extract the white matter cortico-cortical and thalamo-cortical fibres by applying a deterministic tractography algorithm60 using the MATLAB implementation of Vista Lab, Stanford University http://white.stanford.edu/newlm/index.php/MrDiffusion. After registering the DTI data and the cortical surface of each subject, we initialize the seeds for tractography on the cortical surface separating the white and grey matter. Centred around each vertex (node)—in total 20,484—we initialize eight seeds and perform the tractography with the following parameters: fractional anisotropy threshold 0.3, that is, fractional anisotropy <0.3 being termination criteria for the tracking, minimum tract length 20 mm, and maximum angle between two contiguous tracking steps 30°.
Graph representation of the human connectome
The graph representation of the human connectome  is formed by representing the vertices sampled form the surface of grey matter by the nodes
is formed by representing the vertices sampled form the surface of grey matter by the nodes  with n being the total number of nodes (20,484 in this study) and by including the local and long-range connections between the vertices as the edges
with n being the total number of nodes (20,484 in this study) and by including the local and long-range connections between the vertices as the edges  of the graph
of the graph  . Thereby, the local connections correspond to the connections of the vertices on the cortical surface mesh (six connections per vertex to their nearest neighbours) and the long-range connections are determined by the white-matter cortico-cortical and thalamo-cortical fibres. To this end, the nearest vertex of each fibre end point is identified on the grey matter cortical surface and a long-range connection between the two vertices is added for each fibre tract. In this study, we use an undirected, unweighted graph representation leading to the following adjacency matrix:
. Thereby, the local connections correspond to the connections of the vertices on the cortical surface mesh (six connections per vertex to their nearest neighbours) and the long-range connections are determined by the white-matter cortico-cortical and thalamo-cortical fibres. To this end, the nearest vertex of each fibre end point is identified on the grey matter cortical surface and a long-range connection between the two vertices is added for each fibre tract. In this study, we use an undirected, unweighted graph representation leading to the following adjacency matrix:

It is important to note that this graph model of the human connectome differs from the previous studies10,12, in which each node represents one cortical region acquired by a certain parcellation of the cerebral cortex and the edges denote the fibre density between the cortical regions. In contrast to previous graph models of the human connectome, the particular representation used in our study closely approximates the continuous form of the human cortex due to the uniform and dense sampling of the vertices (nodes) from the continuous grey matter cortical surface.
Connectome Laplacian and connectome harmonics
Given the graph representation  of the human connectome, we compute the symmetric graph Laplacian
of the human connectome, we compute the symmetric graph Laplacian  on the connectome graph in order to estimate the discrete counterpart of the Laplace operator23,45 Δ applied to the human connectome, the connectome Laplacian, as:
on the connectome graph in order to estimate the discrete counterpart of the Laplace operator23,45 Δ applied to the human connectome, the connectome Laplacian, as:

where the adjacency matrix A is defined in equation (1) and

denotes the degree matrix of the graph. We then calculate the connectome harmonics  , j∈{1, ⋯, n} by solving the the following eigenvalue problem:
, j∈{1, ⋯, n} by solving the the following eigenvalue problem:

with λj, j∈{1, ⋯, n} being the corresponding eigenvalues of  .
.
Neural field model
Let E(x, t) and I(x, t) correspond to the activity; that is, local spatio-temporal averages of membrane-potentials, of the excitatory and inhibitory neurons at the cortical location  at time t. Following the Wilson–Cowan equations30,35, time evolution of the excitatory and inhibitory neural firing rates satisfy the following non-linear differential equations35:
at time t. Following the Wilson–Cowan equations30,35, time evolution of the excitatory and inhibitory neural firing rates satisfy the following non-linear differential equations35:


where  ,
,  ,
,  and
and  denote the diffusion (spatial propagation) operators of excitatory (E) and inhibitory activities (I), each separately acting on excitatory and inhibitory populations with names (EE, IE) and (EI, II) respectively. Here S denotes the sigmoidal activation function,
denote the diffusion (spatial propagation) operators of excitatory (E) and inhibitory activities (I), each separately acting on excitatory and inhibitory populations with names (EE, IE) and (EI, II) respectively. Here S denotes the sigmoidal activation function,

and τs is a characteristic time scale of the system. We extend the Wilson–Cowan equations to the full structural connectivity of the thalamo-cortical system by incorporating the connectome Laplacian to the diffusion (spatial propagation) terms (Supplementary Notes 1 and 2).
Lypunov stability
We test the robustness of the neural field model for perturbations using Lyapunov stability analysis50. This method involves perturbing the system at some time t* and observing whether the perturbed system converges to the original system. If this is the case, the system may be called Lyapunov stable. As the neural field model is oscillatory for the parameter sets we are concerned with, we must define a measure, which determines the distance between two states. We first perturb the system separately 10 times by white noise at time t*. We then take the absolute value of the difference at each node at each time step and taking the maximum difference. This is known as a L-infinity norm and is commonly used in stability analysis as it looks at the worst case instead of an average case. At each time step we compare all differences across the 10 perturbed systems and again take the worst case. This quantity is defined to be L(t). We plot the distance measure L(t) over time and observe whether L(t)→0 or L(t)→ɛ with ɛ≈0. In Fig. 5(a) we see that L(t)→ɛ and is bounded demonstrating the robustness of the neural field model to noise perturbations.
Additional information
How to cite this article: Atasoy, S. et al. Human brain networks function in connectome-specific harmonic waves. Nat. Commun. 7:10340 doi: 10.1038/ncomms10340 (2016).
References
Laughlin, R. B. Physics, emergence, and the connectome. Neuron 83, 1253–1255 (2014).
Hodgkin, A. L. & Huxley, A. F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117, 500 (1952).
Chialvo, D. R. Emergent complex neural dynamics. Nat. Phys. 6, 744–750 (2010).
Buzsaki, G. Neuronal oscillations in cortical networks. Science 304, 1926–1929 (2004).
Fox, M. D., Snyder, A. Z., Vincent, J. L., Corbetta, M. & Van Essen, D. C. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc. Natl Acad. Sci. USA 102, 9673–9678 (2005).
Fox, M. D. & Raichle, M. E. Spontaneous fluctuations in brain activity observed with functional magnetic resonance imaging. Nat. Rev. Neurosci. 8, 700–711 (2007).
Fox, M. D., Corbetta, M., Snyder, A. Z., Vincent, J. L. & Raichle, M. E. Spontaneous neuronal activity distinguishes human dorsal and ventral attention systems. Proc. Natl Acad. Sci. USA 103, 10046–10051 (2006).
Musso, F., Brinkmeyer, J., Mobascher, A., Warbrick, T. & Winterer, G. Spontaneous brain activity and EEG microstates. a novel EEG/fMRI analysis approach to explore resting-state networks. Neuroimage 52, 1149–1161 (2010).
Britz, J., Van De Ville, D. & Michel, C. M. Bold correlates of EEG topography reveal rapid resting-state network dynamics. Neuroimage 52, 1162–1170 (2010).
Deco, G., Jirsa, V. K. & McIntosh, A. R. Emerging concepts for the dynamical organization of resting-state activity in the brain. Nat. Rev. Neurosci. 12, 43–56 (2011).
Seung, S. Connectome: How the brain’s Wiring makes us who we are Houghton Mifflin Harcourt (2012).
Deco, G., Jirsa, V., McIntosh, A. R., Sporns, O. & Kotter, R. Key role of coupling, delay, and noise in resting brain fluctuations. Proc. Natl Acad. Sci. USA 106, 10302–10307 (2009).
Stewart, I. Mathematics: holes and hot spots. Nature 401, 863–865 (1999).
Chladni, E. F. F. Die Akustik Breitkopf & Härtel (1802).
Roos, C. Quantum physics: simulating magnetism. Nature 484, 461–462 (2012).
Britton, J. W. et al. Engineered two-dimensional Ising interactions in a trapped-ion quantum simulator with hundreds of spins. Nature 484, 489–492 (2012).
Schrödinger, E. An undulatory theory of the mechanics of atoms and molecules. Phys. Rev. 28, 1049 (1926).
Moon, C. R. et al. Quantum phase extraction in isospectral electronic nanostructures. Science 319, 782–787 (2008).
Turing, A. M. The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. B Biol. Sci. 237, 37–72 (1952).
Kondo, S. & Miura, T. Reaction-diffusion model as a framework for understanding biological pattern formation. Science 329, 1616–1620 (2010).
Murray, J. D. How the leopard gets its spots. Sci. Am. 258, 80–87 (1988).
Xu, Y., Vest, C. M. & Murray, J. D. Holographic interferometry used to demonstrate a theory of pattern formation in animal coats. Appl. Opt. 22, 3479–3483 (1983).
Lévy, B. Laplace-Beltrami eigenfunctions towards an algorithm that “understands” geometry. In Int. Conf. Shape Modeling and Applications, 2006.
Reuter, M., Wolter, F.-E. & Peinecke, N. Laplace-beltrami spectra as shape-dnaof surfaces and solids. Comput. Aid. Des. 38, 342–366 (2006).
Belkin, M. & Niyogi, P. Towards a theoretical foundation for Laplacian-based manifold methods. J. Comput. Syst. Sci. 74, 1289–1308 (2008).
Murray, J. Mathematical Biology II: Spatial Models and Biomedical Applications Springer (2003).
Thomas Yeo, B. T. et al. The organization of the human cerebral cortex estimated by intrinsic functional connectivity. J. Neurophysiol. 106, 1125–1165 (2011).
Friston, K. J., Kahan, J., Razi, A., Stephan, K. E. & Sporns, O. On nodes and modes in resting state fMRI. Neuroimage 99, 533–547 (2014).
Isaacson, J. S. & Scanziani, M. How inhibition shapes cortical activity. Neuron 72, 231–243 (2011).
Wilson, H. R. & Cowan, J. D. A mathematical theory of the functional dynamics of cortical and thalamic nervous tissue. Kybernetik 13, 55–80 (1973).
Bressloff, P. C. Spatiotemporal dynamics of continuum neural fields. J. Phys. A: Math. Theor. 45, 033001 (2012).
Swindale, N. A model for the formation of ocular dominance stripes. Proc. R. Soc. Lond. Ser. B. Biol. Sci. 208, 243–264 (1980).
Ermentrout, G. B. & Cowan, J. D. A mathematical theory of visual hallucination patterns. Biol. Cybern. 34, 137–150 (1979).
Rule, M., Stoffregen, M. & Ermentrout, B. A model for the origin and properties of flicker-induced geometric phosphenes. PLoS Comput. Biol. 7, e1002158 (2011).
Ermentrout, G. & Cowan, J. D. Temporal oscillations in neuronal nets. J. Math. Biol. 7, 265–280 (1979).
Ermentrout, G. & Cowan, J. Secondary bifurcation in neuronal nets. SIAM J. Appl. Math. 39, 323–340 (1980).
Kang, K., Shelley, M. & Sompolinsky, H. Mexican hats and pinwheels in visual cortex. Proc. Natl Acad. Sci. USA 100, 2848–2853 (2003).
Jirsa, V. K. Connectivity and dynamics of neural information processing. Neuroinformatics 2, 183–204 (2004).
Cavanaugh, J. R., Bair, W. & Movshon, J. A. Nature and interaction of signals from the receptive field center and surround in macaque v1 neurons. J. Neurophysiol. 88, 2530–2546 (2002).
Webb, B. S., Dhruv, N. T., Solomon, S. G., Tailby, C. & Lennie, P. Early and late mechanisms of surround suppression in striate cortex of macaque. J. Neurosci. 25, 11666–11675 (2005).
Douglas, R. J. & Martin, K. A. Neuronal circuits of the neocortex. Annu. Rev. Neurosci. 27, 419–451 (2004).
Adesnik, H., Bruns, W., Taniguchi, H., Huang, Z. J. & Scanziani, M. A neural circuit for spatial summation in visual cortex. Nature 490, 226–231 (2012).
Haider, B., Häusser, M. & Carandini, M. Inhibition dominates sensory responses in the awake cortex. Nature 493, 97–100 (2013).
Adesnik, H. & Scanziani, M. Lateral competition for cortical space by layer-specific horizontal circuits. Nature 464, 1155–1160 (2010).
Chung, F. R. Spectral Graph Theory, vol. 92, (American Mathematical Soc. (1997).
Izhikevich, E. M. & Edelman, G. M. Large-scale model of mammalian thalamocortical systems. Proc. Natl Acad. Sci. USA 105, 3593–3598 (2008).
Tononi, G. & Koch, C. The neural correlates of consciousness: an update. Ann. N.Y. Acad. Sci. 1124, 239–261 (2008).
Horovitz, S. G. et al. Decoupling of the brain’s default mode network during deep sleep. Proc. Natl Acad. Sci. USA 106, 11376–11381 (2009).
Samann, P. G. et al. Development of the brain’s default mode network from wakefulness to slow wave sleep. Cereb. Cortex 21, 2082–2093 (2011).
Lyapunov, A. M. The general problem of the stability of motion. Int. J. Control 55, 531–534 (1992).
Daunizeau, J., Kiebel, S. J. & Friston, K. J. Dynamic causal modelling of distributed electromagnetic responses. Neuroimage 47, 590–601 (2009).
Hansen, E. C., Battaglia, D., Spiegler, A., Deco, G. & Jirsa, V. K. Functional connectivity dynamics: modeling the switching behavior of the resting state. Neuroimage 105, 525–535 (2015).
de Pasquale, F. et al. Temporal dynamics of spontaneous meg activity in brain networks. Proc. Natl Acad. Sci. USA 107, 6040–6045 (2010).
de Pasquale, F. et al. A cortical core for dynamic integration of functional networks in the resting human brain. Neuron 74, 753–764 (2012).
Spadone, S., de Pasquale, F., Mantini, D. & Della Penna, S. A k-means multivariate approach for clustering independent components from magnetoencephalographic data. Neuroimage 62, 1912–1923 (2012).
Allen, E. A. et al. Tracking whole-brain connectivity dynamics in the resting state. Cereb. Cortex 24, 663–676 (2014).
Hutchison, R. M. et al. Dynamic functional connectivity: promise, issues, and interpretations. Neuroimage 80, 360–378 (2013).
Zalesky, A., Fornito, A., Cocchi, L., Gollo, L. L. & Breakspear, M. Time-resolved resting-state brain networks. Proc. Natl Acad. Sci. USA 111, 10341–10346 (2014).
Leonardi, N. & Van De Ville, D. On spurious and real fluctuations of dynamic functional connectivity during rest. Neuroimage 104, 430–436 (2015).
Basser, P. J., Pajevic, S., Pierpaoli, C., Duda, J. & Aldroubi, A. In vivo fiber tractography using dt-mri data. Magn. Reson. Med. 44, 625–632 (2000).
Acknowledgements
We thank M. Baust, E. Montbrió Fairen, A. Tauste Campo, N. Tsuchiya and C. Clifford for their insightful comments. This work was supported by Australian NHMRC project grants APP1024800, APP1046198 & APP1085404, an ARC grant DP140101560 and a Career Development Fellowship APP1049596 held by J. Pearson. Data used in the preparation of this work were obtained and made available by the Human Connectome Project, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657).
Author information
Authors and Affiliations
Contributions
S.A. and J.P. conceived the study; all authors designed the experiments; S.A. designed and implemented the computation of connectome harmonics and performed the qualitative evaluation; S.A. and I.D. programmed numerical simulations of the neural field model; I.D. performed the linear stability analysis; S.A. and J.P. wrote the manuscript; and all the authors edited the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-10, Supplementary Table 1, Supplementary Notes 1-5, Supplementary Methods, and Supplementary References (PDF 14617 kb)
Supplementary Movie 1
Numerical simulations of the neural field equation for excitatory activity on the graph representation of the human connectome for the diffusion parameters σ EE = 20 , σ EI = 4 ,σ IE = 4 ,σ EE = 50 , where the rest of the parameters were set to the default values( d E = dI = 2 ,α EE =α IE =α EI =α II =150 (MOV 1677 kb)
Supplementary Movie 2
Numerical simulations of the neural field equation for excitatory activity on the graph representation of the human connectome for the diffusion parameters σ EE = 6 , σ EI = 4 ,σ IE = 4 ,σ II = 50 , where the rest of the parameters were set to the default values( d E = dI = 2 ,α EE =α IE =α EI =α II =150) (MOV 1688 kb)
Supplementary Movie 3
Numerical simulations of the neural field equation for excitatory activity on the graph representation of the human connectome for the diffusion parameters σ EE = 6 , σ EI = 4 ,σ IE =10 ,σ II = 50 , where the rest of the parameters were set to the default values( d E = dI = 2 ,α EE =α IE =α EI =α II =150) (MOV 1764 kb)
Supplementary Movie 4
Numerical simulations of the neural field equation for excitatory activity on the graph representation of the human connectome for the diffusion parameters σ EE = 6 , σ EI = 4 ,σ IE =10 ,σ II = 90 , where the rest of the parameters were set to the default values( d E = dI = 2 ,α EE =α IE =α EI =α II =150) (MOV 1717 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Atasoy, S., Donnelly, I. & Pearson, J. Human brain networks function in connectome-specific harmonic waves. Nat Commun 7, 10340 (2016). https://doi.org/10.1038/ncomms10340
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms10340
This article is cited by
-
Eigenmode-based approach reveals a decline in brain structure–function liberality across the human lifespan
Communications Biology (2023)
-
Enhanced brain structure-function tethering in transmodal cortex revealed by high-frequency eigenmodes
Nature Communications (2023)
-
Occipital transcranial direct current stimulation in episodic migraine patients: effect on cerebral perfusion
Scientific Reports (2023)
-
Distributed harmonic patterns of structure-function dependence orchestrate human consciousness
Communications Biology (2023)
-
Intrinsic macroscale oscillatory modes driving long range functional connectivity in female rat brains detected by ultrafast fMRI
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.