Abstract
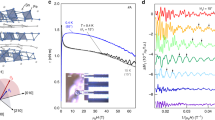
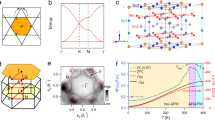
The kagome lattice is a two-dimensional network of corner-sharing triangles1 that is known to host exotic quantum magnetic states2,3,4. Theoretical work has predicted that kagome lattices may also host Dirac electronic states5 that could lead to topological6 and Chern7 insulating phases, but these states have so far not been detected in experiments. Here we study the d-electron kagome metal Fe3Sn2, which is designed to support bulk massive Dirac fermions in the presence of ferromagnetic order. We observe a temperature-independent intrinsic anomalous Hall conductivity that persists above room temperature, which is suggestive of prominent Berry curvature from the time-reversal-symmetry-breaking electronic bands of the kagome plane. Using angle-resolved photoemission spectroscopy, we observe a pair of quasi-two-dimensional Dirac cones near the Fermi level with a mass gap of 30 millielectronvolts, which correspond to massive Dirac fermions that generate Berry-curvature-induced Hall conductivity. We show that this behaviour is a consequence of the underlying symmetry properties of the bilayer kagome lattice in the ferromagnetic state and the atomic spin–orbit coupling. This work provides evidence for a ferromagnetic kagome metal and an example of emergent topological electronic properties in a correlated electron system. Our results provide insight into the recent discoveries of exotic electronic behaviour in kagome-lattice antiferromagnets8,9,10 and may enable lattice-model realizations of fractional topological quantum states11,12.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
O’Keeffe, M. & Hyde, B. G. Crystal Structures. I. Patterns and Symmetry Ch. 5 (Mineralogical Society of America, 1996)
Sachdev, S. Kagome- and triangular-lattice Heisenberg antiferromagnets: ordering from quantum fluctuations and quantum-disordered ground states with unconfined bosonic spinons. Phys. Rev. B 45, 12377–12396 (1992)
Han, T.-H. et al. Fractionalized excitations in the spin-liquid state of a kagome-lattice antiferromagnet. Nature 492, 406–410 (2012)
Zhou, Y., Kanoda, K. & Ng, T.-K. Quantum spin liquid states. Rev. Mod. Phys. 89, 025003 (2017)
Mazin, I. I. et al. Theoretical prediction of a strongly correlated Dirac metal. Nat. Commun. 5, 4261 (2014)
Guo, H.-M. & Franz, M. Topological insulator on the kagome lattice. Phys. Rev. B 80, 113102 (2009)
Xu, G., Lian, B. & Zhang, S.-C. Intrinsic quantum anomalous Hall effect in the kagome lattice Cs2LiMn3F12 . Phys. Rev. Lett. 115, 186802 (2015)
Nakatsuji, S., Kiyohara, N. & Higo, T. Large anomalous Hall effect in a non-collinear antiferromagnet at room temperature. Nature 527, 212–215 (2015)
Nayak, A. K. et al. Large anomalous Hall effect driven by a nonvanishing Berry curvature in the noncolinear antiferromagnet Mn3Ge. Sci. Adv. 2, e1501870 (2016)
Kuroda, K. et al. Evidence for magnetic Weyl fermions in a correlated metal. Nat. Mater. 16, 1090–1095 (2017)
Tang, E. & Wen, X.-G. High-temperature fractional quantum Hall states. Phys. Rev. Lett. 106, 236802 (2011)
Bergholtz, E. J., Liu, Z., Trescher, M., Moessner, R. & Udagawa, M. Topology and interactions in a frustrated slab: tuning from Weyl semimetals to C > 1 fractional Chern insulators. Phys. Rev. Lett. 114, 016806 (2015)
Wallace, P. R. The band theory of graphite. Phys. Rev. 71, 622–634 (1947)
Thouless, D. J., Kohmoto, M., Nightingale, M. P. & den Nijs, M. Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 49, 405–408 (1982)
Chang, C.-Z. et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator. Science 340, 167–170 (2013)
Nagaosa, N., Sinova, J., Onoda, S., MacDonald, A. H. & Ong, N. P. Anomalous Hall effect. Rev. Mod. Phys. 82, 1539–1592 (2010)
Giefers, H. & Nicol, M. High pressure X-ray diffraction study of all FeSn intermetallic compounds and one FeSn solid solution. J. Alloys Compd. 422, 132–144 (2006)
Le Caër, G., Malaman, B. & Roques, B. Mössbauer effect study of Fe3Sn2 . J. Phys. F 8, 323–336 (1978)
Hou, Z. et al. Observation of various and spontaneous magnetic Skyrmionic bubbles at room temperature in a frustrated kagome magnet with uniaxial magnetic anisotropy. Adv. Mater. 29, 1701144 (2017)
Kida, T. et al. The giant anomalous Hall effect in the ferromagnet Fe3Sn2—a frustrated kagome metal. J. Phys. Condens. Matter 23, 112205 (2011)
Wang, Q., Sun, S., Zhang, X., Pang, F. & Lei, H. Anomalous Hall effect in a ferromagnetic Fe3Sn2 single crystal with a geometrically frustrated Fe bilayer kagome lattice. Phys. Rev. B 94, 075135 (2016)
Tian, Y., Ye, L. & Jin, X. Proper scaling of the anomalous Hall effect. Phys. Rev. Lett. 103, 087206 (2009)
Shitade, A. & Nagaosa, N. Anomalous Hall effect in ferromagnetic metals: role of phonons at finite temperature. J. Phys. Soc. Jpn 81, 083704 (2012)
Kim, K. S. et al. Coexisting massive and massless Dirac fermions in symmetry-broken bilayer graphene. Nat. Mater. 12, 887–892 (2013)
Sales, B. C., Saparov, B., McGuire, M. A., Singh, D. J. & Parker, D. S. Ferromagnetism of Fe3Sn and alloys. Sci. Rep. 4, 7024 (2014)
Chen, Y. L. et al. Massive Dirac fermion on the surface of a magnetically doped topological insulator. Science 329, 659–662 (2010)
Xu, S. Y. et al. Hedgehog spin texture and Berry’s phase tuning in a magnetic topological insulator. Nat. Phys. 8, 616–622 (2012)
Balog, R. et al. Bandgap opening in graphene induced by patterned hydrogen adsorption. Nat. Mater. 9, 315–319 (2010)
Ishii, Y., Harima, H., Okamoto, Y., Yamaura, J. & Hiroi, Z. YCr6Ge6 as a candidate compound for a kagome metal. J. Phys. Soc. Jpn 82, 023705 (2013)
Kane, C. L. & Mele, E. J. Quantum spin Hall effect in graphene. Phys. Rev. Lett. 95, 226801 (2005)
Haldane, F. D. M. Model for a quantum Hall effect without Landau levels: condensed-matter realization of the “parity anomaly”. Phys. Rev. Lett. 61, 2015–2018 (1988)
Drijver, J. W., Sinnema, S. G. & van der Woude, F. Magnetic properties of hexagonal and cubic Fe3Ge. J. Phys. F 6, 2165–2177 (1976)
Fenner, L. A., Dee, A. A. & Wills, A. S. Non-collinearity and spin frustration in the itinerant kagome ferromagnet Fe3Sn2 . J. Phys. Condens. Matter 21, 452202 (2009)
Raquet, B., Viret, M., Sondergard, E., Cespedes, O. & Mamy, R. Electron-magnon scattering and magnetic resistivity in 3d ferromagnets. Phys. Rev. B 66, 024433 (2002)
Richard, P. et al. Observation of Dirac cone electronic dispersion in BaFe2As2 . Phys. Rev. Lett. 104, 137001 (2010)
Tan, S. Y. et al. Observation of Dirac cone band dispersions in FeSe thin films by photoemission spectroscopy. Phys. Rev. B 93, 104513 (2016)
Bostwick, A., Ohta, T., Seyller, T., Horn, K. & Rotenberg, E. Quasiparticle dynamics in graphene. Nat. Phys. 3, 36–40 (2007)
Nevius, M. S. et al. Semiconducting graphene from highly ordered substrate interactions. Phys. Rev. Lett. 115, 136802 (2015)
Damascelli, A., Hussain, Z. & Shen, Z.-X. Angle-resolved photoemission studies of the cuprate superconductors. Rev. Mod. Phys. 75, 473–541 (2003)
Onose, Y. et al. Observation of the magnon Hall effect. Science 329, 297–299 (2010)
Chisnell, R. et al. Topological magnon bands in a kagome lattice ferromagnet. Phys. Rev. Lett. 115, 147201 (2015)
Inami, T., Nishiyama, M., Maegawa, S. & Oka, Y. Magnetic structure of the kagome lattice antiferromagnet potassium jarosite KFe3(OH)6(SO4)2 . Phys. Rev. B 61, 12181–12186 (2000)
Hiroi, Z. et al. Spin-1/2 kagome-like lattice in volborthite Cu3V2O7(OH)2 ∙ 2H2O. J. Phys. Soc. Jpn 70, 3377–3384 (2001)
Qi, X. L., Wu, Y.-S. & Zhang, S.-C. Topological quantization of the spin Hall effect in two-dimensional paramagnetic semiconductors. Phys. Rev. B 74, 085308 (2006)
Sinitsyn, N. A., MacDonald, A. H., Jungwirth, T., Dugaev, V. K. & Sinova, J. Anomalous Hall effect in a two-dimensional Dirac band: the link between the Kubo-Streda formula and the semiclassical Boltzmann equation approach. Phys. Rev. B 75, 045315 (2007)
Haldane, F. D. M. Berry curvature on the Fermi surface: anomalous Hall effect as a topological Fermi-liquid property. Phys. Rev. Lett. 93, 206602 (2004)
Fang, Z. et al. The anomalous Hall effect and magnetic monopoles in momentum space. Science 302, 92–95 (2003)
Acknowledgements
We are grateful to X.-G. Wen and E. Tang for discussions. This research was funded in part by the Gordon and Betty Moore Foundation EPiQS Initiative, grant GBMF3848 to J.G.C. and NSF grant DMR-1554891. L.Y., J.L. and F.v.C. acknowledge support by the STC Center for Integrated Quantum Materials, NSF grant number DMR-1231319. L.Y. acknowledges support by the Tsinghua Education Foundation. M.K. acknowledges a Samsung Scholarship from the Samsung Foundation of Culture. This research used resources of the Advanced Light Source, which is a DOE Office of Science User Facility under contract number DE-AC02-05CH11231. A portion of this work was performed at the National High Magnetic Field Laboratory, which is supported by NSF cooperative agreement number DMR-1157490, the State of Florida and the US Department of Energy.
Author information
Authors and Affiliations
Contributions
L.Y., T.S. and C.R.W. grew the single crystals. L.Y. characterized the materials, performed the transport and magnetic measurements and analysed the resultant data. M.K., C.J., A.B. and E.R. performed the ARPES experiment and analysed the resultant data. J.L. and L.Y. performed the theoretical calculations. F.v.C. and D.C.B. performed the electron microscopy study. All authors contributed to writing the manuscript. L.F., R.C. and J.G.C. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Reviewer Information Nature thanks E. Bergholtz, B. Lake and O. Rader for their contribution to the peer review of this work.
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Figure 1 Metallic transport in Fe3Sn2.
a, Resistivity ρ as a function of temperature T in the kagome plane for Fe3Sn2 sample C1. The inset shows a photograph of Fe3Sn2 single crystals. b, c, Magnetoresistance (defined as MR = [ρxx(B) − ρxx(0)]/ρxx(0)) at selected T with B applied perpendicular (b) or parallel (c) to the kagome plane and B ⊥ I (schematics of the configurations are shown as insets).
Extended Data Figure 2 Extracting anomalous Hall conductivity and high-field transport.
a, In-plane Hall conductivity σxy as a function of magnetic induction B at selected temperatures. Dashed lines represent the linear fit to  . The data at 2 K and 50 K have been scaled by the factors shown for clarity. b, Magnetoresistance (main panel) and Hall effect (inset) of Fe3Sn2 with applied magnetic field μ0H ‖ c up to 31 T.
. The data at 2 K and 50 K have been scaled by the factors shown for clarity. b, Magnetoresistance (main panel) and Hall effect (inset) of Fe3Sn2 with applied magnetic field μ0H ‖ c up to 31 T.
Extended Data Figure 3 Momentum and energy-dependent band structure along high-symmetry directions.
a, e, Fermi surface of Fe3Sn2 obtained from different experimental geometries. b–d, f, g, Band dispersion of Fe3Sn2 along high-symmetry directions. The panels correspond to the momentum directions along the red (b), orange (c), green (d), magenta (f) and purple (g) dotted lines in a and e. The inset in d shows the raw data of Fig. 3c (with the same energy and momentum range), highlighting the spectral weight distribution near the Dirac points. h, Energy distribution curves at different K points indicated in c, d, f and g. The curves are shifted along the vertical direction for clarity. The inset shows an example of Gaussian fits; the extracted gap size is Δ = 30 ± 5 meV.
Extended Data Figure 4 Photon-energy dependence of ARPES spectra.
ARPES intensity plot for Fe3Sn2 taken along the Γ–K direction as a function of binding energy k and photon energy.
Extended Data Figure 5 Berry curvature and Hall conductivity for a massive Dirac fermion.
a–c, Schematics of 2D Dirac fermions and the corresponding Bloch-sphere representation of the wavefunction of filled states for the gapless case (a) and the gapped case with EF in (b) and out of (c) the gap. d, Fermi energy EF dependence of σxy for the case of a single massive Dirac fermion with gap Δ and Fermi velocity vF.
Rights and permissions
About this article
Cite this article
Ye, L., Kang, M., Liu, J. et al. Massive Dirac fermions in a ferromagnetic kagome metal. Nature 555, 638–642 (2018). https://doi.org/10.1038/nature25987
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature25987
This article is cited by
-
Distinct switching of chiral transport in the kagome metals KV3Sb5 and CsV3Sb5
npj Quantum Materials (2024)
-
Correlated order at the tipping point in the kagome metal CsV3Sb5
Nature Physics (2024)
-
Spin Berry curvature-enhanced orbital Zeeman effect in a kagome metal
Nature Physics (2024)
-
Anomalous electrons in a metallic kagome ferromagnet
Nature (2024)
-
Phonon promoted charge density wave in topological kagome metal ScV6Sn6
Nature Communications (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.