Abstract
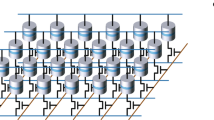
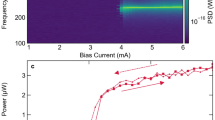
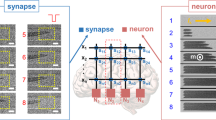
Neurons in the brain behave as nonlinear oscillators, which develop rhythmic activity and interact to process information1. Taking inspiration from this behaviour to realize high-density, low-power neuromorphic computing will require very large numbers of nanoscale nonlinear oscillators. A simple estimation indicates that to fit 108 oscillators organized in a two-dimensional array inside a chip the size of a thumb, the lateral dimension of each oscillator must be smaller than one micrometre. However, nanoscale devices tend to be noisy and to lack the stability that is required to process data in a reliable way. For this reason, despite multiple theoretical proposals2,3,4,5 and several candidates, including memristive6 and superconducting7 oscillators, a proof of concept of neuromorphic computing using nanoscale oscillators has yet to be demonstrated. Here we show experimentally that a nanoscale spintronic oscillator (a magnetic tunnel junction)8,9 can be used to achieve spoken-digit recognition with an accuracy similar to that of state-of-the-art neural networks. We also determine the regime of magnetization dynamics that leads to the greatest performance. These results, combined with the ability of the spintronic oscillators to interact with each other, and their long lifetime and low energy consumption, open up a path to fast, parallel, on-chip computation based on networks of oscillators.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Buzsaki, G. Rhythms of the Brain (Oxford Univ. Press, 2011)
Hoppensteadt, F. C. & Izhikevich, E. M. Oscillatory neurocomputers with dynamic connectivity. Phys. Rev. Lett. 82, 2983–2986 (1999)
Aonishi, T., Kurata, K. & Okada, M. Statistical mechanics of an oscillator associative memory with scattered natural frequencies. Phys. Rev. Lett. 82, 2800–2803 (1998)
Jaeger, H. & Haas, H. Harnessing nonlinearity: predicting chaotic systems and saving energy in wireless communication. Science 304, 78–80 (2004)
Maass, W., Natschläger, T. & Markram, H. Real-time computing without stable states: a new framework for neural computation based on perturbations. Neural Comput. 14, 2531–2560 (2002)
Pickett, M. D., Medeiros-Ribeiro, G. & Williams, R. S. A scalable neuristor built with Mott memristors. Nat. Mater. 12, 114–117 (2013)
Segall, K. et al. Synchronization dynamics on the picosecond time scale in coupled Josephson junction neurons. Phys. Rev. E 95, 032220 (2017)
Kiselev, S. I. et al. Microwave oscillations of a nanomagnet driven by a spin-polarized current. Nature 425, 380–383 (2003)
Rippard, W. H., Pufall, M. R., Kaka, S., Russek, S. E. & Silva, T. J. Direct-current induced dynamics in Co90Fe10/Ni80Fe20 point contacts. Phys. Rev. Lett. 92, 027201 (2004)
Slonczewski, J. C. Current-driven excitation of magnetic multilayers. J. Magn. Magn. Mater. 159, L1–L7 (1996)
Berger, L. Emission of spin waves by a magnetic multilayer traversed by a current. Phys. Rev. B 54, 9353–9358 (1996)
Tsunegi, S., Yakushiji, K., Fukushima, A., Yuasa, S. & Kubota, H. Microwave emission power exceeding 10 μW in spin torque vortex oscillator. Appl. Phys. Lett. 109, 252402 (2016)
Sato, H. et al. Properties of magnetic tunnel junctions with a MgO/CoFeB/Ta/CoFeB/MgO recording structure down to junction diameter of 11 nm. Appl. Phys. Lett. 105, 062403 (2014)
Apalkov, D., Dieny, B. & Slaughter, J. M. Magnetoresistive random access memory. Proc. IEEE 104, 1796–1830 (2016)
Slavin, A. & Tiberkevich, V. Nonlinear auto-oscillator theory of microwave generation by spin-polarized current. IEEE Trans. Magn. 45, 1875–1918 (2009)
Houshang, A. et al. Spin-wave-beam driven synchronization of nanocontact spin-torque oscillators. Nat. Nanotechnol. 11, 280–286 (2016)
Macià, F., Kent, A. D. & Hoppensteadt, F. C. Spin-wave interference patterns created by spin-torque nano-oscillators for memory and computation. Nanotechnology 22, 095301 (2011)
Pufall, M. R. et al. Physical implementation of coherently coupled oscillator networks. IEEE J. Explor. Solid-State Comput. Devices Circuits 1, 76–84 (2015)
Nikonov, D. E. et al. Coupled-oscillator associative memory array operation for pattern recognition. IEEE J. Explor. Solid-State Comput. Devices Circuits 1, 85–93 (2015)
Yogendra, K., Fan, D. & Roy, K. Coupled spin torque nano oscillators for low power neural computation. IEEE Trans. Magn. 51, 4003909 (2015)
Grollier, J., Querlioz, D. & Stiles, M. D. Spintronic nanodevices for bioinspired computing. Proc. IEEE 104, 2024–2039 (2016)
Grimaldi, E. et al. Response to noise of a vortex based spin transfer nano-oscillator. Phys. Rev. B 89, 104404 (2014)
Soriano, M. C. et al. Delay-based reservoir computing: noise effects in a combined analog and digital implementation. IEEE Trans. Neural Netw. Learn. Syst. 26, 388–393 (2015)
Appeltant, L. et al. Information processing using a single dynamical node as complex system. Nat. Commun. 2, 468 (2011)
Paquot, Y. et al. Optoelectronic reservoir computing. Sci. Rep. 2, 287 (2012)
Martinenghi, R., Rybalko, S., Jacquot, M., Chembo, Y. K. & Larger, L. Photonic nonlinear transient computing with multiple-delay wavelength dynamics. Phys. Rev. Lett. 108, 244101 (2012)
Texas Instruments. 46-Word Speaker-Dependent Isolated Word Corpus (TI-46), NIST Speech Disc 7-1.1, https://catalog.ldc.upenn.edu/LDC93S9 (NIST, 1991)
LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015)
Yildiz, I. B., von Kriegstein, K. & Kiebel, S. J. From birdsong to human speech recognition: Bayesian inference on a hierarchy of nonlinear dynamical systems. PLOS Comput. Biol. 9, e1003219 (2013)
Lyon, R. A computational model of filtering, detection, and compression in the cochlea. in IEEE Int. Conf. Acoustics, Speech, and Signal Processing (ICASSP 82) Vol. 7, 1282–1285 (IEEE, 1982)
Acknowledgements
This work was supported by the European Research Council (ERC) under grant bioSPINspired 682955. We thank L. Larger, B. Penkovsky and F. Duport for discussions.
Author information
Authors and Affiliations
Contributions
The study was designed by J.G. and M.D.S., samples were optimized and fabricated by S.T. and K.Y., experiments were performed by J.T. and M.R., numerical studies were realized by F.A.A., M.R. and G.K., and all authors contributed to analysing the results and writing the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Reviewer Information Nature thanks F. Hoppensteadt and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Torrejon, J., Riou, M., Araujo, F. et al. Neuromorphic computing with nanoscale spintronic oscillators. Nature 547, 428–431 (2017). https://doi.org/10.1038/nature23011
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature23011
This article is cited by
-
Nonlinear dynamics of directly coupled skyrmions in ferrimagnetic spin torque nano-oscillators
npj Computational Materials (2024)
-
Task-adaptive physical reservoir computing
Nature Materials (2024)
-
Universal scaling between wave speed and size enables nanoscale high-performance reservoir computing based on propagating spin-waves
npj Spintronics (2024)
-
In-sensor human gait analysis with machine learning in a wearable microfabricated accelerometer
Communications Engineering (2024)
-
Physical reservoir computing with emerging electronics
Nature Electronics (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.