Abstract
Processes such as the scattering of alpha particles (4He), the triple-alpha reaction, and alpha capture play a major role in stellar nucleosynthesis. In particular, alpha capture on carbon determines the ratio of carbon to oxygen during helium burning, and affects subsequent carbon, neon, oxygen, and silicon burning stages. It also substantially affects models of thermonuclear type Ia supernovae, owing to carbon detonation in accreting carbon–oxygen white-dwarf stars1,2,3. In these reactions, the accurate calculation of the elastic scattering of alpha particles and alpha-like nuclei—nuclei with even and equal numbers of protons and neutrons—is important for understanding background and resonant scattering contributions. First-principles calculations of processes involving alpha particles and alpha-like nuclei have so far been impractical, owing to the exponential growth of the number of computational operations with the number of particles. Here we describe an ab initio calculation of alpha–alpha scattering that uses lattice Monte Carlo simulations. We use lattice effective field theory to describe the low-energy interactions of protons and neutrons, and apply a technique called the ‘adiabatic projection method’ to reduce the eight-body system to a two-cluster system. We take advantage of the computational efficiency and the more favourable scaling with system size of auxiliary-field Monte Carlo simulations to compute an ab initio effective Hamiltonian for the two clusters. We find promising agreement between lattice results and experimental phase shifts for s-wave and d-wave scattering. The approximately quadratic scaling of computational operations with particle number suggests that it should be possible to compute alpha scattering and capture on carbon and oxygen in the near future. The methods described here can be applied to ultracold atomic few-body systems as well as to hadronic systems using lattice quantum chromodynamics to describe the interactions of quarks and gluons.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Imbriani, G. et al. The 12C(α, γ )16O reaction rate and the evolution of stars in the mass range 0.8 ≤ M/M⊙ ≤ 25. Astrophys. J. 558, 903–915 (2001)
Rauscher, T., Heger, A., Hoffman, R. D. & Woosley, S. E. Nucleosynthesis in massive stars with improved nuclear and stellar physics. Astrophys. J. 576, 323–348 (2002)
Wiescher, M., Käppeler, F. & Langanke, K. Critical reactions in contemporary nuclear astrophysics. Annu. Rev. Astron. Astrophys. 50, 165–210 (2012)
Nollett, K. M., Pieper, S. C., Wiringa, R. B., Carlson, J. & Hale, G. M. Quantum Monte Carlo calculations of neutron-α scattering. Phys. Rev. Lett. 99, 022502 (2007)
Quaglioni, S. & Navrátil, P. Ab initio many-body calculations of n-3H, n-4He, p-3,4He, and n-10Be scattering. Phys. Rev. Lett. 101, 092501 (2008)
Navrátil, P. & Quaglioni, S. Ab initio many-body calculations of the 3H(d, n)4He and 3He(d, p)4He fusion. Phys. Rev. Lett. 108, 042503 (2012)
Hagen, G. & Michel, N. Elastic proton scattering of medium mass nuclei from coupled-cluster theory. Phys. Rev. C 86, 021602(R) (2012)
Orlandini, G. et al. Coupling the Lorentz integral transform (LIT) and the coupled cluster (CC) methods: a way towards continuum spectra of “not-so-few-body” systems. Few-Body Syst. 55, 907–911 (2014)
Woosley, S. E., Arnett, W. D. & Clayton, D. D. The explosive burning of oxygen and silicon. Astrophys. J. Suppl. Ser. 26, 231–312 (1973)
Epelbaum, E., Krebs, H., Lee, D. & Meißner, U.-G. Ab initio calculation of the Hoyle state. Phys. Rev. Lett. 106, 192501 (2011)
Epelbaum, E., Krebs, H., Lähde, T., Lee, D. & Meißner, U.-G. Structure and rotations of the Hoyle state. Phys. Rev. Lett. 109, 252501 (2012)
Lähde, T. A. et al. Nuclear lattice simulations using symmetry-sign extrapolation. Eur. Phys. J. A 51, 92 (2015)
Rupak, G. & Lee, D. Radiative capture reactions in lattice effective field theory. Phys. Rev. Lett. 111, 032502 (2013)
Pine, M., Lee, D. & Rupak, G. Adiabatic projection method for scattering and reactions on the lattice. Eur. Phys. J. A 49, 151 (2013)
Elhatisari, S. & Lee, D. Fermion-dimer scattering using an impurity lattice Monte Carlo approach and the adiabatic projection method. Phys. Rev. C 90, 064001 (2014)
Rupak, G. & Ravi, P. Proton–proton fusion in lattice effective field theory. Phys. Lett. B 741, 301–304 (2014)
Rokash, A. et al. Scattering cluster wave functions on the lattice using the adiabatic projection method. Phys. Rev. C 92, 054612 (2015)
Epelbaum, E., Hammer, H.-W. & Meißner, U.-G. Modern theory of nuclear forces. Rev. Mod. Phys. 81, 1773–1825 (2009)
Heydenburg, N. P. & Temmer, G. M. Alpha-alpha scattering at low energies. Phys. Rev. 104, 123–134 (1956)
Nilson, R., Jentschke, W. K., Briggs, G. R., Kerman, R. O. & Snyder, J. N. Investigation of excited states in Be8 by alpha-particle scattering from He. Phys. Rev. 109, 850–860 (1958)
Tombrello, T. A. & Senhouse, L. S. Elastic scattering of alpha particles from helium. Phys. Rev. 129, 2252–2258 (1963)
Afzal, S. A., Ahmad, A. A. Z. & Ali, S. Systematic survey of the α–α interaction. Rev. Mod. Phys. 41, 247–273 (1969)
Lu, B.-N., Lähde, T. A., Lee, D. & Meißner, U.-G. Precise determination of lattice phase shifts and mixing angles. Preprint at http://arxiv.org/abs/1506.05652 (2015)
Lee, D. Lattice simulations for few- and many-body systems. Prog. Part. Nucl. Phys. 63, 117–154 (2009)
Borasoy, B., Epelbaum, E., Krebs, H., Lee, D. & Meißner, U.-G. Two-particle scattering on the lattice: phase shifts, spin-orbit coupling, and mixing angles. Eur. Phys. J. A 34, 185–196 (2007)
Higa, R., Hammer, H.-W. & van Kolck, U. αα scattering in halo effective field theory. Nucl. Phys. A 809, 171–188 (2008)
Chen, J.-W., Lee, D. & Schaefer, T. Inequalities for light nuclei in the Wigner symmetry limit. Phys. Rev. Lett. 93, 242302 (2004)
Avila, M. L. et al. Constraining the 6.05 MeV 0+ and 6.13 MeV 3− cascade transitions in the 12C(α, γ)16O reaction using the asymptotic normalization coefficients. Phys. Rev. Lett. 114, 071101 (2015)
Schürmann, D., Gialanella, L., Kunz, R. & Strieder, F. The astrophysical S factor of 12C(α, γ)16O at stellar energy. Phys. Lett. B 711, 35–40 (2012)
Zhang, X., Nollett, K. M. & Phillips, D. R. Combining ab initio calculations and low-energy effective field theory for halo nuclear systems: the case of 7Be + p → 8B + γ. Phys. Rev. C 89, 051602(R) (2014)
Epelbaum, E., Krebs, H., Lee, D. & Meißner, U.-G. Lattice calculations for A = 3, 4, 6, 12 nuclei using chiral effective field theory. Eur. Phys. J. A 45, 335–352 (2010)
Hubbard, J. Calculation of partition functions. Phys. Rev. Lett. 3, 77–78 (1959)
Stratonovich, R. L. On a method of calculating quantum distribution functions. Sov. Phys. Dokl. 2, 416–419 (1958)
Koonin, S. E. Auxiliary-field Monte Carlo methods. J. Stat. Phys. 43, 985–990 (1986)
Lee, D. Spectral convexity for attractive SU(2N) fermions. Phys. Rev. Lett. 98, 182501 (2007)
Wigner, E. On the consequences of the symmetry of the nuclear hamiltonian on the spectroscopy of nuclei. Phys. Rev. 51, 106–119 (1937)
Mehen, T., Stewart, I. W. & Wise, M. B. Wigner symmetry in the limit of large scattering lengths. Phys. Rev. Lett. 83, 931–934 (1999)
Kaplan, D. B. & Savage, M. J. The spin-flavor dependence of nuclear forces from large-N QCD. Phys. Lett. B 365, 244–251 (1996)
Calle Cordón, A. & Ruiz Arriola, E. Wigner symmetry, large N c and renormalized one-boson exchange potential. Phys. Rev. C 78, 054002 (2008)
Beane, S. et al. Nucleon-nucleon scattering parameters in the limit of SU(3) flavor symmetry. Phys. Rev. C 88, 024003 (2013)
Beane, S. R. et al. Ab initio calculation of the np → dγ radiative capture process. Phys. Rev. Lett. 115, 132001 (2015)
Scalettar, R. T., Scalapino, D. J. & Sugar, R. L. New algorithm for the numerical simulation of fermions. Phys. Rev. B 34, 7911–7917 (1986)
Gottlieb, S., Liu, W., Toussaint, D., Renken, R. L. & Sugar, R. L. Hybrid molecular dynamics algorithms for the numerical simulation of quantum chromodynamics. Phys. Rev. D 35, 2531–2542 (1987)
Duane, S., Kennedy, A. D., Pendleton, B. J. & Roweth, D. Hybrid Monte Carlo. Phys. Lett. B 195, 216–222 (1987)
Carlson, J., Pandharipande, V. & Wiringa, R. Variational calculations of resonant states in 4He. Nucl. Phys. A 424, 47–59 (1984)
Kong, X. & Ravndal, F. Coulomb effects in low-energy proton proton scattering. Nucl. Phys. A 665, 137–163 (2000)
Rupak, G. & Kong, X.-w. Quartet S-wave p–d scattering in EFT. Nucl. Phys. A 717, 73–90 (2003)
Bethe, H. A. Theory of the effective range in nuclear scattering. Phys. Rev. 76, 38–50 (1949)
Jackson, J. D. & Blatt, J. M. The interpretation of low energy proton-proton scattering. Rev. Mod. Phys. 22, 77–118 (1950)
König, S., Lee, D. & Hammer, H.-W. Causality constraints for charged particles. J. Phys. G 40, 045106 (2013)
Tilley, D. R. et al. Energy levels of light nuclei A = 8, 9, 10. Nucl. Phys. A 745, 155–362 (2004)
Hoop, B., Hale, G. M. & Navratil, P. Neutron-4He resonant scattering at d-3H threshold. Preprint at http://arxiv.org/abs/1111.0985 (2011)
Orlov, Yu. V., Irgaziev, B. F. & Nikitina, L. I. Asymptotic normalization coefficients of resonant and bound states from the phase shifts for αα and α12C scattering. Preprint at http://arxiv.org/abs/1508.07538 (2015)
Hupin, G., Quaglioni, S. & Navrátil, P. Predictive theory for elastic scattering and recoil of protons from 4He. Phys. Rev. C 90, 061601(R) (2014)
Page, P. R. & Hale, G. M. 8Be nuclear data evaluation. AIP Conf. Proc. 769, 390–393 (2005)
Gazit, D., Quaglioni, S. & Navrátil, P. Three-nucleon low-energy constants from the consistency of interactions and currents in chiral effective field theory. Phys. Rev. Lett. 103, 102502 (2009)
Klein, N., Lee, D., Liu, W. & Meißner, U.-G. Regularization methods for nuclear lattice effective field theory. Phys. Lett. B 747, 511–516 (2015)
Lu, B.-N., Lähde, T. A., Lee, D. & Meißner, U.-G. Breaking and restoration of rotational symmetry on the lattice for bound state multiplets. Phys. Rev. D 90, 034507 (2014)
Lu, B.-N., Lähde, T. A., Lee, D. & Meißner, U.-G. Breaking and restoration of rotational symmetry for irreducible tensor operators on the lattice. Phys. Rev. D 92, 014506 (2015)
Yamazaki, T., Ishikawa, K.-i., Kuramashi, Y. & Ukawa, A. Helium nuclei, deuteron and dineutron in 2 + 1 flavor lattice QCD. Phys. Rev. D 86, 074514 (2012)
Berkowitz, E. et al. Two-nucleon higher partial-wave scattering from lattice QCD. Preprint at http://arxiv.org/abs/1508.00886 (2015)
Chang, E. et al. The magnetic structure of light nuclei from lattice QCD. Preprint at http://arxiv.org/abs/1506.05518 (2015)
Epelbaum, E., Krebs, H., Lee, D. & Meißner, U.-G. Lattice effective field theory calculations for A = 3, 4, 6, 12 nuclei. Phys. Rev. Lett. 104, 142501 (2010)
Lähde, T. A. et al. Lattice effective field theory for medium-mass nuclei. Phys. Lett. B 732, 110–115 (2014)
Epelbaum, E., Krebs, H., Lee, D. & Meißner, U.-G. Ground state energy of dilute neutron matter at next-to-leading order in lattice chiral effective field theory. Eur. Phys. J. A 40, 199–213 (2009)
Wlazłowski, G., Holt, J. W., Moroz, S., Bulgac, A. & Roche, K. J. Auxiliary-field quantum Monte Carlo simulations of neutron matter in chiral effective field theory. Phys. Rev. Lett. 113, 182503 (2014)
Rupak, G. & Higa, R. Model-independent calculation of radiative neutron capture on lithium-7. Phys. Rev. Lett. 106, 222501 (2011)
Acharya, B. & Phillips, D. R. 19Carbon in halo EFT: effective-range parameters from Coulomb-dissociation experiments. Nucl. Phys. A 913, 103–115 (2013)
Ji, C., Elster, C. & Phillips, D. R. 6He nucleus in halo effective field theory. Phys. Rev. C 90, 044004 (2014)
Ryberg, E., Forssén, C., Hammer, H.-W. & Platter, L. Constraining low-energy proton capture on beryllium-7 through charge radius measurements. Eur. Phys. J. A 50, 170 (2014)
Acknowledgements
We acknowledge discussions with G. Hale and partial financial support from the Deutsche Forschungsgemeinschaft (Sino-German CRC 110), the Helmholtz Association (contract no. VH-VI-417), BMBF (grant no. 05P12PDFTE), the US Department of Energy (DE-FG02-03ER41260), and US National Science Foundation grant no. PHY-1307453. Further support was provided by the EU HadronPhysics3 project, the ERC project no. 259218 NUCLEAREFT, and the Magnus Ehrnrooth Foundation of the Finnish Society of Sciences and Letters. The computational resources were provided by the Jülich Supercomputing Centre at Forschungszentrum Jülich and by RWTH Aachen.
Author information
Authors and Affiliations
Contributions
S.E. performed the analysis of the scattering data. S.E., E.E., H.K., D.L., and G.R. were involved in conceptual development of the adiabatic projection method. S.E. and T.L. produced the figures. T.A.L., D.L., T.L., and U.-G.M. obtained supercomputing time and developed the code. All authors were involved in writing, editing, and reviewing the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Extended data figures and tables
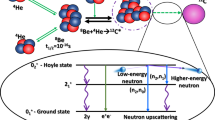
Extended Data Figure 1 Schematic overview of our method.
We start with an eight-body system of protons and neutrons. Each alpha-particle wave packet consists of four nucleons. The protons are red, the neutrons are blue, and the spins are represented by arrows. Next, we perfom ab initio lattice Monte Carlo simulations to construct the adiabatic Hamiltonian for two alpha clusters (grey spheres). Finally, we use the adiabatic Hamiltonian to compute alpha–alpha scattering phase shifts.
Extended Data Figure 2 s-wave extrapolations at NNLO.
a–g, NNLO results (circles) for the s-wave phase shift δ0 versus Lt at laboratory energy ELab = 1.00 MeV, 2.00 MeV, 3.00 MeV, 6.96 MeV, 8.87 MeV, 10.88 MeV, and 12.30 MeV, respectively, as labelled. The theoretical error bars indicate 1 s.d. uncertainty due to Monte Carlo errors. The dot-dashed lines are fits to the data, used to extrapolate the Lt → ∞ limits. The red hatched regions indicate the 1 s.d. error estimate of the extrapolation.
Extended Data Figure 3 d-wave extrapolations at NNLO.
a–g, NNLO results (circles) for the d-wave phase shift δ2 versus Lt at laboratory energy ELab = 2.00 MeV, 3.00 MeV, 5.26 MeV, 6.96 MeV, 8.87 MeV, 9.88 MeV, and 10.88 MeV, respectively, as labelled. The theoretical error bars indicate 1 s.d. uncertainty due to Monte Carlo errors. The dot-dashed lines are fits to the data, used to extrapolate the Lt → ∞ limits. The red hatched regions indicate the 1 s.d. error estimate of the extrapolation.
Rights and permissions
About this article
Cite this article
Elhatisari, S., Lee, D., Rupak, G. et al. Ab initio alpha–alpha scattering. Nature 528, 111–114 (2015). https://doi.org/10.1038/nature16067
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature16067
This article is cited by
-
Perspectives on Few-Body Cluster Structures in Exotic Nuclei
Few-Body Systems (2023)
-
Alpha-alpha scattering in the Multiverse
Journal of High Energy Physics (2022)
-
Local Two- and Three-Nucleon Chiral Interactions
Few-Body Systems (2021)
-
Chiral Effective Field Theory after Thirty Years: Nuclear Lattice Simulations
Few-Body Systems (2021)
-
The Fredholm determinant for Hulthén-distorted non-local separable potential: Application to \( \alpha {-}\alpha \) elastic scattering
Pramana (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.