Main

Neutron stars are extreme astrophysical objects whose interiors may contain exotic new forms of matter. The structure and size of neutron stars are linked to the thickness of the neutron skin in atomic nuclei via the neutron-matter equation of state1,2,3. The nucleus 208Pb is an attractive target for exploring this link in both experimental4,5 and theoretical2,6,7 studies owing to the large excess of neutrons and its simple structure. Mean-field calculations predict a wide range for Rskin(208Pb) because the isovector parts of nuclear energy density functionals are not well constrained by binding energies and charge radii2,7,8,9. Additional constraints may be obtained10 by including the electric dipole polarizability of 208Pb, though this comes with a model dependence11 which is difficult to quantify. In general, the estimation of systematic theoretical uncertainties is a challenge for mean-field theory.

In contrast, precise ab initio computations, which provide a path to comprehensive uncertainty estimation, have been accomplished for the neutron-matter equation of state12,13,14 and the neutron skin in the medium-mass nucleus 48Ca (ref. 15). However, up to now, treating 208Pb within the same framework was out of reach. Owing to breakthrough developments in quantum many-body methods, such computations are now becoming feasible for heavy nuclei16,17,18,19. The ab initio computation of 208Pb we report herein represents a significant step in mass number from the previously computed tin isotopes16,17 (Fig. 1). The complementary statistical analysis in this work is enabled by emulators (for mass number A ≤ 16) which mimic the outputs of many-body solvers but are orders of magnitude faster.

Fig. 1: Trend of realistic ab initio computations for the nuclear A-body problem.
figure 1

The bars highlight the years of the first realistic computations of doubly magic nuclei. The height of each bar corresponds to the mass number A divided by the logarithm of the total compute power RTOP500 (in flops s−1) of the pertinent TOP500 list45. This ratio would be approximately constant if progress were solely due to exponentially increasing computing power. However, algorithms which instead scale polynomially in A have greatly increased the reach.

Source data

Full size image

In this paper, we develop a unified ab initio framework to link the physics of nucleon–nucleon scattering and few-nucleon systems to properties of medium- and heavy-mass nuclei up to 208Pb, and ultimately to the nuclear-matter equation of state near saturation density.

Linking models to reality

Our approach to constructing nuclear interactions is based on chiral effective field theory (EFT)20,21,22. In this theory, the long-range part of the strong nuclear force is known and stems from pion exchanges, while the unknown short-range contributions are represented as contact interactions; we also include the Δ isobar degree of freedom23. At next-to-next-to leading order in Weinberg’s power counting, the four pion–nucleon low-energy constants (LECs) are tightly fixed from pion–nucleon scattering data24. The 13 additional LECs in the nuclear potential must be constrained from data.

We use history matching25,26 to explore the modelling capabilities of ab initio methods by identifying a non-implausible region in the vast parameter space of LECs, for which the model output yields acceptable agreement with selected low-energy experimental data (denoted herein as history-matching observables). The key to efficiently analyse this high-dimensional parameter space is the use of emulators based on eigenvector continuation27,28,29 that accurately mimic the outputs of the ab initio methods but at several orders of magnitude lower computational cost. We consider the following history-matching observables: nucleon–nucleon scattering phase shifts up to an energy of 200 MeV; the energy, radius and quadrupole moment of 2H; and the energies and radii of 3H, 4He and 16O. We perform five waves of this global parameter search (Extended Data Figs. 1 and 2), sequentially ruling out implausible LECs that yield model predictions too far from experimental data. For this purpose, we use an implausibility measure (Methods) that links our model predictions and experimental observations as

$$z=M(\theta )+{\varepsilon }_{\exp }+{\varepsilon }_{{{{\rm{em}}}}}+{\varepsilon }_{{{{\rm{method}}}}}+{\varepsilon }_{{{{\rm{model}}}}},$$
(1)

relating the experimental observations z to emulated ab initio predictions M(θ) via the random variables \({\varepsilon }_{\exp }\), εem, εmethod and εmodel that represent experimental uncertainties, the emulator precision, method approximation errors and the model discrepancy due to the EFT truncation at next-to-next-to leading order, respectively. The parameter vector θ corresponds to the 17 LECs at this order. The method error represents, for example, model space truncations and other approximations in the employed ab initio many-body solvers. The model discrepancy εmodel can be specified probabilistically since we assume to operate with an order-by-order improvable EFT description of the nuclear interaction (see Methods for details).

The final result of the five history-matching waves is a set of 34 non-implausible samples in the 17-dimensional parameter space of the LECs. We then perform ab initio calculations for nuclear observables in 48Ca and 208Pb, as well as for properties of infinite nuclear matter.

Ab initio computations of 208Pb

We employ the coupled-cluster (CC)12,30,31, in-medium similarity renormalization group (IMSRG)32 and many-body perturbation theory (MBPT) methods to approximately solve the Schrödinger equation and obtain the ground-state energy and nucleon densities of 48Ca and 208Pb. We analyse the model space convergence and use the differences between the CC, IMSRG and MBPT results to estimate the method approximation errors (Methods and Extended Data Figs. 3 and 4). The computational cost of these methods scales (only) polynomially with increasing numbers of nucleons and single-particle orbitals. The main challenge in computing 208Pb is the vast number of matrix elements of the three-nucleon (3N) force which must be handled. We overcome this limitation by using a recently introduced storage scheme in which we only store linear combinations of matrix elements directly entering the normal-ordered two-body approximation19 (see Methods for details).

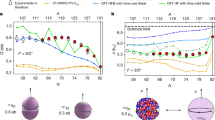
Our ab initio predictions for finite nuclei are summarized in Fig. 2. The statistical approach that leads to these results is composed of three stages. First, history matching identified a set of 34 non-implausible interaction parameterizations. Second, model calibration is performed by weighting these parameterizations—serving as prior samples—using a likelihood measure according to the principles of sampling/importance resampling33. This yields 34 weighted samples from the LEC posterior probability density function (Extended Data Fig. 5). Specifically, we assume independent EFT and many-body method errors and construct a normally distributed data likelihood encompassing the ground-state energy per nucleon E/A and the point-proton radius Rp for 48Ca, and the energy \({E}_{{2}^{+}}\) of its first excited 2+ state. Our final predictions are therefore conditional on this calibration data.

Fig. 2: Ab initio posterior predictive distributions for light to heavy nuclei.
figure 2

Model checking is indicated by green (blue) distributions, corresponding to observables used for history-matching (likelihood calibration), while pure predictions are shown as pink distributions. The nuclear observables shown are the quadrupole moment Q, point-proton radii Rp, ground-state energies E (or energy per nucleon E/A), 2+ excitation energy \({E}_{{2}^{+}}\) and electric dipole polarizabilities αD. See Extended Data Table 1 for the numerical specification of the experimental data (z), errors (σi), medians (white circle) and 68% credibility regions (thick bar). The prediction for Rskin(208Pb) in the bottom panel is shown on an absolute scale and compared with experimental results using electroweak5 (purple), hadronic34,35 (red), electromagnetic4 (green) and gravitational wave36 (blue) probes (from top to bottom; see Extended Data Fig. 7b for details).

Source data

Full size image

We have tested the sensitivity of final results to the likelihood definition by repeating the calibration with a non-diagonal covariance matrix or a Student t distribution with heavier tails, finding small (~1%) differences in the predicted credible regions. The EFT truncation errors are quantified by studying ab initio predictions at different orders in the power counting for 48Ca and infinite nuclear matter. We validate our ab initio model and error assignments by computing the posterior predictive distributions, including all relevant sources of uncertainty, for both the replicated calibration data (blue) and the history-matching observables (green) (Fig. 2). The percentage ratios σtot/z of the (theory-dominated) total uncertainty to the experimental value are given in the right margin.

Finally, having built confidence in our ab initio model and underlying assumptions, we predict Rskin(208Pb), E/A and Rp for 208Pb, αD for 48Ca and 208Pb as well as nuclear matter properties, by employing importance resampling33. The corresponding posterior predictive distributions for 48Ca and 208Pb observables are shown in Fig. 2 (lower panels, pink). Our prediction Rskin(208Pb) = 0.14–0.20 fm exhibits a mild tension with the value extracted from the recent parity-violating electron scattering experiment PREX5 but is consistent with the skin thickness extracted from elastic proton scattering34, antiprotonic atoms35 and coherent pion photoproduction4 as well as constraints from gravitational waves from merging neutron stars36.

We also compute the weak form factor Fw(Q2) at momentum transfer QPREX = 0.3978(16) fm−1, which is more directly related to the parity-violating asymmetry measured in the PREX experiment. We observe a strong correlation with the more precisely measured electric charge form factor Fch(Q2) (Fig. 3b). While we have not quantified the EFT and method errors for these observables, we find a small variance among the 34 non-implausible predictions for the difference Fw(Q2) − Fch(Q2) for both 48Ca and 208Pb (Fig. 3c).

Fig. 3: Posterior predictive distribution for Rskin(208Pb) and nuclear matter at saturation density.
figure 3

a, Predictions for the saturation energy per particle E0/A and density ρ0 of symmetric nuclear matter, its compressibility K, the symmetry energy S and its slope L are correlated with the those for Rskin(208Pb). The sampled bivariate distributions (pink/orange squares) are shown with 68% and 90% credible regions (black lines) and a scatter plot of the predictions with the 34 non-implausible samples before error sampling (blue dots). Empirical nuclear-matter properties are indicated by purple bands (Extended Data Table 2). b, Predictions with the 34 non-implausible samples for the electric Fch versus weak Fw charge form factors for 208Pb at the momentum transfer considered in the PREX experiment5. c, The difference between the electric and weak charge form factors for 48Ca and 208Pb at the momentum transfers QCREX = 0.873 fm−1 and QPREX = 0.3978 fm−1 that are relevant for the CREX and PREX experiments, respectively. Experimental data (purple bands) in b and c are from ref. 5, the size of the markers indicates the importance weight and blue lines correspond to weighted means.

Source data

Full size image

Ab initio computations of infinite nuclear matter

We also make predictions for nuclear-matter properties by employing the CC method on a momentum space lattice37 with a Bayesian machine-learning error model to quantify the uncertainties from the EFT truncation14 and the CC method (see Methods and Extended Data Fig. 6 for details). The observables we compute are the saturation density ρ0, the energy per nucleon of symmetric nuclear matter E0/A, its compressibility K, the symmetry energy S (that is, the difference between the energy per nucleon of neutron matter and symmetric nuclear matter), and its slope L. The posterior predictive distributions for these observables are shown in Fig. 3a. These distributions include samples from the relevant method and model error terms. Overall, we reveal relevant correlations among observables, previously indicated in mean-field models, and find good agreement with empirical bounds38. The last row shows the resulting correlations with Rskin(208Pb) in our ab initio framework. In particular, we find essentially the same correlation between Rskin(208Pb) and L as observed in mean-field models (Extended Data Fig. 7b).

Discussion

The predicted range of the 208Pb neutron skin thickness (Extended Data Table 2) is consistent with several extractions4,39,40, each of which involves some model dependence, and in mild tension (approximately 1.5σ) with the recent PREX result5. Ab initio computations yield a thin skin and a narrow range because the isovector physics is constrained by scattering data8,13,41. A thin skin was also predicted in 48Ca (ref. 15). We find that both Rskin(208Pb) = 0.14–0.20 fm and the slope parameter L = 38–69 MeV are strongly correlated with scattering in the 1S0 partial wave for laboratory energies around 50 MeV (the strongest two-neutron channel allowed by the Pauli principle, with the energy naively corresponding to the Fermi energy of neutron matter at 0.8ρ0) (Extended Data Fig. 7a). It is possible, analogous to findings in mean-field theory1,42, to increase L beyond the range predicted in this work by tuning a contact in the 1S0 partial wave and simultaneously readjusting the three-body contact to maintain realistic nuclear saturation. However, this large slope L and increased Rskin come at the cost of degraded 1S0 scattering phase shifts, well beyond the corrections expected from higher-order terms (Extended Data Fig. 8). The large range of L and Rskin obtained in mean-field theory is a consequence of scattering data not being incorporated. It will be important to confront our predictions with more precise experimental measurements43,44. If the tension between scattering data and neutron skins persists, it will represent a serious challenge to our ab initio description of nuclear physics.

Our work demonstrates that ab initio approaches using nuclear forces from chiral EFT can consistently describe data from nucleon–nucleon scattering, few-body systems and heavy nuclei within the estimated theoretical uncertainties. Information contained in nucleon–nucleon scattering significantly constrains the properties of neutron matter. This same information constrains neutron skins, which provide a non-trivial empirical check on the reliability of ab initio predictions for the neutron-matter equation of state. Moving forward, it will be important to extend these calculations to higher orders in the EFT, both to further validate the error model and to improve precision, and to push the cut-off to higher values to confirm regulator independence. The framework presented herein will enable predictions with quantified uncertainties across the nuclear chart, advancing towards the goal of a single unified framework for describing low-energy nuclear physics.

Methods

Hamiltonian and model space

The many-body approaches used in this work, viz. CC, IMSRG, and many-body perturbation theory (MBPT), start from the intrinsic Hamiltonian

$$H={T}_{{{{\rm{kin}}}}}-{T}_{{{{\rm{CoM}}}}}+{V}_{{{{\rm{NN}}}}}+{V}_{{{{\rm{3N}}}}},$$
(2)

where Tkin is the kinetic energy, TCoM is the kinetic energy of the centre of mass, VNN is the nucleon–nucleon interaction and V3N is the 3N interaction. To facilitate the convergence of heavy nuclei, the interactions employed in this work used a non-local regulator with a cut-off Λ = 394 MeV c−1. Specifically, the VNN regulator is \(f(p)=\exp {({p}^{2}/{{{\varLambda }}}^{2})}^{n}\) and the V3N regulator is \(f(p,q)=\exp {[-({p}^{2}+3{q}^{2}/4)/{{{\varLambda }}}^{2}]}^{n}\) with n = 4. Results should be independent of this choice, up to higher-order corrections, provided renormalization group invariance of the EFT. However, increasing the momentum scale of the cut-off leads to harder interactions, considerably increasing the required computational effort. We represent the 34 non-implausible interactions that resulted from the history-matching analysis in the Hartree–Fock basis in a model space of up to 15 major harmonic oscillator shells (\(e=2n+l\le {e}_{\max }=14\), where n and l denote the radial and orbital angular momentum quantum numbers, respectively) with oscillator frequency ℏω = 10 MeV. Due to storage limitations, the 3N force had an additional energy cut given by \({e}_{1}+{e}_{2}+{e}_{3}\le {E}_{3\max }=28\). After obtaining the Hartree–Fock basis for each of the 34 non-implausible interactions, we capture 3N force effects via the normal-ordered two-body approximation before proceeding with the CC, IMSRG and MBPT calculations46,47. The convergence behaviour in \({e}_{\max }\) and \({E}_{{{{\rm{3max}}}}}\) is illustrated in Extended Data Fig. 3, where we use an interaction with a high likelihood that generates a large correlation energy. Thus, its convergence behaviour represents the worst case among the 34 non-implausible interactions. The model space converged results are investigated with \({E}_{{{{\rm{3max}}}}}\to 3{e}_{\max }\) and \({e}_{\max }\to \infty\) extrapolations. The functions \({E}_{{{{\rm{gs}}}}}\approx {c}_{0}{e}^{-{[({E}_{{{{\rm{3max}}}}}-{c}_{1})/{c}_{2}]}^{2}}+{E}_{{{{\rm{gs}}}}}({E}_{{{{\rm{3max}}}}}=\infty )\) and \({E}_{{{{\rm{gs}}}}}\approx {d}_{0}{e}^{-{d}_{1}{L}_{{{{\rm{IR}}}}}}+{E}_{{{{\rm{gs}}}}}({e}_{\max }=\infty )\) with \({L}_{{{{\rm{IR}}}}}=\sqrt{2({e}_{\max }+7/2)b}\) (where b is the harmonic oscillator length and the ci and di are the fitting parameters) are used as the asymptotic forms for \({E}_{{{{\rm{3max}}}}}\) (ref. 19) and \({e}_{\max }\) 48,49), respectively. Through the extrapolations, the ground-state energies computed with \({e}_{\max }=14\) and \({E}_{{{{\rm{3max}}}}}=28\) are shifted by −75 ± 60 MeV. Likewise, the extrapolations of proton and neutron radii with the functional form given in refs. 19,48,49 yield a small (+0.005 ± 0.010 fm) shift of the neutron skin thickness.

IMSRG calculations

The IMSRG calculations32,50 were performed at the IMSRG(2) level, using the Magnus formulation51. Operators for the point-proton and point-neutron radii, form factors and the electric dipole operator were consistently transformed. The dipole polarizablility αD was computed using the equations-of-motion (EOM) method truncated at the two-particle-two-hole level (that is, the EOM-IMSRG(2,2) approximation52) and the Lanczos continued fraction method53. We compute the weak and charge form factors using the parameterization presented in ref. 54, though the form given in ref. 55 yields nearly identical results.

MBPT calculations

MBPT theory calculations for 208Pb were performed in the Hartree–Fock basis to third order for the energies and to second order for radii.

CC calculations

The CC calculations of 208Pb were truncated at the singles-and-doubles excitation level, known as the CCSD approximation12,30,31. We estimated the contribution from triples excitations to the ground-state energy of 208Pb as 10% of the CCSD correlation energy (which is a reliable estimate for closed-shell systems31).

Extended Data Fig. 4 compares the different many-body approaches used in this work (that is CC, IMSRG and MBPT) and allows us to estimate the uncertainties related to our many-body approach in computing the ground-state observables for 208Pb. The point proton and neutron radii are computed as ground-state expectation values (see, for example, ref. 15 for details). For 48Ca, we used a Hartree–Fock basis consisting of 15 major oscillator shells with an oscillator spacing of ℏω = 16 MeV, while for 3N forces we used \({E}_{{{{\rm{3max}}}}}=16\), which is sufficiently large to obtain converged results in this mass region. Here, we computed the ground-state energy using the Λ-CCSD(T) approximation56, which include perturbative triples corrections. The 2+ excited state in 48Ca was computed using the EOM CCSD approach57, and we estimated a −1 MeV shift from triples excitations based on EOM-CCSD(T) calculations of 48Ca and 78Ni using similar interactions58.

For the history-matching analysis, we used an emulator for the 16O ground-state energy and charge radius that was constructed using the recently developed sub-space projected (SP) CC method29. For higher precision in the emulator, we went beyond the SP-CCSD approximation used in ref. 29 and included leading-order triples excitations via the CCSDT-3 method59. The CCSDT-3 ground-state training vectors for 16O were obtained starting from the Hartree–Fock basis of the recently developed chiral interaction ΔNNLOGO(394) of ref. 60 in a model space consisting of 11 major harmonic oscillator shells with oscillator frequency ℏω = 16 MeV and \({E}_{{{{\rm{3max}}}}}=14\). The emulator used in the history matching was constructed by selecting 68 different training points in the 17-dimensional space of LECs using a space-filling Latin hypercube design with a 10% variation around the ΔNNLOGO(394) LECs. At each training point, we then performed a CCSDT-3 calculation to obtain the training vectors, for which we then construct the sub-space projected norm and Hamiltonian matrices. Once the SP-CCSDT-3 matrices are constructed, we may obtain the ground-state energy and charge radii for any target values of the LECs by diagonalizing a 68 × 68 generalized eigenvalue problem (see ref. 29 for more details). We checked the accuracy of the emulator by cross-validation against full-space CCSDT-3 calculations as demonstrated in Extended Data Fig. 4a and found a relative error that was smaller than 0.2%.

The nuclear-matter equation of state and saturation properties are computed with the CCD(T) approximation which includes doubles excitations and perturbative triples corrections. The 3N forces are considered beyond the normal-ordered two-body approximation by including the residual 3N force contribution in the triples. The calculations are performed on a cubic lattice in momentum space with periodic boundary conditions. The model space is constructed with \({(2{n}_{\max }+1)}^{3}\) momentum points, and we use \({n}_{\max }=4(3)\) for pure neutron matter (symmetric nuclear matter) and obtain converged results. We perform calculations for systems of 66 neutrons (132 nucleons) for pure neutron matter (symmetric nuclear matter) since results obtained with those particle numbers exhibit small finite-size effects37.

Iterative history matching

In this work, we use an iterative approach known as history matching25,26 in which the model, solved at different fidelities, is confronted with experimental data z using equation (1). Obviously, we do not know the exact values of the errors in equation (1), hence we represent them as random variables and specify reasonable forms for their statistical distributions, in alignment with the Bayesian paradigm.

For many-body systems, we employ quantified method and (A = 16) emulator errors, as discussed above and summarized in Extended Data Table 1. For A ≤ 4 nuclei, we use the no-core shell model in Jacobi coordinates61 and eigenvector continuation emulators28. The associated method and emulator errors are very small. Probabilistic attributes of the model discrepancy terms are assigned based on the expected EFT convergence pattern62,63. For the history-matching observables considered here, we use point estimates of model errors from ref. 64.

The aim of history matching is to estimate the set \({{{\mathcal{Q}}}}(z)\) of parameterizations θ for which the evaluation of a model M(θ) yields an acceptable (or at least not implausible) match to a set of observations z. History matching has been employed in various studies involving complex computer models65,66,67,68 ranging, for example, from the effects of climate modelling69,70 to systems biology71.

We introduce the individual implausibility measure

$${I}_{i}^{2}(\theta )=\frac{| {M}_{i}(\theta )-{z}_{i}{| }^{2}}{{{{\rm{Var}}}}\left({M}_{i}(\theta )-{z}_{i}\right)},$$
(3)

which is a function over the input parameter space and quantifies the (mis-)match between our (emulated) model output Mi(θ) and the observation zi for an observable in the target set \({{{\mathcal{Z}}}}\). We mainly employ a maximum implausibility measure as the restricting quantity. Specifically, we consider a particular value for θ as implausible if

$${I}_{M}(\theta )\equiv \mathop{\max }\limits_{{z}_{i}\in {{{\mathcal{Z}}}}}{I}_{i}(\theta ) > {c}_{I},$$
(4)

with cI ≡ 3.0, appealing to Pukelheim’s three-sigma rule72. In accordance with the assumptions leading to equation (1), the variance in the denominator of equation (3) is a sum of independent squared errors. Generalizations of these assumptions are straightforward if additional information on error covariances or possible inaccuracies in our error model would become available.

An important strength of the history matching is that we can proceed iteratively, excluding regions of input space by imposing cut-offs on implausibility measures that can include additional observables zi and corresponding model outputs Mi with possibly refined emulators as the parameter volume is reduced. The history-matching process is designed to be independent of the order in which observables are included, as is discussed in ref. 67. This is an important feature because it allows for efficient choices regarding such orderings. The iterative history matching proceeds in waves according to a straightforward strategy that can be summarized as follows:

  1. 1.

    At wave j: Evaluate a set of model runs over the current non-implausible (NI) volume \({{{{\mathcal{Q}}}}}_{j}\) using a space-filling design of sample values for the parameter inputs θ. Choose a rejection strategy based on implausibility measures for a set \({{{{\mathcal{Z}}}}}_{j}\) of informative observables.

  2. 2.

    Construct or refine emulators for the model predictions across \({{{{\mathcal{Q}}}}}_{j}\).

  3. 3.

    The implausibility measures are then calculated over \({{{{\mathcal{Q}}}}}_{j}\) using the emulators, and implausibility cut-offs are imposed. This defines a new, smaller non-implausible volume \({{{{\mathcal{Q}}}}}_{j+1}\) which should satisfy \({\mathcal{Q}}_{j+1}\subset {\mathcal{Q}}_{j}\).

  4. 4.

    Unless (a) computational resources are exhausted or (b) all considered points in the parameter space are deemed implausible, we may include additional informative observables in the considered set \({{{{\mathcal{Z}}}}}_{j+1}\), and return to step 1.

  5. 5.

    If step 4(a) is true, we generate a number of acceptable runs from the final non-implausible volume \({{{{\mathcal{Q}}}}}_{{{{\rm{final}}}}}\), sampled according to scientific need.

The ab initio model for the observables we consider includes at most 17 parameters: 4 subleading pion–nucleon couplings, 11 nucleon–nucleon contact couplings and two short-ranged 3N couplings. To identify a set of non-implausible parameter samples, we performed iterative history matching in four waves using observables and implausibility measures, as summarized in Extended Data Fig. 1b. For each wave, we employ a sufficiently dense Latin hypercube set of several million candidate parameter samples. For the model evaluations, we utilized fast computations of neutron–proton scattering phase shifts and efficient emulators for the few- and many-body history-matching observables. See Extended Data Table 1 and Extended Data Fig. 2 for the list of history-matching observables and information on the errors that enter the implausibility measure in equation (3). The input volume for wave 1 incorporates the naturalness expectation for LECs, but still includes large ranges for the relevant parameters as indicated by the panel ranges in Extended Data Fig. 1a. In all four waves, the input volume for c1,2,3,4 is a four-dimensional hypercube mapped onto the multivariate Gaussian probability density function (PDF) resulting from a Roy–Steiner analysis of pion–nucleon scattering data73. In wave 1 and wave 2, we sampled all relevant parameter directions for the set of included two-nucleon observables. In wave 3, the 3H and 4He observables were added such that the 3N force parameters cD and cE can also be constrained. Since these observables are known to be rather insensitive to the four model parameters acting solely in P waves, we ignored this subset of the inputs and compensated by slightly enlarging the corresponding method errors. This is a well-known emulation procedure called inactive parameter identification25. For wave 4, we considered all 17 model parameters and added the ground-state energy and radius of 16O to the set \({{{{\mathcal{Z}}}}}_{4}\) and emulated the model outputs for 5 × 108 parameter samples. By including oxygen data, we explore the modelling capabilities of our ab initio approach. Extended Data Fig. 1a summarizes the sequential non-implausible volume reduction, wave-by-wave, and indicates the set of 4,337 non-implausible samples after the fourth wave. Note that the use of history matching would, in principle, allow a detailed study of the information content of various observables in heavy-mass nuclei. Such an analysis, however, requires an extensive set of reliable emulators and lies beyond the scope of the present work. The volume reduction is determined by the maximum implausibility cut-off in equation (4) with additional confirmation from the optical depths (which indicate the density of non-implausible samples; see equations (25) and (26) in ref. 71). The non-implausible samples summarize the parameter region of interest and can directly provide insight regarding the interdependences between parameters induced by the match to observed data. This region is also where we would expect the posterior distribution to reside, and we note that our history-matching procedure has allowed us to reduce its size by more than seven orders of magnitude compared with the prior volume (Extended Data Fig. 1b).

As a final step, we confront the set of non-implausible samples from wave 4 with neutron–proton scattering phase shifts such that our final set of non-implausible samples has been matched with all history-matching observables. For this final implausibility check, we employ a slightly less strict cut-off and allow the first, second and third maxima of Ii(θ) (for \({z}_{i}\in {{{{\mathcal{Z}}}}}_{{{{\rm{final}}}}}\)) to be 5.0, 4.0 and 3.0, respectively, accommodating the more extreme maxima we may anticipate when considering a significantly larger number of observables. The end result is a set of 34 non-implausible samples that we use for predicting 48Ca and 208Pb observables, as well as the equation of state of both symmetric nuclear matter and pure neutron matter.

Posterior predictive distributions

The 34 non-implausible samples from the final history-matching wave are used to compute energies, radii of proton and neutron distributions and electric dipole polarizabilities (αD) for 48Ca and 208Pb. They are also used to compute the electric and weak charge form factors for the same nuclei at a relevant momentum transfer, and the energy per particle of infinite nuclear matter at various densities to extract key properties of the nuclear equation of state (see below). These results are shown in Fig. 3(blue circles).

To make quantitative predictions, with a statistical interpretation, for Rskin(208Pb) and other observables, we use the same 34 parameter sets to extract representative samples from the posterior PDF \(p(\theta | {{{{\mathcal{D}}}}}_{{{{\rm{cal}}}}})\). Bulk properties (energies and charge radii) of 48Ca together with the structure-sensitive 2+ excited-state energy of 48Ca are used to define the calibration data set \({{{{\mathcal{D}}}}}_{{{{\rm{cal}}}}}\). The IMSRG and CC convergence studies make it possible to quantify the method errors. These are summarized in Extended Data Table 1. The EFT truncation errors are quantified by adopting the EFT convergence model74,75 for observable y

$$y={y}_{{{{\rm{ref}}}}}\left(\mathop{\sum }\limits_{i=0}^{k}{c}_{i}{Q}^{i}+\mathop{\sum }\limits_{i=k+1}^{\infty }{c}_{i}{Q}^{i}\right),$$
(5)

with observable coefficients ci that are expected to be of natural size, and the expansion parameter Q = 0.42 following our Bayesian error model for nuclear matter at the relevant density (see below). The first sum in the parenthesis is the model prediction yk(θ) of observable y at truncation order k in the chiral expansion. The second sum than represents the model error because it includes the terms that are not explicitly included. We can quantify the magnitude of these terms by learning about the distribution for ci, which we assume to be described by a single normal distribution per observable type with zero mean and a variance parameter \({\bar{c}}^{2}\). We employ the nuclear-matter error analysis for the energy per particle of symmetric nuclear matter (described below) to provide the model error for E/A in 48Ca and 208Pb. For radii and electric dipole polarizabilities, we employ the next-to leading order and next-to-next-to leading order interactions of ref. 60 and compute these observables at both orders for various Ca, Ni and Sn isotopes. The reference values yref are set to r0 A1/3 for radii (with r0 = 1.2 fm) and to the experimental value for αD. From these data, we extract \({\bar{c}}^{2}\) and perform the geometric sum of the second term in equation (5). The resulting standard deviations for model errors are summarized in Extended Data Table 1.

At this stage, we can approximately extract samples from the parameter posterior \(p(\theta | {{{{\mathcal{D}}}}}_{{{{\rm{cal}}}}})\) by employing the established method of sampling/importance resampling33,76. We assume a uniform prior probability for the non-implausible samples, and we introduce a normally distributed likelihood \({{{\mathcal{L}}}}({{{{\mathcal{D}}}}}_{{{{\rm{cal}}}}}| \theta )\), assuming independent experimental, method and model errors. The prior for c1,2,3,4 is the multivariate Gaussian resulting from a Roy–Steiner analysis of pion–nucleon scattering data73. Defining importance weights

$${q}_{i}={{{\mathcal{L}}}}({{{{\mathcal{D}}}}}_{{{{\rm{cal}}}}}| {\theta }_{i})/\mathop{\sum }\limits_{j=1}^{n}{{{\mathcal{L}}}}({{{{\mathcal{D}}}}}_{{{{\rm{cal}}}}}| {\theta }_{j}),$$
(6)

we draw samples θ* from the discrete distribution {θ1, …, θn} with probability mass qi on θi. These samples are then approximately distributed according to the parameter posterior that we are seeking33,76.

Although we are operating with a finite number of n = 34 representative samples from the parameter PDF, it is reassuring that about half of them are within a factor of two from the most probable one in terms of the importance weight (Extended Data Fig. 5). Consequently, our final predictions will not be dominated by a very small number of interactions. In addition, as we do not anticipate the parameter PDF to be of a particularly complex shape, based on the results of the history match, consideration of the various error structures in the analysis and on the posterior predictive distributions (PPDs) shown in Fig. 3, and as we are mainly interested in examining such lower one- or two-dimensional PPDs, this sample size was deemed sufficient and the corresponding sampling error assumed subdominant. We use these samples to draw corresponding samples from

$${{{{\rm{PPD}}}}}_{{{{\rm{parametric}}}}}=\{{y}_{k}(\theta ):\theta \sim p(\theta | {{{{\mathcal{D}}}}}_{{{{\rm{cal}}}}})\}.$$
(7)

This PPD is the set of all model predictions computed over likely values of the parameters, that is, drawing from the posterior PDF for θ. The full PPD is then defined, in analogy with equation (7), as the set evaluation of y which is the sum

$$y={y}_{k}+{\epsilon }_{{{{\rm{method}}}}}+{\epsilon }_{{{{\rm{model}}}}},$$
(8)

where we assume method and model errors to be independent of the parameters. In practice, we produce 104 samples from this full PPD for y by resampling the 34 samples of the model PPD in equation (7) according to their importance weights, and adding samples from the error terms in equation (8). We perform model checking by comparing this final PPD with the data used in the iterative history-matching step, and in the likelihood calibration. In addition, we find that our predictions for the measured electric dipole polarizabilities of 48Ca and 208Pb as well as bulk properties of 208Pb serve as a validation of the reliability of our analysis and assigned errors (Fig. 2 and Extended Data Table 1).

In addition, we explored the sensitivity of our results to modifications of the likelihood definition. Specifically, we used a Student t distribution (ν = 5) to see the effects of allowing heavier tails, and we introduced an error covariance matrix to study the effect of possible correlations (with ρ ≈ 0.7) between the errors in the binding energy and radius of 48Ca. In the end, the differences in the extracted credibility regions was ~1%, and we therefore present only results obtained with the uncorrelated, multivariate normal distribution.

Our final predictions for Rskin(208Pb), Rskin(48Ca) and nuclear-matter properties are presented in Fig. 3 and Extended Data Table 2. For these observables, we use the Bayesian machine learning error model described below to assign relevant correlations between equation-of-state observables. For the model errors in Rskin(208Pb) and L, we use a correlation coefficient of ρ = 0.9 as motivated by the strong correlation between the observables computed with the 34 non-implausible samples. Note that S, L and K are computed at the specific saturation density of the corresponding non-implausible interaction.

Bayesian machine learning error model

Similar to equation (1), the predicted nuclear matter observables can be written as

$$y={y}_{k}(\rho )+{\varepsilon }_{k}(\rho )+{\varepsilon }_{{{{\rm{method}}}}}(\rho ),$$
(9)

where yk(ρ) is the CC prediction using our EFT model truncated at order k, εk(ρ) is the EFT truncation (model) error and εmethod(ρ) is the CC method error. In this work, we apply a Bayesian machine learning error model14 to quantify the density dependence of both the method and truncation errors. The error model is based on multi-task Gaussian processes that learn both the size and the correlations of the target errors from given prior information. Following a physically motivated Gaussian process (GP) model14, the EFT truncation errors εk at given density ρ are distributed as

$${\varepsilon }_{k}(\rho )\,| \,{\bar{c}}^{2},l,Q \sim {{{\rm{GP}}}}[0,{\bar{c}}^{2}{R}_{{\varepsilon }_{k}}(\rho ,\rho ^{\prime} ;l)],$$
(10)

with

$${R}_{{\varepsilon }_{k}}(\rho ,\rho ^{\prime} ;l)={y}_{{{{\rm{ref}}}}}(\rho ){y}_{{{{\rm{ref}}}}}(\rho ^{\prime} )\frac{{[Q(\rho )Q(\rho ^{\prime} )]}^{k+1}}{1-Q(\rho )Q(\rho ^{\prime} )}r(\rho ,\rho ^{\prime} ;l).$$
(11)

Here, k = 3 for the ΔNNLO(394) EFT model used in this work, while \({\bar{c}}^{2}\), l and Q are hyperparameters corresponding to the variance, the correlation length and the expansion parameter. Finally, we choose the reference scale yref to be the EFT leading-order prediction. The mean of the Gaussian process is set to be zero since the order-by-order truncation error can be either positive or negative and the correlation function \(r(\rho ,\rho ^{\prime} ;l)\) in equation (11) is the Gaussian radial basis function.

We employ Bayesian inference to optimize the Gaussian process hyperparameters using order-by-order predictions of the equation of state for both pure neutron matter and symmetric nuclear matter with the Δ-full interactions from ref. 64. In this work, we find \({\bar{c}}_{{{{\rm{PNM}}}}}=0.99\) and lPNM = 88 fm−1 for pure neutron matter and \({\bar{c}}_{{{{\rm{SNM}}}}}=1.66\) and lSNM = 0.45 fm−1 for symmetric nuclear matter. This leads to Q = 0.41 when estimating the model errors for E / A in 48Ca and 208Pb.

The above Gaussian processes only describe the correlated structure of truncation errors for one type of nucleonic matter. In addition, the correlation between pure neutron matter and symmetric nuclear matter is crucial for correctly assigning errors to observables that involve both E/N and E/A (such as the symmetry energy S). For this purpose, we use a multitask Gaussian process that simultaneously describes the truncation errors of pure neutron matter and symmetric nuclear matter according to

$$\left[\begin{array}{c}{\varepsilon }_{k,{{{\rm{PNM}}}}}\\ {\varepsilon }_{k,{{{\rm{SNM}}}}}\end{array}\right] \sim {{{\rm{GP}}}}\left(\left[\begin{array}{c}0\\ 0\end{array}\right],\left[\begin{array}{cc}{K}_{11}&{K}_{12}\\ {K}_{21}&{K}_{22}\end{array}\right]\right),$$
(12)

where K11 and K22 are the covariance matrices generated from the kernel function \({\bar{c}}^{2}{R}_{{\varepsilon }_{k}}(\rho ,\rho ^{\prime} ;l)\) for pure neutron matter and symmetric nuclear matter, respectively, while K12 (K21) is the cross-covariance as in ref. 77.

Regarding the CC method error, different sources of uncertainty should be considered. The truncation error of the cluster operator (εcc) and the finite-size effect (εfs) are the main ones, and the total method error is then εmethod = εcc + εfs. Following the Bayesian error model, we have the following general expression for the method error:

$${\varepsilon }_{{{{\rm{me}}}}}(\rho )\,| \,{\bar{c}}_{{{{\rm{me}}}}}^{2},{l}_{{{{\rm{me}}}}}, \sim {{{\rm{GP}}}}[0,{\bar{c}}_{{{{\rm{me}}}}}^{2}{R}_{{{{\rm{me}}}}}(\rho ,\rho ^{\prime} ;{l}_{{{{\rm{me}}}}})],$$
(13)

with

$${R}_{{{{\rm{me}}}}}(\rho ,\rho ^{\prime} ;{l}_{{{{\rm{me}}}}})={y}_{{{{\rm{me,ref}}}}}(\rho ){y}_{{{{\rm{me,ref}}}}}(\rho ^{\prime} )r(\rho ,\rho ^{\prime} ;{l}_{{{{\rm{me}}}}}).$$
(14)

Here, the subscript ‘me’ stands for either the cluster operator truncation ‘cc’ or the finite-size effect ‘fs’ method error. For the cluster operator truncation errors εcc, the reference scale yme,ref is taken to be the CCD(T) correlation energy. The Gaussian processes are then optimized with data from different interactions by assuming that the energy difference between CCD and CCD(T) can be used as an approximation of the cluster operator truncation error. The correlation lengths learned from the training data are lme,PNM = 0.83 fm−1 for pure neutron matter and lme,SNM = 0.39 fm−1 for symmetric nuclear matter. Based on the convergence study, we take ±10% of the correlation energy as the 95% credible interval, which gives \({\bar{c}}_{{{{\rm{me}}}}}=0.05\) for εcc. For the finite-size effect εfs, the reference scale is taken to be the CCD(T) ground-state energy. Then, following ref. 37, we use ±0.5% (±4%) of the ground-state energy of the pure neutron matter (the symmetric nuclear matter) as a conservative estimation of the finite-size effect (95% credible interval) when using periodic boundary conditions with 66 neutrons (132 nucleons) around the saturation point. This leads to \({\bar{c}}_{{{{\rm{me}}}},PNM}=0.0025\) and \({\bar{c}}_{{{{\rm{me}}}},SNM}=0.02\) for εfs. The finite-size effects of different densities are clearly correlated, while there are insufficient data to learn its correlation structure. Here, we simply used 0.83 fm−1 (0.39 fm−1) as the correlation length for pure neutron matter (symmetric nuclear matter) and assume zero correlation between pure neutron matter and symmetric nuclear matter.

Once the model and method errors are determined, it is straightforward to sample these errors from the corresponding covariance matrix and produce the equation-of-state predictions using equation (9) for any given interaction. This sampling procedure is crucial for generating the posterior predictive distribution of nuclear-matter observables shown in Fig. 3a. The CCD(T) calculations for the nuclear-matter equation of state and the corresponding 2σ credible interval for the method and model errors are illustrated in Extended Data Fig. 6. The sampling procedure is made explicit with three randomly sampled equation-of-state predictions. Note that, even though the sampled errors for one given density appear to be random, the multi-task Gaussian processes will guarantee that the sampled equations of state of nuclear matter are smooth and properly correlated with each other.