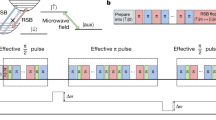
Abstract
Mesoscopic superpositions of distinguishable coherent states provide an analogue of the ‘Schrödinger’s cat’ thought experiment1,2. For mechanical oscillators these have primarily been realized using coherent wavepackets, for which the distinguishability arises as a result of the spatial separation of the superposed states3,4,5. Here we demonstrate superpositions composed of squeezed wavepackets, which we generate by applying an internal-state-dependent force to a single trapped ion initialized in a squeezed vacuum state with nine decibel reduction in the quadrature variance. This allows us to characterize the initial squeezed wavepacket by monitoring the onset of spin–motion entanglement, and to verify the evolution of the number states of the oscillator as a function of the duration of the force. In both cases we observe clear differences between displacements aligned with the squeezed and anti-squeezed axes. We observe coherent revivals when inverting the state-dependent force after separating the wavepackets by more than 19 times the ground-state root mean squared extent, which corresponds to 56 times the root mean squared extent of the squeezed wavepacket along the displacement direction. Aside from their fundamental nature, these states may be useful for quantum metrology6 or quantum information processing with continuous variables7,8,9.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Wineland, D. J. Nobel lecture. Superposition, entanglement, and raising Schrödinger’s cat. Rev. Mod. Phys. 85, 1103–1114 (2013).
Haroche, S. Nobel lecture. Controlling photons in a box and exploring the quantum to classical boundary. Rev. Mod. Phys. 85, 1083–1102 (2013).
Monroe, C., Meekhof, D. M., King, B. E. & Wineland, D. J. A ‘Schrödinger cat’ superposition state of an atom. Science 272, 1131–1136 (1996).
McDonnell, M. J. et al. Long-lived mesoscopic entanglement outside the Lamb–Dicke regime. Phys. Rev. Lett. 98, 063603 (2007).
Haljan, P. C., Brickman, K.-A., Deslauriers, L., Lee, P. J. & Monroe, C. Spin-dependent forces on trapped ions for phase-stable quantum gates and motional Schrödinger cat states. Phys. Rev. Lett. 94, 153602 (2005).
Munro, W. J., Nemoto, K., Milburn, G. J. & Braunstein, S. L. Weak-force detection with superposed coherent states. Phys. Rev. A 66, 023819 (2002).
Weedbrook, C. et al. Gaussian quantum information. Rev. Mod. Phys. 84, 621–669 (2012).
Gottesman, D., Kitaev, A. & Preskill, J. Encoding a qubit in an oscillator. Phys. Rev. A 64, 012310 (2001).
Bartlett, S. D., de Guise, H. & Sanders, B. C. Quantum encodings in spin systems and harmonic oscillators. Phys. Rev. A 65, 052316 (2002).
Monroe, C., Meekhof, D. M., King, B. E., Itano, W. M. & Wineland, D. J. Demonstration of a fundamental quantum logic gate. Phys. Rev. Lett. 75, 4714–4717 (1995).
Collaboration, L. S. et al. A gravitational wave observatory operating beyond the quantum shot-noise limit. Nature Phys. 7, 962–965 (2011).
Aasi, J. et al. Enhanced sensitivity of the LIGO gravitational wave detector by using squeezed states of light. Nature Photon. 7, 613–619 (2013).
Vlastakis, B. et al. Deterministically encoding quantum information using 100-photon Schrödinger’s cat states. Science 342, 607–610 (2013).
Hempel, C. et al. Entanglement-enhanced detection of single-photon scattering events. Nature Photon. 7, 630–633 (2013).
Hao-Sheng, Z., Ai-Qin, H., Qiong, L. & Le-Man, K. Direct measurement of squeezing in the motion of trapped ions. Chin. Phys. Lett. 22, 798–800 (2005).
Gerritsma, R. et al. Quantum simulation of the Dirac equation. Nature 463, 68–71 (2010).
Casanova, J., López, C. E., García-Ripoll, J. J., Roos, C. F. & Solano, E. Quantum tomography in position and momentum space. Eur. Phys. J. D 66, 1–5 (2012).
Kienzler, D. et al. Quantum harmonic oscillator state synthesis by reservoir engineering. Science 347, 53–56 (2015).
Caves, C. M. Quantum-mechanical noise in an interferometer. Phys. Rev. D 23, 1693–1708 (1981).
Yuen, H. P. Two-photon coherent states of the radiation field. Phys. Rev. A 13, 2226–2243 (1976).
Wineland, D. J. et al. Experimental issues in coherent quantum-state manipulation of trapped atomic ions. J. Res. Natl Inst. Stand. Technol. 103, 259–328 (1998).
Turchette, Q. A. et al. Decoherence and decay of motional quantum states of a trapped atom coupled to engineered reservoirs. Phys. Rev. A 62, 053807 (2000).
Breitenbach, G., Schiller, S. & Mlynek, J. Measurement of the quantum states of squeezed light. Nature 387, 471–475 (1997).
Ourjoumtsev, A., Jeong, H., Tualle-Brouri, R. & Grangier, P. Generation of optical ‘Schrödinger cats’ from photon number states. Nature 448, 784–786 (2007).
Meekhof, D. M., Monroe, C., King, B. E., Itano, W. M. & Wineland, D. J. Generation of nonclassical motional states of a trapped atom. Phys. Rev. Lett. 76, 1796–1799 (1996). Erratum. Phys. Rev. Lett. 77, 2346 (1996).
Leibfried, D., Blatt, R., Monroe, C. & Wineland, D. Quantum dynamics of single trapped ions. Rev. Mod. Phys. 75, 281–324 (2003).
Di Fidio, C. & Vogel, W. Damped Rabi oscillations of a cold trapped ion. Phys. Rev. A 62, 031802 (2000).
Mandel, L. Sub-Poissonian photon statistics in resonance fluorescence. Opt. Lett. 4, 205–207 (1979).
Haroche, S. & Raimond, J.-M. Exploring the Quantum: Atoms and Cavities and Photons (Oxford Univ. Press. (2006)).
Gerry, C. & Knight, P. Introductory Quantum Optics (Cambridge Univ. Press, 2005).
Acknowledgements
We thank J. Alonso and F. Leupold for comments on the manuscript, and F. Leupold, F. Lindenfelser, J. Alonso, M. Sepiol, K. Fisher and C. Flühmann for contributions to the experimental apparatus. We acknowledge support from the Swiss National Science Foundation under grant number 200021 134776, and through the National Centre of Competence in Research for Quantum Science and Technology (QSIT).
Author information
Authors and Affiliations
Contributions
Experimental data were taken by H.-Y.L., D.K. and L.d.C., using an apparatus primarily built by D.K., H.-Y.L. and B.C.K., and with significant contributions from L.d.C., V.N. and M.M. Data analysis was performed by H.-Y.L. and J.P.H. The paper was written by J.P.H. and H.-Y.L., with input from all authors. The study was conceived by J.P.H.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Extended data figures and tables
Extended Data Figure 1 Quasi-probability distributions for displaced-squeezed states in phase space using LDA and non-LDA.
a, c, e, The simulation results using LDA with different SDF durations. b, d, f, The results simulated using the full Hamiltonian.
Extended Data Figure 2 Coherence of cat states with fixed magnetic field noise.
The magnetic-field-induced energy-level shift of 1.5 kHz is used in this simulation. a, The duration of both SDF pulses is 60 μs. b, The duration of both SDF pulses is 120 μs. Dashed red and dash–dot green curves show the SDF aligned along the squeezed and anti-squeezed quadratures. The blue trace is for the SDF applied to a ground-state cooled ion.
Extended Data Figure 3 Coherence of cat states with a magnetic field fluctuation distribution.
With the assumption that the magnetic field exhibits a 50 Hz sinusoidal pattern with an amplitude of 2.2 mG, this plot shows the simulation results by taking an average over 100 samples on the field distribution. a, The duration of both SDF pulses is 60 μs. b, The duration of both SDF pulses is 120 μs. Definitions of the curve specification are the same as in Extended Data Fig. 2.
Extended Data Figure 4 Possible application of using SWESs for interferometry.
a, Use of squeezed-state wavepackets. b, Use of ground-state wavepackets. The first SDF pulse is used to create a spin–motion-entangled state. In the middle, a small phase shift Δθ is induced by shot-to-shot fluctuation in the oscillator frequency before the application of the second SDF pulse, which recombines the two distinct oscillator wavepackets.
Rights and permissions
About this article
Cite this article
Lo, HY., Kienzler, D., de Clercq, L. et al. Spin–motion entanglement and state diagnosis with squeezed oscillator wavepackets. Nature 521, 336–339 (2015). https://doi.org/10.1038/nature14458
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature14458
This article is cited by
-
Autonomous quantum error correction and fault-tolerant quantum computation with squeezed cat qubits
npj Quantum Information (2023)
-
Error correction of a logical grid state qubit by dissipative pumping
Nature Physics (2022)
-
Observation of a quantum phase transition in the quantum Rabi model with a single trapped ion
Nature Communications (2021)
-
Experimental quantum simulation of superradiant phase transition beyond no-go theorem via antisqueezing
Nature Communications (2021)
-
Large array of Schrödinger cat states facilitated by an optical waveguide
Nature Communications (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.