Abstract
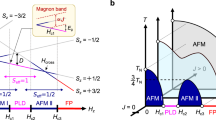
The low-temperature states of bosonic fluids exhibit fundamental quantum effects at the macroscopic scale: the best-known examples are Bose–Einstein condensation and superfluidity, which have been tested experimentally in a variety of different systems. When bosons interact, disorder can destroy condensation, leading to a ‘Bose glass’. This phase has been very elusive in experiments owing to the absence of any broken symmetry and to the simultaneous absence of a finite energy gap in the spectrum. Here we report the observation of a Bose glass of field-induced magnetic quasiparticles in a doped quantum magnet (bromine-doped dichloro-tetrakis-thiourea-nickel, DTN). The physics of DTN in a magnetic field is equivalent to that of a lattice gas of bosons in the grand canonical ensemble; bromine doping introduces disorder into the hopping and interaction strength of the bosons, leading to their localization into a Bose glass down to zero field, where it becomes an incompressible Mott glass. The transition from the Bose glass (corresponding to a gapless spin liquid) to the Bose–Einstein condensate (corresponding to a magnetically ordered phase) is marked by a universal exponent that governs the scaling of the critical temperature with the applied field, in excellent agreement with theoretical predictions. Our study represents a quantitative experimental account of the universal features of disordered bosons in the grand canonical ensemble.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Kramer, B. & MacKinnon, A. Localization: theory and experiment. Rep. Prog. Phys. 56, 1469–1564 (1993)
Fallani, L., Fort, C. & Inguscio, M. Bose-Einstein condensates in disordered potentials. Adv. At. Mol. Opt. Phys. 56, 119–160 (2008)
Giamarchi, T. & Schulz, H. J. Anderson localization and interactions in one-dimensional metals. Phys. Rev. B 37, 325–340 (1988)
Fisher, M. P. A., Weichman, P. B., Grinstein, G. & Fisher, D. S. Boson localization and the superfluid-insulator transition. Phys. Rev. B 40, 546–570 (1989)
Crowell, P. A., Van Keulz, F. W. & Reppy, J. D. Onset of superfluidity in 4He films adsorbed on disordered substrates. Phys. Rev. B 55, 12620–12634 (1997)
Sacépé, B. et al. Localization of preformed Cooper pairs in disordered superconductor. Nature Phys. 7, 239–244 (2011)
Bouadim, K., Loh, Y. L., Randeria, M. & Trivedi, N. Single- and two-particle energy gaps across the disorder-driven superconductor-insulator transition. Nature Phys. 7, 884–889 (2011)
Sanchez-Palencia, L. & Lewenstein, M. Disordered quantum gases under control. Nature Phys. 6, 87–95 (2010)
Deng, H. Haug, H. & Yamamoto, Y. Exciton-polariton Bose-Einstein condensation. Rev. Mod. Phys. 82, 1489–1537 (2010)
Giamarchi, T., Rüegg & Tchernyshyov, O. Bose-Einstein condensation in magnetic insulators. Nature Phys. 4, 198–204 (2008)
Nohadani, O., Wessel, S. & Haas, S. Bose-glass phases in disordered quantum magnets. Phys. Rev. Lett. 95, 227201 (2005)
Roscilde, T. & Haas, S. Quantum localization in bilayer Heisenberg antiferromagnets with site dilution. Phys. Rev. Lett. 95, 207206 (2005)
Roscilde, T. Field-induced quantum-disordered phases in S = 1/2 weakly coupled dimer systems with site dilution. Phys. Rev. B 74, 144418 (2006)
Manaka, H., Kolomiets, A. V. & Goto, T. Disordered states in IPA-Cu(ClxBr1–x)3 induced by bond randomness. Phys. Rev. Lett. 101, 077204 (2008)
Hong, T., Zheludev, A., Manaka, H. & Regnault, L.-P. Evidence of a magnetic Bose glass in (CH3)2CHNH3Cu(Cl0. 95Br0. 05)3 from neutron diffraction. Phys. Rev. B 81, 060410 (2010)
Zapf, V. S. et al. Bose-Einstein condensation of S = 1 nickel spin degrees of freedom in NiCl2-4SC(NH2)2 . Phys. Rev. Lett. 96, 077204 (2006)
Yin, L., Xia, J. S., Zapf, V. S., Sullivan, N. S. & Paduan-Filho, A. Direct measurement of the Bose-Einstein condensation universality class in NiCl2-4SC(NH2)2 at ultralow temperatures. Phys. Rev. Lett. 101, 187205 (2008)
Orignac, E., Giamarchi, T. & Le Doussal, P. A possible new phase of commensurate insulators with disorder: the Mott glass. Phys. Rev. Lett. 83, 2378–2381 (1999)
Prokof'ev, N. & Svistunov, B. Superfluid-insulator transition in commensurate disordered bosonic systems: large-scale worm algorithm simulations. Phys. Rev. Lett. 92, 015703 (2004)
Altman, E., Kafri, Y., Polkovnikov, A. & Refael, G. Phase transition in a system of one-dimensional bosons with strong disorder. Phys. Rev. Lett. 93, 150402 (2004)
Roscilde, T. & Haas, S. Mott glass in site-diluted S = 1 antiferromagnets with single-ion anisotropy. Phys. Rev. Lett. 99, 047205 (2007)
Zvyagin, S. A. et al. Magnetic excitations in the spin-1 anisotropic Heisenberg antiferromagnetic chain system NiCl2-4SC(NH2)2 . Phys. Rev. Lett. 98, 047205 (2007)
Zvyagin, S. A. et al. Spin dynamics of NiCl2-4SC(NH2)2 in the field-induced ordered phase. Phys. Rev. B 77, 092413 (2008)
Yin, L., Xia, J. S., Zapf, V. S. & Sullivan, N. S. &. Paduan-Filho, A. Magnetic susceptibility measurements at ultra-low temperatures. J. Low Temp. Phys. 158, 710–715 (2010)
Balabanyan, K. G., Prokof'ev, N. & Svistunov, B. Superfluid-insulator transition in commensurate one-dimensional bosonic system with off-diagonal disorder. Phys. Rev. Lett. 95, 055701 (2005)
Yu, R., Haas, S. & Roscilde, T. Universal phase diagram of disordered bosons from a doped quantum magnet. Europhys. Lett. 89, 10009 (2010)
Weickert, F. et al. Low temperature thermodynamic properties near the field-induced quantum critical point in DTN. Phys. Rev. B 85, 184408 (2012)
Kawashima, N. Quantum critical point of the XY model and condensation of field-induced quasiparticles in dimer compounds. J. Phys. Soc. Jpn 73, 3219–3222 (2004)
Yu, R. et al. Quantum critical scaling at a Bose-glass/superfluid transition: theory and experiment on a model quantum magnet. Preprint at http://arXiv.org/abs/1204.5409 (2012)
Acknowledgements
Work at the High Magnetic Field Laboratory at the Physics Institute of the University of São Paulo was supported in part by the Brazilian agencies FAPESP and CNPq. Measurements at the NHMFL High B/T and pulsed field facilities were supported by NSF grant DMR 0654118, by the State of Florida, and by the DOE. Work at LANL was supported by the NSF, and by the DOE's Laboratory Directed Research and Development programme under 20100043DR. C.F.M. acknowledges support by UEFISCDI (project RP-10). The numerical simulations were performed on the computer facilities of the NCCS at the Oak Ridge National Laboratories, and supported by INCITE Award MAT013 of the Office of Science, DOE. Further theory work was supported by the DOE (grant DE-FG03-01ER45908 and DE-FG02-05ER46240), the NSF (grant DMR-1006985) and by the Robert A. Welch Foundation (grant C-1411).
Author information
Authors and Affiliations
Contributions
R.Y., S.H. and T.R. performed the numerical simulations and the theoretical analysis; L.Y., N.S.S., J.S.X. and C.H. performed the susceptibility measurements; A.P.-F. and N.F.O. synthesized the samples and performed the d.c. magnetization measurements; A.S., C.F.M., F.W., R.M., E.-D.M. and V.S.Z. performed the specific heat measurements; and B.L.S. performed the X-ray measurements. V.S.Z. coordinated the experimental efforts and T.R. the theoretical ones. T.R. wrote the manuscript, with the contributions of all the authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
This file contains Supplementary Text and Data, Supplementary Figures 1-9 and additional references. (PDF 705 kb)
Rights and permissions
About this article
Cite this article
Yu, R., Yin, L., Sullivan, N. et al. Bose glass and Mott glass of quasiparticles in a doped quantum magnet. Nature 489, 379–384 (2012). https://doi.org/10.1038/nature11406
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature11406
This article is cited by
-
Field-controlled multicritical behavior and emergent universality in fully frustrated quantum magnets
npj Quantum Materials (2024)
-
Double dome structure of the Bose–Einstein condensation in diluted S = 3/2 quantum magnets
Nature Communications (2023)
-
A quantum magnetic analogue to the critical point of water
Nature (2021)
-
Emergent bound states and impurity pairs in chemically doped Shastry-Sutherland system
Nature Communications (2019)
-
Magneto-electric Effect and Dielectric Susceptibility Measurement Technique at Very Low Temperature
Journal of Low Temperature Physics (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.