Abstract
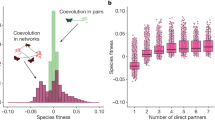
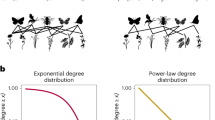
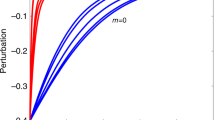
Complex networks of interactions are ubiquitous1 and are particularly important in ecological communities, in which large numbers of species exhibit negative (for example, competition or predation) and positive (for example, mutualism) interactions with one another. Nestedness in mutualistic ecological networks is the tendency for ecological specialists to interact with a subset of species that also interact with more generalist species2. Recent mathematical and computational analysis has suggested that such nestedness increases species richness3,4. By examining previous results and applying computational approaches to 59 empirical data sets representing mutualistic plant–pollinator networks, we show that this statement is incorrect. A simpler metric—the number of mutualistic partners a species has—is a much better predictor of individual species survival and hence, community persistence. Nestedness is, at best, a secondary covariate rather than a causative factor for biodiversity in mutualistic communities. Analysis of complex networks should be accompanied by analysis of simpler, underpinning mechanisms that drive multiple higher-order network properties.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Proulx, S. R., Promislow, D. E. L. & Phillips, P. C. Network thinking in ecology and evolution. Trends Ecol. Evol. 20, 345–353 (2005)
Almeida-Neto, M., Guimaraes, P., Guimaraes, P. R., Loyola, R. D. & Ulrich, W. A consistent metric for nestedness analysis in ecological systems: reconciling concept and measurement. Oikos 117, 1227–1239 (2008)
Bastolla, U. et al. The architecture of mutualistic networks minimizes competition and increases biodiversity. Nature 458, 1018–1020 (2009)
Thebault, E. & Fontaine, C. Stability of ecological communities and the architecture of mutualistic and trophic networks. Science 329, 853–856 (2010)
Saavedra, S., Stouffer, D. B., Uzzi, B. & Bascompte, J. Strong contributors to network persistence are the most vulnerable to extinction. Nature 478, 233–235 (2011)
Klein, A. M. et al. Importance of pollinators in changing landscapes for world crops. Proc. R. Soc. B 274, 303–313 (2007)
Bascompte, J., Jordano, P., Melian, C. J. & Olesen, J. M. The nested assembly of plant-animal mutualistic networks. Proc. Natl Acad. Sci. USA 100, 9383–9387 (2003)
Atmar, W. & Patterson, B. D. The measure of order and disorder in the distribution of species in fragmented habitat. Oecologia 96, 373–382 (1993)
Rezende, E. L., Lavabre, J. E., Guimaraes, P. R., Jordano, P. & Bascompte, J. Non-random coextinctions in phylogenetically structured mutualistic networks. Nature 448, 925–926 (2007)
Bastolla, U., Lassig, M., Manrubia, S. C. & Valleriani, A. Biodiversity in model ecosystems, I: coexistence conditions for competing species. J. Theor. Biol. 235, 521–530 (2005)
May, R. M. Stability and Complexity in Model Ecosystems. (Princeton Univ. Press, 1973)
Allesina, S. & Tang, S. Stability criteria for complex ecosystems. Nature 483, 205–208 (2012)
Flores, C. O., Meyer, J. R., Valverde, S., Farr, L. & Weitz, J. S. Statistical structure of host-phage interactions. Proc. Natl Acad. Sci. USA 108, E288–E297 (2011)
Kondoh, M., Kato, S. & Sakato, Y. Food webs are built up with nested subwebs. Ecology 91, 3123–3130 (2010)
Zhang, F., Hui, C. & Terblanche, J. S. An interaction switch predicts the nested architecture of mutualistic networks. Ecol. Lett. 14, 797–803 (2011)
Vermaat, J. E., Dunne, J. A. & Gilbert, A. J. Major dimensions in food-web structure properties. Ecology 90, 278–282 (2009)
Williams, R. J. Simple MaxEnt models explain food web degree distributions. Theor. Ecol. 3, 45–52 (2010)
Williams, R. J. Biology, methodology or chance? The degree distributions of bipartite ecological networks. PLoS ONE 6, e17645 (2011)
Wiggins, S. Introduction to Applied Nonlinear Dynamical Systems and Chaos. 2nd edn (Springer, 2003)
Zar, J. H. Biostatistical Analysis. 4th edn (Prentice Hall, 1999)
Long, J. S. Regression Models for Categorical and Limited Dependent Variables. (Sage Publications, 1997)
Acknowledgements
We thank D. Franks, D. Kelly, R. Law, D. Stouffer, C. Thomas and J. Tylianakis for discussions and constructive criticisms, and J.Williams for independent verification of numerical results. M.J.P., A.J. and J.W.P. were supported by the Royal Society of New Zealand Marsden Fund, grant number 08-UOC-034. J.W.P. acknowledges the support of the University of Canterbury Erskine Programme.
Author information
Authors and Affiliations
Contributions
All authors contributed equally to this work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
This file contains Supplementary Text and Data, Supplementary Tables 1-2, Supplementary Figures 1-8 and Supplementary References. (PDF 840 kb)
Rights and permissions
About this article
Cite this article
James, A., Pitchford, J. & Plank, M. Disentangling nestedness from models of ecological complexity. Nature 487, 227–230 (2012). https://doi.org/10.1038/nature11214
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature11214
This article is cited by
-
The Relative Importance of Environmental Filtering and Dispersal Limitation on the Multidimensional Beta Diversity of Desert Plant Communities Depends on Sampling Scales
Journal of Soil Science and Plant Nutrition (2023)
-
Plant-frugivore network simplification under habitat fragmentation leaves a small core of interacting generalists
Communications Biology (2022)
-
Ecological network complexity scales with area
Nature Ecology & Evolution (2022)
-
An ecological approach to structural flexibility in online communication systems
Nature Communications (2021)
-
Biodiversity decline of fish assemblages after the impoundment of the Three Gorges Dam in the Yangtze River Basin, China
Reviews in Fish Biology and Fisheries (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.