Abstract
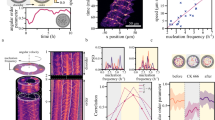
Spontaneous collective motion, as in some flocks of bird and schools of fish, is an example of an emergent phenomenon. Such phenomena are at present of great interest1,2,3,4,5 and physicists have put forward a number of theoretical results that so far lack experimental verification6,7,8. In animal behaviour studies, large-scale data collection is now technologically possible, but data are still scarce and arise from observations rather than controlled experiments. Multicellular biological systems, such as bacterial colonies or tissues9,10, allow more control, but may have many hidden variables and interactions, hindering proper tests of theoretical ideas. However, in systems on the subcellular scale such tests may be possible, particularly in in vitro experiments with only few purified components11,12,13. Motility assays, in which protein filaments are driven by molecular motors grafted to a substrate in the presence of ATP, can show collective motion for high densities of motors and attached filaments. This was demonstrated recently for the actomyosin system14,15, but a complete understanding of the mechanisms at work is still lacking. Here we report experiments in which microtubules are propelled by surface-bound dyneins. In this system it is possible to study the local interaction: we find that colliding microtubules align with each other with high probability. At high densities, this alignment results in self-organization of the microtubules, which are on average 15 µm long, into vortices with diameters of around 400 µm. Inside the vortices, the microtubules circulate both clockwise and anticlockwise. On longer timescales, the vortices form a lattice structure. The emergence of these structures, as verified by a mathematical model, is the result of the smooth, reptation-like motion of single microtubules in combination with local interactions (the nematic alignment due to collisions)—there is no need for long-range interactions. Apart from its potential relevance to cortical arrays in plant cells16,17 and other biological situations, our study provides evidence for the existence of previously unsuspected universality classes of collective motion phenomena.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Ballerini, M. et al. Interaction ruling animal collective behavior depends on topological rather than metric distance: evidence from a field study. Proc. Natl Acad. Sci. USA 105, 1232–1237 (2008)
Buhl, J. et al. From disorder to order in marching locusts. Science 312, 1402–1406 (2006)
Katz, Y., Tunstrøm, K., Ioannou, C. C., Huepe, C. & Couzin, I. D. Inferring the structure and dynamics of interactions in schooling fish. Proc. Natl Acad. Sci. USA 108, 18720–18725 (2011)
Lukeman, R., Li, Y.-X. & Edelstein-Keshet, L. Inferring individual rules from collective behavior. Proc. Natl Acad. Sci. USA 107, 12576–12580 (2010)
Sumpter, D. J. T. Collective Animal Behavior (Princeton Univ. Press, 2010)
Vicsek, T., Czirók, A., Ben-Jacob, E., Cohen, I. & Shochet, O. Novel type of phase transition in a system of self-driven particles. Phys. Rev. Lett. 75, 1226–1229 (1995)
Toner, J., Tu, Y. & Ramaswamy, S. Hydrodynamics and phases of flocks. Ann. Phys. 318, 170–244 (2005)
Ramaswamy, S. The mechanics and statistics of active matter. Annu. Rev. Condens. Mat. Phys. 1, 323–345 (2010)
Zhang, H. P., Be’er, A., Florin, E.-L. & Swinney, H. L. Collective motion and density fluctuations in bacterial colonies. Proc. Natl Acad. Sci. USA 107, 13626–13630 (2010)
Poujade, M. et al. Collective migration of an epithelial monolayer in response to a model wound. Proc. Natl Acad. Sci. USA 104, 15988–15993 (2007)
Nédélec, F. J., Surrey, T., Maggs, A. C. & Leibler, S. Self-organization of microtubules and motors. Nature 389, 305–308 (1997)
Surrey, T., Nédélec, F., Leibler, S. & Karsenti, E. Physical properties determining self-organization of motors and microtubules. Science 292, 1167–1171 (2001)
Loose, M., Fischer-Friedrich, E., Ries, J., Kruse, K. & Schwille, P. Spatial regulators for bacterial cell division self-organize into surface waves in vitro. Science 320, 789–792 (2008)
Schaller, V., Weber, C., Semmrich, C., Frey, E. & Bausch, A. R. Polar patterns of driven filaments. Nature 467, 73–77 (2010)
Butt, T. et al. Myosin motors drive long range alignment of actin filaments. J. Biol. Chem. 285, 4964–4974 (2010)
Yuan, M., Shaw, P. J., Warn, R. M. & Lloyd, C. W. Dynamic reorientation of cortical microtubules, from transverse to longitudinal, in living plant cells. Proc. Natl Acad. Sci. USA 91, 6050–6053 (1994)
Wasteneys, G. O. & Ambrose, J. C. Spatial organization of plant cortical microtubules: close encounters of the 2D kind. Trends Cell Biol. 19, 62–71 (2009)
Kagami, O. & Kamiya, R. Translocation and rotation of microtubules caused by multiple species of Chlamydomonas inner-arm dynein. J. Cell Sci. 103, 653–664 (1992)
Sakakibara, H., Kojima, H., Sakai, Y., Katayama, E. & Oiwa, K. Inner-arm dynein c of Chlamydomonas flagella is a single-headed processive motor. Nature 400, 586–590 (1999)
Ginelli, F., Peruani, F., Bär, M. & Chaté, H. Large-scale collective properties of self-propelled rods. Phys. Rev. Lett. 104, 184502 (2010)
Kudrolli, A., Lumay, G., Volfson, D. & Tsimring, L. S. Swarming and swirling in self-propelled polar granular rods. Phys. Rev. Lett. 100, 058001 (2008)
Peruani, F., Deutsch, A. & Bär, M. Nonequilibrium clustering of self-propelled rods. Phys. Rev. E 74, 030904(R) (2006)
Kikushima, K. & Kamiya, R. Clockwise translocation of microtubules by flagellar inner-arm dyneins. Biophys. J. 94, 4014–4019 (2008)
Riedel, I. H., Kruse, K. & Howard, J. A self-organized vortex array of hydrodynamically entrained sperm cells. Science 309, 300–303 (2005)
Tindemans, S. H., Hawkins, R. J. & Mulder, B. M. Survival of the aligned: ordering of the plant cortical microtubule array. Phys. Rev. Lett. 104, 058103 (2010)
Allard, J. F., Ambrose, J. C., Wasteneys, G. O. & Cytrynbaum, E. N. A mechanochemical model explains interactions between cortical microtubules in plants. Biophys. J. 99, 1082–1090 (2010)
Hess, H. et al. Molecular self-assembly of “nanowires” and “nanospools” using active transport. Nano Lett. 5, 629–633 (2005)
Schaller, V., Weber, C., Hammerich, B., Frey, E. & Bausch, A. R. Frozen steady states in active systems. Proc. Natl. Acad. Sci. USA 108, 19183–19188 (2011)
Dixit, R. & Cyr, R. Encounters between dynamic cortical microtubules promote ordering of the cortical array through angle-dependent modifications of microtubule behavior. Plant Cell 16, 3274–3284 (2004)
Acknowledgements
We thank H. Sakakibara, Y. Uchida and R. Nakamori for the preparation of the material and observations. They as well as H. Kitahata are also thanked for discussions. Y. Sumino is supported by a Grant-in-Aid for Research Activity Start-up (no. 23840019), Grant-in-Aid for Scientific Research (B) (no. 21340023) and Grant-in-Aid for Scientific Research (A) (no. 20244067). K.H.N. would like to acknowledge the support of a fellowship from the JSPS (no. 23-1819).
Author information
Authors and Affiliations
Contributions
K.O. discovered the phenomenon of vortex lattice formation described here and conceived and performed the experiments with Y. Shitaka. Y. Sumino, K.H.N., D.T. and H.C. conceived and designed the simulations. Y. Sumino, K.H.N. and H.C. performed and analysed the simulations. In vitro motility assays were carried out under the directions of K.O. Y. Sumino, K.H.N., Y. Shitaka, H.C., K.Y. and K.O. interpreted the data. Y. Sumino, K.H.N., H.C. and K.O. wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
This file contains Supplementary Methods and Supplementary Figures 1-3. The Supplementary Methods describe methods for experimental procedure, data analysis and numerical simulation. Figures display, density dependence of vortex pattern, phase diagram of mathematical model, and collision behavior on different dynein c density (and kinesin density). (PDF 618 kb)
Supplementary Movie 1
This movie shows formation process of vortex pattern, corresponding to figure 1a. The density of microtubule was 0.05 µm-2. Microtubules were homogeneously distributed initially. They formed stream with time and finally the stream made closed loop, vortex. (MOV 12020 kb)
Supplementary Movie 2
This movie shows internal structure a vortex pattern, corresponding to figure 2a. Only 0.1% of microtubules were prepared to be more fluorescent. In a stream, microtubules moved both directions, clearly indicating a vortex has nematic order. (MOV 20042 kb)
Supplementary Movie 3
This movie shows collision behavior of microtubules. The densities of dynein c used was 2500 μm-2. Density of the microtubules on the surface was approximately 0.1 microtubules per 100 μm2 suitable for observations of individual collisions. (MOV 16186 kb)
Supplementary Movie 4
This movie shows result of numerical simulation of our mathematical model in T=0 to T=2000, corresponding to Figure 5a. 2621440 particles were used in 512 × 512 area with periodic boundary condition. Other parameters are written in the main text and supplementary information1. The brightest region corresponds to the 15 particles in a unit area. Green and red colors corresponds to the density of particles moving clockwise (ω<0) and counterclockwise (ω>0), respectively. (MOV 12549 kb)
Rights and permissions
About this article
Cite this article
Sumino, Y., Nagai, K., Shitaka, Y. et al. Large-scale vortex lattice emerging from collectively moving microtubules. Nature 483, 448–452 (2012). https://doi.org/10.1038/nature10874
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature10874
This article is cited by
-
Self-enhanced mobility enables vortex pattern formation in living matter
Nature (2024)
-
Emergence of synchronised rotations in dense active matter with disorder
Communications Physics (2023)
-
Autonomous waves and global motion modes in living active solids
Nature Physics (2023)
-
Non-reciprocity across scales in active mixtures
Nature Communications (2023)
-
Spontaneous shock waves in pulse-stimulated flocks of Quincke rollers
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.