Abstract
The term ‘molecular magnet’ generally refers to a molecular entity containing several magnetic ions whose coupled spins generate a collective spin, S (ref. 1). Such complex multi-spin systems provide attractive targets for the study of quantum effects at the mesoscopic scale. In these molecules, the large energy barriers between collective spin states can be crossed by thermal activation or quantum tunnelling, depending on the temperature or an applied magnetic field2,3,4. There is the hope that these mesoscopic spin states can be harnessed for the realization of quantum bits—‘qubits’, the basic building blocks of a quantum computer—based on molecular magnets5,6,7,8. But strong decoherence9 must be overcome if the envisaged applications are to become practical. Here we report the observation and analysis of Rabi oscillations (quantum oscillations resulting from the coherent absorption and emission of photons driven by an electromagnetic wave10) of a molecular magnet in a hybrid system, in which discrete and well-separated magnetic  clusters are embedded in a self-organized non-magnetic environment. Each cluster contains 15 antiferromagnetically coupled S = 1/2 spins, leading to an S = 1/2 collective ground state11,12,13. When this system is placed into a resonant cavity, the microwave field induces oscillatory transitions between the ground and excited collective spin states, indicative of long-lived quantum coherence. The present observation of quantum oscillations suggests that low-dimension self-organized qubit networks having coherence times of the order of 100 μs (at liquid helium temperatures) are a realistic prospect.
clusters are embedded in a self-organized non-magnetic environment. Each cluster contains 15 antiferromagnetically coupled S = 1/2 spins, leading to an S = 1/2 collective ground state11,12,13. When this system is placed into a resonant cavity, the microwave field induces oscillatory transitions between the ground and excited collective spin states, indicative of long-lived quantum coherence. The present observation of quantum oscillations suggests that low-dimension self-organized qubit networks having coherence times of the order of 100 μs (at liquid helium temperatures) are a realistic prospect.
Similar content being viewed by others
Main
In the context of quantum computing, it was recently discussed how the decoherence of molecular magnet spin quantum bits could be suppressed, with reference to the discrete low spin clusters V15 and Cr7Ni (ref. 7; see also refs 8 and 14). In both systems, their low spin states cause weak environmental coupling7, making them candidates for the realization of a long-lived quantum memory. Measurement of the spin relaxation time τ2 in Cr7Ni was subsequently reported and found to be interestingly large15,16; however, the important Rabi quantum oscillations were not observed, probably because electronic and nuclear degrees of freedom were too strongly linked to each other. As these oscillations have until now only been observed in non-molecular spin systems (see, for example, refs 17–20), it has remained an open question whether quantum oscillations could in principle be realized in molecular magnets7,8. This question is now answered by our observation of quantum oscillations of the Rabi type in V15. The main reason for this success lies in the fact that the important pairwise decoherence mechanism7,8 associated with dipolar interactions could be strongly reduced.
Before discussing the observed quantum oscillations, we first briefly describe the magnetic/electronic structure of the  species as determined experimentally. Following the synthesis of the quasi-spherical mesoscopic cluster anion
species as determined experimentally. Following the synthesis of the quasi-spherical mesoscopic cluster anion  nearly two decades ago (ref. 11), the properties of this molecule have received considerable attention (see, for example, refs 1, 11, 14, 21–25). The V15 cluster with an ∼1.3 nm diameter exhibits an unique structure with layers of different magnetizations: a large central
nearly two decades ago (ref. 11), the properties of this molecule have received considerable attention (see, for example, refs 1, 11, 14, 21–25). The V15 cluster with an ∼1.3 nm diameter exhibits an unique structure with layers of different magnetizations: a large central  triangle is sandwiched by two smaller
triangle is sandwiched by two smaller  hexagons11 (Fig. 1). The 15 S = 1/2 spins are coupled by antiferromagnetic super-exchange and Dzyaloshinsky–Moriya (DM) interaction13,21,22,23,24,25 (see also refs 26, 27) through different pathways, which results in a collective low spin ground state with S = 1/2 (refs 12, 13, 24, 25).
hexagons11 (Fig. 1). The 15 S = 1/2 spins are coupled by antiferromagnetic super-exchange and Dzyaloshinsky–Moriya (DM) interaction13,21,22,23,24,25 (see also refs 26, 27) through different pathways, which results in a collective low spin ground state with S = 1/2 (refs 12, 13, 24, 25).
 .
. a, The cluster is shown in ball-and-stick representation (green, V; orange, As; red, O). The outer V6 hexagons are highlighted by thick green lines. A weak deviation from trigonal symmetry can be attributed to the water molecule located in the centre of the cavity (O of the encapsulated water molecule in purple) or/and to the presence of water in the lattice between molecules. The different types of V ions, namely V1, V2, V3, V1′ and V2′, are shown for the definition of different exchange pathways. b, Sketch showing the spin arrangement at low temperatures (three-spin approximation), emphasizing some of the exchange interaction pathways (J, J1, J2, J′). The coupling J0 between the spins of the inner triangle is not direct but results from different exchange pathways through the hexagons. The magnetic layer system is defined by one V3 triangle sandwiched by two V6 hexagons (for further details see text).
Energy spectrum calculations for the full cluster spin space give two S = 1/2 (spin doublet) ground states slightly shifted from each other by DM interactions, and an S = 3/2 (spin quartet) excited state; these states are ‘isolated’ from a quasi-continuum of states lying at energy E/kB ≈ 250 K above the S = 3/2 excited state. These low-lying energy states can be obtained with a good accuracy using the generally accepted three-spin approximation (valid below 100 K), in which the spins of the inner triangle are coupled by an effective interaction  mediated by the spins of the hexagons12,13,21,22,23,24,25 (Fig. 2 and Methods; J0 and J′ are shown in Fig. 1b).
mediated by the spins of the hexagons12,13,21,22,23,24,25 (Fig. 2 and Methods; J0 and J′ are shown in Fig. 1b).
These calculated diagrams used parameter values g ≈ 1.96, J0 ≈ -2.45 K, DZ ≈ 43 mK and DXY = 0 (see text for details). a, The magnetic field is parallel to the c axis. Whereas the orbital singlet 4A2 (S = 3/2) gives the superposition of the three transitions 1, 2, and 3, the orbital doublet 2E (S = 1/2) gives two inter-doublet transitions 4 and 6 which are basically allowed, as well as two intra-doublet transitions 5 and 7 (which are respectively allowed by transverse DM interactions and non-symmetrical exchange interactions due to a small deviation from the trigonal symmetry24 (Methods)). Second order zero-field splitting of 4A2 and small splitting of the lines 1, 2, and 3 is not shown. The MJ labels correspond to the quantization axis along the DM anisotropy field. b, Shown are the transitions 4, 5, 6, and 7 for the angle θ = 45° between the field and cluster C3-axis. The MJ labels correspond to the quantization axis along the field in the strong field limit. The boundaries of the measured resonance fields of Fig. 4 correspond to the field distribution given by the positions of labels 4, 5, 6 and 7 above the curves. The blue transitions correspond to S = 3/2; the red and the green transitions correspond to S = 1/2.
The spin hamiltonian of V15 can be written as:

where Dij is the antisymmetric vector of the DM interaction associated with the pair ij, and A is the hyperfine coupling constant of the 51V isotope (see below). The six components of Dij can be expressed in terms of two parameters, namely DZ (perpendicular to the plane) and DXY (in-plane). The DM interaction removes the degeneracy of the two low-lying doublets and produces a first order zero-field splitting  (plus small second order corrections)22,23,24,25. The excited (quartet) state shows only a second order splitting caused by a small inter-multiplet mixing through the in-plane component of DM coupling, that is,
(plus small second order corrections)22,23,24,25. The excited (quartet) state shows only a second order splitting caused by a small inter-multiplet mixing through the in-plane component of DM coupling, that is,  (refs 24, 25). The energy separation between the doublet states and quartet state is given by
(refs 24, 25). The energy separation between the doublet states and quartet state is given by  (refs 13, 21–25). Figure 2 shows the level scheme calculated by diagonalization of the hamiltonian (equation (1)), with only one free parameter DZ ≈ 43 mK adjusted to fit the positions of the measured resonances (a value close to that obtained from magnetization data13,21,24), and DXY = 0, a choice conditioned by the fact that the transverse DM component has a negligible effect on resonance fields below 0.5 T (this is important in the calculation of transition probabilities only). To ensure legibility, hyperfine interactions are not included in Fig. 2 (they simply broaden the levels).
(refs 13, 21–25). Figure 2 shows the level scheme calculated by diagonalization of the hamiltonian (equation (1)), with only one free parameter DZ ≈ 43 mK adjusted to fit the positions of the measured resonances (a value close to that obtained from magnetization data13,21,24), and DXY = 0, a choice conditioned by the fact that the transverse DM component has a negligible effect on resonance fields below 0.5 T (this is important in the calculation of transition probabilities only). To ensure legibility, hyperfine interactions are not included in Fig. 2 (they simply broaden the levels).
A new hybrid material, based on the use of a cationic surfactant—DODA  —as an embedding material for the anionic clusters, was developed for the present work (see Methods). The related frozen system contains V15 clusters integrated into the self-organized environment of the surfactant. The clusters—prepared according to ref. 11—were extracted from aqueous solution into chloroform by the surfactant DODA present in large excess. The surfactants, which wrap up the cluster anions, are amphiphilic cations, with their long hydrophobic tails pointing away from the cluster anions, enabling solubility in chloroform. The procedure ensures that the cluster anions cannot get into direct contact with one another; they are clearly separated by the surfactants (mean distance ∼13 nm).
—as an embedding material for the anionic clusters, was developed for the present work (see Methods). The related frozen system contains V15 clusters integrated into the self-organized environment of the surfactant. The clusters—prepared according to ref. 11—were extracted from aqueous solution into chloroform by the surfactant DODA present in large excess. The surfactants, which wrap up the cluster anions, are amphiphilic cations, with their long hydrophobic tails pointing away from the cluster anions, enabling solubility in chloroform. The procedure ensures that the cluster anions cannot get into direct contact with one another; they are clearly separated by the surfactants (mean distance ∼13 nm).
Electron paramagnetic resonance (EPR) experiments were performed on this hybrid material at ∼4 K using a Bruker E-580 X-band continuous-wave (CW) and pulsed spectrometer operating at 9.7 GHz. The CW-EPR spectrum, recorded at 16 K on a frozen sample, corresponds precisely to that obtained in the solid state in a previous study12. In particular, the resonance field shows the same profile and line-width (∼30 mT), compatible with the g-tensor values of a single crystal ( and
and  ). The measured transition width W ≈ 35 mT is directly connected with the energy E occurring in the expression of decoherence calculated for a multi-spin molecule7,8 (see below). Note that this transition width W should be associated with S = 3/2, the EPR spectrum being dominated by the excited quartet.
). The measured transition width W ≈ 35 mT is directly connected with the energy E occurring in the expression of decoherence calculated for a multi-spin molecule7,8 (see below). Note that this transition width W should be associated with S = 3/2, the EPR spectrum being dominated by the excited quartet.
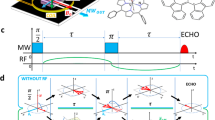
Rabi oscillations were recorded using a nutation pulse of length t, followed (after a delay greater than τ2) by a π/2-π sequence. Experimental results showed two different types of Rabi oscillations, corresponding to the resonant transitions 1, 2 and 3 for S = 3/2 spins, and 4, 5, 6 and 7 for S = 1/2 spins, here called ‘3/2’ and ‘1/2’, respectively (Fig. 3b and a, respectively). Although both types of oscillation are associated with the same collective degrees of freedom of the clusters, they show very different behaviour. In particular, the first type of Rabi frequency compares well with that of a single spin-3/2 system, whereas the Rabi frequency of the second type is much smaller than that of a single spin-1/2. This is a consequence of selection rules: the transition type ‘3/2’ is always allowed, whereas the transitions 5 and 7 of the ‘1/2’ type occur only due to transverse DM interactions or/and breaking of the C3 symmetry25 (Methods). Therefore we obtained Rabi oscillations with quite different frequencies,  and
and  , and a small ratio of transition probabilities (or intensities) R < 6 × 10-2 (Fig. 3, Methods). When the transition ‘1/2’ is excited (by a single excitation pulse), a whole spectrum of Rabi oscillations is generated. The frequency of the detected oscillation depends on the characteristics of the detection pulse, such as its length or its amplitude (Fig. 3). This spectrum is due to the presence of an avoided level crossing and the special selection rules; these are caused by the uniaxial anisotropy introduced by the DM interactions in the spin-frustrated (orbitally degenerate) ground state giving the overlapping transitions 4–7 (Fig. 2). The glassy character of the investigated frozen material is also relevant here; this material contains different cluster orientations, leading to a distribution of transverse field components, which gives a scattering of the coefficients of the states entering in the two-level wavefunctions
, and a small ratio of transition probabilities (or intensities) R < 6 × 10-2 (Fig. 3, Methods). When the transition ‘1/2’ is excited (by a single excitation pulse), a whole spectrum of Rabi oscillations is generated. The frequency of the detected oscillation depends on the characteristics of the detection pulse, such as its length or its amplitude (Fig. 3). This spectrum is due to the presence of an avoided level crossing and the special selection rules; these are caused by the uniaxial anisotropy introduced by the DM interactions in the spin-frustrated (orbitally degenerate) ground state giving the overlapping transitions 4–7 (Fig. 2). The glassy character of the investigated frozen material is also relevant here; this material contains different cluster orientations, leading to a distribution of transverse field components, which gives a scattering of the coefficients of the states entering in the two-level wavefunctions  and
and  and therefore a distribution of the Rabi frequencies
and therefore a distribution of the Rabi frequencies  (Fig. 2 and Methods). Whereas the splitting of the excited quartet state in a magnetic field is almost isotropic, the distribution function of the associated Rabi frequency is very narrow.
(Fig. 2 and Methods). Whereas the splitting of the excited quartet state in a magnetic field is almost isotropic, the distribution function of the associated Rabi frequency is very narrow.
a, Time evolution of the average spin 〈 Sz〉 after a spin-echo sequence. The ‘1/2’ type transition observed near the maximum of the corresponding resonance of Fig. 4 (B0, 336.0 mT) requires unusually large excitation power B1 = 1.1 mT and pulse length Tπ/2 = 64 ns. It corresponds to the transitions 4–7 of Fig. 2. The Rabi frequency ΩR = 4.5 MHz was selected by a detection pulse with characteristics B1 = 0.3 mT and Tπ/2 = 200 ns. b, The ‘3/2’ type transition with Rabi frequency ΩR = 18.5 MHz was excited near the maximum of the corresponding resonance of Fig. 4 (B0 = 354.3 mT). It requires excitation and detection pulses similar to those usually used for a single spin of 3/2 (B1 = 0.27 mT, Tπ/2 = 16 ns) and corresponds to the transitions 1–3 of Fig. 2. Inset, spin-echo intensity measured versus time for both oscillations. The coherence times τ2 obtained from exponential fits are inverse functions of the spin values: 800 ns for S = 1/2 (red) and 340 ns for S = 3/2 (blue). Superimposed oscillations, mainly observed on the ‘3/2’ type curve come from the precession of proton spins19. These oscillations correspond to only a weak perturbation of the Rabi coherence. Temperature, 4 K for all results shown.
An extension of the experiments shown in Fig. 3 to other values of the applied field showed that Rabi oscillations could be detected for each value of the applied field below 500 mT, while the transitions are inhomogeneously broadened. Figure 4 gives the result of a systematic investigation, consisting of the measurement of the spin-echo intensity at time t = 0 in a sweeping magnetic field. Two broad resonance distributions are observed, which correspond to the Rabi oscillations ‘3/2’ and ‘1/2’ of Fig. 3b and a, respectively, which were measured near the maxima H3/2 ≈ 357 mT and H1/2 ≈ 335 mT of the curves of Fig. 4. Whereas the nearly symmetrical type ‘3/2’ distribution shows resonances which are optimally excited by pulse durations and powers similar to those generally used for isolated 3/2 spins, the asymmetrical type ‘1/2’ distribution shows resonances requiring larger power and pulse length, confirming much smaller transition probabilities. The observed inhomogeneous widths (∼50 ± 10 mT) result from the existence of different transitions—that is 1 to 3 and 4 to 7 shifted by the longitudinal field components associated with the glassy character of the frozen solution. The width of the resonance of type ‘1/2’ (Fig. 4) fits the transition fields calculated from the hamiltonian (equation (1)) for the resonances 4 to 7 with limiting angles  and π/2 (Fig. 2), whereas the width of the resonance of type ‘3/2’ is simply given by the unique resonance field of transitions 1 to 3 (Fig. 2 a). In both cases, the 51V hyperfine interactions contribute equally to the resonance widths.
and π/2 (Fig. 2), whereas the width of the resonance of type ‘3/2’ is simply given by the unique resonance field of transitions 1 to 3 (Fig. 2 a). In both cases, the 51V hyperfine interactions contribute equally to the resonance widths.
The measurements were done in field sweep experiments for two excitation pulse configurations. The blue curve, corresponding to ‘3/2’ type transitions (obtained with the excitation pulse B1 = 0.27 mT and Tπ/2 = 16 ns), is nearly symmetrical and has a high transition probability. The red curve, corresponding to ‘1/2’ type transitions (obtained with the excitation pulse B1 = 1.1 mT and Tπ/2 = 64 ns), is asymmetrical and has a low probability (involving collective orbital degrees of freedom). The resonance fields form a ‘band’ due to random cluster orientations, while the corresponding distribution widths can be well explained by the dispersions of the resonance transitions 1–3 and 4–7.
To conclude, it was possible to entangle the 15 spins of a molecular magnet—a complex system which, formally speaking, entails a Hilbert space of dimension DH = 215 (Methods)—with photons by performing pulse EPR experiments on a frozen solution of randomly oriented and well separated clusters. Despite the complexity of the system11,12,13,14,21,22,23,24,25 (involving in a formal consideration dozens of cluster electrons and nuclear spins of 51V, 75As and 1H), long-lived Rabi oscillations10 were generated and selectively detected. An analysis, based on the widely used three-spin approximation of V15 (refs 12, 13, 21–25; the related interactions are mediated by the 12 other spins) gives a global interpretation of the results.
The observed coherence on the microsecond timescale seems to be mainly limited by the bath of nuclear spins. Each V15 cluster is correspondingly weakly coupled to 36 first-neighbour protons of the six DODA methyl groups distributed around the cluster, and to two water protons at the cluster centre. According to the charge (6-) of V15, six cationic DODA surfactants are relevant, with their positively charged parts (six dimethyl groups) attached to the O atoms of the cluster surface (see also ref. 28); the corresponding neutral hybrid just leads to the solubility in the organic solvent. The distance from the H atoms of a methyl group to a VIV is ∼0.45 nm. For this typical spin–proton distance, the half-width of the gaussian distribution of the coupling energy of a cluster/surfactant unit is E ≈ 3.5 mK, giving, for the level separation Δ ≈ 0.4 K (Fig. 2), the coherence time7,8  . The contribution of more distant neighbouring protons should reduce this value to a few microseconds. Regarding the decoherence effect from 51V, the transition width W ≈ 35 mK gives E = W/2 ≈ 17 mK and
. The contribution of more distant neighbouring protons should reduce this value to a few microseconds. Regarding the decoherence effect from 51V, the transition width W ≈ 35 mK gives E = W/2 ≈ 17 mK and  , suggesting that the observed decoherence of the S = 3/2 resonances is almost entirely caused by the 51V nuclear spins. The observed larger coherence time of the S = 1/2 transitions is presumably due to their smaller hyperfine coupling. In spite of the relatively high temperature of the measurement, the phonons’ decoherence7,8
, suggesting that the observed decoherence of the S = 3/2 resonances is almost entirely caused by the 51V nuclear spins. The observed larger coherence time of the S = 1/2 transitions is presumably due to their smaller hyperfine coupling. In spite of the relatively high temperature of the measurement, the phonons’ decoherence7,8  is strongly lowered due to the low spin and anisotropy values involved in the electron–phonon29,30 coupling
is strongly lowered due to the low spin and anisotropy values involved in the electron–phonon29,30 coupling  , giving
, giving  , that is,
, that is,  . Finally, the pairwise decoherence mechanism originating from electronic dipolar interaction7, which is usually considered as the most destructive, is nearly negligible, owing to the strong dilution of the clusters that results from the surfactant environment. This allows weak dipolar interactions only (∼0.5 μK) and very large coherence times (
. Finally, the pairwise decoherence mechanism originating from electronic dipolar interaction7, which is usually considered as the most destructive, is nearly negligible, owing to the strong dilution of the clusters that results from the surfactant environment. This allows weak dipolar interactions only (∼0.5 μK) and very large coherence times ( ). A comparison of the different decoherence mechanisms suggests that coherence times greater than 100 μs should be obtained in molecular magnets at liquid-helium temperatures if nuclear-spin-free molecules and deuterated surfactants are used.
). A comparison of the different decoherence mechanisms suggests that coherence times greater than 100 μs should be obtained in molecular magnets at liquid-helium temperatures if nuclear-spin-free molecules and deuterated surfactants are used.
The control of complex coherent spin states of molecular magnets—in which exchange interactions can be tuned by well defined chemical changes of the metal cluster ligand spheres—could finally lead to a way to avoid the ‘roadblock’ of decoherence. This would be particularly important in the case of self-organized one- or two-dimensional supramolecular networks, where well separated magnetic species could be addressed selectively, following different schemes already proposed for the molecular magnet option.
Methods Summary
When we refer to the three-spin approximation of V15 (refs 12, 13, 21–25), we consider the three spins located on each corner of the inner triangle (Fig. 1b). However these spins do not interact directly but via the other spins of the cluster. Strictly speaking, each hexagon contains three pairs of spins strongly coupled with J ≈ -800 K (‘dimers’) and each spin of the inner triangle is coupled to two of those pairs, one belonging to the upper hexagon and one belonging to the lower hexagon (J1 ≈ -150 K and J2 ≈ -300 K). This gives three groups of five spins with resultant spin S = 1/2 (superposition of ‘entangled’ states, coupled through inter-dimer hexagon superexchange J′ ≈ -150 K), showing that, in fact, the three-spin approximation involves all of the 15 spins of the cluster and therefore the Hilbert space has the dimension DH = 215 (DH for the three-spin system is 23). This approximation simplifies the evaluation of the low-lying energy levels of the 15 ‘entangled’ states of the V15 cluster. For  the S = 1/2 orbital doublet 2E, whose basis functions can be labelled by the quantum number of the total pseudo-angular momentum MJ = ML + MS , is associated with the pseudo-orbital momentum ML = +1 or ML = -1 (refs 24, 25). The allowed EPR transitions satisfy the subsequent selection rules:
the S = 1/2 orbital doublet 2E, whose basis functions can be labelled by the quantum number of the total pseudo-angular momentum MJ = ML + MS , is associated with the pseudo-orbital momentum ML = +1 or ML = -1 (refs 24, 25). The allowed EPR transitions satisfy the subsequent selection rules:  ,
,  , that is
, that is  for the inter-doublet transitions 4 and 6, and
for the inter-doublet transitions 4 and 6, and  ,
,  , that is
, that is  for the weak intra-doublet transition 5 whose transition probability is caused by a small intermultiplet mixing through the in-plane component of the DM coupling. The intensity of this transition is significantly increased when transition 7 becomes allowed due to a weak deviation from the C3 symmetry (Fig. 1). This also leads to an increased zero-field gap
for the weak intra-doublet transition 5 whose transition probability is caused by a small intermultiplet mixing through the in-plane component of the DM coupling. The intensity of this transition is significantly increased when transition 7 becomes allowed due to a weak deviation from the C3 symmetry (Fig. 1). This also leads to an increased zero-field gap  where δ is the parameter in the exchange shift δ S1S2.
where δ is the parameter in the exchange shift δ S1S2.
Online Methods
Sample synthesis
0.04 g (0.0175 mmol) of freshly prepared brown  obtained as reported10 was dissolved in 20 ml of degassed water. After addition of 25 ml of a (degassed) trichloromethane solution of [DODA]Br (1.10 g/1.75 mmol) the reaction medium was stirred under inert atmosphere. The stirring was continued until the olive-brown coloured aqueous layer turned colourless and the corresponding colour appeared in the organic phase. The organic layer was then quickly separated, put into an EPR tube and frozen to liquid nitrogen temperature. All operations were done in an inert atmosphere.
obtained as reported10 was dissolved in 20 ml of degassed water. After addition of 25 ml of a (degassed) trichloromethane solution of [DODA]Br (1.10 g/1.75 mmol) the reaction medium was stirred under inert atmosphere. The stirring was continued until the olive-brown coloured aqueous layer turned colourless and the corresponding colour appeared in the organic phase. The organic layer was then quickly separated, put into an EPR tube and frozen to liquid nitrogen temperature. All operations were done in an inert atmosphere.
Comparing Rabi frequencies
The frequency of the Rabi oscillations between two states 1 and 2 is given by6,7,8,19:

Here  is the Rabi frequency of a spin 1/2, B1 is the amplitude of the a.c. microwave fields, g ≈ 2 the Landé factor, S+ the ladder operator and
is the Rabi frequency of a spin 1/2, B1 is the amplitude of the a.c. microwave fields, g ≈ 2 the Landé factor, S+ the ladder operator and  ,
,  the wavefunctions associated with these states. The probability of a transition, defined as
the wavefunctions associated with these states. The probability of a transition, defined as  , is directly connected with its Rabi frequency:
, is directly connected with its Rabi frequency:

This allows one to evaluate the ratio (R) of the probabilities associated with two transitions (here the ‘3/2’ and ‘1/2’ types) from the measurement of their Rabi frequencies without the knowledge of their wavefunctions:

Using the values of the Rabi frequencies given in Fig. 3, one gets R ≈ (4.5/18.5)2 ≈ 5.9 × 10-2. The time Tπ/2, during which the excitation pulse is applied to induce a π/2 rotation, is by definition equal to 1/4ΩR (refs 6, 19), showing that equation (4) is equivalent to:

This gives another way to determine R. Using the Tπ/2 values given in Fig. 4 legend, one gets R ≈ (16/64)2 ≈ 6.2 × 10-2, which is very close to the first one and shows that the probability associated with the ‘1/2’ type transition is much smaller than the one associated with ‘3/2’.
References
Gatteschi, D., Sessoli, R. & Villain, J. Molecular Nanomagnets (Oxford Univ. Press, Oxford, UK, 2006)
Barbara, B. et al. Mesoscopic quantum tunneling of the magnetization. J. Magn. Magn. Mater. 140–144, 1825–1828 (1995)
Thomas, L. et al. Macroscopic quantum tunneling of magnetization in a single crystal of nanomagnets. Nature 383, 145–147 (1996)
Friedman, J. R. et al. Macroscopic measurements of resonant magnetization tunneling in high spin molecules. Phys. Rev. Lett. 76, 3830–3833 (1996)
Leuenberger, M. N. & Loss, D. Quantum computing in molecular magnets. Nature 410, 789–793 (2001)
Aharonov, D., Kitaev, A. & Preskill, J. Fault-tolerant quantum computation with long-range correlated noise. Phys. Rev. Lett. 96, 050504 (2006)
Stamp, P. C. E. & Tupitsyn, I. S. Coherence window in the dynamics of quantum nanomagnets. Phys. Rev. B 69, 014401 (2004)
Morello, A., Stamp, P. C. E. & Tupitsyn, I. S. Pairwise decoherence in coupled spin qubit networks. Phys. Rev. Lett. 97, 207206 (2006)
Prokof’ev, N. V. & Stamp, P. C. E. Theory of the spin bath. Rep. Prog. Phys. 63, 669–726 (2000)
Rabi, I. I. Space quantization in a gyrating magnetic field. Phys. Rev. 51, 652–654 (1937)
Müller, A. & Döring, J. A novel heterocluster with D 3-symmetry containing twenty-one core atoms: [AsIII 6VIV 15O42(H2O)]6- . Angew. Chem. Int. Edn Engl. 27, 1721 (1988)
Gatteschi, D., Pardi, L., Barra, A. L., Müller, A. & Döring, J. Layered magnetic structure of a metal cluster ion. Nature 354, 463–465 (1991)
Barbara, B. On the richness of supra-molecular chemistry and its openings in physics. J. Mol. Struct. 656, 135–140 (2003)
Wernsdorfer, W., Müller, A., Mailly, D. & Barbara, B. Resonant photon absorption in the low spin molecule V15 . Europhys. Lett. 66, 861–867 (2004)
Ardavan, A. et al. Will spin-relaxation times in molecular magnets permit quantum information processing? Phys. Rev. Lett. 98, 057201 (2007)
Wernsdorfer, W. A long-lasting phase. Nature Mater. 6, 174–176 (2007)
Mehring, M., Mende, J. & Scherer, W. Entanglement between an electron and a nuclear spin ½. Phys. Rev. Lett. 90, 153001 (2003)
Morton, J. J. L. et al. Bang–bang control of fullerene qubits using ultrafast phase gates. Nature Phys. 2, 40–43 (2006)
Bertaina, S. et al. Rare earth solid state qubits. Nature Nanotechnol. 2, 39–42 (2007)
Nellutla, S. et al. Coherent manipulation of electron spins up to ambient temperatures in Cr5+ (S = 1/2) doped K3NbO8 . Phys. Rev. Lett. 99, 137601 (2007)
Chiorescu, I., Wernsdorfer, W., Müller, A., Bögge, H. & Barbara, B. Butterfly hysteresis loop and dissipative spin reversal in the S = 1/2, V15 molecular complex. Phys. Rev. Lett. 84, 3454–3457 (2000)
De Raedt, H. D., Miyashita, S., Michielsen, K. & Machida, M. Dzyaloshinskii-Moriya interactions and adiabatic magnetization dynamics in molecular magnets. Phys. Rev. B 70, 064401 (2004)
Chaboussant, G. et al. Mechanism of ground-state selection in the frustrated molecular spin cluster V15 . Europhys. Lett. 66, 423–429 (2004)
Tarantul, A., Tsukerblat, B. & Müller, A. Static magnetization of V15 cluster at ultra-low temperatures: Precise estimation of antisymmetric exchange. Inorg. Chem. 46, 161–169 (2007)
Tsukerblat, B., Tarantul, A. & Müller, A. Low temperature EPR spectra of the mesoscopic cluster V15: The role of antisymmetric exchange. J. Chem. Phys. 125, 054714 (2006)
Dzyaloshinsky, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 4, 241–255 (1958)
Moriya, T. Anisotropic superexchange interactions and weak ferromagnetism. Phys. Rev. 120, 91–98 (1960)
Volkmer, D. et al. Towards nanodevices: Synthesis and characterization of the nanoporous surfactant-encapsulated keplerate (DODA)40(NH4)2[(H2O) n ⊂ Mo132O372(CH3COO)30(H2O)72]. J. Am. Chem. Soc. 122, 1995–1998 (2000)
Prokof'ev, N. V. & Stamp, P. C. E. Quantum relaxation of magnetisation in magnetic particles. J. Low Temp. Phys. 104, 143–210 (1996)
Hartmann-Boutron, F., Politi, P. & Villain, J. Tunneling and magnetic relaxation in mesoscopic molecules. Int. J. Mod. Phys. B 10, 2577–2637 (1996)
Acknowledgements
We acknowledge I. Chiorescu from NHMFL-FSU, Tallahassee, USA, for discussions. We thank M.-N. Collomb for help in processing samples for EPR measurements, and G. Desfonds for technical support. B.B. and A.M. thank the European Research Council for support through network projects MAGMANet, MolNanoMag, QueMolNa and INTAS; A.M. thanks the Deutsche Forschungsgemeinschaft and the Fonds der Chemischen Industrie for support; and B.T. and A.M. thank the German–Israeli Foundation for Scientific Research and Development for support.
Author information
Authors and Affiliations
Corresponding authors
Supplementary information
Supplementary Notes
The file contains Supplementary Notes. (PDF 97 kb)
Rights and permissions
About this article
Cite this article
Bertaina, S., Gambarelli, S., Mitra, T. et al. Quantum oscillations in a molecular magnet. Nature 453, 203–206 (2008). https://doi.org/10.1038/nature06962
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/nature06962
This article is cited by
-
Direct determination of high-order transverse ligand field parameters via µSQUID-EPR in a Et4N[160GdPc2] SMM
Nature Communications (2023)
-
Increasing the Hilbert space dimension using a single coupled molecular spin
Nature Communications (2021)
-
Exploiting chemistry and molecular systems for quantum information science
Nature Reviews Chemistry (2020)
-
Combining Molecular Spintronics with Electron Paramagnetic Resonance: The Path Towards Single-Molecule Pulsed Spin Spectroscopy
Applied Magnetic Resonance (2020)
-
Extraction of magnetic circular dichroism effects from blended mixture of magnetic linear dichroism signals in the cobalt/Scotch tape system
Scientific Reports (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.