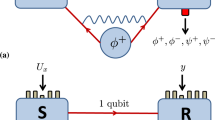
Abstract
Information—be it classical1 or quantum2—is measured by the amount of communication needed to convey it. In the classical case, if the receiver has some prior information about the messages being conveyed, less communication is needed3. Here we explore the concept of prior quantum information: given an unknown quantum state distributed over two systems, we determine how much quantum communication is needed to transfer the full state to one system. This communication measures the partial information one system needs, conditioned on its prior information. We find that it is given by the conditional entropy—a quantity that was known previously, but lacked an operational meaning. In the classical case, partial information must always be positive, but we find that in the quantum world this physical quantity can be negative. If the partial information is positive, its sender needs to communicate this number of quantum bits to the receiver; if it is negative, then sender and receiver instead gain the corresponding potential for future quantum communication. We introduce a protocol that we term ‘quantum state merging’ which optimally transfers partial information. We show how it enables a systematic understanding of quantum network theory, and discuss several important applications including distributed compression, noiseless coding with side information, multiple access channels and assisted entanglement distillation.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout


Similar content being viewed by others
References
Shannon, C. E. A mathematical theory of communication. Bell Syst. Tech. J. 27, 379–423, 623–656 (1948)
Schumacher, B. Quantum coding. Phys. Rev. A 51, 2738–2747 (1995)
Slepian, D. & Wolf, J. K. Noiseless coding of correlated information sources. IEEE Trans. Inf. Theory 19, 461–480 (1971)
Wehrl, A. General properties of entropy. Rev. Mod. Phys. 50, 221–260 (1978)
Horodecki, R. & Horodecki, P. Quantum redundancies and local realism. Phys. Lett. A 194, 147–152 (1994)
Cerf, N. J. & Adami, C. Negative entropy and information in quantum mechanics. Phys. Rev. Lett. 79, 5194–5197 (1997)
Einstein, A., Podolsky, B. & Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47, 777–780 (1935)
Bennett, C. H. et al. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 70, 1895–1899 (1993)
Schrödinger, E. Die gegenwärtige Situation der Quantenmechanik. Naturwissenschaften 23, 807–821, 823–828, 844–849 (1935)
Groisman, B., Popescu, S. & Winter, A. On the quantum, classical and total amount of correlations in a quantum state. Preprint at http://arXiv.org/quant-ph/0410091 (2004).
Horodecki, M. et al. Local versus non-local information in quantum information theory: formalism and phenomena. Phys. Rev. A 71, 062307 (2005)
Ahn, C., Doherty, A., Hayden, P. & Winter, A. On the distributed compression of quantum information. Preprint at http://arXiv.org/quant-ph/0403042 (2004).
Wyner, A. On source coding with the side information at the decoder. IEEE Trans. Inf. Theory 21, 294–300 (1975)
Terhal, B. M., Horodecki, M., DiVincenzo, D. P. & Leung, D. The entanglement of purification. J. Math. Phys. 43, 4286–4298 (2002)
Schumacher, B. & Nielsen, M. A. Quantum data processing and error correction. Phys. Rev. A 54, 2629–2635 (1996)
Shor, P. The quantum channel capacity and coherent information. MSRI Workshop on Quantum Computation (Berkeley, 2002); lecture notes available at http://www.msri.org/publications/ln/msri/2002/quantumcrypto/shor/1.
Lloyd, S. The capacity of the noisy quantum channel. Phys. Rev. A 55, 1613–1622 (1997)
Devetak, I . The private classical capacity and quantum capacity of a quantum channel. IEEE Trans. Inf. Theory 51(1), 44–55 (2005)
Yard, J., Devetak, I. & Hayden, P. Capacity theorems for quantum multiple access channels—Part I: classical-quantum and quantum-quantum capacity regions (2005). Preprint at http://arXiv.org/quant-ph/0501045 (2005).
DiVincenzo, D. P., et al. in Proc. 1st NASA Int. Conf. on Quantum Computing and Quantum Communication (ed. Williams, C. P.) LNCS 1509 247–257 (Springer, London, 1999)
Smolin, J. A., Verstraete, F. & Winter, A. Entanglement of assistance and multi-partite state distillation. Preprint at http://arXiv.org/quant-ph/0505038 (2005).
Lieb, E. H. & Ruskai, M. B. Proof of the strong subadditivity of quantum-mechanical entropy with an appendix by B. Simon. J. Math. Phys. 14, 1938–1941 (1973)
Devetak, I. & Winter, A. Relating quantum privacy and quantum coherence: an operational approach. Phys. Rev. Lett. 93, 080501 (2004)
Acknowledgements
This work was done at the Isaac Newton Institute (Cambridge) in August–December 2004 and we are grateful for the institute's hospitality. We thank W. Unruh for comments on an earlier draft of this paper. We acknowledge the support of EC grants RESQ, QUPRODIS and PROSECCO. M.H. was additionally supported by the Polish Ministry of Scientific Research and Information Technology, J.O. by the Cambridge-MIT Institute and Newton Trust, and A.W. by EPSRC's “IRC QIP”.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
Reprints and permissions information is available at npg.nature.com/reprintsandpermissions. The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Horodecki, M., Oppenheim, J. & Winter, A. Partial quantum information. Nature 436, 673–676 (2005). https://doi.org/10.1038/nature03909
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/nature03909
This article is cited by
-
Operational Interpretation of the Sandwiched Rényi Divergence of Order 1/2 to 1 as Strong Converse Exponents
Communications in Mathematical Physics (2024)
-
Slepian–Wolf coding with quantum side information
Quantum Information Processing (2023)
-
The QBIT theory of consciousness: Entropy and qualia
Integrative Psychological and Behavioral Science (2023)
-
Characterizing Coherence with Dynamical Entanglement
International Journal of Theoretical Physics (2023)
-
Theory Behind Quantum Error Correcting Codes: An Overview
Journal of the Indian Institute of Science (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.