Experimental control of optical helicity in nanophotonics

Abstract

An analysis of light–matter interactions based on symmetries can provide valuable insight, particularly because it reveals which quantities are conserved and which ones can be transformed within a physical system. In this context, helicity can be a useful addition to more commonly considered observables such as angular momentum. The question arises how to treat helicity, the projection of the total angular momentum onto the linear momentum direction, in practical experiments. In this paper, we put forward a simple but versatile experimental treatment of helicity. We then apply the proposed method to the scattering of light by isolated cylindrical nanoapertures in a gold film. This allows us to study the helicity transformation taking place during the interaction of focused light with the nanoapertures. In particular, we observe from the transmitted light that the scaling of the helicity transformed component with the aperture size is very different to the direct helicity component.

Introduction

Electromagnetic scattering problems may generally possess a high level of complexity. However, the presence of symmetries offers an excellent starting point to simplify and understand them better. To this end, it is important to consider the connection between symmetries and conserved quantities.¹ Such a framework enables both the explanation and prediction of certain phenomena, since they can be isolated from each other and attributed to their respective causes. One may take advantage of these ideas when designing an experiment to probe optical properties of a scatterer, by preparing the incident field such that it probes the particular property to be studied. An analysis in terms of symmetries and conserved quantities is also fruitful for nanophotonics experiments typically described as exhibiting conversion between spin and orbital angular momenta. In particular, such analysis can be achieved in terms of helicity and total angular momentum.² As opposed to the spin and orbital angular momentum description, this approach presents a direct link with symmetries. Total angular momentum is connected with rotational symmetry, so when a scatterer possesses rotational invariance, the corresponding components of the angular momentum of the electromagnetic field are conserved. Similarly, as we will explain below, helicity is connected with electromagnetic duality.

Compared to the total angular momentum, helicity, the projection of the total angular momentum onto the linear momentum direction,³ is a less studied observable in the context of symmetries and conserved quantities. Its definition is perhaps most easily understood in the plane wave decomposition of an electromagnetic field, where it is associated with the handedness of circular polarization of each plane wave with respect to its momentum vector. For an electromagnetic field to be in an eigenstate of helicity, it must fulfill that each of the plane waves composing the total field has the same handedness of circular polarization. From this intuitive description, it is easy to realize that in real space, the helicity of a general electromagnetic field does not bear a simple relationship with the polarization components of the electric field. As we will show below, the important case of collimated beams is an exception to this rule: collimated beams that are eigenstates of helicity can be described to a good approximation as circularly polarized beams with their handedness given by the eigenvalue of helicity.

The transformation connected with helicity is electromagnetic duality, the action of which is to mix the roles of electric and magnetic fields.^4,5 Remarkably, unlike the symmetries corresponding to linear and angular momentum, a system is strictly dual, that is, it has duality symmetry, depending only on its material properties rather than its geometry: in piecewise homogeneous and isotropic media, symmetry under duality is achieved if and only if the ratio of the electric permittivity and magnetic permeability, and hence, the geometry-independent intrinsic impedance, is constant for all subdomains.^2,6 Under such conditions, the helicity of the electromagnetic field must necessarily be conserved. In general, this does not imply zero scattering, but simply that no component with changed helicity is present in the scattered field. Using helicity, the study of the electromagnetic helicity in interactions with matter provides us with a new source of information: the electric and magnetic properties of the material system. Generally speaking, the transformation of electromagnetic helicity modes provides us with information about the helicity multipolar moments of the structure,⁷ which are constructed as the sum or differences of the well-known electric and magnetic multipolar moments. Naturally, to really add helicity to our toolkit, we need to develop experimental methods of preparing, manipulating and measuring helicity states of light.

In this paper, we present an experimental method to control the helicity of a light beam along with the necessary theoretical framework. The method is then applied to the experimental study of scattering of light by a cylindrical nanoaperture in a gold film. The transmission of light through isolated nanoholes was first studied in the seminal paper of Bethe⁸ and is now understood to be crucially affected by the effect of localized plasmons and surface modes at the metal–dielectric interfaces.⁹ Applications of this kind of nanostructures include optical trapping,¹⁰ funneling of light¹¹ and reshaping of optical fields.¹² The nanoaperture is also an interesting target in the proposed context of symmetries because of the geometrical symmetry our system presents. In contrast, it does not possess duality symmetry, which results in a transformation of the helicity of light upon scattering. In our experiment, we will concentrate on this aspect of the light–matter interaction: helicity transformation induced by the nanoapertures.

Materials and methods

Helicity has its simplest interpretation in momentum space rather than real space. As a result, the experimental control of helicity is a daunting task for a general electromagnetic field. However, for the special case of collimated light beams, the helicity content of the field can be simply controlled through the polarization of the field, with a helicity of ±1 corresponding to left/right circular (LC/RC) polarization. This means that with conventional optical elements, we can prepare a collimated beam which is arbitrarily close to a helicity eigenstate. It is also possible to perform projective measurements on a collimated beam in a similar manner by selecting the different circular polarization modes. Obviously, it is not always sufficient to remain in the paraxial regime. In order to manipulate light while preserving its helicity, it is necessary to use dual systems. Yet, at optical frequencies, it is very difficult to find a material with an intrinsic impedance matching that of air or vacuum. Alternatively, the use of metamaterials optimized to fulfill this duality symmetry condition would offer the most direct way to manipulate a light beam and at the same time guaranteeing that the helicity of the field is maintained. However, although perfect duality symmetry is impossible to achieve without such a material, some systems can be designed in such a way that helicity is preserved to a very good approximation.^13,14 In particular, microscope objectives designed to fulfill the aplanatic lens model do not change the helicity of light:^2,15 an effectively dual response is restored by special antireflection coatings. The following key outcomes make the experimental handling of helicity simple: (i) helicity can be manipulated and measured for collimated light beams through the polarization of the field; and (ii) using microscope objectives, transformation between paraxial and non-paraxial regimes without changing the helicity content is possible. The remainder of this section is structured as follows: first we introduce a type of Bessel beams where the electromagnetic field is in an eigenstate of helicity; then we consider the impact of experimental errors on helicity; and finally we present the experiment for the particular study of scattering by single circular nanoapertures in terms of helicity changes.

As experiments in optics often involve cylindrically symmetric beams, whether collimated or not, it is convenient to use the cylindrically symmetric Bessel beams as a basis set for electromagnetic fields in a theoretical description. Bessel modes can be written as two types of vector wave functions $\left({\text{C}}_{m{p}_z}\text{and}{\text{D}}_{m{p}_z}\right)$ which are simultaneously eigenstates of the energy given by the magnitude of the wavevector k, the z components of the linear momentum (i.e., $P_z{\text{C}}_{m{p}_z}=p_z{\text{C}}_{m{p}_z}$, $P_z{\text{D}}_{m{p}_z}=p_z{\text{D}}_{m{p}_z}$) and angular momentum (i.e., $J_z{\text{C}}_{m{p}_z}=m{\text{C}}_{m{p}_z}$, $J_z{\text{D}}_{m{p}_z}=m{\text{D}}_{m{p}_z}$), and also the helicity ($\Lambda {\text{C}}_{m{p}_z}=-{\text{C}}_{m{p}_z}$ and $\Lambda {\text{D}}_{m{p}_z}=+{\text{D}}_{m{p}_z}$, respectively).² The expressions for these functions are given below. We use cylindrical coordinates [ρ,θ,z] for the spatial variables and the helical basis for the vectorial character of the fields, where , . An implicit harmonic exp(−i ω t) dependence is assumed.

where , J_m(⋅) are the Bessel functions of the first kind, the amplitude , and B_±=(k±p_z). These modes form a complete orthonormal basis of transverse Maxwell fields.

In the collimated limit, when (p_z≈k so that B₊ → 2 and B₋ → 0), both ${\text{C}}_{m{p}_z}$ and ${\text{D}}_{m{p}_z}$ approach pure RC and LC polarized modes, respectively:

The other polarization components (the opposite circular and the longitudinal component) are strongly attenuated in the collimated regime. The error in the intensity that we are making with this approximation is of the order (p_ρ/k)². This asymptotic property allows us to prepare and analyze light beams with well defined helicity using simple optical elements. In the remainder of the paper, we will use the term ‘well defined’ to refer to eigenstates of a linear operator. Experimentally, when the light can be described as a mode which is an eigenstate of that linear operator, except for possible negligible deviations caused by experimental imperfections, we will typically mention that the value of that operator is ‘well defined’.

Equations (2) and (3) indicate that, as mentioned earlier, in order to control the helicity content of a collimated light beam we just need to control the polarization of the field. For example, let us consider our experimental set-up of Figure 1a. We start with a collimated Gaussian beam with diameter w=5 mm. We use a linear polarizer and a quarter waveplate after the laser source in order to obtain a collimated LC polarized Gaussian beam. If we decompose such beam with the collimated modes of Equations (2) and (3), the ${\text{D}}_{m{p}_z}$ components will dominate because of the polarization selectivity of the linear polarizer followed by the quarter waveplate. The RC/LC polarization intensity ratio of a Gaussian beam with well defined Λ=+1 will be of the order (w k)⁻⁴,¹⁶ which in our case would be of the order of 10⁻¹⁹. A comparison of this figure with the typical extinction ratios of commercial polarizers, 10⁻⁵, indicates that the polarizer is the limiting factor when preparing a collimated beam with well defined helicity.

Figure 1

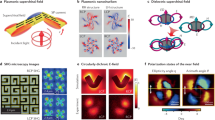
(a) Experimental set-up. An incoming collimated beam is circularly polarized with a set of waveplates and focused to address the isolated nanohole, which is centered with respect to the beam with a nanopositioner. The transmitted light is then collected and analyzed with another set of waveplates and a CCD camera. (b) Sketch of the concept behind the experiment. Light with a well-defined helicity, represented by a red propeller, impinges on a cylindrically symmetric aperture in a thin metallic film. The output light is analyzed in terms of its helicity content, represented as red propellers when it is the same as the incident helicity, or blue ones with opposite handedness when the helicity is the opposite to the incident one. (c) SEM image of the nanoapertures. CCD, charge-coupled device; SEM, scanning electron microscope.

After the polarizer and waveplate, we have prepared an electromagnetic field which is a superposition of only D-type Bessel beams. The amplitudes of the ${\text{D}}_{m{p}_z}$ for different m and p_z will be given by the shape of our beam. In particular, if the collimated beam is cylindrically symmetric, such as a Gaussian beam or the set of Laguerre–Gaussian modes, then the superposition of D-type Bessel modes will only contain terms with a single m. The value of m will then control the azimuthal phase of the field, as seen in Equation (3). A LC Gaussian beam does not contain any azimuthally varying phase in its dominant polarization vector. As a result, only terms with m=1 are possible in its expansion when Λ=+1. It is then quite clear from these theoretical considerations that controlling the circular polarization of a collimated beam allows for the preparation of light beams with sharp values of J_z and Λ. If such light with other J_z values is desired, holograms, spatial light modulators or similar can be used in conjunction with polarization controlling elements. Another option would be the use of q-plates, which allow for the control of the helicity and angular momentum with the same device.¹⁷ In order to measure the helicity content of a collimated beam, it is possible to use a quarter waveplate and a linear polarizer in two orthogonal settings.

While preparation and measurement are performed on collimated beams, where the approximations of Equations (2) and (3) hold, the actual interaction of light with the target may happen between two microscope objectives. For example, the first one focuses the incident beam onto the target from one side and the second one collects and collimates the output scattered field from the other side. Assuming that the two microscope objectives work as aplanatic lenses,¹⁸ they will not affect the helicity state of the light beam.¹⁵ As a consequence, by using simple preparation methods shown above, it is possible to illuminate a target with a strongly focused beam possessing well defined helicity Λ. The experimental error in the preparation of such highly focused beam with well defined values of J_z and Λ is mainly due to, in order of importance, the diffractive elements used to prepare the azimuthal phase, the extinction ratio of the polarizers and the transmissivities of the lenses for different polarizations (given by the antireflection coatings). For low values of m, microscope objectives are corrected to reduce mode mixing. In our experiment, such mixing was found to be comparable to the extinction ratio of the polarizers.

In this experiment, we are interested in the helicity change induced by the scattering of light from our target. For this reason, we choose an incident beam with well defined Λ=1, and to simplify the resulting field, we also ensure that the incident field has well defined J_z=1. The wavelength of the light is also fixed and unchanged during the experiment, at 633 nm. In contrast, the z component of the linear momentum does not have a sharp value since we are focusing the light. In terms of Bessel beams, our field incident on the nanoaperture can be written as a superposition of ${\text{D}}_{1p_z}$ functions, which all have Λ=1 and J_z=1, with different p_z values. The transformation of a light beam interacting with the target can be represented by a transfer matrix between Bessel modes $({\text{C}}_{m{p}_z},{\text{D}}_{m{p}_z})$. Since for our nanophotonics experiment the transformation leaves the angular momentum invariant, the transfer between Bessel modes is only allowed between modes with the same index m. We therefore expect that the transmitted light will consist of ${\text{D}}_{1p_z}$ (which have Λ=1, J_z=1) and ${\text{C}}_{1p_z}$ (which have Λ=−1, J_z=1), and are particularly interested in the mode consisting of ${\text{C}}_{1p_z}$ functions, which we select after collimating the scattered field by means of a quarter waveplate and polarizer. Such helicity change observed by the measurement apparatus is attributed to the interaction of the light beam with the target. The presence of a vortex of charge two (the mode ${\text{C}}_{1p_z}$ contains an exp (2iθ) term as can be seen from Equation (2) is a signature of angular momentum preserving and helicity changing scattering.²

The experiment was carried out on a set of isolated nanoapertures of different sizes, which were milled with a focused ion beam in a gold layer of 200 nm, deposited on top of a 1 mm thick glass substrate. A total of 212 different apertures with diameters ranging from 150 to 580 nm were used. Using a scanning electron microscope, we carefully measured the diameters of all the apertures and post selected the apertures presenting an ellipticity between 0 and 0.1. We individually probed the nanoapertures with a continuous wave laser (λ₀=633 nm). The preparation of the probing beam was done as follows. First, we collimated the laser beam and then used a set of linear polarizers (extinction ratio of 5×10⁻⁵) and waveplates to ensure a LC polarized light beam. As detailed previously, when this collimated field is decomposed in modes that are eigenstates of J_z and Λ, the components with J_z=1, Λ=1 are dominant. This collimated helicity field was subsequently focused with a microscope objective with a numerical aperture of 0.5. Since the transformation of an aplanatic lens preserves helicity, we were able to generate a focused electromagnetic field with a well defined helicity. The focused field was then allowed to interact with one of the isolated nanoapertures. We carefully positioned the nanoaperture on the symmetry axis of our optical system by means of a set of piezo-stages. Subsequently, the scattered light was collected and collimated with another microscope objective of numerical aperture=0.9. Once again, this lens did not affect the helicity of the beam, and as such, after collimation, we were able to analyze the helicity with another set of waveplates and polarizers. In this way, we obtained two very different spatial profiles for fields with J_z=1, Λ=1 and J_z=1, Λ=−1. The light was detected with a charge-coupled device camera.

Results and discussion

Our results show that the transmitted light always contains a transformed helicity component. This can be seen in Figure 2a, where we plot the power ratio between the two transmitted helicities, γ, as a function of the aperture diameters, d. The smallest conversion we measured was for the largest holes, γ₅₈₀=0.08±0.02. In contrast, the helicity transformation measured in the same sample through the glass alone, corresponding to an infinite aperture, is γ_glass≈10⁻³. Also, the helicity transformation by the focusing and collimating lenses alone was even smaller, of the order of γ_lens≈10⁻⁴, which is consistent with the fact that perfect aplanatic lenses should preserve helicity. In Figure 2b, we display the typical spatial patterns for the two output helicities of the light scattered from a perfect cylindrical aperture, as calculated with a semi-analytical method.¹⁹ We numerically checked that this output conserves angular momentum but, as can be seen, breaks helicity conservation (duality symmetry).

Figure 2

Helicity transformations through nanoapertures. (a) Dependence of the ratio of transmitted helicities on the aperture size. All points correspond to highly symmetrical apertures, the sizes of which were measured with a SEM. (b) Numerically calculated spatial pattern for the direct and transformed helicity fields transmitted through a cylindrical aperture of 300 nm. SEM, scanning electron microscope.

In order to test that our experimental results are consistent with the transformation of helicity and simultaneous conservation of angular momentum, we analyze the charge-coupled device images. In Figure 3, we show typical experimental results and their comparison with numerical calculations for two different aperture sizes. In the left column (Figure 3a and 3d), we show the components of the output field with the same helicity as the input, Λ₊. The observed field pattern is a typical Airy pattern arising from the subwavelength dimensions of the nanoaperture and the finite numerical aperture of the collection microscope objective, as expected from Figure 2b. On the other hand, the central column (Figure 3b and 3e) shows the corresponding fields with opposite helicity, Λ₋. The absence of singularities in Figure 3a and 3d, and the presence of two singularities in Figure 3b and 3e, are consistent with the theoretical considerations presented in the Materials and Methods section.

Figure 3

Projective measurement of helicity. Upper (lower) row shows the results for an aperture of 500 nm (300 nm). (a, d) Experimental results of transmitted light with helicity identical to the incident light. (b, e) Experimental results of transmitted light with opposite helicity. The cylindrical asymmetries are due to the finite extinction ratio of the polarizers. This is clearly seen with the numerically simulated patterns (c, f), where the asymmetry appears only after including the experimental parameters of the optical components used.

The differences between our experimental results and the ideal case of Figure 2b for the helicity transformed transmission are due to the finite extinction ratios of our polarizers. We now discuss this assertion. First of all, electromagnetic modes that are eigenstates of J_z have to be cylindrically symmetric. Additionally, from Equations (2) and (3), it can be seen that for collimated beams with eigenvalue of J_z=1 there are two cases, depending on the helicity. In the dominant polarization, the directly transmitted helicity mode has no phase singularity, and the helicity transformed mode has a second order singularity. Such a vortex of charge two is characteristic for an angular momentum preserving and helicity changing scattering, as explained in more detail elsewhere.² This is consistent with the experimental images of Figure 3. In practice, we could not avoid a small leakage from the unchanged helicity to the transformed helicity, when imaging the transformed helicity. As a result of such a superposition, the second order singularity splits into two singularities of order one. Thus, the intensity pattern is no longer cylindrically symmetric. In order to prove this point, we show in Figure 3c and 3f the coherent superposition of numerically calculated images of unmixed modes (as those of Figure 2b), with relative amplitudes given by the extinction ratios of our set of polarizers, 5×10⁻⁵. Given that the imperfections in the polarization controlling elements are the same for all apertures, one would expect that its effect should be smaller for those scatterers with a higher γ. This is indeed the case seen in Figure 3, which shows a smaller spatial separation of the singularities for the smaller aperture. The helicity transfer for the 500 nm aperture, γ₅₀₀=0.07±0.01, is a factor of 2.3, smaller than that for the 300 nm aperture, γ₃₀₀=0.16±0.03. We conclude that our measurements are consistent with the fact that in our system the angular momentum is conserved, but helicity is not.

According to the ideas presented in this paper, the observed helicity change implies that electromagnetic duality is broken in our samples. This is to be expected because we do not have equal intrinsic impedances in each subdomain. Light–matter interactions in which duality is broken, whether the scatterer is a metal or dielectric, would generally lead to non-conservation of helicity. While the conservation of helicity only depends on the contrast in the optical properties of the materials, when the duality symmetry is broken, the amount of helicity transformation depends on all the other characteristics of the scatterer. This is evident from the results displayed in Figure 2a, where the helicity transfer is seen to depend on the aperture size, with the material properties unchanged. In order to identify the exact mechanism of duality breaking in our experiment, it is instructive to first consider the multilayer system air–glass–gold–air without the nanoaperture. Duality is obviously broken by just the multilayer alone, but the helicity transfer in the absence of the nanoaperture is very small. Our numerical calculations show helicity transfers around 4×10⁻⁴ for our collection objective, assuming perfectly helicity preserving lenses. This value is consistent with the helicity change obtained through the glass substrate only (γ_glass≈10⁻³). The experimental observation of much higher transformation ratios must hence be tied to the nanoapertures.

The transmission and reflection in a planar multilayer system is best studied using plane waves. For a single plane wave with momentum k, the two helicity states are the two states of circular polarization, and can be obtained by linear combination of its s (transverse electric) and p (transverse magnetic) components: s±p. See [2, app. A] for a general derivation of this relationship, which also applies to multipolar fields and Bessel beams. Different scattering coefficients for s and p will hence mix the two helicity modes. A similar idea has recently been applied to the analysis of resonances in spheres,²⁰ where the fields are most suited to a multipolar decomposition. Returning to the planar multilayer, if the system presents a resonance for either s or p, the helicity transfer will be enhanced in its vicinity: a pure s or pure p mode is mirror symmetric and consists of an equal weight combination of the two helicities, hence strongly breaking helicity conservation (duality symmetry) when excited by a field with well defined helicity. Our system indeed presents several resonances for non-propagating modes.¹⁹ In the case of our multilayer structure, surface modes present such resonances that can be excited through the scattering of the incident field by the nanoaperture. Since they have equal contributions from the two helicities, this produces an asymmetric response of the surface modes with regard to the transmitted s- and p-polarized components. This additional electromagnetic asymmetry dramatically enhances the helicity transfer, even in the propagating modes, and makes it experimentally detectable. According to this explanation, the helicity transfer should increase for modes in the proximity of the resonance, i.e., for large transversal momenta. This actually explains the trend in Figure 2 that smaller holes present a larger γ value: smaller holes have a higher coupling to large transversal momenta, and in particular to the surface modes. We can then conclude that the nanoaperture plays a crucial role for the helicity transfer because it allows the coupling of the incident field to resonances of the multilayer structure.

An interesting matter of discussion is how the transmitted power scales with the aperture size. A review of several works covering this question has been given by Garcia-Vidal et al.²¹ In our experiment, we are studying the helicity modes which the transmitted field is composed of. In addition to the ratio of transformed to unchanged helicity powers from Figure 2, we have also analyzed the scaling of the different components of the transmitted field ${\text{D}}_{1p_z}$ and ${\text{C}}_{1p_z}$, finding a considerably different scaling law for the direct helicity component and the opposite one, as shown in Figure 4. One of the potential reasons for this difference between unchanged and changed helicity components may be the dominant multipolar moments that are at play for each component. The difference is especially interesting considering the behavior expected for the limit of very small hole diameters: the scaling with aperture size of the power transmitted in the limit of very small holes, albeit for the case of an infinitely thin perfect electric conductor, was one of the main results of the seminal paper by Bethe.⁸ Bethe found that in that situation, the hole can be described solely with an electric dipole moment perpendicular to the plane of the hole and a magnetic dipole moment lying in the plane of the hole, both of them scaling as d⁶. Due to the symmetry of our incoming field with J_z=1 we would be unable to induce an electric dipole moment with such orientation, leaving only the magnetic dipole moment. Since a field emitted by a magnetic dipole is an equal weight superposition of the two helicities, this model would predict a value of γ=1. The scaling of the total transmitted power, as well as of each of the helicity modes, would be d⁶. We did not probe very small holes of the order of λ/10 or below, but the trend of our smallest holes having large corresponding γ values is already evident in Figure 2. As we have shown, we observe a difference between the scaling of the two helicity components for larger holes within the range of hole sizes we probed experimentally. This change is due to the higher multipolar moments that start to play a role with increasing hole size.

Figure 4

Scaling of the different components of the transmitted beam. (a) contains experimental results, while (b) shows simulation results, which were obtained for a perfectly flat 200 nm thick gold layer. The unchanged helicity component (Λ=1, in black) has a faster scaling with the aperture diameter, d with d^3.75 and d^3.73 for the experimental and simulation values, respectively. The transformed helicity component (Λ=−1, in red) conversely shows a slower scaling with d^2.08 and d^2.17 for the experimental and simulation values.

While similar experimental set-ups and measurements have been previously reported,^22,23,24 in all these cases, the results have been analyzed by means of the spin (S) to orbital (L) angular momentum conversion mechanism. Yet, considering helicity (Λ) and total angular momentum (J) instead, bears significant advantages.^2,6 In particular, helicity Λ and the components of the angular momentum J can be connected with their corresponding symmetries: electromagnetic duality and rotations, respectively. In this paper, we have shown how to control the helicity of the light incident on the nanoaperture, and how to measure the helicity of the transmitted light, so that we are able to find the helicity conversion that occurs during the scattering process. This has allowed us to use the generator of generalized duality transformations, (Λ), along with the generator of rotations along the z axis, J_z, to analyze our experimental results from the point of view of symmetries and conserved quantities. Our framework has allowed us to identify the root cause of the relatively high helicity change by means of qualitative and quantitative considerations. We have found a difference in the scaling of the changed compared to the unchanged helicity with the aperture diameter. In the small aperture limit, we are able to predict a value of γ=100% where the scattered field is equally distributed between the two helicities. Furthermore, since helicity preservation is linked with duality symmetry, it is conceivable to tailor the helicity conversion in a nanophotonics experiment through the control of the effective duality of the scatterer, for example by employing metamaterials.

Conclusions

In this article, we have shown how to prepare, manipulate, and measure light with well defined helicity. This task requires only very simple optical elements and standard experimental procedures, but opens up new possibilities for analyzing light–matter interactions. In particular, the observables total angular momentum and helicity, linked with the corresponding symmetries rotational invariance and duality, are useful for the study of nanophotonics experiments that would usually be labeled as exhibiting conversion between spin and orbital angular momenta. Armed with this knowledge, we have experimentally investigated helicity transformations in focused light fields that interact with cylindrical nanoapertures in a gold film over a glass substrate. Analyzing the results by means of symmetries and conserved quantities, including duality and helicity, we have been able to conclude that the role of the nanoapertures is to allow light to couple to resonant modes of the system where duality is strongly broken: this is what renders the helicity transformation effect observable in our experimental set-up.