Introduction

Climate change is expected to alter carbon cycle feedbacks from soils through shifts in the composition and carbon accrual rates of plants and microbes, as well as the magnitude and sign of nutrient fluxes (Manzoni et al., 2008; Melillo et al., 2011; Zhou et al., 2012; Weedon et al., 2013). However, these feedbacks are not yet predictable because we lack both mechanistic understanding and appropriate model structure. Theoretical analyses have been developed to account for the roles of microbes and/or exoenzymes in decomposition of litter and soil organic matter (SOM; for example, Schimel and Weintraub, 2003; Lawrence et al., 2009; Allison et al., 2010; Davidson et al., 2012; Moorhead et al., 2012; Wang et al., 2013). Observations suggest that a critical parameter, the microbial carbon use efficiency (CUE) or microbial growth efficiency, is likely to decrease as a function of warming (Devevre and Horwath, 2000; Manzoni et al., 2008; Steinweg et al., 2008), which may result in lower microbial biomass, lower enzyme production and reduced heterotrophic respiration rates (Bradford et al., 2008; Hartley and Ineson, 2008; Tucker et al., 2013; Wang et al., 2013). These changes can occur either through physiological adjustments in individual microbial species/populations, for example, microbial CUE, or through shifts in the microbial community composition that change overall soil community CUE, or complex combinations thereof (Manzoni et al., 2012; Zhou et al., 2012). When the response of CUE to temperature change is not considered in models, soil carbon losses become magnified over time with warming (Frey et al., 2013; Wieder et al., 2013). When temperature-modified CUE is included, acclimation of the community to warmer temperatures moderates soil carbon loss (Sierra et al., 2010; Wieder et al., 2013), which is consistent with some experimental observations (Frey et al., 2008; Zhou et al., 2012). The ability to understand the activities of microbes in response to climate change and perturbations appears to be key to predicting carbon cycle–climate feedbacks.

Microbially controlled SOM decomposition is increasingly represented in ecosystem models (Treseder et al., 2012). Other vital common evolutionary traits, however, such as microbial dormancy and community shifts are not yet represented (Jones and Lennon, 2010; Weedon et al., 2013). When environmental conditions are unfavorable for growth, microbes may enter a state of low metabolic activity until conditions improve to allow replication (Stolpovsky et al., 2011; Wang et al., 2014b). Failure to consider dormancy in microbially controlled decomposition could result in underestimate of microbial biomass. Alternatively, measurements of microbial biomass such as chloroform fumigation and quantitative polymerase chain reaction cannot readily inform microbial models unless the extent of dormancy is considered (Wang et al., 2014b). Although soil respiration data are the most available and reliable observations for calibration and validation of models from point to global scale (Raich and Schlesinger, 1992; Hanson et al., 2000), estimates of microbial biomass, and even stoichiometry, will ultimately be needed to parameterize microbial ecosystem models (Sinsabaugh et al., 2013; Xu et al., 2013).

Microbial SOM decomposition models contain two major categories of parameters: decomposition parameters and microbial parameters. Microbial parameters are related to microbial growth and maintenance and include maximum specific growth and maintenance rates, true growth yield (YG) and the half-saturation constant for microbial uptake (Wang et al., 2014b). Our previous work has modified the microbial parameters using the physiological model to account for the extent of dormant versus active microbes (Wang et al., 2014b). Short-term (that is, several days) substrate-induced respiration and substrate-induced growth response experiments can be used to estimate many microbial parameters (Van de Werf and Verstraete, 1987; Colores et al., 1996; Blagodatskaya and Kuzyakov, 2013). However, the short-term nature of these experiments means that decomposition parameters for many slowly decomposing substrates cannot be estimated from them (Wang et al., 2014b). Decomposition parameters refer to the kinetic parameters directly controlling decomposition rates, for example, rate constants in first-order kinetic models (Lawrence et al., 2009), enzyme kinetics (maximum specific enzyme activity and corresponding half-saturation constant), and enzyme production and turnover rates (Schimel and Weintraub, 2003; Tang and Riley, 2013; Wang et al., 2013).

In this study, we incorporated the dormant and active microbial physiological model developed in Wang et al. (2014b) into the microbial enzyme-mediated decomposition (MEND) model that represents the microbial enzyme-driven biological processes as well as the mineral-associated physicochemical processes (Wang et al., 2013). Carbon isotopes were also represented in MEND to distinguish fluxes of native SOM from added 14C-labeled substrates, thus providing additional data for model parameterization (Hanson et al., 2005; Thiet et al., 2006; Parton et al., 2010). We tested two versions of MEND, that is, MEND with dormancy (hereinafter referred to as MEND) and MEND without dormancy (hereinafter referred to as MEND_wod), against C decomposition data collected from long-term laboratory incubations of soils with isotopically labeled substrate additions. We hypothesized that (i) MEND would be superior to MEND_wod to more accurately estimate microbial and SOM dynamics; (ii) long-term (∼1 year) soil incubation experiments with observations of diverse response variables (for example, respiration, microbial biomass, dissolved organic carbon (DOC) and C isotopes) are useful for estimating decomposition parameters in addition to microbial parameters.

Materials and methods

MEND model accounting for microbial dormancy

We divided the microbial biomass pool in original MEND (MEND_wod) into two fractions, that is, active and dormant microbial biomass (BA and BD; Figure 1 for model diagram). The microbial physiology component was incorporated into MEND to account for the transition of microbes between the two physiological states (active and dormant; Wang et al., 2014b). The particulate organic carbon (POC) pool may be divided into several sub-pools representing different substrate categories. For example, as per our laboratory experiments with addition of glucose and starch, we divided the POC pool into two components: POC1 (denoted by P1) containing lignocellulose-like compounds and POC2 (denoted by P2) including starch-like compounds. P1 is degraded by ligninases and cellulases (Wang et al., 2012; Li et al., 2013), and P2 is broken down by amylases (Caldwell, 2005; Swarbreck et al., 2011). The DOC (D) pool contains compounds of varying complexity that can be bound to active layer of mineral-associated organic carbon (MOC, M) pool, that is, the Q pool in Figure 1 (Mayes et al., 2012; Wang et al., 2013). In MEND, the DOC (D) pool receives inputs from decomposition of POC (P) and MOC (M), desorption of C from Q, and dead enzymes and microbes (microbial biomass carbon, MBC).

Figure 1
figure 1

Diagram of the microbial ezyme-mediated decomposition (MEND) model. Soil organic carbon pools include: particulate organic carbon (POC) (for example, lignocellulose-like compounds and starch-like compounds, denoted by P1 and P2, respectively), mineral-associated organic carbon (MOC, denoted by M), dissolved organic carbon (DOC, D), adsorbed phase of DOC (QOC, Q), active microbial biomass (BA), dormant microbial biomass (BD), POC-degraded enzymes (for example, EP1 and EP2 that break down P1 and P2, respectively), and MOC-degraded enzymes (EM). IP1, IP2 and ID are external inputs to the pools of P1, P2, and D, respectively. Transformation fluxes include: (1) POC1 (P1) decomposition (denoted by the flux F1 in equations in the Supplementary Information); (2) POC2 (P2) decomposition (F2); (3) MOC (M) decomposition (F3); (4, 5) adsorption (F4) and desorption (F5) between DOC (D) and QOC (Q); (6) DOC (D) uptake by BA (F6); (7,8) dormancy (F7) and reactivation (F8) between BA and BD; (9, 10) BA growth respiration (F9) and maintenance respiration (F10); (11) BD maintenance respiration (F11); (12) BA mortality (F12); (13) synthesis of EP1 (F13,EP1), EP2 (F13,EP2), and EM (F13,EM); and (14) turnover of enzymes (F14,EP1, F14,EP2, and F14,EM).

Full size image

The dynamics of each soil C pool in MEND is described by Supplementary Equations S1–S12 in the Supplementary Information. The transformation fluxes (Figure 1) are elucidated by Supplementary Equations S13–S26 in Supplementary Table S1 in the Supplementary Information. Model parameters and their a priori value ranges adapted from Wang et al. (2013) are summarized in Table 1.

Table 1 MEND model parameters
Full size table

There are two additional parameters for model initialization: initial active fraction (r0) and initial lignocellulose fraction (LCF0; Table 1). r0 is the initial fraction of active microbes within total living microbes (Wang et al., 2014b). LCF0 is defined as the initial ratio of particulate lignocellulose–carbon (P1) concentration to the total POC concentration. We define an index α=mR/(VD+mR), where VD and mR denote maximum specific growth and maintenance rates, respectively, for active microbes. Either mR or α is included in model calibration, as one of them can be derived from the other. Similarly, the binding affinity (KBA) and desorption rate (Kdes) are calibrated, and the specific adsorption rate (Kads=Kdes × KBA) can be computed from them. In MEND, the ratio of dormant to active maintenance rate is set to a constant (that is, β=0.001), as the model is not sensitive to β during the experimental period (for example, within 1 year; Wang et al., 2014b). Compared with MEND_wod, there is one more parameter in MEND—the initial active fraction (r0). In summary, there are 20 parameters for calibrating MEND and 19 for MEND_wod.

Discriminating isotopes in the MEND model

The MEND and MEND_wod models were also modified to explicitly account for different C isotopes (for example, 12C, 13C and 14C), that is, the soil C pools and fluxes represented in Figure 1 were duplicated to consider different C isotopes. General assumptions for the isotopically explicit MEND models include: (i) isotopic fractionation in SOM transformation, microbial processing and respiration is negligible (Sala et al., 2000; Currie, 2007); (ii) each pool is mixed well and isotopically homogeneous, and influxes to a pool can alter its isotopic ratio, whereas outfluxes from a pool cannot (Currie, 2007). In this study, two C isotopes (14C and 12C) were included, and the flux of 14C or 12C is assumed to depend on the isotopic ratio (14C/12C) in the upstream pool.

where and represent the 14C and 12C flux, respectively; FC is the total C flux; and Rup=(14C/12C)up denotes the isotopic ratio (14C/12C) in the upstream pool.

Model parameter optimization

We used the SCEUA (Shuffled Complex Evolution at University of Arizona) algorithm (Duan et al., 1992; Wang et al., 2009) to determine model parameters. We implemented SCEUA with 30 different random seeds (Duan et al., 1992). The parameter optimization is to minimize the total objective function (J) that is computed as the weighted average of multiple single-objectives (Wang and Chen, 2012)

where m denotes the number of objectives and wi is the weighting factor for the ith (i=1, 2,…, m) objective (Ji).

In this study, the total objective function (J) consists of four single-objectives (that is, m=4) in terms of four response variables: J1 for total cumulative respiration (denoted by C–CO2), J2 for cumulative respired 14C normalized by added 14C (denoted by %14C–CO2), J3 for MBC and J4 for DOC. The computation of each single-objective includes the data from two experiments (with addition of glucose and starch). For example, we merged the respiration data with glucose addition (number of data points n=14) and the respiration data from starch (n=14) into one data set (n=28) for computing J1.

The objectives J1 (for C–CO2) and J2 (for %14C–CO2) were computed as (1−R2), where R2 denotes the coefficient of determination (Devore, 2008), and higher R2-values (R2 ⩽1) indicate better model performance; while the objectives J3 and J4 (for MBC and DOC, respectively) were calculated by the mean absolute relative error (MARE) and lower MARE values (MARE ⩾0) are preferred (Dawson et al., 2007). We used a different formulation for J1 and J2 from J3 and J4 because we had more observations for C–CO2 and %14C–CO2 (n=28 with glucose and starch for each of them) than for MBC and DOC (n=8 for each of them). R2 is not suitable for assessing the goodness-of-fit regarding a small amount of data. MARE represents the averaged deviations of predictions (Ysim) from their observations (Yobs):

Uncertainty and statistical analyses

The uncertainties in parameters and model predictions were quantified by the Critical Objective Function Index (COFI) method, which is much simpler than the commonly used method based on Bayesian inference and Markov Chain Monte Carlo (Wang and Chen, 2013). The COFI method is based on a global stochastic optimization technique (for example, SCEUA in this study). It also accounts for model complexity (represented by the number of model parameters) and observational data availability (represented by the number of observations).

The procedure of COFI includes: (i) implementing the SCEUA algorithm with multiple different random seeds to search ‘relatively optimal’ parameter sets that minimizing the objective function (J in Equation (2)); (ii) collecting the optimal parameter set generated in each loop of the SCEUA searching process to form a feasible parameter space; (iii) determining the COFI (Jcr; see Equation (4) below) based on Jopt (minimum J-value), n (number of measurements) and p (number of model parameters); (iv) constructing the parametric surface of the confidence space by selecting those parameter sets resulting in J⩽Jcr from the feasible parameter space; (v) quantifying the uncertainty in parameters by the statistics of these selected parameter sets; (vi) conducting model simulations using these selected parameter sets; and (vii) quantifying the uncertainty in model predictions (for example, soil C pool sizes and respiration) using the model simulation outputs.

The COFI is computed as (Batstone et al., 2003; Wang et al., 2014a):

where Jcr is the COFI that defines the parameter uncertainty region, Jopt is the optimum (minimum) objective function value that is calculated by Equation (2a), n is the number of measured data points, p is the number of parameters, and Fα,p,n−p is the value of the F-distribution for α, p and n−p. For MEND, P=20, n=72 (including measured C–CO2, %14C–CO2, DOC and MBC in two experiments with addition of glucose and starch), we used α=0.05, with F0.05,20,52=1.776 to estimate the 95% confidence parameter uncertainty regions. For MEND_wod, P=19 (that is, r0 is not included) and F0.05,19,53=1.786. As a result, η=1.683 and 1.640 for MEND and MEND_wod, respectively. It is evident that more observed data points and less undetermined parameters would reduce parametric uncertainty (that is, smaller Jcr).

We used the non-parametric Kruskal–Wallis analysis of variance to test whether the parameter samples for each soil originated from the same distribution at a significance level of 0.05 (McDonald, 2009; Giraudoux, 2013).

Soils and incubation experiments

We have chosen to study four soils selected from contrasting climatic zones, the experimental details of which were published previously: A Gelisol from arctic, Andisol from sub-arctic, Mollisol from temperate, as well as an Ultisol from tropical regions (Jagadamma et al., 2014a, 2014b). In brief, each soil was incubated at room temperature (20 °C) for 270 days in the dark in a temperature and humidity controlled room. For each sample, 25 g soil were pre-incubated at 40% water holding capacity for 1 week to avoid the respiration response of the microbial community to rewetting (Paul et al., 2001; Haddix et al., 2011). Each soil sample was amended with unlabeled substrate (D-glucose or starch) at the concentration of 0.4 mg C g−1 soil and with uniformly labeled 14C substrates (U-14C glucose or U-14C starch). The added glucose and starch were assumed to enter the DOC (D) and POC_starch (P2) pool, respectively. The initial conditions of soils are summarized in Table 2. The initial Q pool size was assumed to be 1% of the MOC (M) pool size and the initial enzyme concentrations for EP1, EP2 and EM were set to 1.1 × 10−3, 1.1 × 10−3 and 1.4 × 10−3 mg C g−1 soil, respectively (Wang et al., 2013). The radiocarbon labeled glucose and starch were added to soils that had isotopic ratios (R=14C/12C) of 4.80 × 10−6 (for glucose) and 4.68 × 10−6 (for starch), respectively. Cumulative total respiration (denoted by C–CO2 in units of mg C g−1 soil) and cumulative respired 14C normalized by added 14C (denoted by %14C–CO2) were measured 14 times in three replicates, that is, at days of 1, 2, 4, 6, 10, 15, 30, 45, 60, 90, 120, 150, 210 and 270. In addition, MBC and DOC were determined at 4 days, that is, 4, 30, 150 and 270. Additional details about the soils and the laboratory-incubation experiments can be found in Jagadamma et al. (2014a, 2014b).

Table 2 Experimental soils and their initial soil carbon pool sizes (mg C g−1 soil)
Full size table

Results

Model simulations

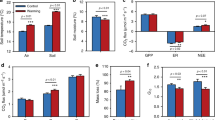
Both MEND and MEND_wod could simulate the observed C–CO2, %14C–CO2 and DOC with similarly satisfactory criterion values (Figures 2a, b and d). Higher R2-values (R2 ⩽1) indicate better model performance, whereas lower MARE values (MARE ⩾0) are preferred. The R2-values for C–CO2 and %14C–CO2 are >0.85 and close to the ideal R2-value (1.0). The MARE values for DOC are <0.32 with most of them <0.20 for both models. For MBC, the MARE values for MEND_wod are >0.65 and are 25–126% higher than those for MEND (Figure 2c). MEND_wod underestimated 91% of the 32 MBC observations (eight observations for each of the four soils), whereas the MEND underestimated 75%. When dormancy was not considered, the MARE for MBC predictions averaged out to 0.70 during the full experimental period and 0.95 during the latter period (at days of 150 and 270). When dormancy was included, the average MARE values were reduced to 0.37 and 0.47 for the full period and the latter period, respectively. Thus, MEND improved model estimates of MBC concentrations by 20–71% over MEND_wod across four soils.

Figure 2
figure 2

Best criterion values for calibrating MEND model with dormancy (MEND) or without dormancy (MEND_wod). (a) R2 for C–CO2 (cumulative C–CO2 respiration); (b) R2 for 14C–CO2 (normalized cumulative 14C–CO2 by added 14C); (c) MARE for MBC (microbial biomass carbon); (d) MARE for DOC (dissolved organic carbon). R2: coefficient of determination, higher R2-values (R2 ⩽1) indicate better model performance; MARE, mean absolute relative error (Equation (3)), lower MARE values (MARE ⩾0) are better.

Full size image

Taking the Mollisol as an example (Figure 3, the error bars for model simulations were derived by the COFI method), the simulated C–CO2 (Figures 3a and c), %14C–CO2 (Figures 3b and d) and DOC (Figures 3f and h) by both models fit the observations very well. MEND_wod greatly underestimated %14C–CO2 during the first 2 days (see the left two points in Figures 3b and d) and slightly underestimated %14C–CO2 from days 2 to 15 (data point 3–6 in Figures 3b and d). However, MEND improved the estimates of %14C–CO2 for the same period. The simulated MBC concentrations (Figures 3e and g) by MEND were also close to the observations, while MEND_wod significantly underestimated MBC at days 150 and 270. Similar results were found for the other soils (see Supplementary Figure S1 in the Supplementary Information).

Figure 3
figure 3

Comparison between observations (Obs) and simulations (Sim) for the Mollisol, where ‘MEND’ and ‘MEND_wod’ denote the MEND model with and without dormancy, respectively. (a) C–CO2 (cumulative C–CO2 respiration) with addition of glucose. (b) %14C–CO2 (normalized cumulative respired 14C by added 14C) with glucose. (c) C–CO2 with addition of starch. (d) %14C–CO2 with starch. (e) MBC (microbial biomass carbon) with glucose. (f) DOC (dissolved organic carbon) with glucose. (g) MBC with starch; (h) DOC with starch. The horizontal error bars in a–d are s.d. for observations (sample size n=3) at days of 1, 2, 4, 6, 10, 15, 30, 45, 60, 90, 120, 150, 210 and 270 (from left to right); the vertical error bars in a–d are s.d. for C–CO2 simulated by MEND (n=2346); for clarity, the error bars (similar to MEND) by MEND_wod are not shown in a–d. No error bars are shown for observations in e–h because of the lack of replicate measurements. The error bars in e–h are s.d. for simulations; for clarity, only the positive errors are shown.

Full size image

Model parameters

The parameter analysis in this section is focused on MEND, as it represents microbial dynamics better and presents superior model performance than MEND_wod. The boxplots for model parameters derived by the COFI method are shown in Supplementary Figure S2 in the Supplementary Information. In most cases, the calibrated parameter values varied among soils. The Andisol held the highest values in seven parameters (rE, VP2, KP1, KM, Qmax, KD and gD) and the lowest in the other seven parameters (mR, VD, pEM, VP1, VM, KP2, Kdes).

The decomposition parameters varied in different SOC pools (Supplementary Figure S2). The MOC (M) pool had the lowest maximum specific decomposition rate (median of VM=0.93, 95% confidence interval (CI)=0.06–1.98 mg C mg−1 C h−1) and the largest half-saturation constant (median of KM=550, 95% CI=35–998 mg C g−1 soil). The P2 pool (starch) held the highest specific decomposition rate (median of VP2=42, 95% CI=16–50 mg C mg−1 C h−1) and the lowest half-saturation constant (median of KP2=6, 95% CI=1–56 mg C g−1 soil). The P1 (lignocellulose) had slightly higher specific decomposition rate (median of VP1=1.17 mg C mg−1 C h−1) than the M pool while having a modest half-saturation constant (median of KP1=58 mg C g−1 soil). Other decomposition parameters are related to the turnover and production of enzymes (rE, pEP and pEM). The overall rE (enzyme turnover rate) had a median of 0.003 with the 95% CI the same as the a priori (0.0001–0.01). The Gelisol exhibited the lowest median rE (0.001). The distributions of rE were not statistically different between the Mollisol and the Andisol (median=0.004 and 0.005, respectively). The median rE for the Ultisol (0.002) was between the previous two groups (Supplementary Figure S2). The fractions of mR for the production of EP and EM (pEP and pEM) across four soils had medians of 0.06 and 0.04, respectively, with their 95% CIs almost identical to their a priori ranges.

Major microbial parameters in MEND include the specific maintenance and growth rates (mR and VD), the half-saturation constant for microbial uptake (KD) and the YG. The medians of mR and VD for the four soils were 0.01 and 0.03 mg C mg−1 C h−1, respectively, (Supplementary Figure S2). mR and VD were significantly different among the four soils with the highest in the Gelisol and the lowest in the Andisol. KD exhibited a median of 0.467 (95% CI=0.09–0.50 mg C g−1 soil). The overall YG had a median of 0.43 with 95% CI of 0.10–0.75 (Supplementary Figure S2). The medians (close to the means) for the Gelisol, Andisol, Mollisol and Ultisol were 0.25, 0.42, 0.49 and 0.52, respectively.

Discussion

Model parameterization

The Andisol stands out of the four soils in terms of model parameters because Andisols are different from other soil pertaining to their physical, chemical and mineralogical properties (Nanzyo, 2002; McDaniel and Wilson, 2007). The Andisol contained significantly higher SOC than the other soils (Table 2) but generally produced lower cumulative C–CO2 than the Mollisol and Ultisol during the experimental period. Thus the model calibration required the lowest specific reaction rates (for example, mR, VD, VP1 and VM) and the highest half-saturation constants (for example, KP1, KM and KD) for the Andisol. The median values for mR and VD derived here are two orders of magnitude higher than those in Wang et al. (2013). This is because of the consideration of microbial dormancy. The MEND_wod model and other microbial models include only one microbial biomass pool and do not consider the physiological states of microbes. Thus, the mR values in Wang et al. (2013) were summarized from literature including maintenance rates for active microbes (Anderson and Domsch, 1985b) or dormant microbes (Anderson and Domsch, 1985a) or the total microbial biomass. In MEND, mR solely refers to the maximum specific maintenance rate of active microbes. The large differences in mR and VD between MEND and MEND_wod point to the importance of proper accounting in parameterization of microbial ecosystem models.

Our results showed the dependence of YG on the changes in temperature (ΔT in Figure 4), where ΔT is the difference between incubation temperature (20 °C) and the mean annual temperature (Table 2). Figure 4 shows that YG decreased with increasing ΔT from 0.7 to 22.9 °C. The temperature-response coefficient for YG (that is, the regression slope in Figure 4) was approximately −0.01 °C−1 with 95% CI of (−0.016 and −0.005) °C−1, which comprises previous experimental estimates (Devevre and Horwath, 2000; Steinweg et al., 2008; Tucker et al., 2013). This dependence of YG on ΔT (Figure 4) may imply that microbes have been acclimated to their local environments and exhibit a relatively universal YG (averaged 0.56 with 95% CI of 0.48–0.64) across different biomes.

Figure 4
figure 4

Dependence of true growth yield (YG) on changes in temperature. MAT, mean annual temperature at the soil sampling site; CI, confidence interval; LCL, and UCL are lower and upper confidence limits, respectively. The YG-values for each soil (from left to right: Ultisol, Mollisol, Andisol and Gelisol) are 13 representative values corresponding to 13 percentiles (2.5, 5, 10, 20, 30, 40, 50, 60, 70, 80, 90, 95 and 97.5%).

Full size image

When observations are available for various response variables, the strategy of multi-objective calibration is essential in order to reduce uncertainty in model parameterization (Yapo et al., 1998; Wang and Chen, 2012). We conducted model parameterization aiming at minimizing a synthesized objective function that consists of four objectives in terms of C–CO2, %14C–CO2, DOC and MBC. The optimal parameter sets reflected a balance among all objectives. We also found that the parameterization results could be qualitatively different when a new objective was introduced into the calibration process. Our previous study indicated that short-term substrate-induced respiration or substrate-induced growth response experiments could be used to determine microbial parameters (Wang et al., 2014b). This study further shows that the long-term (that is, ∼1 year) soil incubations or field experiments with measurements of microbial biomass in addition to soil respiration are conducive to estimate decomposition parameters in addition to microbial parameters. We also advocate the incorporation of isotopic signatures into parameterization and evaluation of ecosystem models. We have shown our efforts in parameterizing the model in terms of diverse soils from different climatic regions. We hope that these parameter values could provide documented references, although with large uncertainty, for relating parameters to soil properties and/or climatic conditions. Nevertheless, more laboratory- and field-scale data sets are needed to constrain model parameterization and associated uncertainty. By this way, the microbial mechanisms could be practically incorporated into ecosystem models to represent microbial-controlled processes.

Microbial dormancy

The observations of low respiration rates but modest MBC and DOC concentrations during the latter period (for example, after 50 days) of incubation imply there must be certain mechanisms further depressing microbial activities. The total MBC or DOC usually exhibited a decreasing trend after 4 days, but MBC concentrations at day 150 were as high as 28–89% of initial MBC, and DOC concentrations were at least 30% of initial DOC. The lower microbial activities are reflected by the slower increase in cumulative C–CO2 and 14C–CO2 (Figures 3a–d). That is why very low MBC concentrations (compared with initial MBC) were predicted with satisfactory predictions of DOC when MEND_wod was adopted (Figures 3e and g, and Supplementary Figure S1). Major factors affecting microbial activities include environmental factors (for example, soil temperature and moisture; Brockett et al., 2012), carbon availability or root exudation (Drake et al., 2013) and nutrient availability (Lennon and Jones, 2011). Changes in these factors might result in changes in CUE (Sinsabaugh et al., 2013) and transitions between microbial physiological states (active and dormant), particularly in laboratory-scale experiments. For example, dormancy is a beneficial survival and evolutionary trait of soil microbes when faced with unfavorable environmental conditions (Lennon and Jones, 2011). The impacts of environmental factors and root exudation could be excluded from this study, as the soils without living roots were incubated at an aerobic environment with constant soil temperature and moisture. We found that the prediction of microbial biomass could not be improved by simply manipulating the intrinsic CUE (that is, YG) in MEND_wod. Thus, the transition between microbial physiological states owing to changes in carbon or nutrient availability is the most likely explanation for the observed variations in microbial activities.

The MEND model substantially improved the predictions of microbial biomass over MEND_wod, indicating that it is essential to represent dormancy in microbial ecosystem models in order to accurately predict microbial biomass as well as to explain variation in SOM decomposition as a function of time. The initial active fractions (r0) in this study averaged 0.79 (median=0.90) with large variations (95% CI=0.19–0.99). The relatively high r0 might be due to the pre-incubation of soil samples at 40% water holding capacity for 1 week. The active fraction (r) generally declined with time due to the decrease in substrate (DOC) availability. Taking the Mollisol as an example, the active fraction (r) dropped from its initial value of 0.655 to 0.104 after 50 days (Figure 5). At day 150, the predicted MBC concentrations by MEND_wod only accounted for 3–8% of the initial MBC across four soils, which were much lower than the observations (>28% of initial MBC). The incorporation of dormancy was able to resolve the large discrepancies in total MBC between model predictions and experimental observations.

Figure 5
figure 5

Temporal change in active fraction (r) of microbial biomass for the Mollisol.

Full size image

MEND_wod could adequately fit the other observations (C–CO2, %14C–CO2 and DOC), but at the cost of significantly underestimating the total microbial biomass. In other words, if the total microbial biomass could be more satisfactorily modeled, the model without dormancy would poorly simulate soil respiration, not to mention that microbial uptake and respiration are more sensitive to the changes in MBC than to the changes in DOC concentration regarding the Michaelis–Menten kinetics (Wang and Post, 2013). Taking the Mollisol as an example, when MBC was given greater weight in the objective function (Equation (2)) of MEND_wod, the best MARE for MBC could be improved from 0.66 (when soil respiration was given greater weight) to 0.27; however, the model was not good at simulating C–CO2 (best R2=0.78) compared with the model performance shown in Figure 2 (best R2=0.98 for C–CO2). In this MEND_wod configuration, the cumulative respiration at day 270 was overestimated by 29%, compared with the relative small errors of 5% from MEND. In conclusion, the inclusion of dormancy substantially improves the estimates of microbial biomass as well as the mechanistic representation and prediction of soil carbon cycle.

Feedbacks between the climate system and the carbon cycle is a major focus of global change research (Zhou et al., 2012). Biogeochemical cycles including the carbon cycle are extensively driven by microbes (Falkowski et al., 2008). The two necessary conditions for soil microbes to affect ecological processes are: (a) ‘organisms must differ in their functional traits’ and (b) ‘biological reactions must be either the rate-limiting step or the fate-controlling step’ (Schimel and Schaeffer, 2012). Microbial functional groups are characterized by certain functional traits, such as life-history traits and substrate-specificity traits (Kaiser et al., 2014). The newly developed microbial mineral carbon stabilization model defines two microbial functional groups (r- and K-strategies) that differ in growth rate, turnover rate and their interactions with physically and chemically protected SOM pools (Wieder et al., 2014). Our model testing against experimental data demonstrates that the microbial control over SOM decomposition is substantial. In addition, active and dormant microbes distinctly differ in their functional traits, and the extent of microbial decomposition and uptake is the rate-limiting step.

The dormancy strategy should be more significant for microbes in field conditions that are influenced by carbon and nutrient availability and changes in environmental factors such as soil temperature, moisture and oxygen (Wang et al., 2014b). For example, dormancy has been found to be a better strategy to achieve drought resistance in mineral soils where C supply constrains growth and osmolyte synthesis (Manzoni et al., 2014). The proposed dormancy mechanism and calibrated microbial, and enzymatic parameters with long-term laboratory incubations provide a pathway forward for modeling field-scale processes. Although the importance of microbial community composition may vary with spatiotemporal scales (Schimel and Schaeffer, 2012), the inclusion of microbial physiology is essential to confidently project feedbacks between climate change and carbon cycle (Bradford, 2013). Continued development is needed to bring microbial physiology into global climate and ecosystem models (Todd-Brown et al., 2012; Treseder et al., 2012; Schimel, 2013).