Abstract
The processes and timescales associated with ocean-wide changes in the distribution of marine species have intrigued biologists since Darwin’s earliest insights into biogeography. The Azores, a mid-Atlantic volcanic archipelago located >1000 km off the European continental shelf, offers ideal opportunities to investigate phylogeographic colonisation scenarios. The benthopelagic sparid fish known as the common two-banded seabream (Diplodus vulgaris) is now relatively common along the coastline of the Azores archipelago, but was virtually absent before the 1990s. We employed a multiple genetic marker approach to test whether the successful establishment of the Azorean population derives from a recent colonisation from western continental/island populations or from the demographic explosion of an ancient relict population. Results from nuclear and mtDNA sequences show that all Atlantic and Mediterranean populations belong to the same phylogroup, though microsatellite data indicate significant genetic divergence between the Azorean sample and all other locations, as well as among Macaronesian, western Iberian and Mediterranean regions. The results from Approximate Bayesian Computation indicate that D. vulgaris has likely inhabited the Azores for ∼40 (95% confidence interval (CI): 5.5–83.6) to 52 (95% CI: 6.32–89.0) generations, corresponding to roughly 80–150 years, suggesting near-contemporary colonisation, followed by a more recent demographic expansion that could have been facilitated by changing climate conditions. Moreover, the lack of previous records of this species over the past century, together with the absence of lineage separation and the presence of relatively few private alleles, do not exclude the possibility of an even more recent colonisation event.
Similar content being viewed by others
Introduction
Patterns of population connectivity in marine fish depend not only on their dispersal abilities and historical demography, both of which are influenced by the proximity of putative source populations, but also on a complex interplay of these characteristics with environmental factors, such as habitat fragmentation, oceanic currents and climatic fluctuation (Chopelet et al., 2009). Patterns of genetic structure are, therefore, best understood through the integration of ecological, spatial, environmental and historical information.
The archipelago of the Azores has long represented an attractive target for phylogeographic studies of littoral fishes: the volcanic origin and continued dynamism of these islands, in combination with their remote location, provide an ideal system to investigate the colonisation history of insular species, and pinpoint the traits favourable to their dispersal, establishment and expansion. The majority of studies report genetic isolation in Azorean fishes, because of limited gene flow with the neighbouring island of Madeira, as is the case of the shanny, Lipophrys pholis (Stefanni et al., 2006) and the Montagu’s blenny, Coryphoblennius galerita (Domingues et al., 2007a; Francisco et al., 2014). Studies on other species in the Azores, for example, the ornate wrasse Thalassoma pavo (Costagliola et al., 2004) and the white seabream Diplodus sargus (Domingues et al., 2007b), report low genetic diversity, most probably attributable to the peripheral position of these populations.
The common two-banded seabream, Diplodus vulgaris (Geoffroy Saint-Hilaire, 1817; Family Sparidae), is an interesting candidate for a phylogeographic study involving the Azores, as its occurrence has only been reported within the past 20 years. Before that, the only Diplodus species known to inhabit Azorean coastal waters was the white seabream, D. sargus (Santos and Nash, 1995). D. vulgaris is a benthopelagic fish occurring in rocky and sandy bottoms between the Bay of Biscay, Senegal and the Canary Islands, including the Mediterranean and the Black Sea. Its bathymetric range extends from the shallow subtidal zone down to the depth of ∼90 m (Whitehead et al., 1986). The distribution area of D. vulgaris shows a large degree of overlap with the congeneric species D. sargus (Linnaeus, 1758), in which they coexist in relatively segregated niches (Mariani et al., 2002).
A detailed checklist of the ichthyofauna of the Azores (Santos et al., 1997) does not include records of D. vulgaris, although there is mention of its presence in the nineteenth century (Hilgendorf, 1888). Informal interviews with fishermen and local divers suggest that this species was not known in these islands before the late 1990s (S Stefanni, personal communication). D. vulgaris does not have a common/vernacular name in the Azores and the nineteenth century records were probably because of misidentification or misnaming (Santos et al., 1997). The authors of the present study were able to empirically follow the demographic increase of D. vulgaris, with individuals becoming more abundant in successive years, starting with the first recorded occurrence of early life stages in 1997 (Afonso et al., 2013) followed by the progressive establishment of all age classes from juveniles to large adults in the following years.
In the present study we test two different scenarios to explain the presence of D. vulgaris in the Azores: (1) a recent colonisation resulting from dispersal events and (2) the existence of an ancient relic population that remained undetected until a recent expansion over the past 20 years. With the first scenario, we hypothesise that the population from the Azores has settled as a result of one or more relatively recent waves of colonisers. The apparent absence of this species in the Azores before such events could be explained by the generally unfavourable directions of surface currents that might have prevented dispersal to the Azores. Under this scenario we would expect (1) the Azores population to display a demographic imprint of a recent genetic bottleneck and (2) modest genetic diversity of mitochondrial and nuclear markers, with haplotypes and microsatellites alleles representing a small subset of the main phylogroup of origin (for example, founder effect). Under the second scenario, the expectations are: (1) the old established Azores population to display stronger genetic divergence as a result of long-term isolation, (2) the accumulation of new mutations leading to higher levels of genetic diversity and (3) larger frequencies of private alleles and haplotypes in the refugial population. On the other hand, low genetic diversity may also be expected if the size of the relict population was very small, and this would lead to even more pronounced divergence and lineage sorting, as a result of genetic drift. To test these hypotheses, we compared samples from 11 locations in the NE Atlantic and Mediterranean using mitochondrial DNA (mtDNA; control region), one coding nuclear gene (first intron of the S7 ribosomal protein) and nine neutral microsatellites.
Materials and methods
Sampling and laboratory procedures
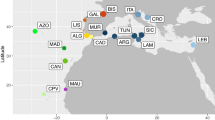
A total of 307 individuals of D. vulgaris were collected from 11 locations in the Mediterranean Sea and the NE Atlantic (mainland coast and islands) (Figure 1 and Table 1). Specimens from the Azores were collected by spearfishing at different sites around the island of Fayal during the years 2007 and 2008, fish from the Balearics were purchased directly from local fishermen in Palma de Mallorca in 2007, and all other tissue samples came from finclips donated by either fishermen or scientists, as part of collaborative projects between 2007 (Italy), 2008 (Canaries, Mauritania, central and southern Portugal, Cadiz and Malta) and 2009 (Madeira). All samples were stored in 96% ethanol until DNA isolation. This was conducted using commercial kits and following the manufacturers’ instructions: REDExtract-N-Amp kit (Sigma-Aldrich, St Louis, MO, USA) or Mag-Bind Tissue DNA Kit (Omega Biotek, Norcross, GA, USA). Voucher specimens (ethanol preserved tissues or finclips) have been deposited in the Institute for Marine Research/Department of Oceanography and Fisheries of the University of the Azores, Portugal (IMAR/DOP) and Superior Institute of Applied Psychology - Research Unit, Portugal (ISPA-IU) collections.
The 5' domain of the mitochondrial control region (CR) was successfully amplified and sequenced from 227 specimens for a portion of 344–345 bp in length (Genbank accession numbers: HQ997776–HQ997840 and JQ655470–JQ655598). The first intron of the S7 ribosomal protein gene (S7) was amplified and sequenced for 137 specimens for a portion of 269–271 bp in length (Genbank accession numbers: HQ997841–HQ997893 and JQ624680–JQ624764). Nine polymorphic microsatellites were also screened in all 307 specimens. The loci used were Dvul4, Dvul33, Dvul84 (Roques et al., 2007b), Omel2, Omel27, Omel38, Omel54, Omel58 (Roques et al., 2007a) and SL26 (Chopelet et al., 2009).
PCR amplifications of mtDNA CR and nuclear DNA S7 were performed independently with the following pairs of primers: LPro1 (5′-ACTCTCACCCCTAGCTCCCAAAG-3′) and HDL1 (5′-CCTGAAGTAGGAACCAGATGCCAG-3′) (Ostellari et al., 1996) for the mtDNA control region and S7RPEX1F (5′-TGG CCTCTTCCTTGGCCGTC-3′) and S7RPEX2R (5′-AACTCGTCTGGCTTTTCGCC-3′) (Chow and Hazama, 1998) for the S7 nuclear intron. PCR amplification reactions were performed in a 20 μl total volume with 10 μl of REDExtract-N-ampl PCR reaction mix (Sigma-Aldrich), 0.8 μl of each primer (10 μM), 4.4 μl of Sigma water and 4 μl of template DNA. An initial denaturation at 94 °C for 7 min was followed by 35/30 amplification cycles (denaturation at 94 º C for 30/45 s, annealing at 55 °C for 30/45 s and extension at 72 °C for 1 min) and a final extension at 72 °C for 7 min on a Bio-Rad (Hercules, CA, USA) Mycycler thermal cycler (values CR/S7, respectively). The same set of primers was used for sequencing that was carried out at the BMR Genomics (Padua, Italy) facility.
PCR amplification for the nine polymorphic microsatellites was performed in two multiplex reactions: one included Dvul33, Omel2, Omel27, Omel38, Omel54 and Dvul84, and the second reaction pooled Omel58, Dvul4 and SL26. The volume of reagents in the first multiplex reaction were 0.2 μl of each primer, 5 μl of master mix buffer, 0.8 μl of water and 2 μl of 25 ng μl−1 DNA. Volumes of reagents in the second reaction were: 0.2 μl of Omel58 primer, 0.25 μl of each Dvul4 and SL26 primer, 5 μl of master mix buffer, 1.2 μl of water and 2 μl of 25 ng μl−1 DNA. Reaction conditions for both multiplexes were as follows: 15 min at 95 ºC; 34 cycles at 94 °C for 45 s, 58 °C for 45 s, 72 °C for 45 s; and 72 °C for 45 min.
Genotyping was performed by allele sizing on an ABI 3130xl Genetic Analyser (Applied Biosystems) using forward primers labelled with NED, PET, FAM and VIC dyes, and an internal size standard labelled with LIZ 600 (Applied Biosystems, Foster City, CA, USA). The software GENEMAPPER version 4x (Applied Biosystems) was used to score alleles.
Data analysis
Sequences, including D. sargus (CR: EF468585; S7: EF467745) as outgroup, were aligned using Clustal X (Thompson et al., 1997) and CLC Main Workbench (CLC Bio, Aarhus, Denmark).
Genetic diversity indices for CR and S7 markers were estimated using the software ARLEQUIN 3.5 (Excoffier and Lischer, 2010). In S7, which has a biparental mode of inheritance, most individuals showed heterozygosity, and therefore we used the ELB algorithm (Excoffier et al., 2003) to phase alleles. Nucleotide diversity (π) and haplotype diversity (h) were calculated independently for CR and S7 sequences.
Phylogeographic patterns among haplotypes of CR and alleles of S7 were analysed using the Median Joining Network method (Bandelt et al., 1999) implemented in Network (version 4.6.1.0; fluxus-engineering.com) that infers the most parsimonious branch connections between sampled haplotypes or alleles.
ARLEQUIN was also used to assess deviations from Hardy–Weinberg expectations using randomised distributions of FIS values with sequential Bonferroni correction (Rice, 1989), and to explore historical demography inferred by mismatch distributions. P-values were adjusted to avoid false positives using an optimised false discovery rate approach implemented in Q-value (Storey, 2002).
In order to assess the statistical power of our data sets to detect population genetic structure, a retrospective power analysis was performed using POWSIM 4.1 (Ryman and Palm, 2006). This program simulates a large number of populations that have been allowed to drift to user-defined levels of genetic divergence (FST). The program then samples these populations, and tests the null hypothesis of genetic homogeneity among populations using the χ2 approach and Fisher’s exact test. The percentage of significant outcomes (P<0.05 and P<0.01) from a large number of such samplings is interpreted as the power of the data to detect the defined level of genetic divergence. The level of genetic divergence is user defined by varying combinations of effective population size (Ne) and generations of drift (t). For CR, statistical power to detect different levels of FST by varying t with a fixed Ne was tested using 1000 dememorisations, 100 batches and 1000 interactions per batch. Analyses were performed to estimate the risk for false significance (type I error) and to identify the lowest level of genetic divergence that could be detected among our sampling sites with a power ⩾95% and ⩾99% using our actual study data.
Hierarchical analysis of molecular variance (Excoffier et al., 1992) was employed as a framework to test for alternative geographic groupings among the samples (specific designs are illustrated in the Results). In the case of the S7 intron, the analyses were also run in ARLEQUIN, after allowing the program to reconstruct the haplotypes present.
The software MicroChecker (Van Oosterhout et al., 2004) was used to check whether microsatellite allelic frequencies were likely to be affected by the presence of null alleles, and ARLEQUIN was employed to test for loci under selection, using the FST outlier approach, under the assumption of hierarchical population structure (Excoffier et al., 2009). Subsequently, expected and observed heterozygosity (He and Ho) and allelic richness, standardised on the smallest sample size (RA), were calculated using FSTAT 2.9.3 (Goudet, 1995), and Kruskal–Wallis nonparametric analysis of variance test was used to evaluate whether different populations had significantly different diversity levels. The FST genetic fixation (Weir and Cockerham, 1984) and Dest genetic differentiation (Jost, 2008) statistics were estimated with the diveRsity package 1.9.5 (Keenan et al., 2013). The variance of each statistic was assessed through the calculation of 10 000 pairwise bootstrapped 95% confidence limits using a bias corrected method that basically recentres the confidence interval (CI) around the initial parameter estimate. We employed both genetic estimators as they present advantages and drawbacks in quantifying population structure (for a discussion see Bird et al., 2001; Jost, 2008; Ryman and Leimar, 2009; Meirmans and Hedrick, 2010; Whitlock, 2011).
STRUCTURE 2.1 (Pritchard et al., 2000) was employed for the microsatellite data set to identify the most likely number and composition of population clusters in the data set irrespective of geographic location. An admixture model was used and 10 independent runs were performed for each K-value (1–10) using 500 000 iterations with a burn-in period of 100 000. Support for the optimal cluster structure was sought by examining both the averaged log-likelihood across runs for each K-value, and the relevant ΔK distribution according to Evanno et al. (2005).
Nonmetric multidimensional scaling (MDS) was inferred from pairwise FST and Dest matrices using the SMARCOF package 1.5-0 (De Leeuw and Mair, 2009) and MDS was employed to visually represent the genetic relationships among population samples, using microsatellite-, mtDNA- and S7-based matrices of differentiation. Correlation tests were used to assess the degrees of association between pairwise microsatellites and mtDNA using FST and Dest values. The ade4 R package 1.6-2 (Dray and Dufour, 2007) was used to perform correlation tests running comparisons between simulated (10 000 permutations) and observed data. BOTTLENECK 1.2 (Piry et al., 1999) was used to test for a recent expansion after a population reduction. The program tests for an excess of heterozygosity (He>Heq) based on the assumption that, following a bottleneck, the number of alleles in a population (from which the heterozygosity expected at equilibrium Heq is inferred) drops faster than classical Wright/Nei expected heterozygosity, He (Cornuet and Luikart, 1996). The program was run with 5000 iterations assuming a two-phase mutation model with a proportion of mutations that follow the stepwise mutation model set at 80%. In each population, the significance of He>Heq was assessed with a Wilcoxon sign-rank test.
We used approximate Bayesian computation (ABC) as implemented in the software DIYABC (Cornuet et al., 2008) to compare a more elaborate range of colonisation scenarios and identify the most likely historical reconstruction of the origin of D. vulgaris in the Azores, combining mtDNA CR and microsatellite data sets (see Results section for explanation of scenarios and relevant probabilistic support). The ‘reference table’ was built with 1 000 000 simulated data sets per scenario under three different simulations, the Beaumont, Cornuet–Miller and Guillemaud models, using a combination of summary statistics for the microsatellite data, following Stockwell et al. (2013), whereas for the mtDNA CR we used the following summary statistics: one-sample statistics for mean number of pairwise differences and variance of pairwise differences; two-sample statistics for number of segregating sites, mean of within-sample pairwise differences, mean of between-sample pairwise differences and FST between samples. In the Beaumont model, the summary statistics for the mtDNA CR were enriched taking into account Tajima’s D, number of haplotypes, number of segregating sites for one sample and two samples. For the microsatellites we used the default generalised stepwise mutation model with a mean mutation rate across loci set at 10−3–10−4, whereas for the mtDNA CR we implemented the Hasegawa–Kishino–Yano nucleotide substitution model with nonuniform evolutionary rates among sites (G=0.30 and I=1) and set a mean mutational rate at 4–12% per million years as a reliable estimate for sparid CR (Bargelloni et al., 2003). Population groupings were informed by prior analysis of population structure (see Results), and focussed specifically on the testing of Azorean colonisation. We used uniform priors for the three scenarios, and initially gave no constraints to effective population sizes (Ni) and coalescent events (ti) (see Supplementary Material online). Then we applied stricter ranges for both Ni and ti to verify robustness of estimates, Azores (AZ) N=1–500, Madeira+Portugal South+Cadiz (MAD+PTS+CAD) N=500–50 000, Portugal Central (PTC) N=500–50 000 and time of divergence for the Azorean sample (t1)=1–100 generations. Reliability of scenarios was visualised through principal component analysis, with summary statistics as variables, and posterior probabilities were compared by both logistic regression and direct estimates convergence using 1% of closest simulated data sets (details of additional comparative fits of principal component analysis plots can be found in the Supplementary Material online).
Results
Mitochondrial DNA control region
A 345-bp segment of the mtDNA control region was obtained from 227 individuals, yielding 116 haplotypes with 118 variable sites, 48 of which were parsimony informative. The percentage of private haplotypes (haplotypes only detected in a single location) was ca. 20% in the Azores sample, whereas in other sampling sites ranged between 50% (southern Portugal) and 78% (Cadiz and Mauritania). Overall haplotype diversity was high (h=0.983±0.004), whereas the corresponding nucleotide diversity was low (π=0.018±0.010). Haplotype diversity ranged from 0.688 to 1.000, whereas nucleotide diversity ranged from 0.012 to 0.017 (Table 1). Sequences from the Azores showed the lowest haplotypic diversity (0.668±0.035) and the second lowest nucleotide diversity (0.014±0.004). The 23 mtDNA CR sequences of D. vulgaris from the Azores contained only 5 haplotypes: the most common haplotypes (SH11, SH5 and SH14) were represented by 19 Azorean fish, 6 from Madeira, 1 from Cadiz, 3 from southern Portugal and 1 from the Balearics.
Estimates of α (type I) error calculated using power analyses indicated that the risk of false significance was below 5% (3.2% χ2) or just slightly above (5.7% Fisher’s exact test). When re-running the simulations using different values for drift in terms of generations, the power analyses indicated that the amount of genetic divergence detectable among our sampling sites with ⩾95% confidence (94.9% χ2, 96.8% Fisher’s exact test) was FST ⩾0.0129 (Ne=2500, t=65) and with ⩾99% confidence (98.9% χ2, 99.7% Fisher’s exact test) was FST ⩾0.0157 (Ne=2500, t=79). The overall FST value observed was 0.0524. Because of the high number of CR haplotypes, FST values were always smaller than Dest values (Figure 2 and Supplementary Table S1). When testing for pairwise comparisons involving the Azores, both measures of genetic differentiation were significant. For all other comparisons between sampling localities, the two indices agree only in Madeira vs Palermo, Canaries vs southern Portugal, Canaries vs Cadiz and Canaries vs Madeira. For the remaining comparisons, Dest values were significant and FST were not (Figure 2 and Supplementary Table S1).
Bar plots of population pairwise FST (in black) and Dest (in grey) for each of the marker type used in this study. ATL, Atlantic; AZO, Azores Is.; CAD, Cadiz; CAN, Canaries Is.; MA, Malta; MAD, Madeira Is.; MAU, Mauritania; PA, Palermo; PM, Palma de Mallorca (Balearic Is.); PTC, Portugal Centre (Sesimbra, Tejo and Sado estuary); PTS, Portugal South (Algarve, Arade and Lagos), TG, Torre Guaceto. *Statistical significance of differentiation was assessed through the calculation of 95% confidence limits out of 10 000 bootstrap replicates.
A series of hierarchical analyses of molecular variance were performed to identify the geographical groupings that best represented the spatial distribution of sequence diversity. The FSC/FCT ratio indicates the ratio between the level of variance within and between groups for each grouping level (Table 2). The grouping of localities with the lowest ratio was assumed to be the structured grouping that explained the greatest amount of genetic variation. The two-cluster option, in which only the Azores was separated from the other sampling locations, resulted in the largest between-group variance (FCT=0.107, P<0.001), with little differentiation among populations within the same geographical region (FSC=0.017, P<0.05). In the three-cluster option, in which the Mediterranean was separated, little improvement was observed: whereas no difference in the within-group variance component was found (FSC=0.015, P<0.05), the between-group variance was reduced by half (FCT=0.052, P<0.001). When Madeira was also separated from the rest of the Atlantic sites (four-cluster option), the FSC/FCT ratio dropped considerably mainly because of the negligible within-group variance (FSC=0.002, P=not significant) and no further reduction of the between-group structure (FCT=0.056, P<0.001). The mismatch analysis showed a unimodal distribution for all locations except the Azores (Supplementary Figure S1). The Tau (τ) values, which provide a rough estimate of when rapid changes in the populations have occurred, were similar in all instances (Supplementary Figure S1).
The haplotype network did not show any geographic pattern with regards to the Atlantic vs Mediterranean divide, or for any of the individual sampling sites (Figure 3). The most common haplotype found in the Azores was shared with Madeira, southern Portugal, Cadiz and the Mediterranean, and was included into a large reticulated clade. An independent lineage was found that included haplotypes from the Azores (one shared with Madeira and southern Portugal, and one unique) along with others from Portugal (centre and south), Canaries and the Mediterranean (Figure 3).
Haplotype relationships of D. vulgaris represented in a median joining network for mtDNA (CR) and nuclear DNA (S7). Haplotypes are represented by circles whose sizes are proportional to absolute frequencies in the total sample and the colours used represent the locations as indicated by the legend on the side.
S7 nuclear ribosomal DNA
The S7 nuclear region was represented by 127 unique alleles from a total of 274 sequences (138 individuals) and consisted of 271 bp, including 36 variable sites. Estimates of type I error calculated using power analyses indicated that the risk for false significance was below 5% (3.8% χ2, 4.6% Fisher’s exact test). When rerunning the simulations using different values for drift in terms of generations, the power analyses indicated that the amount of genetic divergence detectable among our sampling sites with ⩾95% confidence (94.0% χ2, 96.4% Fisher’s exact test) was FST ⩾0.0035 (Ne=10,000, t=70) and with⩾99% confidence (99.0% χ2, 99.4% Fisher’s exact test) was FST⩾0.0041 (Ne=10,000, t=82). The observed overall FST value was −0.0146.
FST pairwise values were generally smaller for S7 than for CR, and only four comparisons were significant (Torre Guaceto vs Madeira, Canaries, central and southern Portugal; Figure 2 and Supplementary Table S1). Dest, on the other hand, proved to be significant in all comparisons involving the Azores and in large part of the other comparisons (Figure 2 and Supplementary Table S1). The haplotype network did not reveal any geographical association among haplotypes and it appeared as a single large clade (Figure 3). Representatives from the Azores were widely spread and shared with all other localities (Figure 3).
Microsatellites
No null alleles or departures from neutrality were detected. Overall, private allele counts ranged between 0 (Torre Guaceto) and 26 (southern Portugal) (Table 1). In the Atlantic, the number of private alleles was smallest in the Azores, with similar low values also in central Portugal, Cadiz and Madeira (Table 1). Estimates of observed heterozygosity ranged from 0.784 in the Azores to 0.863 in Palermo, and none of the sampling sites were significantly more or less diverse from one another (Kruskal–Wallis test, P=0.792; Table 1). Similarly, allelic richness varied between 7.2 in Azores and 10.1 in Palermo and South Portugal and yet was not significantly different among locations (Kruskal–Wallis test, P=0.387). Tests for deviations from Hardy–Weinberg expectation were significant after Bonferroni correction only for Cadiz and Portugal Central. No significant signals of recent bottlenecks were detected, in particular in the focal Azorean population (one-tailed Wilcoxon sign-rank test for He excess, P=0.45). Estimates of type I error calculated using power analyses indicated that the risk of false significance was slightly above 5% (6.9% χ2, 7.1% Fisher’s exact test). When rerunning the simulations using different values for drift in terms of generations, the power analyses indicated that the amount of genetic divergence detectable among our sampling sites with ⩾95% confidence (96.1% χ2, 93.4% Fisher’s exact test) was FST ⩾0.0023 (Ne=10 000, t=47) and with ⩾99% confidence (98.8% χ2, 98.2% Fisher’s exact test) was FST ⩾0.0028 (Ne=10 000, t=57). The overall FST value across populations was however much larger: 0.0240.
The L(K) distribution obtained with STRUCTURE showed the largest likelihoods for K-values between 1 and 4 (Supplementary Figure S2A) and the highest ΔK value is for K=2 (Supplementary Figure S2B). The compositional bar plot for K=2 provided a hint for the Azores divergence, but for K=3–4 the pattern was more evident (Supplementary Figure S3). All pairwise FST and Dest comparisons involving Azores returned the highest values when compared with all other groups, whereas no significance was detected by both indices for intra-Mediterranean pairwise comparisons (Figures 2 and 4a and Supplementary Table S1).
Combined marker analyses
MDS plots based on pairwise FST matrices from microsatellites and mtDNA markers returned a strong spatial pattern compared with S7 (Figures 4a–f). On the other hand, Dest-based MDS plots displayed a geographical pattern only with microsatellite data (Figure 4b). The finer resolution provided by microsatellite markers highlighted the Atlantic–Mediterranean spatial divide and the arrangement displayed in the Dest plot clustered locations into two groups accordingly to their oceanographic basin (Figure 4b). Contrasting patterns were shown by the MDS plots based on CR data, using both measures of differentiation (Figures 4c and d). The plot based on pairwise FST values resembled the pattern seen for the microsatellites but with a greater distance for the Azores and less discrimination among all Atlantic-Mediterranean locations (Figure 4c). On the contrary, the MDS plot computed from the Dest matrix did not show any indication of explicit spatial clustering, with the Azores positioned in proximity of the Balearics, then Cadiz, Madeira and, further distant, southern Portugal (Figure 4d). There was a pronounced correlation observed between the FST values of microsatellite and CR (r=0.851; P=0.034), but no correlation was observed when comparing the Dest values (r=0.166; P=0.204) for the same two markers (Figure 5). No correlation was detected in matrix comparisons between microsatellites and S7 (FST: r=0.009, P=0.354; Dest: r=0.243, P=0.132) and CR against S7 (FST: r=0.166, P=0.160; Dest: r=0.052, P=0.369).
Multidimensional scaling plot based on the matrix of FST pairwise comparisons from microsatellites (a and b), mtDNA CR (c and d) and S7 (e and f) data sets, respectively. PTC, Portugal Centre (Sesimbra, Tejo and Sado estuary); PTS, Portugal South (Algarve, Arade and Lagos). Dark grey dot refers to Atlantic and light grey triangles refer to Mediterranean samples.
Microsatellite against mtDNA CR for the FST and Dest matrices using all sampling localities. A significant correlation using all data is reported only for the FST matrices (r=0.851; P=0.034), whereas it is not significant when comparing the Dest matrices (r=0.166; P=0.204). When data are treated separately as ‘only Azores comparisons’ (dark grey dot, upper trendline) and ‘excluding Azores comparisons’ (light grey triangles, lower trendline), the pairwise comparisons within each one of these two ‘clouds’ also show lack of correlation.
The three most realistic ABC scenarios consisted of comparing the Azores with two other potential source populations that comprised Madeira+Portugal and South+Cadiz, on one hand, and Portugal Centre on the other (Figure 6a). The best supported scenario consisted of an initial split between Madeira+Portugal South+Cadiz and Portugal Centre, followed by dispersal and colonisation of the Azores from Madeira+Portugal South+Cadiz (Figure 6b and Supplementary Figure S4). The summary statistics for this scenario were in the range of the simulated values with the exception of the Cornuet–Miller model, in which the Garza Williamson’s M observed values for the Madeira+Portugal South+Cadiz sample fell in the 0.1% distribution tail. The simulations using the Beaumont, Cornuet–Miller and Guillemaud models provided similar estimates of long-term effective population sizes (Ne) and times of divergence (Table 3). For the three most realistic scenarios, the prior intervals of N=1–500 for Azores and t1=1–100 allowed for an optimised fit of the posterior distributions of the observed data (Figure 6). For the Azores, the Ne median value varied from 283 to 312 and for Madeira+Portugal South+Cadiz values ranged between 36 700 and 39 600. The median value of the posterior distribution for times of coalescence between these two populations varied between 41.2 (95% CI: 5.5–83.6) and 52.4 (95% CI: 6.32–89.0) generations (Figure 6b and Table 3) equivalent to roughly 80–150 years, assuming generation times of 2–3 years (Hadj Taieb et al., 2013).
(a) The three most realistic ABC scenarios comparing the Azorean sample (AZ) with two other potential source populations. (b, left) Reliability of all scenarios under the three models (I=Cornuet–Miller; II=Beaumont; III=Guillemaud) visualised through posterior probabilities as the relative proportions (direct estimates) and logistic regressions (red, green and blue represent the parameters associated to the scenarios 1, 2 and 3, respectively). (b, right) Principal component analysis (PCA) showing the good fit of posterior distributions for scenario 1 under the three models (the observed data—large yellow spots—fall in the clouds of the dots representing the posterior (larger red dots) and the prior (smaller red dots) distributions). CAD, Cadiz; MAD, Madeira Is.; PTC, Portugal Centre (Sesimbra, Tejo and Sado estuary); PTS, Portugal South (Algarve, Arade and Lagos).
Discussion
This phylogeographic study revealed that the recent appearance of D. vulgaris in the Azores is unlikely to have been derived from an ancient population, as, despite evidence for strong differentiation, there is no indication of lineage divergence or a conspicuous presence of private alleles. We propose that the origin of the species in the Azores is compatible with the occurrence of rare dispersal events that led to a recent successful establishment of the fish around these oceanic islands. Before discussing these findings in detail, we address two possible caveats: the small sample size for some locations and the short fragment length of mtDNA CR and nuclear S7 markers, 345 and 271 bp long. Although the number of specimens collected for most of the sites was <50, they provided a sufficient level of diversity to accurately estimate haplotype frequencies (Hale et al., 2012). POWSIM indicated that a type II error because of low power was unlikely (probability >0.95) (CR: FST=0.0129–0.0157, S7: FST=0.0035–0.0041 and microsatellites: FST=0.0023–0.0028). These values are far lower than the FST values empirically detected between the Azores and any other sampling sites (CR: FST=0.1410–0.2370, S7: FST=0.0069–0.0583 and microsatellites: FST=0.0477–0.0687). In terms of sequence length, besides the POWSIM indications, it is noteworthy that the mtDNA CR and nuclear S7 have displayed adequate informative variation to tackle phylogeographic problems and those exact fragments have been successfully used in other comparable studies (see, for example, Bargelloni et al., 2005; Domingues et al., 2007a, b). We therefore conclude that the molecular toolkit employed here is fit to address the focal questions.
Population structure: Azores vs other locations
Although evidence provided by the three markers is not always congruent, there is nonetheless support for the genetic distinctiveness of the Azores population: (1) analysis of molecular variance on mtDNA CR indicates a four-cluster structure ([AZ] [MAD] [Atlantic] [Mediterranean]) as the grouping that explained the greatest amount of genetic variation (Table 2); (2) mtDNA, S7 and microsatellite FST and Dest values are significant in all pairwise comparisons involving the Azores (Figure 2 and Supplementary Table S1); and (3) microsatellite FST and Dest and mtDNA CR FST MDS plots return a consistent pattern of Azores separation (Figures 2 and 4). Similarly, this spatial arrangement is supported by the correlation between CR and microsatellite FST matrices (Figure 5). Only the mtDNA CR Dest matrix and the S7 marker fail to differentiate the Azorean fish from the others (Supplementary Table S1 and Figures 4d–f). This can possibly be due to the presence of several shared haplotypes between the Azores and the other sampling sites for the mtDNA CR (Figures 1 and 3) and the typically slow-evolving nature of the S7 nuclear region (Lessios, 2008).
The population structure for D. vulgaris might be explained by the mechanism that has led this species to reach the Azores. Pioneer expansion, as described in Horne (2014), can have a substantial role in marine connectivity. This type of expansion occurs primarily with rare, long-distance dispersal events (that is, small contingents of colonisers settled in the Azores), and populations diverge through a ‘reshuffling effect’ where available polymorphisms may be stochastically sorted in the new habitat through coloniser admixture (see Horne, 2014 and references therein), and not only through genetic drift.
Recent colonisation or demographic expansion of an old population?
The ABC results point to a contemporary (80–150 years ago) divergence between the Azores and the most likely populations of origin. The lack of long-term signature of independent lineages at the most evolutionarily conservative markers constitutes further support of a recent origin of the Azorean population. Moreover, the trend for lower diversity in the Azores provides some indications of reduced effective size in this population (confirmed by the estimates obtained through ABC; the number of microsatellite private alleles is 4 and private mtDNA CR haplotypes is only 1). On the other hand, microsatellites indicate no significant signals of recent bottlenecks in the Azorean population, although the comparatively low number of both private haplotypes and private alleles in that population further points to a small ‘reshuffled’ pioneer unit (sensu, Horne, 2014) that has diverged from continental source populations, in isolation for a relatively short time.
Simulations using ABC provide estimates that are consistent with the hypothesis that the Azorean D. vulgaris reached the archipelago as a result of rare dispersal events from the neighbouring Atlantic islands and continental localities over the past century (Figure 6b). The assumption that the other oceanic island of Madeira might have acted as a stepping-stone for most of the warm water fish fauna of the Azores (Santos et al., 1995) is a plausible framework to interpret the demographic dynamic of D. vulgaris, and the ABC approach offers support to this hypothesis. The broad confidence intervals (95% CI: 11–267 years ago) around the ABC estimates (80–150 years ago) do not exclude the possibility of an even more recent colonisation event that appears to be supported by the lack of visual/catch records of this species. On the other hand, we cannot discount the possibility that D. vulgaris sightings may have been favoured by the recent boom in scuba-diving tourism in the Azores and the intensive visual census monitoring programs supported by the Department of Oceanography and Fisheries of the University of the Azores since the 1990s that has increased the focus on coastal species compared with a traditional emphasis on the deeper water species targeted by commercial fisheries and scientific surveys.
Scenario reconstruction
The exhaustive probabilistic approach offered by ABC supports the hypothesis of rare dispersal events that led to the establishment of the Azorean population, providing estimates of Ne and times of divergence that are similar in the three models (Figure 6b and Table 3). The time elapsed between initial colonisation and the onset of rapid population growth is a process that involves ecological and evolutionary adaptations, and thus the time required to overcome these constrains varies among species (Gaither et al., 2012). Prolonged time lags might occur during any phase of the invasion process, subsequently affecting their range of expansion (Sakai et al., 2001; Crooks, 2005). It seems therefore possible that D. vulgaris reached the Azores in low numbers perhaps as early as in the nineteenth century. Populations may have been small and/or ephemeral and possibly the environmental conditions were not favourable to the expansion of larger demographic units. Nevertheless, an even more recent colonisation of D. vulgaris within the past two decades (as faunal records suggest; Afonso et al., 2013), or a sudden population expansion following an earlier dispersal events, could be linked to a recent rising of the sea surface temperature (SST). This species is less adapted to cool waters than some of its congenerics, for example, D. sargus, that is reported to extend its distribution to higher latitudes (for a review see Patarnello et al., 2007). The increased SST may have created more suitable habitat conditions for this species in the Azores and favoured its establishment, as temperature-driven distributional shifts in marine organisms have not been uncommon occurrences in the past two decades (Attrill and Power, 2002; Perry et al., 2005; Belanger et al., 2012). The global mean SST values for 1980–1994 and 1995–2005 were 11.1±0.1 °C and 11.7±0.1 °C, respectively (Rayner et al., 2006). The SST over the latter period averaged ∼0.6 °C warmer than the preceding 15 years (consistent with Figure 14d in Rayner et al., 2006).
The colonisation of an oceanic archipelago by a littoral species in historical times represents a notable example of the effectiveness of sporadic larval dispersal events in suitable climatic conditions (Lessios and Robertson, 2006). The temperature rise that affected the North-East Atlantic sea surface waters caused an impact on the circulation patterns around the Azores. In this stretch of ocean, currents are predominantly south-eastern, therefore heading in opposite directions to favour any passive dispersal of larvae from the neighbouring Madeira toward the Azores. However, historical data series indicate episodic anomalies of the SST (mainly in autumn and winter) during which surface currents moved in the opposite direction, and could have enhanced the dispersals of this species to the Azores (Santos et al., 1995). Episodic anomalies are likely to determine temporal ‘pulses’ of drops and surges of species diversities with different adaptations to temperature (see, for example, Stefanni et al., 2006). Moreover, the reproductive period for D. vulgaris is between November and March with a pelagic larval duration of 29–58 days (Galarza et al., 2009), endowing this species with at least the potential for ‘oceanic leaps’ if conditions are suitable.
Implications for fundamental and applied tasks
Collective evidence indicates that the Azorean population of D. vulgaris may have originated from waves of colonisers from neighbouring Atlantic localities within the past centuries, and demographically expanded more recently. What is unclear is the number of generations incurred between the initial period of colonisation to the time at which the presence of this species reached a substantial number of individuals to become conspicuous and therefore detectable by local fishermen and divers. Ecological, historical and environmental data support the view that stochastic events, coupled with favourable climatic conditions, may lead to the establishment of new founding populations at the edge of the distribution range. However, the discrepancy between the centuries vs decadal time frames suggested by molecular data and observational records respectively indicate that there may be a time lag between founding at the range edge and a successful population establishment (see, for example, Crooks, 2005; Gaither et al., 2012). This will likely depend on the interplay between the life history traits of the coloniser and the ecosystem structure of the colonised habitat (Sakai et al., 2001). Although D. vulgaris is not considered a valuable fishery resource, the same dynamics that led to its colonisation (over centuries) and increase (over decades) may well apply to other species with similar life histories, but greater attractiveness for exploitation, such as the case of recently expanding populations of gilt-head seabream (Sparus aurata) in northern Europe (Coscia et al., 2012). Such demographic processes should be taken into consideration in models that aim at improving both exploitation management and designing protected areas.
Data archiving
Sequence data have been submitted to GenBank: accession numbers HQ997776–HQ997893, JQ655470–JQ655598 and JQ624680–JQ624764.
Genotype data have been submitted to Dryad: 10.5061/dryad.bd6h3.
Data available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.bd6h3.
References
Afonso P, Porteiro FM, Fontes J, Tempera F, Morato T, Cardigos F et al. (2013). New and rare coastal fishes in the Azores islands: occasional events or tropicalization process? J Fish Biol 83: 272–294.
Attrill MJ, Power M . (2002). Climatic influence on a marine fish assemblage. Nature 417: 275–278.
Bandelt H-J, Forster P, Röhl A . (1999). Median-joining networks for inferring intraspecific phylogenies. Mol Biol Evol 16: 37–48.
Bargelloni L, Alarcon JA, Alvarez MC, Penzo E, Magoulas A, Palma J et al. (2005). The Atlantic-Mediterranean transition: discordant genetic patterns in two seabream species, Diplodus puntazzo (Cetti) and Diplodus sargus (L.). Mol Phylogenet Evol 36: 523–535.
Bargelloni L, Alarcon JA, Alvarez MC, Penzo E, Magoulas A, Reis C et al. (2003). Discord in the family Sparidae (Teleostei): divergent phylogeographical patterns across the Atlantic-Mediterranean divide. J Evol Biol 16: 1149–1158.
Belanger CL, Jablonski D, Roy K, Berke SK, Krug AZ, Valentine JW . (2012). Global environmental predictors of benthic marine biogeographic structure. Proc Natl Acad Sci USA 109: 14046–14051.
Bird CE, Smouse PE, Karl SA, Toonen RJ . (2001) Detecting and measuring genetic differentiation. In: Koenemann S, Held C, Schubart C (eds). Crustacean Issues: Phylogeography and Population Genetics in Crustacea. CRC: Boca Raton: Florida pp 31–55.
Chopelet J, Waples R, Mariani S . (2009). Sex change and the genetic structure of marine fish populations. Fish Fish 10: 329–343.
Chow S, Hazama K . (1998). Universal PCR primers for S7 ribosomal protein gene introns in fish. Mol Ecol 7: 1255–1256.
Cornuet JM, Luikart G . (1996). Description and power analysis of two tests for detecting recent population bottlenecks from allele frequency data. Genetics 144: 2001–2014.
Cornuet JM, Santos F, Beaumont MA, Robert CP, Marin JM, Balding DJ et al. (2008). Inferring population history with DIY ABC: a user-friendly approach to approximate Bayesian computation. Bioinformatics 24: 2713–2719.
Coscia I, Vogiatzi E, Kotoulas G, Tsigenopouls CS, Mariani S . (2012). Exploring neutral and adaptive processes in expanding populations of gilthead sea bream, Sparus aurata L., in the North-East Atlantic. Heredity 108: 537–546.
Costagliola D, Robertson DR, Guidetti P, Stefanni S, Wirtz P, Heiser JB et al. (2004). Evolution of coral reef fish Thalassoma spp. (Labridae). 2. Evolution of the eastern Atlantic species. Marine Biol 144: 377–383.
Crooks JA . (2005). Lag times and exotic species: the ecology and management of biological invasions in slow-motion. Ecoscience 12: 316–329.
De Leeuw J, Mair P . (2009). Multidimensional scaling using majorization: SMACOF in R. J Stat Softw 31: 1–30.
Domingues VS, Faria C, Stefanni S, Santos R, Brito A, Almada VC . (2007a). Genetic divergence in the Atlantic-Mediterranean Montagu's blenny, Coryphoblennius galerita (Linnaeus 1758) revealed by molecular and morphological characters. Mol Ecol 16: 3592–3605.
Domingues VS, Santos RS, Brito A, Alexandrou M, Almada VC . (2007b). Mitochondrial and nuclear markers reveal isolation by distance and effects of Pleistocene glaciations in the northeastern Atlantic and Mediterranean populations of the white seabream (Diplodus sargus, L.). J Exp Marine Biol Ecol 346: 102–113.
Dray S, Dufour AB . (2007). The ade4 package: implementing the duality diagram for ecologists. J Stat Softw 22: 1–20.
Evanno G, Regnaut S, Goudet J . (2005). Detecting the number of clusters of individuals using the software STRUCTURE: a simulation study. Mol Ecol 14: 2611–2620.
Excoffier L, Foll M, Petit RJ . (2009). Genetic consequences of range expansions. Annu Rev Ecol Evol Syst 40: 481–501.
Excoffier L, Laval G, Balding D . (2003). Gametic phase estimation over large genomic regions using an adaptive window approach. Hum Genomics 1: 7–19.
Excoffier L, Lischer HEL . (2010). Arlequin suite ver 3.5: a new series of programs to perform population genetics analyses under Linux and Windows. Mol Ecol Resour 10: 564–567.
Excoffier L, Smouse PE, Quattro JM . (1992). Analysis of molecular variance inferred from metric distances among DNA haplotypes - application to human mitochondrial-DNA restriction data. Genetics 131: 479–491.
Francisco SM, Almada VC, Faria C, Velasco EM, Robalo JI . (2014). Phylogeographic pattern and glacial refugia of a rocky shore species with limited dispersal capability: the case of Montagu’s blenny (Coryphoblennius galerita, Blenniidae). Marine Biol 161: 2509–2520.
Gaither MR, Toonen RJ, Bowen BW . (2012). Coming out of the starting blocks: extended lag time rearranges genetic diversity in introduced marine fishes of Hawaii. Proc R Soc B Biol Sci 279: 3948–3957.
Galarza JA, Carreras-Carbonell J, Macpherson E, Pascual M, Roques S, Turner GF et al. (2009). The influence of oceanographic fronts and early-life-history traits on connectivity among littoral fish species. Proc Natl Acad Sci USA 106: 1473–1478.
Goudet J . (1995). FSTAT V1.2. A computer program to calculate F-statistics. J Hered 86: 485–486.
Hadj Taieb A, Ghorbel M, Ben Hadj Hamida N, Jarboui O . (2013). Reproductive biology, age and growth of the two banded seabream Diplodus vulgaris (Pisces: Sparidae) in the Gulf of Gabes, Tunisia. J Mar Biol Ass UK 93: 1415–1421.
Hale ML, Burg TM, Steeves TE . (2012). Sampling for microsatellite-based population genetic studies: 25 to 30 individuals per population is enough to accurately estimate allele frequencies. PLoS One 7: e45170.
Hilgendorf F . (1888). Die Fische der Azoren. Arch Naturgesch 54: 205–213.
Horne JB . (2014). Thinking outside the barrier: neutral and adaptive divergence in Indo-Pacific coral reef faunas. Evol Ecol 28: 991–1002.
Jost L . (2008). G' ST and its relatives do not measure differentiation. Mol Ecol 17: 4015–4026.
Keenan K, McGinnity P, Cross TF, Crozier WW, Prodöhl PA . (2013). DiveRsity: an R package for the estimation and exploration of population genetics parameters and their associated errors. Methods Ecol Evol 4: 782–788.
Lessios HA . (2008). The great American schism: divergence of marine organisms after the rise of the Central American isthmus. Annu Rev Ecol Evol Syst 39: 63–91.
Lessios HA, Robertson DR . (2006). Crossing the impassable: genetic connections in 20 reef fishes across the eastern Pacific barrier. Proc R Soc B Biol Sci 273: 2201–2208.
Mariani S, Maccaroni A, Massa F, Rampacci M, Tancioni L . (2002). Lack of consistency between the trophic interrelationships of five sparid species in two adjacent central Mediterranean coastal lagoons. J Fish Biol 61: 138–147.
Meirmans PG, Hedrick PW . (2010). Assessing population structure: FST and related measures. Mol Ecol Resour 11: 5–18.
Ostellari L, Bargelloni L, Penzo E, Patarnello P, Patarnello T . (1996). Optimization of single-strand conformation polymorphism and sequence analysis of the mitochondrial control region in Pagellus bogaraveo (Sparidae, Teleostei): rationalized tools in fish population biology. Anim Genet 27: 423–427.
Patarnello T, FAMJ Volckaert, Castilho R . (2007). Pillars of Hercules: is the Atlantic-Mediterranean transition a phylogeographical break? Mol Ecol 16: 4426–4444.
Perry AL, Low PJ, Ellis JR, Reynolds JD . (2005). Climate change and distribution shifts in marine fishes. Science 308: 1912–1915.
Piry S, Luikart G, Cornuet JM . (1999). BOTTLENECK: a computer program for detecting recent reductions in the effective population size using allele frequency data. J Hered 90: 502–503.
Pritchard JK, Stephens M, Donnelly P . (2000). Inference of population structure using multilocus genotype data. Genetics 155: 945–959.
Rayner NA, Brohan P, Parker DE, Folland CK, Kennedy JJ, Vanicek M et al. (2006). Improved analyses of changes and uncertainties in sea surface temperature measured in situ since the mid-nineteenth century: the HadSST2 dataset. J of Climate 19: 446–469.
Ryman N, Leimar O . (2009). GST is still a useful measure of genetic differentiation - a comment on Jost's D. Mol Ecol 18: 2084–2087.
Ryman N, Palm S . (2006). POWSIM: a computer program for assessing statistical power when testing for genetic differentiation. Mol Ecol Resour 6: 600–602.
Rice WR . (1989). Analyzing tables of statistical tests. Evolution 43: 223–225.
Roques S, Galarza A, Macpherson E, Turner GF, Carreras-Carbonell J, Rico C . (2007a). Isolation of eight microsatellites loci from the saddled bream, Oblada melanura and cross-species amplification in two sea bream species of the genus Diplodus. Conserv Genet 8: 1255–1257.
Roques S, Galarza A, Macpherson E, Turner GF, Rico C . (2007b). Isolation and characterization of nine polymorphic microsatellite markers in the two-banded sea bream (Diplodus vulgaris) and cross-species amplification in the white sea bream (Diplodus sargus) and the saddled bream (Oblada melanura). Mol Ecol Notes 7: 661–663.
Sakai AK, Allendorf FW, Holt JS, Lodge DM, Molofsky J, With KA et al. (2001). The population biology of invasive species. Annu Rev Ecol Syst 32: 305–332.
Santos RS, Hawkins S, Monteiro LR, Alves M, Isidro EJ . (1995). Marine research, resources and conservation in the Azores. Aquat Conserv Mar Freshwat Ecos 5: 311–354.
Santos RS, Porteiro F, Barreiros J . (1997). Marine fishes of the Azores: annotated check-list and bibliography. Arquipélago Life Mar Sci (Suppl 1): 1–231.
Santos RS, Nash RDM . (1995). Seasonal-changes in a sandy beach fish assemblage at Porto-Pim, Faial, Azores. Estuar Coast Shelf Sci 41: 579–591.
Stefanni S, Domingues V, Bouton N, Santos R, Almada F, Almada VC . (2006). Phylogeny of the shanny, Lipophrys pholis, from the NE Atlantic using mitochondrial DNA markers. Mol Phylogenet Evol 39: 282–287.
Stockwell CA, Heilveil JS, Purcell K . (2013). Estimating divergence time for two evolutionarily significant units of a protected fish species. Conserv Genet 14: 215–222.
Storey JD . (2002). A direct approach to false discovery rates. J R Stat Soc B Stat Method 64: 479–498.
Thompson JD, Gibson TJ, Plewniak F, Jeanmougin F, Higgins DG . (1997). The CLUSTAL_X windows interface: flexible strategies for multiple sequence alignment aided by quality analysis tools. Nucleic Acids Res 25: 4876–4882.
Van Oosterhout C, Hutchinson WF, Wills DPM, Shipley P . (2004). MICRO-CHECKER: software for identifying and correcting genotyping errors in microsatellite data. Mol Ecol Notes 4: 535–538.
Whitehead PJP, Bauchot ML, Hureau JC, Nielsen J, Tortonese E . (1986) Fishes of the North-Eastern Atlantic and the Mediterranean. Unesco: Paris. Volume I–III: 1–1473.
Whitlock MC . (2011). G' ST and D do not replace F ST . Mol Ecol 20: 1083–1091.
Wier BS, Cockerham CC . (1984). Estimating F-Statistics for the analysis of population structure. Evolution 38: 1358–1370.
Acknowledgements
We appreciate the skilful technical assistance provided by S Chenu, A Pereira and Carlotta Sacchi. This work was supported by the MarinERA project ‘Marine phylogeographic structuring during climate change: the signature of leading and rear edge of range shifting populations’ and by the Eco-Ethology Research Unit (PEst-OE/MAR/UI0331/2011, Fundação para a Ciência e Tecnologia, partially FEDER funded). The collection of fish and the monitoring census benefit from work done through the past projects: CLIPE, MAREFISH, MARÉ, MAROV, OGAMP, MARMAC, MARMAC II. SS is a research fellow supported by the Marie Curie Grant co-funded by the EU under the FP7-People-2012-COFUND; Co-funding of Regional, National and International Programmes, GA no. 600407 and the Bandiera Project RITMARE. SMF was supported by an FCT Grant (SFRH/BPD/84923/2012). IMAR-Univ Azores was funded through the pluriannual and programmatic funding scheme as research unit 531 and associate laboratory LARSyS 9, with financial support from OE and COMPETE, through FCT and DRCTC/GovAzores. We are also extremely grateful to Norberto Serpa, Azores, Marta Linde, Balearic Islands, Molly Buchholz-Sørensen, Malta, Paolo Guidetti and Marco Arculeo, Italy, for collecting samples. This work has benefited greatly from the comments of Per Erik Jorde from the University of Oslo and three anonymous reviewers.
We dedicate this paper to the memory of our dear professor, colleague and friend Vítor Almada who prematurely died during the course of this work.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Supplementary Information accompanies this paper on Heredity website
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/
About this article
Cite this article
Stefanni, S., Castilho, R., Sala-Bozano, M. et al. Establishment of a coastal fish in the Azores: recent colonisation or sudden expansion of an ancient relict population?. Heredity 115, 527–537 (2015). https://doi.org/10.1038/hdy.2015.55
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/hdy.2015.55
This article is cited by
-
Against all odds: a tale of marine range expansion with maintenance of extremely high genetic diversity
Scientific Reports (2020)
-
Unravelling population genetic structure with mitochondrial DNA in a notional panmictic coastal crab species: sample size makes the difference
BMC Evolutionary Biology (2016)