Comparing G: multivariate analysis of genetic variation in multiple populations

Aguirre, J D; Hine, E; McGuigan, K; Blows, M W

doi:10.1038/hdy.2013.12

Download PDF

Original Article
Published: 13 March 2013

Comparing G: multivariate analysis of genetic variation in multiple populations

J D Aguirre¹,
E Hine¹,
K McGuigan¹ &
…
M W Blows¹

Heredity volume 112, pages 21–29 (2014)Cite this article

8293 Accesses
79 Citations
1 Altmetric
Metrics details

Subjects

Abstract

The additive genetic variance–covariance matrix (G) summarizes the multivariate genetic relationships among a set of traits. The geometry of G describes the distribution of multivariate genetic variance, and generates genetic constraints that bias the direction of evolution. Determining if and how the multivariate genetic variance evolves has been limited by a number of analytical challenges in comparing G-matrices. Current methods for the comparison of G typically share several drawbacks: metrics that lack a direct relationship to evolutionary theory, the inability to be applied in conjunction with complex experimental designs, difficulties with determining statistical confidence in inferred differences and an inherently pair-wise focus. Here, we present a cohesive and general analytical framework for the comparative analysis of G that addresses these issues, and that incorporates and extends current methods with a strong geometrical basis. We describe the application of random skewers, common subspace analysis, the 4th-order genetic covariance tensor and the decomposition of the multivariate breeders equation, all within a Bayesian framework. We illustrate these methods using data from an artificial selection experiment on eight traits in Drosophila serrata, where a multi-generational pedigree was available to estimate G in each of six populations. One method, the tensor, elegantly captures all of the variation in genetic variance among populations, and allows the identification of the trait combinations that differ most in genetic variance. The tensor approach is likely to be the most generally applicable method to the comparison of G-matrices from any sampling or experimental design.

Correlational selection in the age of genomics

Article 15 April 2021

Principal Component Analyses (PCA)-based findings in population genetic studies are highly biased and must be reevaluated

Article Open access 29 August 2022

Polygenic adaptation: a unifying framework to understand positive selection

Article 29 June 2020

Introduction

The distribution of genetic variation among multiple traits is a key determinant of how a population will respond to selection (Lande, 1979; Schluter, 1996; Arnold et al., 2001). For the prediction of evolutionary responses, the genetic variation in multiple traits is described by the symmetrical genetic variance–covariance matrix, G (Lande, 1980; Phillips and McGuigan, 2006). Genetic variances, and particularly covariances, depend on underlying genetic details such as the frequencies of alleles and the distribution of their effect sizes (Barton and Turelli, 1987; Turelli, 1988; Turelli and Barton, 1990), and hence are subject to change under both drift and selection. It is therefore reasonable to expect that the genetic variance in multiple traits might differ among populations, and consequently that the responses of these populations to the same selective force might also differ.

Although determination of the genetic details underpinning G is an active research area (Kelly, 2009), the general lack of information on the distribution of allelic effects and frequencies currently makes it impossible for theoretical quantitative genetic models to clearly predict the evolutionary dynamics of G. Several studies have circumvented this problem through simulation-based approaches, exploring the impact of variation in parameters describing evolutionary processes (selection, mutation and migration) on the evolution of G (Jones et al., 2003, 2004; Guillaume and Whitlock, 2007; Jones et al., 2007; Revell, 2007). These studies have demonstrated that G will evolve to the greatest extent in small populations, under weak correlational selection on traits, through directional selection against major axes of G, and when mutational correlation among traits is low. Simulated parameter ranges are based on information from nature (see Arnold et al. (2008)), but nonetheless, we typically lack information on multivariate mutation and selection, and on migration in specific natural populations and for multivariate trait sets of interest. It remains an empirical question whether G typically varies among populations in ways that will impact on their future responses to selection.

Numerous empirical studies have taken a comparative approach to determine evolutionary rates, and the processes affecting G (Steppan et al., 2002; Arnold et al., 2008). Although G-matrices are highly conserved among some populations (see Arnold et al. (2008)), they have also been demonstrated to rapidly diverge among both natural populations and experimental treatments (Cano et al., 2004; Doroszuk et al., 2008; Hine et al., 2009; Johansson et al., 2012). Laboratory manipulations have demonstrated that G can evolve rapidly in response to drift (Phillips et al., 2001), and that selection can drive rapid and repeatable evolution of G (Blows and Higgie, 2003; Hine et al., 2011). Further, the reproduction by experimental evolution of patterns observed in G among natural populations (Blows and Higgie, 2003), and the observations that the strength (Hunt et al., 2007) and pattern (Roff and Fairbairn, 2012) of selection are associated with levels of genetic variation in populations suggest selection might have a discernible effect on G.

Logistical limitations on estimating quantitative genetic parameters, particularly the need for relatively large samples, have restricted the utility of comparative quantitative genetics. However, more generally, the identification and interpretation of the variation among G-matrices has been limited by the lack of an appropriate statistical framework, a long-standing and ongoing analytical challenge (Turelli, 1988; Steppan et al., 2002; Hansen and Houle, 2008; Marroig et al., 2011; Roff et al., 2012). Various properties of symmetrical matrices can be described by summary parameters such as their size (the trace), measures of their ill-conditioned nature or eccentricity (Jones et al., 2003; Kirkpatrick, 2009), and the correlation among matrix elements (Roff et al., 2012). More complex hypotheses concerning proportionality, and a series of partial trait combination (principal component) comparisons using a hierarchy of similarity can also be tested (Flury, 1988; Phillips and Arnold, 1999).

There are a number of drawbacks that are shared by many of these current approaches. First, the majority of methods use metrics that do not clearly relate to evolutionary theory (Hansen and Houle, 2008), making it difficult to connect divergence in G to simple changes in genetic variance and the response to selection. Second, comparisons are typically made in the absence of any specific information on the direction of selection, and information on selection cannot be readily incorporated into some metrics. Third, many approaches can be applied only to data derived from simple experimental designs and are not well suited for applications involving the more complex experimental designs typically employed in experimental evolution studies or replicated sampling from different environments in the field. Finally, approaches for comparing G are typically focused on differences between pairs of populations, with no simple generalisation to multi-population studies. We are therefore lacking an analytical approach that is generally applicable across the data structures typical of studies in experimental and natural populations, which can be used to provide statistical confidence in inferred differences, and which can be used to predict differences between populations in their ongoing evolution. Our aim in this paper is to provide a cohesive and general analytical framework for comparative quantitative genetics that incorporates and extends existing geometric approaches, as it is the geometry of G that generates evolutionary constraints and determines the extent to which particular traits will respond to a given episode of selection (Walsh and Blows, 2009).

The response of a population to a particular vector of selection gradients (β) for a set of n traits is given by (Lande, 1979):

where G rotates (and scales) the response away from the direction of β, resulting in some level of genetic constraint (Walsh and Blows, 2009); the geometry of G determines the bias in the response to selection. Although individual traits feature as the rows and columns of G, it is important to realise that these individual measured traits do not necessarily have a greater role in the response to selection than any combination of the traits. Recognising G as simply characterising the level of genetic variance in all possible trait combinations (Blows and Hoffmann, 2005) provides a point of departure for the framework we outline in this paper for establishing how G differs among populations, and the evolutionary consequences of those differences.

To begin, consider how the genetic variance in any trait combination can be found using the projection (Lin and Allaire, 1977):

where b is scaled to unit length. It is the relative orientation of the direction of b to the distribution of genetic variance in G that determines how biased the response will be away from b when selection is applied in this direction. The distribution of genetic variances in G can be represented by the eigenvalues (λ) of G, that is, by the genetic variances of the orthogonal trait combinations described by the eigenvectors. Most estimated G tend to be ill-conditioned, displaying an exponential-like decay in λ (Kirkpatrick, 2009). The influence of the λ_i and its corresponding eigenvectors (g_i) on the response to selection can be shown using a spectral decomposition of the multivariate breeders’ equation (Walsh and Blows, 2009):

When genetic variation is much larger in some trait combinations than others (for example, the λ decay exponentially), there are two possible consequences for the response to selection that are not apparent from the consideration of single trait heritabilities and selection gradients. First, individual traits might respond to selection in the direction opposite to their selection gradient. Second, the set of correlated traits might respond overall in a direction that is substantially different from the direction of selection applied (that is, β). Both these possible outcomes become more likely as the magnitude of genetic variation becomes smaller in the direction of selection relative to other trait combinations (Walsh and Blows, 2009). Even if the direction of selection differs among populations, the pattern of phenotypic divergence might resemble the pattern of genetic covariation among traits more than the pattern of divergent selection if G is highly ill-conditioned, and the genetic variance is low in the directions of selection (Chenoweth et al., 2010).

In this paper, we bring together within a single statistical framework a number of geometrical approaches designed to establish differences in G-matrices among multiple populations. The approaches we consider are restricted to those that establish a change in genetic variance among populations rather than methods that focus on other matrix summary parameters that are not directly related to the response to selection. We integrate all approaches into a Bayesian framework that enables uncertainty to be placed on the estimation of differences among populations, and we provide worked examples for all approaches based on six G-matrices derived from a previously published data set. Finally, in the on-line Supplementary Material, we supply the R code (Dryad repository: doi:10.5061/dryad.g860v) for the programs and matrix manipulations needed to conduct these analyses.

Materials and methods

We develop four specific approaches to the comparison of G-matrices, all of which focus on establishing differences in genetic variance. The methods increase in complexity, from considering the level of genetic variance in random vectors and how these differences among matrices are distributed across the phenotypic space (Method 1), to the identification of higher-dimensional common spaces (Method 2) and ending with two approaches that consider differences in genetic variance across the entire space (Methods 3–4). The first three methods assume no more information is available than the G-matrices themselves, while Method 4 takes advantage of information on the direction of selection when it is known.

Bayesian analyses

We place all four approaches in a Bayesian framework that enables the estimation of uncertainty on the genetic parameters that are estimated. One particularly useful feature of Bayesian approaches for the comparison of G is that the uncertainty in estimates of nuisance parameters (for example, trait and generation means in the analyses presented below) is integrated out of the marginal posterior distributions of the parameters of interest (Gelman et al., 2004). The joint marginal posterior distributions therefore capture the uncertainty in G, but also any uncertainty in the estimates of the nuisance parameters influencing G.

Owing to the complexity of the models required to analyse data typical of evolutionary quantitative genetics studies, the full posterior distribution can often not be derived analytically. In these cases, however, it is possible to use Markov chain Monte Carlo (MCMC) methods to evaluate the posterior distribution (Gelman et al., 2004). Here, the Markov process is used to move the chain from a random starting value to regions of parameter space with greater density, thereby permitting sampling of the joint posterior distribution at each step in MCMC chain. When applied correctly, the combination of MCMC and Bayesian approaches allows us to evaluate the full posterior distribution of the parameters of interest while accounting for the uncertainty introduced by nuisance parameters. Furthermore, because the variation among samples of the marginal posterior distribution captures the uncertainty in estimates of the model parameters, applying any linear transformation (for example, projection of a linear combination through a G) to the samples of the posterior distributions preserves this uncertainty (O’Hara et al., 2008; Ovaskainen et al., 2008). Hence, the uncertainty can be carried forward into new analyses and to provide estimates of confidence for metrics of similarity or dissimilarity among matrices.

A useful characteristic of using MCMC approaches to evaluate the posterior distributions of the model parameters is that the variance components are constrained to be positive, and hence the estimated G matrices will be positive definite. Consequently, the posterior distribution of a variance component cannot be used to test whether the variance component is significantly different from zero. It is therefore important to construct a sensible null model for the hypothesis test of interest. For example, to examine whether an increase in the breeding values of Soay sheep on island of St Kilda reflected positive selection on breeding values, Hadfield et al. (2010) compared the observed temporal trend in breeding values with a null model representing the temporal tend in breeding values under genetic drift alone. Their study demonstrated that, despite the uncertainty in the estimated breeding values (as determined through Bayesian methods), the increase in the average breeding value of the Soay sheep population was greater than the null, and so it is likely that selection rather than drift caused the observed increase in breeding values.

Here, we use a similar approach to compare our observed differences among G-matrices to a null model where we assume the differences among G are driven by random sampling variation alone. Conceptually, our approach is equivalent to the standard approach of estimating null G through the randomisation of individuals (or families) among populations (Roff et al., 2012). The key difference here is that we generate the null G from the posterior predictive distribution of breeding values for the observed G. This approach has several general advantages. First, this approach can be applied across diverse pedigree structures where the unit of randomisation is the individual’s estimated genetic value (Ovaskainen et al., 2008). Second, because the null G are estimated from the posterior predictive distribution of breeding values, the approach has a lower computational requirement than re-running models for each randomised data set. Finally, the procedure ensures that the set of randomised G-matrices have the same structure as the set of observed G-matrices. Consequently, the same matrix comparison metrics can be applied to both the observed and randomised G, allowing hypothesis tests comparing differences in our observed G to a set of null G, based on the assumption that differences are driven by sampling alone.

To generate our randomised G, we first estimate the marginal posterior distribution of G for our six populations of interest (described below). Second, for each MCMC sample, we calculate posterior predictive breeding values for individuals by taking draws from a multivariate normal distribution with a mean of zero and a variance of the ith MCMC sample of the jth G. Importantly, breeding values are assigned using the pedigree corresponding to each population. Finally, we randomly assign individuals to one of six hypothetical populations and construct G-matrices from the vectors of breeding values.

Example data set

The example data set we use is a subset of an experiment reported in Hine et al. (2011), where specific details of the experimental design and laboratory procedures can be found. Briefly, an artificial selection experiment was conducted on eight traits (cuticular hydrocarbons) in Drosophila serrata. There were two treatments (b and m) in which different linear combinations of the eight traits were selected on for 11 generations, with two replicate populations per treatment. Two control (c) populations were also maintained under the same experimental conditions. In both of the treatments, and in the controls, paternal pedigrees were recorded for all males every generation, and the eight traits were recorded for each of these males. Here, we utilised the pedigree and phenotypic data from the final four generations (8–11) to estimate G using an animal model. This yielded a total of six G-matrices for comparison. The G for each population was estimated using the MCMCglmm package (Hadfield, 2010) in R (R Development Core Team, 2013) to fit the model:

where X, Z₁ and Z₂ are the incidence matrices that, respectively, relate the vectors of trait and generation means (b), the vector of additive genetic effects (u₁) and the vector of vial effects (u₂) to the observations in y. The vector e contains the error. MCMCglmm fits mixed models in a Bayesian framework using MCMC to sample the posterior distributions of the location effects and variance components. For the location parameters, priors were normally distributed and diffuse about a mean of zero and a variance of 10⁸. For the variance components, we used weakly informative inverse-Wishart priors with the parameters for the distribution set to 0.001 for the degrees of freedom, and for the scale parameter we defined a diagonal matrix containing values of one third of the phenotypic variance. To assist with model convergence, the response vector (y) was rescaled, with all elements multiplied by 10. The joint posterior distribution was estimated from 1 003 000 MCMC iterations sampled at 100 iteration intervals after an initial burn-in period of 3000 iterations. Overall, model convergence (Geweke as well as Gelman and Rubin diagnostics) and model fit diagnostics (posterior predictive distributions) indicated the MCMC chain sampled the parameter space adequately. Example script to run these models is presented in Dryad (Dryad repository: doi:10.5061/dryad.g860v). The functions for the matrix comparison methods below are presented in the Supplementary material as a tutorial and in Dryad (Dryad repository doi: 10.5061/dryad.g860v).

Method 1. Random projections through G

Random skewers is a method used to compare differences in orientation among G (Cheverud, 1996; Cheverud and Marroig, 2007). In these approaches, random β vectors are placed into the multivariate breeders’ equation with each G, and the vector correlations between the resulting Δ z vectors are used as an indication of the differences among G. The test for the significance of the similarity or dissimilarity of the matrices is then evaluated by comparison of the distribution of observed vector correlations with a distribution of vector correlations conforming to a null model. The null models are often generated by bootstrapping and represent cases where matrices have coincident spaces (vector correlations of∼1) (for example, Calsbeek and Goodnight (2009)), or cases where matrices have distinct spaces (vector correlations of ∼0) (for example. Cheverud and Marroig (2007)), depending on whether researchers are interested in convergence or divergence among G (Roff et al., 2012).

Hansen and Houle (2008) described how, in addition to the differences in Δ z, a random skewer approach can be used to examine differences among G in the magnitude of genetic variance (as well as metrics of variance such as evolvability and respondability) using matrix projection. In this section, we develop an approach based on the projection of random skewers that, when used in combination with estimates of marginal posterior distribution of G, can test for differences in the magnitude of genetic variances. This approach can also be used to describe the trait combinations that differ most often among G. Although we limit our approach here to differences in genetic variance among matrices, it is readily adapted to other scaled measures of variance such as evolvability and respondability.

Each random vector (typically 1000 or more) is projected through each MCMC sample of each G-matrix to generate a posterior distribution of the genetic variance in the direction of the random vector for each population. Differences in genetic variance among populations are then evaluated by examining the overlap of the highest posterior density (HPD) intervals between all possible combinations of populations. All vectors that result in non-overlapping HPD intervals between any pair of populations are then collated, and the product-moment G of the vector elements calculated. This n × n matrix (where n is the number of traits), R, describes which parts of the phenotypic space tend to show significant differences in genetic variance and this part of the space can be further investigated through an eigenanalysis of R. It is important to note that, because the random skewers probe the entire phenotypic space, each significant random skewer (that is, the vectors contributing to the estimation of R) can contain some component of those dimensions that significantly differ, as well as of those that do not. Therefore, to identify which dimensions of R represent genuine differences in genetic variance, we projected the eigenvectors of R back onto both the observed and randomised G-matrices.

Method 2. Krzanowski’s common subspaces

The most basic, and perhaps the most important, question one can ask about multivariate genetic variance is: which part of the trait space has genetic variance, and which part does not? To answer this question, approaches to determining the dimensionality of G have been developed, defining that subspace of G for which there is statistical evidence for the existence of genetic variance (Kirkpatrick and Meyer, 2004; Meyer and Kirkpatrick, 2005; Mezey and Houle, 2005; Hine and Blows, 2006). When multiple populations are present, the identification of which subspace is shared among G is necessarily complicated because of the many different hypotheses that are possible to test. Krzanowski (1979) first described how to establish if the parts of the space that contain ‘most’ of the (genetic) variation are similar between two (G) matrices using:

where the matrices A and B contain a subset k of the eigenvectors of the two G as columns, and where k⩽n/2. The sum of the eigenvalues of S gives a bounded statistic, which ranges between complete orthogonality (0) and complete overlap (k) of the two subspaces, respectively. Blows et al. (2004) give further details on the use of this approach for comparing G-matrices and second-order fitness surfaces.

For more than two populations, the subspace most similar across populations (t=1, …, p) is found using (Krzanowski, 1979):

where A_t contains the subset k_t of the eigenvectors (as columns) of G_t. The first k (k=min(k_i), i=1,…, p) eigenvalues of H can take on a maximum value of p. Any eigenvector of H associated with an eigenvalue equal to p can be reconstructed exactly for a given population from a linear combination of the eigenvectors of G that defined that population’s subspace for the calculation of H. Eigenvalues less than p indicate that at least one population cannot exactly reconstruct the corresponding eigenvector of H from a linear combination of the eigenvectors of G that defined its subspace. For those eigenvalues less than p, we can quantify how close the corresponding eigenvector of H is to each population’s subspace.

The angle (δ) between each eigenvector of H and each of the p population subspaces is given by:

Although Krzanowski’s approach identifies common subspaces based on their orientation, the magnitude of genetic variance contained in even identical subspaces could vary substantially. For instance, differences in total matrix size, or variation among G in eigenvector order could lead to differences among populations in the genetic variance associated with a common subspace. Insight into differences among populations in genetic variance associated with common subspaces can be gained in this context by using projection to find the genetic variance in each population for those b_i that are judged to form part of the common subspace. Statistically significant differences among matrices in the magnitude of the genetic variation in the common space can then be determined using the overlap among HPD intervals.

It is worth noting here the relationship between Krzanowski’s approach, and the more comprehensive hierarchy of common space comparisons developed by Flury (1988). Although Krzanowski’s approach is directed towards determining if those eigenvectors explaining the most variance are similar, the Flury hierarchy imposes no such restriction. For most applications in quantitative genetics, Krzanowski’s approach is likely to have the greater utility for two reasons. First, as shown by equation (1), it is that part of the space of G that contains the most genetic variance that determines the extent of bias in the response to selection, and therefore how differently populations might respond to the same selection regime. Second, the Flury method was developed for product-moment covariance matrices, and hence the degrees of freedom to properly implement the full Flury hierarchy are unknown for all but the most simple of genetic designs requiring variance-component estimation of G. Application of the Flury method to the comparative analysis of G is therefore strictly limited.

Method 3. The genetic covariance tensor

We now describe an approach that is designed to determine how matrices differ without recourse to the random probing of the matrices as in method 1 above. For the simple case of a comparison of two matrices, two similar approaches have been used to determine if the matrices are different. The first is the resultant matrix of the difference, C=A−B; and recently a likelihood ratio tests of the rank of the difference have been developed (Schott, 2010). In the evolutionary literature, the comparison of G-matrices through their difference forms the basis of approaches exploring how much divergence between populations can be caused by uniform linear selection (Hansen and Houle, 2008), and also to assist in identifying dimensions for univariate comparisons of genetic variance (Sztepanacz and Rundle, 2012). The second metric is the resultant matrix of the ratio C=A⁻¹B. This metric forms the basis of the comparisons of phenotypic covariance matrices in the morphometrics literature (Mitteroecker and Bookstein, 2009). For both of these approaches, the leading eigenvectors of the resultant matrix, C, reveal which dimensions differ most between the two matrices, on the absolute scale in the first instance or on the relative scale in the second.

A natural extension of the comparison of two matrices by analysing their difference is the characterization of the variation among multiple matrices with the fourth-order covariance tensor, Σ (Hine et al., 2009). The order of a tensor indicates how many indices are required to reference its elements; for example, vectors and matrices are first and second-order tensors, respectively. A fourth-order tensor is required to describe the variation among multiple matrices. The eigenanalysis of a covariance tensor (discussed in detail below) calculated on two matrices returns the matrix of the difference between two matrices. The elements of Σ represent the variances of, and covariances among, the elements of the multiple covariance matrices:

Obtaining E, the set of second-order eigentensors of Σ, is the first step in exploring the variation among matrices that is summarized by Σ. The eigentensors and eigenvalues of Σ are analogous to the eigenvectors and eigenvalues of a product-moment G in several ways. First, the eigentensors describe independent aspects of variation in covariance structure, the same way eigenvectors describe uncorrelated dimensions of variation in trait space. Second, the original G-matrices can each be expressed as a linear combination of the eigentensors, the same way a given vector can be expressed as a linear combination of eigenvectors. Third, the size of the eigenvalue corresponding to an eigentensor reflects the variation among matrices with respect to how much that eigentensor contributes to their covariance structure. 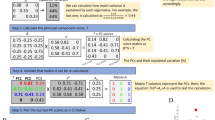Fourth, the maximum number of non-zero eigenvalues of a covariance tensor is equal to the smaller of and p−1, the same way the maximum number of non-zero eigenvalues of a covariance matrix is the smaller of n and the sample size minus one. In practice, the eigentensors of Σ can be obtained by first mapping Σ onto the symmetric matrix S (Figure 1; see Hine et al. (2009) for details). The elements of the ith eigenvector of S can then be scaled and arranged to form E_i.

The next step in exploring the variation among matrices summarized by Σ is to obtain the eigenvectors and eigenvalues of the eigentensors, which can be interpreted in a similar way to those of G. For example, if the largest eigenvalue of an eigentensor is close to 1, the detected change in covariance structure can be attributed to the change in genetic variance in a single trait combination. Unlike a true covariance matrix, eigentensors can have a mix of positive and negative eigenvalues, which will result when a co-ordinated change in genetic variance involves an increase in genetic variance in some trait combinations and a decrease in others.

The Bayesian framework can be utilised to determine which of the independent aspects of genetic covariance structure identified by the tensor exhibit significant variation among populations. First, for the ith MCMC sample of the set of G, we determine the matrix respresentation of the tensor, S_i. Next, we calculate the elements of from the corresponding posterior means of the elements of the set of S_i (i=1 to 10 000). The jth eigenvector of is then projected onto S_i (equivalent to projecting onto Σ) to determine α_ij, the variance among the ith MCMC sample of the G-matrices for the aspect of covariance structure specified by . Projecting an eigentensor onto a tensor is analogous to projecting a vector onto a G-matrix to determine how much variance is present in a particular direction. The posterior distribution of α_j summarizes the uncertainty in the variance in covariance structure represented by . This distribution of α_j is then compared with a distribution of the α_j generated from the null model, where the variation among matrices is due to sampling variation, not biologically meaningful differences.

Method 4. The decomposition of the multivariate breeders’ equation

The approaches discussed so far are generally applicable in the sense that no further biological information is required other than the G themselves. However, in the presence of information on the direction of selection, more specific hypotheses concerning how differences among G bias the response to selection can be addressed. For a single population, equation (1) can be re-written to emphasize the responses of the individual traits. For example, in a two trait analysis, (1) can be written as:

In this form, it can be seen how the ith eigenvector of G (g_i) contributes a proportion of the response for each of the individual traits. The magnitude of this contribution is determined by how close β is to that particular eigenvector, and how large its eigenvalue is. Using this decomposition in an empirical setting, the differences between two populations in their response to the same β can be partitioned into differences as a result of each eigenvector of G.

Uncertainty can be placed on the predicted multivariate response to selection using the genetic covariance between fitness and the metric traits included in the analysis. This approach incorporates uncertainty both in the estimation of G and in the vector of selection gradients β. However, for many biological systems, measures of fitness (and thus the estimates of selection) might typically come from experiments that are independent of the breeding designs used to estimate G. Here, we therefore consider only the situation where uncertainty in the response to selection, and how G influences this response, is a product of uncertainty in G itself and not in β.

For any pair of populations, a difference in overall predicted response for an individual trait can be determined from the comparison of HPD intervals of the linear transformation by β of the posterior samples of G. To determine which eigenvectors of G have contributed to this difference, we use a slightly modified version of equation (1). Here, we substitute λ_i in equation (1) with the genetic variance for each MCMC sample of G in the direction of the eigenvectors of posterior mean G. This allows us to generate the posterior distribution of eigenvector-specific components of the predicted response for each population.

An alternative way to view the effects of differences in G on the response to selection is to focus on the major changes in genetic variance among the G matrices. This can be achieved by using an alternative decomposition of the breeders’ equation that involves the eigentensors of the genetic covariance tensor:

where is the Frobenius inner product of and and reflects the weighting of the ith eigentensor for the jth posterior mean. Then, similar to our modification to equation (1) above, we can generate the posterior distribution of as the set of Frobenius inner products of in each MCMC sample of G_j.