Introduction

The contribution of epistatic interactions to variation of quantitative traits is supported by classical quantitative genetic studies such as generation mean analyses (for example, Mather and Jinks, 1982). Furthermore, epistatic interactions have also been identified in model species as well as various crops using populations of near-isogenic lines (for example, Eshed and Zamir, 1996; Kroymann and Mitchell-Olds, 2005) or linkage mapping populations (for example, Blanc et al., 2006), where differing conclusions about the importance of epistasis have been made in different studies. It has been suggested that this observation might be because of the differing experimental materials used (Eshed and Zamir, 1996). Another explanation might be the difference in the reproduction type of the examined species, as studies in autogamous species have more often provided evidence for the importance of epistasis than studies in allogamous species (Holland, 2001).

Association mapping methods, which use the population-wide linkage disequilibrium (LD), are increasingly being used in order to identify quantitative trait loci (QTL) (for example, Thornsberry et al., 2001; Yan et al., 2010). However, with very few exceptions (for example, Manicacci et al., 2009; Stracke et al., 2009; Li et al., 2010), all earlier association mapping studies have neglected the presence of epistasis. This might be because of the high computational burden of mixed-model association mapping approaches, which to our knowledge are the state of the art for performing association analyses in structured populations (Yu et al., 2006). However, no earlier study examined alternative approaches for detection of epistatic interactions (cf. Aulchenko et al., 2007).

The power to detect marker–phenotype associations is a function of the allele frequency, the sample size, the importance of population structure as well as the extent of LD. Therefore, earlier studies examined, based on empirical data sets, the power of various association mapping approaches with respect to the detection of QTL with additive effects (Yu et al., 2006; Stich and Melchinger, 2009). To our knowledge, however, no earlier study examined the power to detect pairwise epistatic interactions using association mapping methods.

Association mapping approaches are particularly useful for species for which either the development of segregating populations is extremely laborious or where linkage analysis is complicated by polysomic inheritance (Luo et al., 2001). The latter is the case for cultivated potato (Solanum tuberosum). Potato cultivation is strongly affected by the oomycete Phytophthora infestans, which causes the late blight disease. Without chemical control, epidemics of P. infestans can lead to complete yield loss. Extensive use of pesticides in crop protection increases production costs, is damaging to the environment and contributes to the emergence of resistant P. infestans isolates (Duncan, 1999; Kamoun and Smart, 2005). Therefore, we used the resistance of late blight and the correlated trait plant maturity (PM) as model traits for our study in order to contribute to a genetic improvement of potato. To reach this goal, 22 candidate loci, which were selected on the basis of (i) colocalization with known QTL for resistance to P. infestans or other pathogens; (ii) close linkage with R genes or R gene-like sequences and/or (iii) coding for a gene with known function in pathogen resistance, were examined.

The objectives of our research were to (i) compare a classical mixed-model approach with a combined mixed-model and analysis of variance approach for detecting epistatic interactions; (ii) examine with computer simulations the statistical power to detect additive–additive, additive–dominance and dominance–dominance epistatic interactions and (iii) detect epistatic interactions between candidate loci for resistance to leaf blight in a set of tetraploid potato clones.

Materials and methods

Plant materials

Our study was based on 184 tetraploid potato cultivars from the breeding programs of Böhm-Nordkartoffel-Agrarproduktion OHG (Ebstorf, Germany) and SAKA-Pflanzenzucht GbR (Windeby, Germany). The clones were selected to represent a broad range of breeding materials with respect to field resistance to late blight after excluding very late-maturing genotypes. In addition, no full sibs were included in the set. Further details of the germplasm set are described elsewhere (Pajerowska-Mukhtar et al., 2009).

Phenotypic evaluation

The clones of our study were evaluated for field resistance to late blight during the years 2004 to 2006, with two replications per year at one to two locations as described by Pajerowska-Mukhtar et al. (2009). The plots were inoculated with a mixture of two complex field isolates of P. infestans. Disease progress was monitored every 3–4 days, using a 1-to-9 scale (1, 0% infection; 9, >90%), and the area under the disease-progress curve (AUDPC) (Fry, 1978) was calculated for each year–location combination. Furthermore, PM was evaluated in uninfected plants grown under standard phytosanitary regimes in comparison with standard potato varieties of known maturity type, using a 1-to-9 scale (1, very late; 9, very early maturing). From AUDPC and PM, maturity-corrected resistance (MCR) was calculated (Pajerowska-Mukhtar et al., 2009).

Collection of genotypic data

The potato clones of our study were fingerprinted using 31 genome-wide-distributed simple sequence-repeat markers. For 21 markers, the allele dosage was scored based on relative band intensities. Furthermore, 22 candidate loci (Table 1) selected on the basis of (i) colocalization with known QTL for resistance to P. infestans or other pathogens, (ii) close linkage with R genes or R gene-like sequences and/or (iii) coding for a gene with known function in pathogen resistance were custom-sequenced as described previously by Pajerowska-Mukhtar et al. (2009). Single-nucleotide polymorphisms and insertion/deletion polymorphisms (InDels) detected from sequence alignments are designated in the following sections as molecular markers. The single-nucleotide polymorphism allele dosage in heterozygous individuals (1:3, 2:2 or 3:1) was estimated from the height ratio of the overlapping base-calling peaks manually as well as using the data acquisition and analysis software DAx (Van Mierlo Software Consultancy, Eindhoven, the Netherlands). For our study, only such markers were used, which occurred in at least two potato clones.

Table 1 Locus name, description, chromosome location and number of polymorphisms (Polym.) of the candidate loci examined in the current study
Full size table

Statistical analysis

As described by Pajerowska-Mukhtar et al. (2009), an adjusted entry mean M was calculated for each of the 184 potato clones for each of the three examined traits. Furthermore, for each trait, heritability on an entry mean basis was calculated according to the procedure described by Holland et al. (2003).

Population structure analysis

A population structure matrix Q was calculated on the basis of the 31 simple sequence-repeat markers using the software STRUCTURE (Pritchard et al., 2000), which gives for each clone under consideration the probability of membership in each of K subpopulations. In our investigations, the set of 184 clones was analyzed by setting K from 1 to 20 in each of five repetitions. For each run of STRUCTURE, the burn-in time as well as the iteration number for the Markov Chain Monte Carlo algorithm were set to 100 000, following the suggestion of Whitt and Buckler (2003). To determine the most probable value of K, the ad hoc criterion described by Evanno et al. (2005) was used. The K columns of the Q matrix add up to 1 and, thus, only the first K-1 columns were used as an S matrix.

Association analysis

We used a mixed-model approach, which is similar to the QKTopt method described by Stich and Melchinger (2009), for identifying markers in the candidate genes whose additive effects are significantly associated with the trait under consideration:

where Mi is the adjusted entry mean of the ith clone, μ the intercept term, aq the allele substitution effect of the qth molecular marker, xiqa the genotype indicator of the ith clone at the qth molecular marker with respect to the additive effect (xiqa takes one of five values {0, 1, 2, 3, 4} depending on the dosage of one of the two present alleles), vu the effect of the uth column of the population structure matrix S, the total genetic effect of the ith clone except for the fixed effects of the model, and ei the residual. Only the variation modeled by and ei was regarded as random, where it was assumed that and . K was a 184 × 184 matrix of kinship coefficients that define the degree of genetic covariance between all pairs of clones. We calculated the kinship coefficient Kyz between clone y and z on the basis of marker data according to

where Uyz is the proportion of marker loci with shared variants between clone y and z, and T is the conditional probability that marker alleles are alike in state, given that they are not identical by descent. For the examined values T=0, 0.025, …, 0.975, the corresponding matrices KT were obtained and negative kinship values were set to 0. The optimum T value was estimated as descibed by Stich et al. (2008), and the corresponding KT matrix was used as a K matrix. R was a 184 × 184 matrix in which the off-diagonal elements were 0 and the diagonal elements were calculated as the square of the standard errors of the adjusted entry means. Potato clones are highly heterozygous and, thus, was the total genetic variance except the variance explained by the fixed effects included in the model, and was the residual variance, both estimated by REML. In order to identify the n molecular markers with significant additive effects, which were designated in the current study as additive cofactors, the above-described mixed model was used in several runs across all molecular markers similar to a multiple forward regression. For this analysis, a P-to-enter criterion of 0.005 was chosen for the applied Wald-F-test (Searle, 1971), with denominator degrees of freedom approximated by the method of Kenward and Roger (1997).Similarly, we used subsequent runs of the model

where n is the number of additive cofactors; hq1, hq2 and hq3 are the bi-, tri- and tetragenic effects of the qth molecular marker, respectively (Gallais, 2003); and , and are the genotype indicators of the ith clone at the qth molecular marker with respect to the bi-, tri- and tetragenic effects; , and take one of two values {0, 1} depending on whether the clone under consideration belongs to the corresponding heterzygote class (1) or not (0), to identify using a P-to-enter criterion of 0.005 in the Wald-F-test the m molecular markers with significant dominance effects. These m molecular markers were designated in the current study as dominance cofactors. As in the previous model, only variation modeled by and ei was regarded as random.

Two different approaches were applied to identify epistatic interactions. In the mixed-model approach, we performed for all r pairs of molecular markers a Wald-F-test to examine the significance of additive–additive (AA: aa), additive–dominance (AD: ah1, ah2, ah3, h1a, h2a, h3a) or dominance–dominance (DD: h1h1, h1h2, h1h3, h2h1, h2h2, h2h3, h3h1, h3h2, h3h3) epistatic interaction effects using the following model:

where n and m are the number of additive and dominance cofactors, respectively, and , and the incidence vectors relating the genotypic information of the ith clone at the rth pair of molecular markers to AA, AD and DD epistatic interaction effects, respectively. , and were calculated as direct products of the corresponding combinations of xa, , and of the marker pair under consideration. Only variation modeled by and ei was regarded as random.

For the residual approach, which was based on the method proposed by Aulchenko et al. (2007), we used the following model:

to calculate ei, where only variation modeled by and ei was regarded as random. These residuals were then used to examine for all r pairs of molecular markers the significance of AA, AD and DD epistatic interaction effects using the following linear model:

where si is the residual. For those pairs of molecular markers, for which significant epistatic interactions have been observed using the residual approach, the effects of epistatic interactions as well as the proportion of the explained genotypic variance hg2 were calculated using the above-described mixed-model approach (cf. Aulchenko et al., 2007). hg2 was computed in our study based on the relative reduction in when the corresponding terms were added to the model.

In order to compare the distribution of the P-values of the two above-described approaches for identifying epistatic interactions, the mean of squared differences (MSD) between observed and expected P-values was calculated as described by Stich and Melchinger (2009). Multiple testing was considered in our study by using a significance threshold that was derived from computer simulations as described below.

Power simulations

In order to examine the statistical power to detect AA, AD and DD epistatic interaction effects using our data set, the power simulations were based on the genotypic data of the 184 potato clones from which phenotypic data were simulated. We considered one pair of molecular markers for each replication. For each of these two markers, one additional marker was simulated, which has the same allele frequency as the original marker, but shows a predefined level of LD (D′; Lewontin, 1964) to the original marker. The two simulated markers were then used to calculate the genotypic as well as phenotypic values of the 184 potato clones, and the two original markers were used for the test of association. Both procedures will be outlined in detail below.

In each of the three examined scenarios, we assigned the effects of one of the three types of epistatic interactions AA, AD or DD the value 1 (Appendix). Therewith and using the information about the allele configuration present at each of the two simulated loci, we calculated the genotypic value of each of the 184 potato clones. With the variance of the simulated 184 genotypic values σg2 as well as the predefined proportion of the phenotypic variance explained by the epistatic interaction under consideration hp2 (0.01, 0.05, 0.1, 0.15, 0.25, 0.5, 0.75, 1), we calculated for each of the 184 clones a phenotypic value by adding a realization from a normally distributed variable to the genotypic value. Using this procedure, we scale the simulated noise in such a way that the epistatic interaction under consideration explains a predefined level of the phenotypic variance hp2. Owing to the high computational burden of the above-described mixed-model approach, we used only the residual approach for the power simulations. Based on this method we calculated a P-value for the association of the original marker pair and the simulated phenotypic values. This approach was then replicated for all possible molecular marker pairs of the original genotypic data.

In order to calculate the significance level that was used for the power simulations but also for the above-described association analysis of the empirical data, we simulated a random distributed variable and examined for all possible marker pairs the association of their AA, AD and DD effects with the simulated data. This was replicated 100 times. The nominal type-I error rate α was calculated separately for AA, AD and DD as the average of the 1 × 10−6 quantile of the P-values across the 100 replicates. Thereby the empirical type-I error rate α* was set to 1 × 10−6. The statistical power to detect AA, AD or DD epistatic interactions, 1−β*, was calculated as the proportion of marker pairs for which the P-value was lower than α.

All mixed-model calculations were performed using ASReml release 2.0 (Gilmour et al., 2006), whereas all other analyses were performed using the statistical software R (R Development Core Team, 2011).

Results

The heritabilities of the three phenotypic traits assessed for the 184 potato clones ranged from 0.69 for MCR to 0.94 for PM, and was 0.77 for AUDPC. Pearson's correlation coefficient among the adjusted entry means of the three traits varied between −0.03 for PM versus MCR and 0.84 for AUDPC versus MCR, and was 0.50 for AUDPC versus PM.

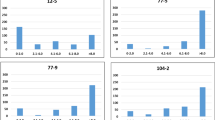
The slopes of the power curves were flat for all three types of epistatic effects for hp2<0.1 or hp2>0.5 (Figure 1), but were steep for 0.1<hp2<0.5. For epistatic interactions with hp2<0.4, the power to detect AA epistatic interactions was higher than that for detection of detect AD or DD interactions, whereas the opposite was true for epistatic interactions with hp2>0.4. The power to detect epistatic interactions, 1−β*, decreased with decreasing extent of LD between molecular markers and the trait-coding loci (Figure 2).

Figure 1
figure 1

Power to detect additive–additive (circles), additive–dominance (triangles) and dominance–dominance (squares) epistatic interactions (1−β*) in the examined set of tetraploid potato clones under the assumption of complete LD between the molecular marker loci and the two corresponding trait-coding loci, which interact epistatically. The empirical type-I error rate α* was 1 × 10−6. hp2 is the proportion of the phenotypic variance explained by the epistatic interaction. LD, linkage disequilbrium.

Full size image
Figure 2
figure 2

Power to detect additive–additive (top), additive–dominance (left) and dominance–dominance (right) epistatic interactions (1−β*) in the examined set of tetraploid potato clones based on an empirical type-I error rate α* of 1 × 10−6, where hp2 is the proportion of the phenotypic variance explained by the epistatic interaction, and D′ the extent of LD between the molecular marker loci and the two corresponding trait-coding loci, which interact epistatically. LD, linkage disequilbrium.

Full size image

The MSD between the observed and expected P-values of the mixed-model approach ranged for the nine examined trait–epistatic effect combinations from 0.0000 to 0.0165 (Table 2). The MSD values for the residual approach were on average slightly lower and varied between 0.0003 and 0.0023. The Spearman's rank correlation coefficients between the P-values of the residual and the mixed-model approach ranged from 0.30 to 0.87, and the Spearman's rank correlation coefficients between the effects of the epistatic interactions were higher and varied between 0.62 and 0.93.

Table 2 MSD between observed and expected P-values for two approaches to identify additive–additive (AA), additive–dominance (AD) and dominance–dominance (DD) epistatic interactions, as well as Spearman's rank correlation coefficient, ρ, between the P-values, as well as the epistatic effects inferred by these two methods for the traits AUDPC and MCR for late blight infection and PM
Full size table

The number of additive cofactors (α=0.005) ranged from 3 (PM) to 5 (MCR), whereas the number of dominance cofactors was lower and varied between 0 (PM) and 2 (AUDPC) (Table 3). The proportion of the genotypic variance explained by all additive cofactors simultaneously varied between 50.8% (MCR) and 74.1% (AUDPC), and between 3.3% (MCR) and 4.5% (AUDPC) for dominance cofactors. The number of significant (α*=1 × 10−6) epistatic interactions was lowest for PM (3) and highest for MCR (32) (Table 4). By contrast, the proportion of the genotypic variance explained by all epistatic interactions simultaneously was lowest for AUDPC (3.6%) and highest for PM (16.5%). For none of the three traits were AA epistatic interactions identified, whereas the number of DD epistatic interactions was highest, with 35 interactions identified. The significant epistatic interactions were not equally distributed across the examined candidate genes (Figure 3). The candidate locus BA81l15t3 showed the highest number of significant (α*=1 × 10−6) epistatic interactions, whereas the candidate loci GP321, St4cl and BA213c14t7 were involved in no significant epistatic interactions.

Table 3 Polymorphisms in candidate loci selected as additive (A) or dominance (D) cofactors (α=0.005) for the three traits examined in our study: AUDPC and MCR for late blight infection and PM
Full size table
Table 4 Polymorphisms in candidate loci significantly (α*=1 × 10−6) associated with their additive–additive (AA), additive–dominance (AD) and dominance–dominance (DD) epistatic interactions with the three traits examined in our study using the residual approach: AUDPC and MCR for late blight infection and PM
Full size table
Figure 3
figure 3

Map of pairwise epistatic interactions for the three traits: AUDPC (red) and MCR (blue) for late blight infection and PM (green). The colored boxes around the names of candidate loci indicate that polymorphisms in the respective candidate genes were selected as additive (solid) or dominance (dashed) cofactors. The arrows between candidate loci indicate that polymorphisms in the genes show significant (α*=1 × 10−6) additive–additive (solid), additive–dominance (dashed) or dominance–dominance (dotted) epistatic interactions using the residual approach. Details of the candidate loci can be found in Table 1. AUDPC, area under the disease-progress curve; MCR, maturity-corrected resistance; PM, plant maturity.

Full size image

Discussion

Comparison of methods for detecting epistatic interactions

One of the objectives of this research was to detect epistatic interactions in a set of tetraploid potato clones. Owing to the fact that the applied genotyping strategy allows the inference of the allele dosage of the examined molecular markers, a two-locus model requires eight main effects as well as 16 epistatic interaction effects. Regarding these markers as fixed in the statistical analyses leads to a reduction of the error degrees of freedom and, thus, a reduction of the power to detect epistatic interactions, 1−β*.

Alternatively, the allele effects and their interactions could be regarded as random and their significance could be assessed using a likelihood ratio test. Association mapping experiments will then examine whether the explained variance of the molecular markers under consideration is 0. The use of likelihood ratio methods for constructing tests for non-zero variance components is a non-standard problem because the null hypothesis that such a variance component is 0 places the true value of the variance parameters on the boundary of the parameter space defined by the alternative hypothesis (Stram and Lee, 1994). Therefore, the likelihood ratio test is in this situation no valid test (Stram and Lee, 1994). This is in accordance with our observation that for an approach with random allele effects the P-values strongly deviated from a uniform distribution (data not shown), which is in accordance with earlier results (Crainiceanu and Ruppert, 2004). Therefore, the allele effects were regarded as fixed in our study.

Mixed-model approaches are currently the method of choice for analysing association mapping experiments (Malosetti et al., 2007). This is because such approaches closely adhere to the nominal type-I error rate in addition to having a high power to detect marker–phenotype associations (for example, Yu et al., 2006). Therefore, in the current study we used a mixed-model approach for detecting epistatic interactions in a set of tetraploid potato clones.

Based on the assumption that only a very small subset of the examined two-way epistatic interactions between the 22 candidate loci are significant, the MSD between observed and expected P-values can be used to evaluate the adherence to the nominal α level (Stich and Melchinger, 2009). The low MSD values observed in our analyses suggested that the mixed-model approach will adhere to the nominal α level (Table 2). However, the drawback of mixed-model approaches is their prolonged computing time (Kang et al., 2008). Nevertheless, any suggestion to reduce the computational burden by limiting statistical testing to only those marker–phenotype associations with significant main effects are probably ill-advised (Phillips, 2008) and, thus, were not followed in our study. This is because epistatic interactions with the largest relative effect size will be those with small main effects. In addition, epistasis is frequently detected in the absence of main effects (Xu and Jia, 2007; Li et al., 2010).

Another way of reducing the computational burden is to use the residual approach instead of a mixed-model approach, which were compared in our study. The mixed-model approach takes about 12 h to examine all two-locus epistatic interactions for one phenotypic trait using an Intel 2.4-GHz Dual Core CPU, whereas the residual approach was considerably faster, taking approximately 20 min. The Spearman's rank correlation coefficient between the P-values of the residual and the mixed-model approach ranged from 0.30 to 0.87 (Table 2). The correlation coefficient between the effects of the epistatic interactions were higher and varied between 0.62 and 0.93. These correlation coefficients were in the range of earlier empirical comparisons of different models for association mapping of QTL with additive effects (Stich and Melchinger, 2009). Furthermore, we observed for six of the examined nine trait–epistatic effect combinations lower MSD values for the residual approach than for the mixed-model approach (Table 2). This finding suggested that the residual approach, in comparison with the mixed-model approach, does not lead to an increased rate of false-positives. Another important criterion to compare different association mapping approaches is the statistical power. Owing to the high computational burden of the mixed-model approach, we were not able to compare both methods with respect to their power to detect epistatic interactions. However, the results of Aulchenko et al. (2007) suggested that the power to detect the marker–phenotype associations of the residual approach was in the worst scenario, with approximately 96% of the power of the mixed-model approach only slightly inferior than the latter. In consideration of these facts, we used for all further analyses the residual approach.

Power simulations for the set of tetraploid potato clones

Information on the power to detect epistatic interactions in an association mapping context is required, on the one hand, for proper interpretation of the findings of association mapping experiments, but also for the design of new experiments. As with the exception of the power to detect QTL by genetic background interactions (Jannink, 2007) this information was lacking, we performed such power simulations in our study. Theoretical considerations suggested that the power to detect epistatic interactions might be influenced by (i) the proportion of the phenotypic variance explained by the epistatic interaction; (ii) the type of epistatic interactions; (iii) the extent of LD between the molecular marker locus and the trait coding locus; and (iv) the population size.

Proportion of the explained phenotypic variance

A higher power 1−β* was observed for scenarios in which the epistatic interactions explained a higher proportion of the phenotypic variance (Figure 1). The relationship between 1−β* and hp2, however, was not linear but rather S-shaped. This observation is in accordance with results from studies on the power to detect QTL with additive (for example, Charcosset and Gallais, 1996) or epistatic effects (for example, Baierl et al., 2006) in linkage mapping populations.

Type of epistatic interactions

The analysis of heterozygous potato clones allows the discrimination between AA, AD and DD epistatic interactions (Cockerham, 1954). The results from our computer simulations suggested that the 1−β* values for epistatic interactions with hp2<0.4 is highest for AA effects and lower for AD and DD effects (Figure 1). This finding is in good accordance with the results of Baierl et al. (2006), who examined hp2 values <0.2 and observed in inter-cross populations that the 1−β* values for AA epistatic interactions were slightly higher than those for the AD or DD epistatic interactions. Nevertheless, no earlier study observed that, for scenarios with hp2>0.4 the 1−β* values were higher for AD and DD than for AA epistatic interactions. This finding requires further research.

Extent of LD between the molecular marker locus and the trait-coding locus

A higher power 1−β* was observed for scenarios with a high extent of LD between the two trait-coding loci and the corresponding molecular markers (Figure 2). This observation is in accordance with results of Kruglyak (1999) on the power to detect markers with main effects in association mapping experiments. Furthermore, we observed that the reduction of the power 1−β* observed for a decreasing level of LD between molecular markers and trait-coding loci was not identical for the different effects of epistatic interactions (Figure 2). This finding might be explained by the factor also responsible for the above-outlined observation that in scenarios with hp2>0.4 the 1−β* values were higher for AD and DD than for AA epistatic interactions. However, the reason for this observation is unclear at the moment.

Population size

Theoretical considerations as well as results from empirical studies on joint linkage and association mapping experiments (Stich et al., 2007) suggest that the power 1−β* can be increased by increasing the sample size. This is because in this case the allele as well as the interaction effects can be estimated more precisely.

However, we also want to advert that using for the detection of epistatic interactions a sample that is considerably smaller than that used in our study will considerably reduce the power 1−β*. In this case, only epistatic interactions explaining a high proportion of the genotypic variance can be detected, which, however, might not exist for the trait under consideration. Therefore, based on our results from computer simulations we recommend to use at least 150 genotypes for the detection of epistatic interactions.

In summary, the results of our computer simulations suggested that, if molecular markers are available, which are in high LD (D′>0.9) with the two trait-coding loci, even epistatic interactions, which explain only 5–10% of the phenotypic variance, can be detected with a power 1−β* of up to 0.2, which seems to be promising for their detection. A high extent of LD between molecular markers and the two trait-coding loci can be expected in association mapping experiments either when using a very high marker density in genome-wide association mapping studies or as in our study by resequencing functional and/or positional candidate loci. Therefore, it seemed promising to detect epistatic interactions in our set of tetraploid potato clones.

Epistatic interactions in the set of tetraploid potato clones

In the current study, we identified for all three traits significant epistatic interactions using the residual approach. The applied significance levels, which were derived from resampling simulations, are expected to result in an empirical type-I error rate of 1 × 10−6. As this significance level is slightly lower than that suggested based on Bonferroni–Holm correction (Holm, 1979), we expect that the proportion of biologically interpretable interactions among the identified epistatic interactions is high.

The number of epistatic interactions identified for the three traits differed considerably and ranged from 3 (PM) to 32 (MCR) (Table 4). The high number of identified epistatic interactions might be explained by the fact that MCR is, in contrast to AUDPC and PM, a meta trait, for which trait values were calculated from the trait values of the other two traits. Therefore, it is expected that MCR has a higher genetic complexity than AUDPC and PM. Another reason for the low number of identified epistatic interactions for PM might be that the candidate loci of this study were selected with respect to their involvement in late blight resistance, but they are no explicit candidates for PM. Therefore, our finding suggested that the candidate loci selection in our study was successful.

Despite our identification of altogether 39 epistatic interactions for the three traits, none of the identified interactions were of the AA type (Table 4). This observation cannot be explained by differences in the significance threshold, as for all three types of epistatic interactions the nominal α level was chosen based on a resampling procedure in such a way that the empirical α* level was 1 × 10−6. The results of the power simulations suggested that, for those hp2 values expected in our experiment (hp2<0.4) the 1−β* was higher for AA than for AD or DD epistatic interactions (Figure 1). These simulations, however, are based on the assumption that the different types of epistatic interactions explain the same proportion of the variance. Owing to the fact that potato is a highly heterozygous species, the frequency of homozygous genotypes is low (cf. Supplementary Material S1) and, thus, the AA epistatic interactions are expected to explain a lower proportion of the variance than the DD epistatic interactions (cf. Falconer and Mackay, 1996). Therefore, the low proportion of the variance explained by the AA epistatic interactions explains the absence of AA epistatic interactions in our study. The same argumentation as for the absence of AA epistatic interactions can be used to explain the lower number of AD than DD epistatic interactions identified (Table 4).

We observed that the explained proportion of the epistatic interactions was considerably lower than that of the main effects (Tables 3 and 4). This finding is in accordance with earlier studies examining QTL mapping experiments (Xu and Jia, 2007) and can be explained by quantitative genetic theory (for example, Falconer and Mackay, 1996). Furthermore, we think that in association mapping studies, another reason might be the selection of candidate loci. In most cases, these genes are selected from molecular biology studies or studies involving mutant screening approaches, which, in turn, are expected to be more powerful in identifying genes with main rather than epistatic effects.

We observed that the epistatic interactions were not uniformly distributed among the 22 loci. The markers in the candidate locus BA81l15t3 showed with markers in eight other candidate loci significant (α*=1 × 10−6) epistatic interaction for MCR (Figure 3). This finding might be explained by the fact that this candidate locus is closely linked to a cluster of resistance gene-like sequences (Rickert et al., 2003).

Despite the fact that the epistatic interactions between the molecular markers identified in our study explain only a relatively low proportion of the genotypic variance as compared with the molecular markers with significant main effects, we expect that this information is of value for most potato breeding programs in temperate climates. The use of this information on the epistatic interactions in marker-assisted breeding programs is expected to facilitate the early identification of individuals carrying specific allele combinations for the three traits examined in our study.