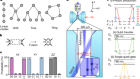
Credit: George M. Bergman/Mathematisches Forschungsinstitut Oberwolfach
In 1994, mathematician Vaughan Jones walked on stage to address the Italian national academy in Rome’s Palazzo Corsini, lit a cigar and began to blow smoke rings. With a mischievous grin, he told the assembled academics, “When I did this in Berkeley, I almost lost my job.”
Jones had little time for the stuffy halls of academia. He cared about the study of knots, a field launched by nineteenth-century physicists experimenting with smoke rings. In 1990, he became the first New Zealander to be awarded the Fields Medal — for an invention that revolutionized the field of topology, the branch of maths that studies knots and other shapes. He attended the solemn ceremony wearing the jersey of New Zealand’s national rugby team. “He was larger than life in many ways, but at the same time he was very humble,” says mathematician Dietmar Bisch at Vanderbilt University in Nashville, Tennessee, a long-time collaborator and friend. Born in 1952, Jones died suddenly on 6 September, aged 67, from complications of an ear infection.
Mathematicians treasure discoveries that reveal links between distant branches of their discipline. Jones’s speciality, operator algebras, provided a powerful tool in the study of knots. His invention, which became known as the Jones polynomial, seeded some of the ideas that physicists later developed into the emerging field of topological quantum computing. Jones’s informal doctoral adviser, Alain Connes, a Fields Medal winner at the Collège de France in Paris, called the discovery “one of the great jewels of the unity of mathematics”.
Jones grew up in Auckland, New Zealand. After studying maths and physics at his local university, he was awarded a scholarship to do his doctorate at the University of Geneva, Switzerland. There he became interested in the theory of operators, which led him to work with Connes, the pre-eminent expert in the field.
Operators are transformations of a space with any number of dimensions — an example being the simple rotations of 3D space. They are central to many areas of maths and to quantum physics, where the geometric properties of operators encode all the possible results of experimental measurements, such as the spectrum of an element’s fluorescent emissions. By the 1970s, Connes had made strides towards a complete classification of particular systems of operators known as Von Neumann algebras. Jones contributed important work towards that goal. One result, now known as the Jones index theorem, showed that when these algebras are nested within one another, their relative sizes conform to precise but enigmatic numerical ratios.
In 1984, while working at the University of Pennsylvania in Philadelphia, Jones came across some formulas that his nested algebras satisfied. These were reminiscent of formulas that appear in the study of braids. Mathematicians study braids as geometric objects, consisting of curved lines twisted around each other. Intrigued, Jones talked to the authority on braids, topologist Joan Birman at Columbia University in New York City. She explained that a braid can be ‘closed up’ end to end, to form a knot. Both researchers began to suspect that Jones’s formulas could be used to generate an expression — a polynomial — that encoded a knot’s properties.
A week later, Jones showed Birman that this was indeed the case. Birman recalls how she realized with astonishment that the ‘Jones poly-nomial’ was a powerful way of telling knots apart. In particular, it could distinguish most knots from their mirror images. It was the kind of tool that topologists had been seeking for decades. Soon, the polynomial and its refinements helped to solve long-standing problems, some of which had been formulated in the late nineteenth century by Peter Guthrie Tait — the smoke-ring pioneer. Researchers also found a plethora of connections between knot theory and physics. Jones investigated connections with statistical mechanics, the study of averaged properties of large numbers of particles.
The most surprising link came in 1989. Theoretical physicist Edward Witten at the Institute for Advanced Study in Princeton, New Jersey, showed that the polynomial can be interpreted as a feature of the quantum physics of a universe with simplified laws of nature and just two dimensions of space. Other theoreticians then found a possible application for Witten’s 2D universes. When electrons are confined to one layer in certain ultracold devices, they can form collective quantum states called anyons. Anyons can ‘remember’ how they have moved around each other, as if they formed braids in space-time. Anyons and similar ‘topological phases’ are now seen as a possible platform for building future quantum computers. They could run quantum algorithms essentially by calculating Jones polynomials.
Jones’s main focus continued to be Von Neumann algebras and their connections to other fields. He introduced a new technique, replacing the expressions of ordinary algebra — symbols arranged linearly — with a 2D graphical arrangement. This planar algebra enabled Jones and others to discover otherwise elusive mathematical relationships.
Jones was a laid-back personality even by the standards of mathematicians. “He was confident in his own powers and had a Southern Hemisphere scorn for social hierarchies,” says his former doctoral student Emily Peters at Loyola University in Chicago, Illinois. He was an avid windsurfer and kite surfer, and frequently organized small conferences in places where participants could also go skiing or hiking. In 2011, he left the University of California, Berkeley, where he had taught since 1985, to join Bisch at Vanderbilt. He was keen to foster mathematics in his native New Zealand, and he spent the first months of every year down south, running a summer school.

 David J. Thouless (1934-2019)
David J. Thouless (1934-2019)
 Shoucheng Zhang (1963–2018)
Shoucheng Zhang (1963–2018)
 John Horton Conway (1937–2020)
John Horton Conway (1937–2020)
 Michael F. Atiyah (1929–2019)
Michael F. Atiyah (1929–2019)
 Maryam Mirzakhani (1977–2017)
Maryam Mirzakhani (1977–2017)