- NEWS AND VIEWS
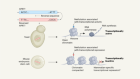
A universal control system for synthetic gene networks
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Rent or buy this article
Prices vary by article type
from$1.95
to$39.95
Prices may be subject to local taxes which are calculated during checkout
Nature 570, 452-453 (2019)
doi: https://doi.org/10.1038/d41586-019-01772-9
References
Aoki, S. K. et al. Nature 570, 533–537 (2019).
Briat, C., Gupta, A. & Khammash, M. Cell Syst. 2, 15–26 (2016).
Olsman, N., Xiao , F. & Doyle, J. C. iScience 14, 277–291 (2019).
Hilfinger, A., Norman, T. M., Vinnicombe, G. & Paulsson, J. Phys. Rev. Lett. 116, 058101 (2016).
Briat, C., Gupta, A. & Khammash, M. J. R. Soc. Interface 15, 20180079 (2018).

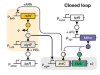 Read the paper: A universal biomolecular integral feedback controller for robust perfect adaptation
Read the paper: A universal biomolecular integral feedback controller for robust perfect adaptation
 Construction of an Escherichia coli genome with fewer codons sets records
Construction of an Escherichia coli genome with fewer codons sets records
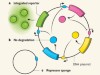 Precision timing in a cell
Precision timing in a cell