The electronic properties of graphene and carbon nanotubes

Abstract

A brief review is given on the characteristic features of electronic states and transport in graphene consisting of a single sheet of graphite, and its cylinder form called a carbon nanotube. Electron motion in graphene is equivalent to that of a neutrino or a relativistic Dirac electron with vanishing rest mass. This causes the appearance of a nontrivial Berry’s phase under 2π rotation in wave-vector space, leading to the absence of backscattering and in the metallic carbon nanotube resulting in perfect conduction even in the presence of scatterers. The energy bands in carbon nanotubes are determined by periodic boundary conditions with a fictitious Aharonov-Bohm flux determined uniquely by the circumferential chiral vector. A nanotube becomes metallic when the flux vanishes and semiconducting when the flux is nonzero. The conductivity of graphene is essentially independent of the Fermi energy and the electron concentration as long as variations in effective scattering strength are neglected, and therefore graphene should be regarded as a metal rather than a zero-gap semiconductor. Various schemes are now being proposed and tested for the purpose of opening the band gap in graphene.

Main

The best known carbon crystal is diamond, whose hardness and high dispersion of light make it useful for industrial applications and jewelry. Under ambient pressures and at room temperature, however, the most stable form of carbon is graphite, which is used as an industrial lubricant and as the ‘lead’ in pencils. Graphite is a layered material in which each layer consists of a sheet of carbon atoms forming hexagonal structures similar to benzene rings. A monolayer of graphite is called graphene, and a carbon nanotube is a cylinder made of graphene.

Carbon nanotubes were discovered by Sumio Iijima during the synthesis of fullerene C₆₀ in 1991. A nanotube exhibits extraordinary mechanical properties that make it ideal for reinforced composites: it has a huge Young modulus, is as stiff as diamond and the estimated tensile strength is more than ten times that of steel wire with the same weight. It has even been suggested that nanotubes could be used to build a ‘space elevator’, an earth-to-space cable. Nanotubes can be metallic or semiconducting, and offer many possibilities for creating future nanoelectronics devices, circuits and computers.

There have been various efforts world over to prepare thin layers of graphite, and quite recently the group of Andre Geim and Kostia Novoselov of Manchester University succeeded in fabricating a field-effect transistor (FET) made of graphene on an Si/SiO₂ substrate.^1,2 They simply stuck a flake of graphite debris onto plastic adhesive tape, folded the sticky side of the tape over the flake, and then pulled the tape apart, cleaving the flake into two. After repetition of the process, the resulting fragments grew thinner and some of them turned out to be monolayer graphene. The concentrations of electrons (n_s > 0) and holes (n_s < 0) can be controlled by the gate voltage between the graphene layer and the heavily doped silicon, through insulating SiO₂, over a wide range of –5×10¹³ < n_s < 5×10¹³ cm^–2.

It is quite amazing that carriers in a thin atomic layer can be controlled almost freely by a gate and that the maximum carrier concentration is comparable to that in silicon-based metal-oxide semiconductor FETs (MOSFETs). Graphene can also be synthesized epitaxially on silicon carbide, by which the silicon leaves the surface and the remaining carbon reconstructs into graphene layers when heated.^3,4 Such epitaxial graphene is much more suitable for actual device applications. Monolayer graphene has been formed on metal surfaces such as nickel, and its phonon properties have been measured.⁵

Two reports were published in Nature by groups from Manchester University and Columbia University in October 2005 on the observation of the integer quantum Hall effect.^6,7 This effect is sometimes called the half-integer quantum Hall effect because the Hall conductivity is quantized into (4e²/h)(j + 1/2), where e is electron charge, h is the Planck constant and j is an integer.⁸ Since those reports, graphene has become the subject of extensive and very competitive theoretical and experimental study. Some examples include reports on interband magneto-optical absorption⁹, cyclotron resonance absorption,^10,11 observation of the local density of states using a scanning single-electron transistor,¹² measurement of weak-field magnetoresistance,^13–16 observation of optical phonons by Raman experiments,^17,18 observation of spin transport,^19,20 angle-resolved photoemission spectroscopy^21,22 and observation of the lattice by scanning tunneling microscopy.²³

There have been a tremendous number of theoretical works on graphene, including a proposal for an ‘electron lens’ by attaching an extra top gate to realize negative refractive index at the p–n junction.²⁴ Extensive literature on graphene research has been covered in recently published reviews.^25–27 Graphene was the subject of theoretical study prior to experimental realizations because the peculiar electronic structure is also responsible for the intriguing properties of carbon nanotubes.²⁸

The two-dimensional neutrino

Graphene has a honeycomb lattice structure and a unit cell that contains two carbon atoms (Figure 1). An electron in a solid sometimes behaves as a particle quite different from that in a vacuum because of the presence of a periodic atomic potential. Graphene is an extremely interesting example of such a case, where the electron motion becomes equivalent to that of a massless neutrino.

Figure 1

The honeycomb lattice of graphene. The hexagonal unit cell contains two carbon atoms (A and B). The chiral vector determining the structure of a carbon nanotube is given by L, and its length gives the circumference. The chiral angle is denoted by η, with η = 0 corresponding to zigzag nanotubes and η = π/6 to armchair nanotubes.

Figure 2 shows the band structure of graphene near the Fermi level. In the hexagonal first Brillouin zone (the primitive unit cell in wave-vector space), the Fermi level lies at the crossing point between the cone-like dispersions (Figures 2(a) and (b)). Given the wave vector k measured from one of these points (K in the figure), the energy is determined by ε(k) = ±ħv|k| = ±v|p| for small k = |k|, where ħ is the reduced Planck constant, p = ħ k is momentum and v is the velocity of the order c/300 with c being the light velocity. According to the special theory of relativity, the energy of a relativistic particle is given by

(1) where m is rest mass. When we set m = 0, this gives dispersion ε = c|p| equivalent to that of light. This particle is a massless neutrino and the negative energy corresponds to an antineutrino. The dispersion of an electron in graphene is obtained by replacing c with v in this equation.

Figure 2

(a) Energy bands near the Fermi level in graphene. The conduction and valence bands cross at points K and K′. (b) Conic energy bands in the vicinity of the K and K′ points. (c) Density of states near the Fermi level with Fermi energy E_F.

The corresponding Schrödinger equation is given by a set of first-order differential equations,²⁸ as follows.

(2)

Here, and F_A(r) and F_B(r) represent the wave amplitude at the A and B sublattice points (as shown in Figure 1). A similar discussion holds for the adjacent K′ point. Thus, the two-dimensional electron system in graphene makes it possible to study the properties of highly relativistic particles.

One intriguing feature of the neutrino wave function is the appearance of a Berry’s phase. When the direction of particle motion is rotated by 2π, the phase of the wave function changes by ±π, changing its sign. This leads to the absence of backscattering when a particle is scattered by impurities, because backscattering corresponds to rotation of the direction by ±π and the amplitudes for ±π rotations cancel each other due to the sign difference.^29,30 In carbon nanotubes, the electron motion along the circumference is quantized and the electron motion effectively becomes one-dimensional, with the resistance determined solely by backscattering. Therefore, the absence of backscattering means that metallic carbon nanotubes are ideal conductors with perfect conduction even in the presence of scatterers.

Carbon nanotubes as either a metal or semiconductor

Let us introduce lattice translation vector L. A nanotube can be constructed in such a way that the hexagon at a position L can be rolled onto a hexagon at the origin. L is called the chiral vector and becomes the circumference of the nanotube. The directional angle η of L is called the chiral angle (Figure 1). Because each translation vector is written as L = n_aa + n_bb with a and b being the primitive translation vectors, the structure of a nanotube is specified by the set of integers n_a and n_b. The axis is perpendicular to L, which typically results in a nanotube with a helical structure. There are some exceptions to this, including nonhelical nanotubes, zigzag nanotubes with η = 0 and armchair tubes with η = π/6. Other helical tubes are called chiral nanotubes. Because the stability is mainly determined by their thickness or circumference, the direction of L for grown nanotubes is distributed almost uniformly.

The wave function satisfies the periodic boundary condition ψ(r + L) = ψ(r) in a carbon nanotube. This shows that the wave vector k satisfying the condition exp[i k·(r + L)] = exp(i k·r) is allowed in the first Brillouin zone of graphene. The condition can be rewritten as exp(i k·L) = 1, which gives straight lines perpendicular to L with neighboring distances 2π/L (Figure 3). When these lines pass through the K and K′ points, that is, exp(i K·L) = 1 or exp(i K′·L) = 1 with K and K′ being the wave vector of the K and K′ point, respectively, there is no gap at the Fermi level and the nanotube becomes metallic. In other cases, the nanotube becomes a semiconductor with a gap near the Fermi level.

Figure 3

Equi-energy lines of the valence band in wave-vector space. The hexagon denotes the first Brillouin zone, L is the chiral vector and η is the chiral angle. Dashed lines denote allowed wave vectors when graphene is rolled into a cylinder to form a carbon nanotube, and show the orientation perpendicular to L. The K and K′ points lie on the dashed lines in metallic carbon nanotubes (a), and lie away from the dashed lines in semiconducting nanotubes (b).

Explicit calculations show that exp(i K·L) = exp(2πiν/3) and exp(i K′·L) = exp(–2πiν/3), where the integer ν is 0 or ±1 depending on n_a and n_b. As a result, metallic (ν = 0) and semiconducting (ν = ±1) nanotubes appear at a ratio of one to two with varying L. In a semiconducting nanotube, the straight line closest to the K or K′ point gives the conduction and valence bands. Because the spacing between neighboring lines is 2π/L and the energy is a linear function of the wave vector near the K and K′ points, the energy gap is proportional to the inverse of the diameter d = L/π. The important feature is that there can be both metallic and semiconducting nanotubes with similar diameter and therefore one of the tough challenges lies in achieving the selective growth of semiconducting and metallic nanotubes or their separation after growth.

Graphene as a metal

Graphene has often been called a zero-gap semiconductor because the density of states is given by D(E) = |E|/2πħ²v², which vanishes at E = 0 (Figure 2). This naming is quite inappropriate, however. A more appropriate name becomes clear when we consider the conductivity of graphene.

The conductivity is usually given by the Einstein relation σ₀ = g_vg_se²D^*D(E_F) in terms of the diffusion coefficient D^*, where g_v = 2 is the valley degeneracy corresponding to the presence of the K and K′ points and g_s = 2 is the spin degeneracy. Let τ be the relaxation time due to impurity scattering. Then, the diffusion coefficient is given by D^* ≈ v²τ. We have τ^–1 ≈ (2π/ħ)n_i〈 u_i²〉 E_FD(E_F), where n_i is the impurity density, u_i is the matrix element of the impurity potential between initial and final states, and 〈…〉 E_F denotes the average at the Fermi level. As a result, independent of the density of states, the conductivity becomes σ₀ = g_vg_se²/2π²ħW, where W = n_i〈 u_i²〉 E_F/4π²ħ²v² is a dimensionless parameter characterizing the strength of impurity scattering. Strictly speaking, the relaxation time determining the conductivity is different from the simple scattering time, but the difference is not so important here.

The above shows that the conductivity is independent of the Fermi energy and the carrier concentration as long as the possible dependence of scattering strength W on E_F or n_s is neglected. Therefore, graphene should strictly be regarded as a metal rather than a semiconductor.

At E_F = 0, where D(E_F) = 0, however, this description can become inappropriate. In fact, potential fluctuations due to impurities make the density of states at E_F = 0 nonzero. Theoretical calculations including this level-broadening effect performed prior to experiments showed that the conductivity takes a universal value of σ_min = g_vg_se²/2π²ħ at E_F = 0.³¹Figure 4 shows examples of calculated density of states and conductivity. In graphene with weak disorder, that is, W ≪ 1, the conductivity drops to σ_min from σ₀ in a very narrow energy range close to E = 0. Similar calculations performed for the conductivity in magnetic fields predicted that the Hall conductivity, in particular, is quantized into (4e²/h)(j + 1/2) with integer j, corresponding to the half-integer quantum Hall effect.⁸

Figure 4

Examples of (a) the density of states and (b) the conductivity of a graphene monolayer calculated by a self-consistent Born approximation. Here, ε₀ is an arbitrary energy unit and ε_c is the cutoff energy corresponding to half of the π-band width. The conductivity exhibits a sharp jump in the limit of weak scattering (W ≪ 1) from the Boltzmann result σ0 for E_F ≠ 0 down to σ = e²/π2ħ at E_F = 0. Figure modified after Ref. 31.

Experimentally, the minimum conductivity has been shown to be nearly independent of samples,⁶ although the absolute value seems to be 3–4 times larger than the theoretical predictions. In the vicinity of zero energy, because of the weak screening effect due to the small density of states and the small kinetic energy of electrons, the effective scattering strength can be substantial and system inhomogeneity can also be significant. Some reports have shown that the minimum conductivity varies from sample to sample.³² This problem regarding the minimum conductivity remains an important subject to be understood in the future.

Another important difference lies in the dependence of the conductivity on electron concentration. The theory predicts that the conductivity in pure graphene should be independent of the electron concentration, dropping to σ_min in the extreme vicinity of zero energy over a singularly narrow region. Experimentally, however, the conductivity is nearly proportional to the electron concentration, as if there is an effective mobility independent of the electron concentration. Part of the reason for this lies in the fact that the scattering strength W is large at E_F ≈ 0 (typically W ≈ 0.1), as mentioned above. Another reason is that the effective strength of dominant scatterers depends on the electron concentration according to W ∝ |n_s|^–1, and the Boltzmann conductivity becomes proportional to the electron concentration.

Typical examples of such scatterers causing n_s dependence are charged impurities. Charged centers localized in SiO₂ are known to play important roles in silicon MOSFETs.³³ Explicit calculations for charged-impurity scattering with the screening effect properly included give W ∝ |n_s|^–1, that is, σ ≈ e|n_s|μ with mobility μ ∝ n independent of n_s.^34,35 The typical mobility in graphene on an SiO₂ substrate is μ ≈ 10⁴ cm²/V s, and the required impurity concentration is n i ≈ 5×10¹¹ cm^–2, comparable to that in a MOSFET.

Singular behavior also appears in the dynamical conductivity, which consists of the Drude conductivity (determined by states in the vicinity of the Fermi level) and the interband conductivity (dominant for ħω > 2|E_F|). The interband conductivity, corresponding to optical transitions from valence to conduction band states, is given by a universal value of g_vg_se²/16ħ. Explicit calculations show that the frequency dependence is completely scaled by the Fermi energy if level-broadening effects are completely neglected, that is, σ(ω,E_F) = σ(ħω/|E_F|) (Figure 5). This shows that at E_F = 0, σ(ω) = σ₀ for ω = 0 and σ(ω) = g_vg_se²/16ħ for ω = 0. It has been shown that this singularity present at E_F = 0 can be removed by level-broadening effects (Figure 5).³⁶ Quite recently, dynamical conductivity was actually observed, demonstrating the universality of interband conductivity.^37,38

Figure 5

(a) Dynamical conductivity obtained by neglecting the level-broadening effect. The frequency dependence is scaled by E_F. (b) Dynamical conductivity calculated including the level-broadening effect. Deviation from E_F scaling appears for small ω and small E_F. Figure modified after Ref. 36.

Opening the band gap in graphene

One of the most important challenges toward achieving graphene-based transistor applications arises from the fact that graphene is not a semiconductor but a metal. Because of the dependence of W on n_s, the conductivity changes as a function of the electron concentration proportional to the gate voltage. In fact, the conductivity in graphene fabricated on an SiO₂ substrate changes from σ_min at E_F = 0 to values 20–30 times larger by the gate. This amount of change is certainly not sufficient for transistors, and further the gate-voltage range corresponding to σ_min is too narrow. There have been various attempts to introduce a band gap for the purpose of converting graphene into a semiconductor.

Let us consider a fictitious case in which the A and B sublattice atoms have different energies: +δ for A atoms and –δ for B atoms. In this case, the energy bands are defined by

(3)

instead of ε_±(k) = ±ħv|k|. This shows that a gap of 2|δ| opens up at k = 0. Such a difference in the energy of the A and B atoms can be realized by growing graphene on an appropriately chosen substrate giving rise to asymmetry between two sublattices.

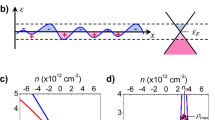
In usual semiconductors, the band gap is enhanced by the increase in kinetic energy of conduction electrons and valence holes when spatially confined to quantum wells or quantum wires. Given effective masses of electrons and holes m_e and m_h, the effective gap increases by (ħπ²/2d²)(m_e^–1 + m_h^–1), where d is the well width. Figure 6 shows a schematic illustration of this enhancement. In graphene also, a gap can be formed when electrons and holes are confined to a narrow region.

Figure 6

Schematic illustration of the enhancement of the effective gap caused by the confinement of conduction electrons and valence holes in a semiconductor quantum well.

It should be noted that spatial confinement cannot be achieved by applying an external potential. In fact, an electron incident perpendicularly on a barrier potential transmits through the barrier with a probability of unity because of the absence of backscattering as mentioned above. The confinement can be achieved only by cutting graphene into a ribbon with narrow width.

In usual semiconductors, the electron motion is described by an effective-mass approximation characterized by a second-order differential equation. In this case, the wave function has vanishingly small amplitude at the boundary (Figure 6) and therefore electrons are only weakly affected by disorder present at the boundary, such as weak boundary roughness scattering. In graphene, however, the Schrödinger equation is given by a set of first-order differential equations and therefore the condition that the wave functions vanish there cannot be imposed. As a result, the amplitudes of the wave functions are almost the same at the edges as on the inside of a graphene ribbon, demonstrating that the electronic states in graphene ribbon are quite sensitive to the edge structure.

The sensitivity to edges has previously been demonstrated through explicit calculations of the electronic states in ribbons.^39,40 In fact, in zigzag ribbons having an edge with a zigzag form, there exist edge states without dispersion, localized in the vicinity of edges. Armchair ribbons having an edge with an armchair form, on the other hand, alternate periodically with width between metallic and semiconducting behaviors, quite analogous to the behavior in carbon nanotubes. The edges of ribbons fabricated by conventional lithography techniques are extensively damaged and therefore far from ideal. Measurements of the conductance of narrow ribbons at various temperatures have indicated that the gap is roughly proportional to the reciprocal of the width.^41,42 It has also been found that the gap is independent of the ribbon direction, and that the conductance decreases considerably with decreasing ribbon width, suggesting that the gap is likely to be a mobility gap related to edge disorder rather than a band gap. The presence of a band gap has been suggested in chemically derived ribbons.⁴³

Multi-layer graphene, such as bilayer and trilayer forms, have also been fabricated. In bilayer graphene in particular, the electronic states become quite different from those in monolayer graphene due to strong interlayer interactions. The dispersion in the vicinity of the Fermi level changes from ε_±(k) = ±ħν|k| in the monolayer to ε_±(k) = ±ħ²k²/2m^* in the bilayer, where m is the effective mass.⁴⁴ In multi-layer graphene, the Hamiltonian has been shown to be generally decomposable into that of monolayer graphene and those of bilayer graphene when only the dominant terms in interlayer interactions are considered.^45,46

When a strong electric field is applied perpendicular to bilayer graphene (Figure 7), the induced potential difference between the two layers gives rise to a band gap of the order of the potential difference. The actual difference is determined in a self-consistent manner because it also leads to asymmetry in the electron density distribution^47,48. This corresponds to the screening of external potential and tends to reduce the gap by roughly half.^47,49 Some examples of calculated potential difference are shown in Figure 7(b).⁴⁹ Several experiments have been reported, including some giving a small band gap⁵⁰ and others suggesting the opening of a huge gap.

Figure 7

(a) Schematic illustration of bilayer graphene with a bottom gate controlling the carrier concentration and an extra top gate. The distance between layers 1 and 2 is d ≈ 0.334 nm, and the potential difference is determined from eFd. F_ext represents the field due to the top gate. (b) Calculated energy difference eFd as a function of electron concentration with respect to eF_extd. The static dielectric constant of the environment is κ = 2. Here, n_s = g_vg_sΔ2/2πħ2v2 ≈ 2.5×10¹³ cm^–2 for interlayer coupling of Δ ≈ 0.4 eV. Figure modified after Ref. 49.

Summary

The characteristic features of the electronic and transport properties of graphene and carbon nanotubes were discussed from a theoretical point of view. An electron in graphene is equivalent to a massless neutrino in two dimensions, and graphene therefore effectively realizes a system of relativistic particles moving with light velocity. The actual velocity is equivalent to about 1/300 of the light velocity. This leads to unique electronic and transport properties in graphene and carbon nanotubes, such as the absence of backscattering, which causes metallic carbon nanotubes to behave as perfect conductors even in the presence of scatterers. Graphene and nanotubes will continue to attract attention because of their considerable potential for device applications as well as their purely scientific interest.