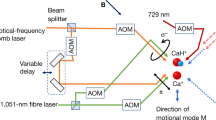
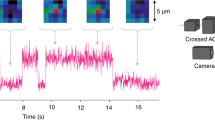
Abstract
Quantum information processors exploit the quantum features of superposition and entanglement for applications not possible in classical devices, offering the potential for significant improvements in the communication and processing of information. Experimental realization of large-scale quantum information processors remains a long-term vision, as the required nearly pure quantum behaviour is observed only in exotic hardware such as individual laser-cooled atoms and isolated photons. But recent theoretical and experimental advances suggest that cold atoms and individual photons may lead the way towards bigger and better quantum information processors, effectively building mesoscopic versions of 'Schrödinger's cat' from the bottom up.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout








Similar content being viewed by others
References
Shannon, C. E. A mathematical theory of communication. Bell Syst. Tech. J. 27, 379–423; 623–656 (1948).
Benioff, P. The computer as a physical system: a microscopic quantum mechanical model of computers as represented by Turing machines. J. Stat. Phys. 22, 563–591 (1980).
Benioff, P. Quantum mechanical Hamiltonian models of Turing machines that dissipate no energy. Phys. Rev. Lett. 48, 1581–1585 (1982).
Feynman, R. Simulating physics with computers. J. Theor. Phys. 21, 467–488 (1982).
Feynman, R. P. There's plenty of room at the bottom. Eng. Sci. February 1960 issue (produced by the CalTech Office of Public Relations) (1960); also available at 〈http://www.zyvex.com/nanotech/feynman.html〉.
Landauer, R. in Proc. Drexel-4 Symp. Quantum Nonintegrability (eds Feng, D. H. & Hu, B.-L.) 44–53 (International Press, Boston, 1997).
Jozsa, R. in The Geometric Universe (ed. Huggett, S. et al.) 369–379 (Oxford Univ. Press, Oxford, 1998); preprint quant-ph/9707034 (Entanglement and quantum computation) at http://xxx.lanl.gov (1997).
DiVincenzo, D. The physical implementation of quantum computation. Fortschr. Phys. 48, 771–783 (2000).
Special issue on experimental proposals for quantum computation. Fortschr. Phys. 48 (2000).
DiVincenzo, D. Two-bit gates are universal for quantum computation. Phys. Rev. A 51, 1015–1022 (1995).
Lloyd, S. Almost any quantum logic gate is universal. Phys. Rev. Lett. 75, 346–349 (1995).
Einstein, A. Podolsky, B. & Rosen, N. Can quantum-mechanical description of reality be considered complete? Phys. Rev. 47, 777–780 (1935).
Kahn, D. The Codebreakers: The Story of Secret Writing (Macmillan, New York, 1967).
Bennett, C. & Brassard, G. Quantum cryptography: public key distribution and coin tossing. Proc. IEEE Int. Conf. Comp. Syst. Signal Proc. 11, 175–179 (1984).
Wiesner, S. Conjugate coding. Sigact News 15, 78–88 (1983).
Bennett, C. Quantum cryptography using any two nonorthogonal states. Phys. Rev. Lett. 68, 3121–2124 (1992).
Franson, J. & Ilves, H. Quantum cryptography using optical fibers. Appl. Opt. 33, 2949–2954 (1994).
Marand, C. & Townsend, P. Quantum key distribution over distances as long as 30 km. Opt. Lett. 20, 1695–1697 (1995).
Muller, A., Zbinden, H. & Gisin, N. Quantum cryptography over 23 km in installed under-lake telecom fiber. Europhys. Lett. 33, 335–339 (1996).
Hughes, R. J., Morgan, G. L. & Peterson, C. G. Quantum key distribution over a 48km optical fibre network. J. Mod. Opt. 47, 533–547 (2000).
Ekert, A. K. Quantum cryptography based on Bell's theorem. Phys. Rev. Lett. 67, 661–663 (1991).
Jennewein, T., Simon, C., Weihs, G., Weinfurter, H. & Zeilinger, A. Quantum cryptography with entangled photons. Phys. Rev. Lett. 84, 4729–4732 (2000).
Naik, D. S., Peterson, C. G., White, A. G., Berglund, A. J. & Kwiat, P. G. Entangled state quantum cryptography: eavesdropping on the Ekert protocol. Phys. Rev. Lett. 84, 4733–4736 (2000).
Tittel, W., Brendel, J., Zbinden, H. & Gisin, N. Quantum cryptography using entangled photons in energy-time Bell states. Phys. Rev. Lett. 84, 4737–4740 (2000).
Kwiat, P. G., Waks, E., White, A. G., Appelbaum, I. & Eberhard, P. H. Ultrabright source of polarization-entangled photons. Phys. Rev. A 60, 773–776 (1999).
Bennett, C. H. et al. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 70, 1895–1899 (1993).
Braunstein, S. L. A fun talk on teleportation. 〈http://www.informatics.bangor.ac.uk/~schmuel/tport.html〉 (5 February 1995).
Bouwmeester, D. et al. Experimental quantum teleportation. Nature 390, 575–579 (1997).
Boschi, D., Branca, S., De Martini, F., Hardy, L. & Popescu, S. Experimental realization of teleporting an unknown pure quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 80, 1121–1125 (1998).
Braunstein, S. L. & Kimble, H. J. A posteriori teleportation. Nature 394, 840–841 (1998).
Bouwmeester, D. et al. Reply to 'A posteriori teleportation' by S. L. Braunstein and H. J. Kimble. Nature 394, 841 (1998).
Furusawa, A. et al. Unconditional quantum teleportation. Science 282, 706–709 (1998).
Schrödinger, E. The present situation in quantum mechanics. Naturwissenschaften 23, 807–812; 823–828; 844–849 (1935).
Deutsch, D. Quantum theory, the Church-Turing principle and the universal quantum computer. Proc. R. Soc. Lond. A 400, 97–117 (1985).
Shor, P. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J. Comp. 26, 1484–1509 (1997).
Rivest, R., Shamir, A. & Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. Assoc. Comput. Mach. 21, 120–126 (1978).
Grover, L. Quantum mechanics helps in searching for a needle in a haystack. Phys. Rev. Lett. 79, 325–328 (1997).
Shor, P. Scheme for reducing decoherence in quantum computer memory. Phys. Rev. A 52, 2493–2496 (1995).
Steane, A. Error correcting codes in quantum theory. Phys. Rev. Lett. 77, 793–797 (1996).
Preskill, J. Battling decoherence: the fault-tolerant quantum computer. Phys. Today 52, 24–30 (1999).
Cirac, I. & Zoller, P. Quantum computations with cold trapped ions. Phys. Rev. Lett. 74, 4091–4094 (1995).
Steane, A. The ion trap quantum information processor. Appl. Phys. B 64, 623–642 (1997).
Wineland, D. et al. Experimental issues in coherent quantum manipulation of trapped atomic ions. J. Res. Natl Inst. Stand. Tech. 103, 259–328 (1998).
Sørensen, A. & Mølmer, K. Quantum computation with ions in thermal motion. Phys. Rev. Lett. 82, 1971–1975 (1999).
Blatt, R. & Zoller, P. Quantum jumps in atomic systems. Eur. J. Phys. 9, 250 (1988).
Monroe, C., Meekhof, D. M., King, B. E., Itano, W. M. & Wineland, D. J. Demonstration of a universal quantum logic gate. Phys. Rev. Lett. 75, 4714–4717 (1995).
Sackett, C. et al. Experimental entanglement of four particles. Nature 404, 256–259 (2000).
Turchette, Q. A. et al. Heating of trapped ions from the quantum ground state. Phys. Rev. A 61, 063418-1–063418-8 (2000).
Larson, D. J. et al. Sympathetic cooling of trapped ions: a laser-cooled two-species nonneutral ion plasma. Phys. Rev. Lett 57, 70 (1986).
Kielpinski, D. et al. Sympathetic cooling of trapped ions for quantum logic. Phys. Rev. A 61, 032310-1–032310-8 (2000).
Morigi, G. & Walther, H. Two-species Coulomb chains for quantum information. Eur. Phys. J. D 13, 261–269 (2001).
Jessen, P. & Deutsch, I. Optical lattices. Adv. At. Mol. Opt. Phys. 37, 95–138 (1996).
Hamann, S. et al. Resolved-sideband Raman cooling to the ground state of an optical lattice. Phys. Rev. Lett. 80, 4149–4152 (1998).
Vuletic, V., Chin, C., Kerman, A. J. & Chu, S. Raman sideband cooling of trapped cesium atoms at very high densities. Phys. Rev. Lett. 81, 5768–5771 (1998).
Perrin, H., Kuhn, A., Bouchoule, I. & Salomon, C. Sideband cooling of neutral atoms in a far-detuned optical lattice. Europhys. Lett. 42, 395–400 (1998).
Raithel, G., Phillips, W. D. & Rolston, S. L. Coherence decay of wave-packets in optical lattices. Phys. Rev. Lett. 81, 3615 (1998).
Haycock, D.L., Alsing, P. M., Grondalski, J., Deutsch, I. H. & Jessen, P. S. Mesoscopic quantum coherence in an optical lattice. Phys. Rev. Lett. 85, 3365 (2000).
Brennen, G., Caves, C., Jessen, P. & Deutsch, I. Quantum logic gates in optical lattices. Phys. Rev. Lett. 82, 1060–1063 (1999).
Jaksch, D., Briegel, H. J., Cirac, J. I., Gardiner, C. W. & Zoller, P. Entanglement of atoms via cold controlled collisions. Phys. Rev. Lett. 82, 1975–1978 (1999).
Jaksch, D. et al. Fast quantum gates for neutral atoms. Phys. Rev. Lett. 85, 2208–2211 (2000).
DeMille, D. Quantum computation with trapped polar molecules. Preprint quant-ph/0109083 at http://xxx.lanl.gov (2001).
Jaksch, D., Bruder, C., Cirac, J. I., Gardiner, C. W. & Zoller, P. Cold bosonic atoms in optical lattices. Phys. Rev. Lett. 81, 3108–3111 (1998).
Spekkens, R. W. & Sipe, J. E. Spatial fragmentation of a Bose-Einstein condensate in a double-well potential. Phys. Rev. A 59, 3868–3877 (1999).
Orzel, C., Tuchman, A. K., Fenselau, M. L., Yasuda, M. & Kasevich, M. A. Squeezed states in a Bose-Einstein condensate. Science 291, 2386–2389 (2001).
Greiner, M., Mandel, O., Esslinger, T., Hänsch, T. W. & Bloch, I. Quantum phase transition from a superfluid to a Mott insulator in a gas of ultracold atoms. Nature 415, 39–44 (2002).
Cirac, I. & Zoller, P. A scalable quantum computer with ions in an array of microtraps. Nature 404, 579–581 (2000).
Monroe, C., Meekhof, D. M., King, B. E. & Wineland, D. J. A Schrödinger cat superposition state of an atom. Science 272, 1131–1136 (1996).
Bennett, C. H. et al. Purification of noisy entanglement and faithful teleportation via noisy channels. Phys. Rev. Lett. 76, 722–725 (1996).
Briegel, H.-J., Dür, W., Cirac, J. I. & Zoller, P. Quantum repeaters: the role of imperfect local operations in quantum communication. Phys. Rev. Lett. 81, 5932–5935 (1998).
Cirac, I., Zoller, P., Kimble, H. & Mabuchi, H. Quantum state transfer and entanglement distribution among distant nodes in a quantum network. Phys. Rev. Lett. 78, 3221–3224 (1997).
Law, C. & Kimble, H. Deterministic generation of a bit-stream of single-photon pulses. J. Mod. Opt. 44, 2067–2074 (1997).
van Enk, S., Cirac, I. & Zoller, P. Ideal quantum communication over noisy channels, a quantum optical implementation. Phys. Rev. Lett. 78, 4293–4296 (1997).
Ye, J., Vernooy, D. W. & Kimble, H. J. Trapping of single atoms in cavity QED. Phys. Rev. Lett. 83, 4987–4990 (1999).
Hood, C. J., Lynn, T. W., Doherty, A. C., Parkins, A. S. & Kimble, H. J. The atom-cavity microscope: single atoms bound in orbit by single photons. Science 287, 1447–1453 (2000).
Pinske, P., Fischer, T., Maunz, P. & Rempe, G. Trapping an atom with single photons. Nature 404, 365–368 (2000).
Doherty, A., Lynn, T. W., Hood, C. J. & Kimble, H. J. Trapping of single atoms with single photons in cavity QED. Phys. Rev. A 63, 013401-1–013401-24 (2001).
Guthöhrlein, G. R., Keller, M., Hayasaka, K., Lange, W. & Walther, H. A single ion as a nanoscopic probe of an optical field. Nature 414, 49–51 (2001).
Liu, C., Dutton, Z., Behroozi, C. H. & Hau, L. V. Observation of coherent optical information storage in an atomic medium using halted light pulses. Nature 409, 490–493 (2001).
Phillips, D. F., Fleischhauer, A., Mair, A., Walsworth, R. L. & Lukin, M. D. Storage of light in atomic vapor. Phys. Rev. Lett. 86, 783–786 (2001).
Budker, D., Kimball, D. F., Rochester, S. M. & Yashchuk, V. V. Nonlinear magneto-optics and reduced group velocity of light in atomic vapor with slow ground state relaxation. Phys. Rev. Lett. 83, 1767–1770 (1999).
Lukin, M. & Imamoglu, A. Controlling photons using electromagnetically induced transparency. Nature 413, 273–276 (2001).
Fleischhauer, M. & Lukin, M. Dark-state polaritons in electromagnetically induced transparency. Phys. Rev. Lett. 84, 5094–5097 (2000).
Mair, A., Hager, J., Phillips, D. F., Walsworth, R. L. & Lukin, M. D. Phase coherence and control of stored photonic information. Preprint quant-ph/0108046 at http://xxx.lanl.gov (2001).
Lukin, M. et al. Dipole blockade and quantum information processing in mesoscopic atomic ensembles. Phys. Rev. Lett 87, 037901-1–037901-4 (2001).
Hald, J., Sørensen, J. L., Schori, C. & Polzik, E. S. Spin squeezed atoms: a macroscopic entangled ensemble created by light. Phys. Rev. Lett. 83, 1319–1322 (1999).
Kuzmich, A., Mandel, L. & Bigelow, N. Generation of spin squeezing via continuous quantum nondemolition measurement. Phys. Rev. Lett. 85, 1594–1597 (2000).
Julsgaard, B., Kozhekin, A. & Polzik, E. Experimental long-lived entanglement of two macroscopic objects. Nature 413, 400–403 (2001).
Duan, L.-M., Lukin, M. D., Cirac, J. I. & Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 414, 413–418 (2001).
Wolf, F. A. Taking the Quantum Leap (Harper and Row, San Francisco, 1981).
Zurek, W. H. Decoherence and the transition from quantum to classical. Phys. Today 44, 34–44 (1991).
Braunstein, S. L., D'Ariano, G. M., Milburn, G. J. & Sacchi, M. F. Universal teleportation with a twist. Phys. Rev. Lett. 84, 3486–3489 (2000).
Acknowledgements
This work is supported by the US National Security Agency and Advanced Research and Development Activity under an Army Research Office contract, and by the National Science Foundation ITR programme.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Monroe, C. Quantum information processing with atoms and photons. Nature 416, 238–246 (2002). https://doi.org/10.1038/416238a
Issue Date:
DOI: https://doi.org/10.1038/416238a
This article is cited by
-
Dephasing effects on nonclassical correlations in two-qubit Heisenberg spin chain model with anisotropic spin–orbit interactions
Applied Physics B (2024)
-
Shortcuts to adiabaticity in superconducting circuits for fast multi-partite state generation
Communications Physics (2023)
-
Multi-stability in cavity QED with spin–orbit coupled Bose–Einstein condensate
Nonlinear Dynamics (2023)
-
Unfolding frequency and spatial multimode through parametric amplified cascade four-mode process
Applied Physics B (2023)
-
Dynamical Suppression of Decoherence and Protection of Quantum Coherence Between Superconducting Flux Qubits in 1/f Noise Environments by Bang-Bang Pulses
International Journal of Theoretical Physics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.