Relation between fractal dimension and spatial correlation length for extensive chaos

Abstract

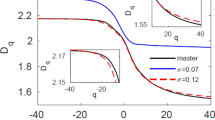
SUSTAINED nonequiibrium systems can be characterized by a fractal dimension D⩾0, which can be considered to be a measure of the number of independent degrees of freedom¹. The dimension D is usually estimated from time series² but the available algorithms are unreliable and difficult to apply when D is larger than about 5 (refs 3,4). Recent advances in experimental technique^5–8 and in parallel computing have now made possible the study of big systems with large fractal dimensions, raising new questions about what physical properties determine D and whether these physical properties can be used in place of time-series to estimate large fractal dimensions. Numerical simulations^9–11 suggest that sufficiently large homogeneous systems will generally be extensively chaotic¹², which means that D increases linearly with the system volume V. Here we test an hypothesis that follows from this observation: that the fractal dimension of extensive chaos is determined by the average spatial disorder as measured by the spatial correlation length ε associated with the equal-time two-point correlation function —a measure of the correlations between different regions of the system. We find that the hypothesis fails for a representative spatiotemporal chaotic system. Thus, if there is a length scale that characterizes homogeneous extensive chaos, it is not the characteristic length scale of spatial disorder.