Main

Dimensionality is one of the most basic and essential concepts in science, inherent to any theory aiming at explaining and predicting experimental observations. In building up a theoretical model, one makes some general and plausible assumptions about the nature and the behaviour of the system under study. The dimension of this system, that is, the number of relevant and independent degrees of freedom needed to describe it, represents one of these initial assumptions. In general, the failure of a theoretical model in predicting experimental data does not necessarily imply that the assumption on the dimensionality is incorrect, because there might exist a different model assuming the same dimension that is able to reproduce the observed data.

A natural question is whether this approach can be reversed and whether the dimension of an unknown system, classical or quantum, can be estimated experimentally. Clearly, the best one can hope for is to provide lower bounds on this unknown dimension. Indeed, every physical system has potentially an infinite number of degrees of freedom, and one can never exclude that they are all necessary to describe the system in more complex experimental arrangements. The goal, then, is to obtain a lower bound on the dimension of the unknown system from the observed measurement data without making any assumption about the detailed functioning of the devices used in the experiment. Besides its fundamental interest, estimating the dimension of an unknown quantum system is also relevant from the perspective of quantum information science, where the Hilbert space dimension is considered as a resource. For instance, using higher-dimensional Hilbert spaces simplifies quantum logic for quantum computation10, enables the optimal realization of information-theoretic protocols11,19,20 and allows for lower detection efficiencies in Bell experiments21,22. Moreover, the dimension of quantum systems plays a crucial role in security proofs of standard quantum key distribution schemes that become insecure if the dimension is higher than assumed12.

The concept of a dimension witness allows one to establish lower bounds on the dimension of an unknown system in a device-independent way, that is, only from the collected measurement statistics. It was first introduced for quantum systems in connection with Bell inequalities in ref. 1, and further developed in refs 2, 3, 22, 23, 24, 25, 26. Other techniques to estimate the dimension have been developed in scenarios involving random access codes4, or the time evolution of a quantum observable5.

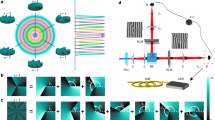
More recently, a general framework for the study of this question has been proposed in ref. 6. In this approach, dimension witnesses are defined in a prepare and measure scenario where an unknown system is subject to different preparations and measurements. One of the advantages of this approach is its simplicity from an experimental viewpoint when compared with previous proposals. The considered scenario consists of two devices (Fig. 1), the state preparator and the measurement device. These devices are seen as black boxes, as no assumptions are made on their functioning. The state preparator prepares a state on request. The box features N buttons that label the prepared state; when pressing button x, the box emits a state ρx, where x∈{1,…,N}. The prepared state is then sent to the measurement device. The measurement box performs a measurement y∈{1,…,M}on the state, delivering outcome b∈{1,…,K}. The experiment is thus described by the probability distribution P(b|x,y), giving the probability of obtaining outcome b when measurement y is performed on the prepared state ρx. The goal is to estimate the minimal dimension that the ensemble {ρx} must have to be able to describe the observed statistics. Moreover, for a fixed dimension, we also aim at distinguishing sets of probabilities P(b|x,y) that can be obtained from ensembles of quantum states, but not from ensembles of classical states. This allows one to guarantee the quantum nature of an ensemble of states under the assumption that the dimensionality is bounded. This quantum certification can be exploited for the design of quantum information protocols17,18.

Figure 1: Sketch of a device-independent test of the dimension of an ensemble of states.
figure 1

Our scenario features two black boxes. First, a state preparator that, on request, prepares the mediating particle in one out of N possible states. Second, a measurement device that performs one out of M possible measurements on the mediating particle.

Full size image

Formally, a probability distribution P(b|x,y) admits a quantum d-dimensional representation if it can be written in the form

for some state ρx and measurement operator Oby acting on . We then say that P(b|x,y) has a classical d-dimensional representation if any state of the ensemble is a classical state of dimension d, that is, a probability distribution over classical dits (the equivalent in quantum mechanics is that all states in the ensemble act on and commute pairwise).

A dimension witness for systems of dimension d is defined by a linear combination of the observed probabilities P(b|x,y), defined by a tensor of real coefficients Db,x,y, such that

for all probabilities with a d-dimensional representation, whereas the bound wd can be violated by a set of probabilities whose representation has a dimension strictly larger than d. Here we shall focus on a dimension witness of the form of equation (2) recently introduced in ref. 6, for a scenario consisting of N=4possible preparations and M=3 measurements with only two possible outcomes, labelled by b=±1:

where Ex y=P(b=+1|x,y)−P(b=−1|x,y). The witness I4 can distinguish ensembles of classical and quantum states of dimensions up to d=4. All of the relevant bounds are summarized in Table 1.

Table 1 Classical and quantum bounds for the dimension witness I4.
Full size table

To test this witness experimentally, we must generate classical and quantum states of dimension 2 (bits and qubits, respectively), classical and quantum states of dimension 3 (trits and qutrits), and classical states of dimension 4 (quarts). To do so we exploit the angular momentum of photons7,8, which contains a spin contribution associated with the polarization, and an orbital contribution associated with the spatial shape of the light intensity and its phase. Within the paraxial regime, both contributions can be measured and manipulated independently. The polarization of photons is conveniently represented by a two-dimensional Hilbert space, spanned by two orthogonal polarization states (for example, horizontal and vertical). The spatial degree of freedom of light lives in an infinite-dimensional Hilbert space27, spanned by paraxial Laguerre–Gaussian modes. Laguerre–Gaussian beams carry a well-defined orbital angular momentum (OAM) of mℏ (m is an integer) per photon that is associated with their spiral wavefronts28.

In our experiment, we use both the polarization and the OAM (m=±1) of photons to prepare quantum states of dimension up to 4, spanned by the orthogonal vectors |H,+1〉, |H,−1〉, |V,+1〉 and |V,−1〉, where |H,±1〉 (|V,±1〉) denotes a horizontally (vertically) polarized photon with OAM m=±1. We first generate, by means of spontaneous parametric down-conversion, pairs of photons (signal and idler) entangled in both polarization and OAM (Fig. 2). The entangled state is of the form , where and . By performing a projective measurement on the idler photon, we prepare the signal photon in a well-defined state of polarization and OAM. In particular, we project the idler photon on states of the form , which has the effect of preparing the signal photon in the state . Thus, the combination of the source of entanglement and the measurement of the idler photon represents the state preparator. The prepared state is encoded on the signal photon that is then measured. The signal photon represents the mediating particle between the state preparator and measurement device of Fig. 1.

Figure 2: Experimental set-up.
figure 2

a, The state preparator consists of a source of entangled photons (A), followed by a measurement (B) on one photon of the pair (idler) that prepares its twin photon (signal) in the desired state. The signal photon is then sent to the measurement device. Block (A) is the source of entangled photons. The second harmonic (Inspire Blue, Spectra Physics/Radiantis) at a wavelength of 405 nm of a Ti:sapphire laser in the picosecond regime (Mira, Coherent) is shaped by a spatial filter (SF) and focused into a 1.5-mm-thick crystal of beta-barium borate, where spontaneous parametric down-conversion takes place. The nonlinear crystal (XL) is cut for collinear type-II down-conversion so that the generated photons have orthogonal polarizations. Before splitting the signal and idler photon, a polarization-dependent temporal delay τ is introduced. The delay line (DL) consists of two quartz prisms whose mutual position determines the difference between the propagation times of photons with orthogonal polarizations. Block (B) performs a measurement on the idler photon to prepare the signal photon. It consists of a half-wave plate (HWP), polarizer (P), spatial-light modulator (SLM) and a Fourier-transform lens (FL). The half-wave plate and polarizer project the photon into the desired polarization state. The desired OAM state is selected by the SLM. SLM encodes computer-generated holograms that transform the m=+1 state or m=−1 state into the fundamental Laguerre–Gaussian state LG00 (ref. 7) that is coupled into a single-mode fibre (SMF). The measurement device uses an identical block (B) to measure the signal photon. M: mirrors; L: lenses; BS: beam splitter, F: interference filter; D: single-photon counting modules. b, Ensembles of quantum states |ϕx〉 (x=1…4) prepared in the experiment. c, Measurements performed at the measurement device for qubits and qutrits. In the case of quarts, the three measurements are constructed by combining (1) and (2).

Full size image

To implement a continuous transition from quantum to classical states, a polarization-dependent temporal delay τ between the signal and idler photons is introduced. If the temporal delay between the photons exceeds their correlation time, the coherence is lost; that is, the off-diagonal terms vanish for all states in the ensemble (see Supplementary Information).

For the sake of clarity, we list the assumptions made when processing the observed data: the statistical behaviour of P(b|x y), described by equation (1), is the same at every run of the experiment; the detectors used for the preparation and the measurement are uncorrelated; the observer can freely choose the preparation and measurement in each run; the observed statistics provide a fair sample of the total statistics that would have been observed with perfect detectors. All of these assumptions are standard in any estimation scenario. The value of the dimension witnesses is then calculated from the raw data, that is, from all of the observed coincidences between detection at the preparator and at the measuring device, including dark counts. In the experiment we first generate and measure the four qubit states |ϕx〉 given in Fig. 2. The first measurement (y=1) assigns dichotomic measurement results of b=+1 and b=−1 to horizontally and vertically polarized photons, respectively. The second measurement (y=2) assigns b=+1 and b=−1 to OAM values of m=+1 and m=−1, respectively. The third measurement (y=3) assigns b=+1 and b=−1 to photons polarized at +45° and −45°, respectively. The expected value of the dimension witness of equation (3) for this combination of states and measurements is (see Supplementary Information). From our experimental data we obtain I4=5.66±0.15. This clearly demonstrates the quantum nature of our two-dimensional system, because classical bits always satisfy I4≤5.

In the above, the delay between signal and idler photons was set to τ=0. Now we gradually increase this delay to convert a qubit into a classical bit. The measured value of the witness I4 then drops below 5, as expected (blue triangles in Fig. 3).

Figure 3: Dimension witness I4 for qubit (blue triangles), qutrit (red circles) and quart (green diamonds) states as a function of temporal delay τ.
figure 3

For delays τ>255 fs, coherence is lost and quantum superpositions turn into statistical mixtures, that is, classical states. The maximum observed violations for qubit, qutrit and quart states are 5.66±0.15, 7.57±0.13 and 8.57±0.06, respectively. These values are close to the corresponding theoretical bounds, given in Table 1, which are represented here by the horizontal lines. The error bars plot standard deviations on the value of the witness calculated from the measured data using error propagation rules.

Full size image

Next we generate ensembles of qutrits. The prepared states and the measurements are identical to the previous (qubit) experiment, except that the OAM of state |ϕ3〉 is now flipped. For τ=0, we obtain a measured value of the witness of I4=7.57±0.13, certifying the presence of a quantum system of dimension (at least) 3. This value is in good agreement with the theoretical prediction of for this set of states and measurements.

Now, increasing again delay τ between the photons, the value of the witness drops below 7. In a certain range of delays, the value of I4 remains above the qubit bound of 6, testifying that at least three dimensions are present (red circles of Fig. 3). In the limit of large delays, the values of the witness are still larger than the bound of I4=5 for bits, but below the bound for qubits. This is because the curve was measured with a set a measurements optimized for the qutrit/trit discrimination. This set of measurements is not optimum for the trit/qubit discrimination.

Finally, we prepare classical four-dimensional systems, that is, quarts. Now the first measurement (y=1) assigns the outcome b=−1 to vertically polarized photons with OAM m=−1, and the outcome b=+1 to all of the other orthogonal states. The second measurement (y=2) assigns b=+1 and b=−1 to horizontally and vertically polarized photons, respectively. The third measurement (y=3) assigns b=+1 and b=−1 to OAM of m=+1 and m=−1, respectively. In this case, the expected value of the witness is I4=9, which corresponds to the algebraic maximum. Experimentally, we measure I4=8.57±0.06, which violates the qutrit bound of I4=7.97 by more than 10 standard deviations. In this case, the values of the witness are independent of the temporal delay τ. This is because the state is here classical (a statistical mixture of orthogonal quantum states) and no superposition is present (green diamonds in Fig. 3).

We have demonstrated how the concept of dimensionality, which is fundamental in science, can be experimentally tested. Using dimension witnesses, we have bounded the dimension of classical and quantum systems only from measurement statistics, without any assumption on the internal working of the devices used in the experiment. Dimension witnesses represent an example of a device-independent estimation technique, in which relevant information about an unknown system is obtained solely from the measurement data. Device-independent techniques13,14,15,16 provide an alternative approach to existing quantum estimation techniques, such as quantum tomography or entanglement witnesses, which crucially rely on assumptions that may be questionable in complex set-ups, for example, its Hilbert space dimension. Our work demonstrates how the device-independent approach can be employed to experimentally estimate the dimension of an unknown system.