Abstract
Three-dimensional (3D) topologicalWeyl semimetals (TWSs) represent a state of quantum matter with unusual electronic structures that resemble both a ‘3D graphene’ and a topological insulator. Their electronic structure displays pairs of Weyl points (through which the electronic bands disperse linearly along all three momentum directions) connected by topological surface states, forming a unique arc-like Fermi surface (FS). Each Weyl point is chiral and contains half the degrees of freedom of a Dirac point, and can be viewed as a magnetic monopole in momentum space. By performing angle-resolved photoemission spectroscopy on the non-centrosymmetric compound TaAs, here we report its complete band structure, including the unique Fermi-arc FS and linear bulk band dispersion across the Weyl points, in agreement with the theoretical calculations1,2. This discovery not only confirms TaAs as a 3DTWS, but also provides an ideal platform for realizing exotic physical phenomena (for example, negative magnetoresistance, chiral magnetic effects and the quantum anomalous Hall effect) which may also lead to novel future applications.
Similar content being viewed by others
Main
The discovery of quantum materials with non-trivial topological electronic structures, such as topological insulators, topological crystalline insulators and Dirac semimetals3,4,5,6,7,8,9, has recently ignited worldwide interest owing to their rich scientific implications and broad application potentials3,4,5,6,7,8,9. Although being the subject of condensed matter physics, the research on topological quantum matter has benefited from the connection to other fields of physics, such as high-energy physics, by the introduction of Dirac and Majorana fermions into the electronic spectra of crystals. Recently, another intriguing particle—the Weyl fermion—which was also originally introduced in high-energy physics (for example, as a description of neutrinos), is proposed to have its counterpart in solid state physics10, leading to a new type of topological quantum matter, the topological Weyl semimetals (TWSs; refs 1, 2, 10, 11, 12).
A TWS exhibits unique band structures that resemble both a ‘3D graphene’ and a topological insulator. On one hand, the bulk conduction and valence bands of a TWS touch linearly at pairs of discrete points—the Weyl points, through which the bands disperse linearly along all three momentum directions (thus it is a 3D analogue of graphene); as Weyl points of opposite chirality can be either a ‘source’ or ‘sink’ of Berry curvature1,2,10 (Fig. 1a), they can also be viewed as magnetic monopoles in the momentum space. On the other hand, in a TWS, there exist unique surface Fermi arcs1,2,10,11,12 (Fig. 1a), or unclosed Fermi surfaces (FSs) originating from the topological surface states (similar to those in topological insulators) that start and end at the Weyl points of opposite chirality (Fig. 1a). The unique bulk Weyl fermions and the surface Fermi arcs can give rise to many unusual physical phenomena, such as negative magnetoresistance, the chiral magnetic effect, the quantum anomalous Hall effect, novel quantum oscillations (in magnetotransport) and quantum interference (in tunnelling spectroscopy)13,14,15,16,17.
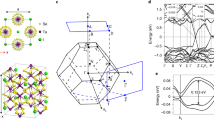
a, Illustration of the splitting of a Dirac point (DP). A DP can be split into a pair of Weyl points with opposite chirality (marked as WP+ and WP−) which behave as a ‘source’ or ‘sink’ of Berry curvature by breaking time-reversal or inversion symmetry (see text for discussions). The two Weyl points are connected by the Fermi-arc-type of FS formed by the topological surface states. b, Crystal structure of TaAs, showing the ⋯ A–B–C–D ⋯ stacking of TaAs layers. c, Schematic of the bulk and (001) surface Brillouin zones (BZs) of TaAs. Twelve pairs of Weyl points are predicted in each BZ, with four pairs at each of the kz = 0 and ±1.16π/c planes, respectively. d, FSs from ab initio calculations are plotted on the (001) surface BZ with the (projected) Weyl points (in red and blue) overlaid, showing the characteristic Fermi-arc FS geometry. The colour bar shows the surface contribution of the FS (white/0% to red/100%), same in Figs 2–4 below. e, (i) Image of a TaAs single crystal with a flat cleavage plane used for ARPES measurements. (ii–iv) X-ray diffraction patterns of the TaAs crystal from different crystalline directions. f, Core-level photoemission spectrum clearly showing the characteristic As 3d, Ta 5p and 4f peaks. g, Broad FS map confirming the (001) cleavage plane and the lattice constant in b. The uneven intensity of the FS at different BZs results from the matrix element effect. The colour bar shows the ARPES spectra intensity, from white (lowest) to blue (highest), same in Figs 2–4 below.
In principle, TWSs can be realized by breaking either time-reversal symmetry or inversion symmetry12,18 of recently discovered topological Dirac semimetals9,19,20,21. In this way, the bulk Dirac point in a topological Dirac semimetal can be split into two Weyl points (Fig. 1a), thus realizing the TWS state. However, this method does not generate intrinsic TWSs and the need for a high external magnetic field or mechanical strain requires complicated instrumentation and experimental set-up (thus limiting the use and application of these materials). Under this circumstance, the pursuit of intrinsic materials with spontaneously broken symmetry has become the focus of current research. So far, several candidates with naturally broken time-reversal symmetry have been proposed (for example, Y2Ir2O7 (ref. 10) and HgCr2Se4 (ref. 11)), however, none of them have been experimentally confirmed, leaving the existence of the TWS elusive.
Recently, another type of TWS candidate with naturally broken inversion symmetry was proposed in several compound families, including finely tuned solid solutions LaBi1−xSbxTe3, LuBi1−xSbxTe3 (ref. 22) and transition metal monoarsenides/phosphides (including TaAs, TaP, NbAs and NbP; refs 1, 2). In this work, by using angle-resolved photoemission spectroscopy (ARPES), we systematically studied the electronic structure of single-crystal TaAs and observed the unique surface Fermi arcs on its FS as well as the linear bulk band dispersions through the Weyl points. The excellent agreement between our experimental band structures and ab initio calculations (including previous theoretical predictions1,2) clearly establishes that TaAs is a TWS.
The crystal structure of TaAs is shown in Fig. 1b. There are four TaAs layers in a unit cell along the c-direction, forming a repeating ⋯ –A–B–C–D– ⋯ stacking structure23 without inversion symmetry (Fig. 1b). As the distances in the c-direction between the intra- and inter-layer Ta and As planes are 0.083c (0.966 Å) and 0.167c (1.944 Å), respectively, the crystal cleaves naturally between adjacent TaAs layers along the (001) plane (Fig. 1b, e(i)), which is ideal for the ARPES measurements. In recent theoretical investigations1,2, TaAs was proposed as a TWS candidate with twelve pairs of Weyl points in each Brillouin zone (BZ; Fig. 1c), with each pair of Weyl points connected by topologically non-trivial surface states, forming the unique surface Fermi arcs. The characteristic FS of TaAs with the surface Fermi arcs on the (001) surface from our ab initio calculations (details of the calculations can be found in Methods) is shown in Fig. 1d, in nice agreement with the previous theoretical works1,2.
High-quality TaAs crystals were synthesized (details of growth can be found in Methods) for our ARPES measurements (Fig. 1e(i)), showing flat and shiny cleaved surfaces. The X-ray diffraction along different crystalline orientations (Fig. 1e(ii–iv)) confirmed the crystal structure. The core-level photoemission spectrum (Fig. 1f) shows sharp characteristic Ta 5p, 4f and As 3d core levels and the broad FS mapping (Fig. 1g) illustrates the overall FS topology agreeing with the ab initio calculations in Fig. 1d (fine measurements with more details will be discussed below).
Owing to the intrinsic surface sensitivity, ARPES is an ideal tool to study the unusual surface states and search for the unique surface Fermi arcs in TaAs. In Fig. 2, we illustrate the overall FS geometry and the band structure evolution with different binding energies around both  and
and  points of the surface BZ.
points of the surface BZ.
a, 3D intensity plot of the photoemission spectra around the  point, showing the band dispersions and the resulting FSs. The spoon-like α-FSs are marked. b, Comparison showing excellent agreement between experiments (left) and ab initio calculations (right) of three constant energy contours at different binding energies. The spoon/bowtie-like α/β-FSs (see text) are marked. For better comparison with calculations, the experimental plot has been symmetrized with respect to the ky = 0 plane according to the crystal symmetry (as also has been done in e below). c, Comparison of measured (upper) and calculated (lower) dispersions along the high-symmetry direction
point, showing the band dispersions and the resulting FSs. The spoon-like α-FSs are marked. b, Comparison showing excellent agreement between experiments (left) and ab initio calculations (right) of three constant energy contours at different binding energies. The spoon/bowtie-like α/β-FSs (see text) are marked. For better comparison with calculations, the experimental plot has been symmetrized with respect to the ky = 0 plane according to the crystal symmetry (as also has been done in e below). c, Comparison of measured (upper) and calculated (lower) dispersions along the high-symmetry direction  . d–f, Same as a–c, but around the
. d–f, Same as a–c, but around the  point. g,h, Photon-energy-dependent ARPES measurement plot of photoemission intensities at EF along the high-symmetry directions
point. g,h, Photon-energy-dependent ARPES measurement plot of photoemission intensities at EF along the high-symmetry directions  (g) and
(g) and  (h) as function of photon energy (48–68 eV), showing the kz dispersion of different bands. The α bands in c,f are labelled.
(h) as function of photon energy (48–68 eV), showing the kz dispersion of different bands. The α bands in c,f are labelled.
The 3D band structures around both  and
and  regions are presented in Fig. 2a and d respectively, which illustrate the FS geometry with related band dispersions. In Fig. 2b, e, three constant energy contours at different binding energies are selected to show the band evolution around the
regions are presented in Fig. 2a and d respectively, which illustrate the FS geometry with related band dispersions. In Fig. 2b, e, three constant energy contours at different binding energies are selected to show the band evolution around the  and
and  points—both vary from the cross-shaped FSs to more complicated shapes at higher binding energy. Each set of cross-shaped FSs (Fig. 2b(i), e(i)) is comprised of two orthogonal subsets of FSs, one forms spoon-like pockets (marked as α-FSs) and the other forms bowtie-shaped pockets (marked as β-FSs)—all of these FSs agree well with our ab initio calculations (presented side by side in Fig. 2b, e).
points—both vary from the cross-shaped FSs to more complicated shapes at higher binding energy. Each set of cross-shaped FSs (Fig. 2b(i), e(i)) is comprised of two orthogonal subsets of FSs, one forms spoon-like pockets (marked as α-FSs) and the other forms bowtie-shaped pockets (marked as β-FSs)—all of these FSs agree well with our ab initio calculations (presented side by side in Fig. 2b, e).
Besides the FS topology, we also studied the band dispersions across the BZ (Fig. 2c, f). The comparison between the measurements and calculations again shows excellent agreement (see Supplementary Fig. 1 for more comparisons). The surface nature of the bands that form the spoon-like α-FSs (Fig. 2a, b(i), d, e(i)) can be verified by photon-energy-dependent ARPES measurements24 (Fig. 2g, h), where the ARPES spectra clearly show no kz-dispersion (that is, vertical dispersions; see Supplementary Information), in contrast to the bulk band dispersion which we will discuss later.
After establishing the overall correspondence between the experimental and theoretical band structures, we zoom into the spoon-like α-FSs by performing fine ARPES mapping with high resolution to study the detailed FS geometry and search for the unusual surface Fermi arcs—the unique signature of a TWS.
In Fig. 3a, our ab initio calculations show a clear surface Fermi arc (green curve, marked as FS-1) terminating at the Weyl points (see Fig. 3a inset for clarity), whereas the other two FS segments (FS-2, FS-3) extend across the Weyl points. This unusual FS topology was indeed experimentally observed in Fig. 3b, which matches Fig. 3a excellently. The change in the FS segments across the Weyl points in the experiment can also be verified through the band dispersions (Fig. 3c). Evidently, measurements above the Weyl points (Fig. 3c(i–iii)) show three bands dispersing across EF, whereas there are only two bands crossing EF below the Weyl points (Fig. 3c(iv–vi)), caused by the termination of FS-1 at the Weyl points. Further discussions on the nature (including the spin polarization) and evolution of each FS segment, as well as quantitative momentum distribution curve (MDC) analysis can be found in the Supplementary Information.
a, Calculated FS geometry with a fine k-space grid around the  point of the BZ showing the Fermi-arc FS (green curve, see text and refs 1, 2 for discussion). Different FS segments are colour coded (with contributions indicated by the colour bar) and labelled as FS 1-3. The inset shows the detailed evolution of different FS segments around the Weyl point. b, FS measured using ARPES at high resolution showing excellent agreement with a. The dashed line connects the two Weyl points for reference. The six arrows above and below the dashed line indicate the measurement positions in c. For better comparison with the calculation in a, the plot has been symmetrized with respect to kx = 0 according to the crystal symmetry (this applies also to c and d). c, Three band dispersions measured above and below the dashed line in b (at the locations indicated by the red and green arrows in b, respectively). Band dispersions labelled 1–3 correspond to the equivalently labelled FS segments in b. The plot has been symmetrized with respect to kx = 0 according to the crystal symmetry. d, (i–iii) Dispersions from ARPES measurements along different high-symmetry directions showing excellent agreement with the overlaid ab initio calculations (red curves). The Fermi crossing locations 1–7 are marked by green arrows in (ii) and (iii). The corresponding positions are also marked in the surface BZ in (iv) together with the Weyl points (blue and red points).
point of the BZ showing the Fermi-arc FS (green curve, see text and refs 1, 2 for discussion). Different FS segments are colour coded (with contributions indicated by the colour bar) and labelled as FS 1-3. The inset shows the detailed evolution of different FS segments around the Weyl point. b, FS measured using ARPES at high resolution showing excellent agreement with a. The dashed line connects the two Weyl points for reference. The six arrows above and below the dashed line indicate the measurement positions in c. For better comparison with the calculation in a, the plot has been symmetrized with respect to kx = 0 according to the crystal symmetry (this applies also to c and d). c, Three band dispersions measured above and below the dashed line in b (at the locations indicated by the red and green arrows in b, respectively). Band dispersions labelled 1–3 correspond to the equivalently labelled FS segments in b. The plot has been symmetrized with respect to kx = 0 according to the crystal symmetry. d, (i–iii) Dispersions from ARPES measurements along different high-symmetry directions showing excellent agreement with the overlaid ab initio calculations (red curves). The Fermi crossing locations 1–7 are marked by green arrows in (ii) and (iii). The corresponding positions are also marked in the surface BZ in (iv) together with the Weyl points (blue and red points).
Interestingly, as a Fermi arc is an unclosed FS, we can also verify the existence of Fermi arcs by counting the total number of Fermi crossings along a closed loop in the BZ that encloses an odd number of Weyl points—and get an odd total number of Fermi crossings (see Supplementary Information for further details on the principles of Fermi crossing counting). We thus choose the  loop in a BZ (see Fig. 3d(iv)) which encloses three Weyl points, including two degenerate points (red colour, at different kz, but projected to the surface BZ at the same location, see Fig. 1c, d for details) and a singular point (blue colour). In Fig. 3d, the counting of the Fermi crossings along the sections
loop in a BZ (see Fig. 3d(iv)) which encloses three Weyl points, including two degenerate points (red colour, at different kz, but projected to the surface BZ at the same location, see Fig. 1c, d for details) and a singular point (blue colour). In Fig. 3d, the counting of the Fermi crossings along the sections  (panel (ii)),
(panel (ii)),  (panel (iii)) and
(panel (iii)) and  (panel (i)) yields five, two and zero crossings, respectively. Thus there are a total of seven (an odd number) Fermi crossings along the loop
(panel (i)) yields five, two and zero crossings, respectively. Thus there are a total of seven (an odd number) Fermi crossings along the loop  , which confirms the existence of the Fermi arcs on the FS of TaAs (see Supplementary Information for Fermi crossing counting along the
, which confirms the existence of the Fermi arcs on the FS of TaAs (see Supplementary Information for Fermi crossing counting along the  loop).
loop).
In addition to the unique surface Fermi arcs, we also carried out ARPES measurements (Fig. 4) with high photon energies to investigate the bulk band structure of TaAs. In Fig. 4b, bulk bands with strong kz dispersion can be clearly seen in the ky–kz spectra intensity map (in contrast to the surface α-bands in Fig. 2g, h without kz dispersion; see Supplementary Information for futher details), agreeing well with our calculation (overlaid on Fig. 4b, note that the Weyl points are not observed here as they are off the kx = 0 plane, see Fig. 1c, d). Also, the measured dispersions along the high-symmetry directions show good agreement with calculations (Fig. 4c, d).
a, Schematic of the measurement ky–kz plane (vertical grey plane) of the intensity plot in b. Weyl points are also shown. b, Photoemission intensity plot of the ky–kz plane (kx = 0, the grey plane in a). The integration window is from EF − 100 meV to EF (see Supplementary Information for more information). Overlaid yellow curves are calculated bulk bands’ constant energy contours at the centre energy of the intensity map (EF − 50 meV), showing excellent agreement with the experiment. Green and magenta curves indicate the kz momentum locations probed by 204 eV and 189 eV photons, respectively. The two dashed lines marked as ‘cut1’ and ‘cut2’ indicate the momentum direction of the two band dispersions shown in c and d. c,d, Bulk band dispersions along two high-symmetry directions, indicated as cut1 and cut2 in b, respectively. The calculated band dispersions (red curves) are overlaid. e, (i) Schematic illustration of the kz measurement plane (large grey plane) for 189 eV photons that cut through the Weyl points at kz = −1.16π/c (in the reduced BZ). (ii) FS map of the kx–ky plane using 189 eV photons with an integration window from EF − 20 meV to EF + 20 meV, with the calculated FS overlaid (orange pockets). Black dashed line indicates the measurement direction of the band dispersion in f, and the blue lines indicate the kx–ky BZ at kz = −1.16π/c (in the reduced BZ). For better comparison with calculations, the experiment plot has been symmetrized with respect to the kx = 0 and ky = 0 planes according to the crystal symmetry (same in f–h). The uneven spectra intensities between the kx = 0 and ky = 0 directions are due to the matrix element effect. f, Broadband dispersion (i) and a zoomed-in plot (ii) across the Weyl points (along the direction indicated by the dashed line in e (ii)); the inset of (ii) shows the detailed band dispersion around the Weyl points without the calculations overlaid for clarity. g,h, Same as e,f for a photon energy of 204 eV (through the Weyl points at kz = 0 (in the reduced BZ)).
The excellent agreements between our experiments and calculations allow us to identify the Weyl points predicted as lying at the kz = ±1.16π/c and kz = 0 planes (Fig. 1c), which can be accessed using 189 eV (kz = −1.16π/c in the reduced BZ) and 204 eV (kz = 0 in the reduced BZ) photons, respectively (see Fig. 4b). At each photon energy, we first carried out kx–ky FS mapping (Fig. 4e, g) to locate the in-plane momentum positions of the Weyl points, then measured the band dispersions across them (Fig. 4f, h). Indeed, the measured bulk band dispersions in both cases show clear linear dispersions that again match well with our calculations (Fig. 4f, h), confirming the existence of Weyl points in the bulk band structure of TaAs (see Supplementary Information for further details).
The observation of the unique surface Fermi arcs and the bulk Weyl points with linear dispersions, together with the overall agreement of the measurements with the theoretical calculations, establish TaAs as the first TWS experimentally observed. This discovery extends the possibilities for the exploration of other exotic phenomena associated with TWSs and potential applications that would benefit from the ultrahigh mobility and unusually large (and non-saturating) magnetoresistance in recently discovered 3D semimetals25,26.
We note that while we were finalizing this manuscript, two other groups also independently studied the compound TaAs (refs 27, 28), and the Weyl points were also observed in a photonic crystal29.
Methods
Sample synthesis.
Precursor polycrystalline TaAs samples were prepared by mixing high-purity (>99.99%) Ta and As elements. The mixture was sealed into a quartz tube under high vacuum, which was again sealed into another evacuated tube for extra protection. First, the vessel was heated to 600 °C at the rate of 50 °C h−1, then, after 10 h of soaking, it was slowly heated to 1,050 °C at the rate of 30 °C h−1 and kept at this temperature for 24 h. Finally the vessel was cooled down to room temperature.
From the polycrystalline precursor, the single crystals were grown using the chemical vapour transport method in a two-zone furnace. The polycrystalline TaAs powder and 0.46 mg cm−3 of iodine were loaded into a 24-mm-diameter quartz tube and sealed under vacuum. The charged part of the tube was kept at 1,150 °C and the other end at 1,000 °C for three weeks. The resulting crystals can be as large as 0.5–1 mm in size.
Angle-resolved photoemission spectroscopy.
ARPES measurements were performed at beamline 10.0.1 of the Advanced Light Source (ALS) at the Lawrence Berkeley National Laboratory and BL I05 of the Diamond Light Source (DLS). The measurement pressure was kept below 3 × 10−11/9 × 10−11 torr in the two facilities, and data were recorded by Scienta R4000 analysers at a 10 K sample temperature. The total convolved energy and angle resolutions were 16 meV and 0.2°, respectively. A fresh surface of TaAs for the ARPES measurement was obtained by cleaving the TaAs sample in situ along its natural (001) cleavage plane.
Local density approximation (LDA) calculations.
Electronic structures were calculated using the density-functional theory (DFT) method which is implemented in the Vienna ab initio simulation package (VASP; ref. 30). The core electrons were represented by the projected augmented wave method31. The exchange–correlation was considered in the generalized gradient approximation (GGA; ref. 32) and spin–orbital coupling (SOC) was included self-consistently. The energy cut-off was set to be 300 eV for the plane-wave basis. Experimental lattice parameters were used in the construction of a slab model with a thickness of seven unit cells to simulate a surface, in which the top and bottom surface are terminated by As and Ta, respectively. The positions of the outermost four atomic layers were fully optimized in determining the surface atomic relaxation. The surface band structures and the FSs were projected to the first unit cell of the As-terminated side, which fits the experimental band structure well. We adopted 12 × 12 and 400 × 400 k-point grids in the charge self-consistent and FS calculations, respectively.
Change history
03 September 2015
In the version of this Letter originally published a description of arc-like Fermi surfaces in the abstract contained a typographical error. This error has been corrected in the online versions.
References
Weng, H., Fang, C., Fang, Z., Bernevig, A. & Dai, X. Weyl semimetal phase in non-centrosymmetric transition metal monophosphides. Phys. Rev. X 5, 011029 (2015).
Huang, S.-M. et al. An inversion breaking Weyl semimetal state in the TaAs material class. Nature Commun. 6, 7373 (2015).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Chen, Y. L. et al. Experimental realization of a three-dimensional topological insulator, Bi2Te3 . Science 325, 178–181 (2009).
Fu, L. Topological crystalline insulators. Phys. Rev. Lett. 106, 106802 (2011).
Dziawa, P. et al. Topological crystalline insulator states in Pb1−xSnxSe. Nature Mater. 11, 1023–1027 (2012).
Wang, Z. et al. Dirac semimetal and topological phase transitions in A3Bi (A = Na, K, Rb). Phys. Rev. B 85, 195320 (2012).
Liu, Z. K. et al. Discovery of a three-dimensional topological Dirac semimetal, Na3Bi. Science 343, 864–867 (2014).
Wan, X., Turner, A. M., Vishwanath, A. & Savrasov, S. Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101 (2011).
Xu, G., Weng, H., Wang, Z., Dai, X. & Fang, Z. Chern semimetal and the quantized anomalous Hall effect in HgCr2Se4 . Phys. Rev. Lett. 107, 186806 (2011).
Burkov, A. A. & Balents, L. Weyl semimetal in a topological insulator multilayer. Phys. Rev. Lett. 107, 127205 (2011).
Zyuzin, A. A. & Burkov, A. A. Topological response in Weyl semimetals and the chiral anomaly. Phys. Rev. B 86, 115133 (2012).
Liu, C.-X., Ye, P. & Qi, X.-L. Chiral gauge field and axial anomaly in a Weyl semimetal. Phys. Rev. B 87, 235306 (2013).
Landsteiner, K. Anomalous transport of Weyl fermions in Weyl semimetals. Phys. Rev. B 89, 075124 (2014).
Potter, A. C., Kimchi, I. & Vishwanath, A. Quantum oscillations from surface Fermi arcs in Weyl and Dirac semimetals. Nature Commun. 5, 5161 (2014).
Hosur, P. Friedel oscillations due to Fermi arcs in Weyl semimetals. Phys. Rev. B 86, 195102 (2012).
Halász, G. B. & Balents, L. Time-reversal invariant realization of the Weyl semimetal phase. Phys. Rev. B 85, 035103 (2012).
Liu, Z. K. et al. A stable three-dimensional topological Dirac semimetal Cd3As2 . Nature Mater. 13, 677–681 (2014).
Neupane, M. et al. Observation of a three-dimensional topological Dirac semimetal phase in high-mobility Cd3As2 . Nature Commun. 5, 3786 (2014).
Borisenko, S. et al. Experimental realization of a three-dimensional Dirac semimetal. Phys. Rev. Lett. 113, 027603 (2014).
Liu, J. & Vanderbilt, D. Weyl semimetals from noncentrosymmetric topological insulators. Phys. Rev. B 90, 155316 (2014).
Furuseth, S., Selte, K. & Kjekshus, A. On the arsenides and antimonides of tantalum. Acta Chem. Scand. 19, 95–106 (1965).
Chen, Y. Studies on the electronic structures of three-dimensional topological insulators by angle resolved photoemission spectroscopy. Front. Phys. 7, 175–192 (2012).
Liang, T. et al. Ultrahigh mobility and giant magnetoresistance in the Dirac semimetal Cd3As2 . Nature Mater. 14, 280–284 (2015).
Shekhar, C. et al. Extremely large magnetoresistance and ultrahigh mobility in the topological Weyl semimetal candidate NbP. Nature Phys. 11, 645–649 (2015).
Xu, S.-Y. et al. Discovery of a Weyl Fermion semimetal and topological Fermi arcs. Sciencehttp://dx.doi.org/10.1126/science.aaa9297 (2015).
Lv, B. Q. et al. Experimental discovery of Weyl semimetal TaAs. Phys. Rev. X 5, 031013 (2015).
Lu, L. et al. Experimental observation of Weyl points. Sciencehttp://dx.doi.org/10.1126/science.aaa9273 (2015).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Acknowledgements
Y.L.C. acknowledges the support from the EPSRC (UK) grant EP/K04074X/1 and a DARPA (US) MESO project (no. N66001-11-1-4105). The Advanced Light Source is operated by the Department of Energy, Office of Basic Energy Science (contract DE-AC02-05CH11231).
Author information
Authors and Affiliations
Contributions
Y.L.C. conceived the experiments. L.X.Y. and Z.K.L. carried out ARPES measurements with the assistance of H.P., H.F.Y., T.Z., B.Z., Y.Z. and S.-K.M. D.P., Y.F.G. and M.R. synthesized and characterized bulk single crystals. B.Y. and Y.S. performed ab initio calculations. All authors contributed to the scientific planning and discussions.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary information
Supplementary information (PDF 1709 kb)
Rights and permissions
About this article
Cite this article
Yang, L., Liu, Z., Sun, Y. et al. Weyl semimetal phase in the non-centrosymmetric compound TaAs. Nature Phys 11, 728–732 (2015). https://doi.org/10.1038/nphys3425
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nphys3425
This article is cited by
-
The discovery of three-dimensional Van Hove singularity
Nature Communications (2024)
-
Realization of practical eightfold fermions and fourfold van Hove singularity in TaCo2Te2
npj Quantum Materials (2023)
-
High-pressure induced Weyl semimetal phase in 2D Tellurium
Communications Physics (2023)
-
Topological classification for intersection singularities of exceptional surfaces in pseudo-Hermitian systems
Communications Physics (2023)
-
Emergence of Weyl fermions by ferrimagnetism in a noncentrosymmetric magnetic Weyl semimetal
Nature Communications (2023)