Abstract
It remains unclear whether causal, rather than merely correlational, relationships in molecular networks can be inferred in complex biological settings. Here we describe the HPN-DREAM network inference challenge, which focused on learning causal influences in signaling networks. We used phosphoprotein data from cancer cell lines as well as in silico data from a nonlinear dynamical model. Using the phosphoprotein data, we scored more than 2,000 networks submitted by challenge participants. The networks spanned 32 biological contexts and were scored in terms of causal validity with respect to unseen interventional data. A number of approaches were effective, and incorporating known biology was generally advantageous. Additional sub-challenges considered time-course prediction and visualization. Our results suggest that learning causal relationships may be feasible in complex settings such as disease states. Furthermore, our scoring approach provides a practical way to empirically assess inferred molecular networks in a causal sense.
Similar content being viewed by others
Main
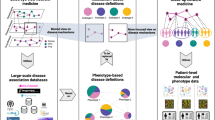
Molecular networks are central to biological function, and the data-driven learning of regulatory connections in molecular networks has long been a key topic in computational biology1,2,3,4,5,6. An emerging notion is that networks describing a certain biological process (e.g., signal transduction or gene regulation) may depend on biological contexts such as cell type, tissue type and disease state7,8. This has motivated efforts to elucidate networks that are specific to such contexts9,10,11,12,13,14. In disease settings, networks specific to disease contexts could improve understanding of the underlying biology and potentially be exploited to inform rational therapeutic interventions.
In this study we considered inference of causal molecular networks, focusing specifically on signaling downstream of receptor tyrosine kinases. We define edges in causal molecular networks ('causal edges') as directed links between nodes in which inhibition of the parent node can lead to a change in the abundance of the child node (Fig. 1a), either by direct interaction or via unmeasured intermediate nodes (Fig. 1b). Such edges may be specific to biological context (Fig. 1c). The notion of a causal link is fundamentally distinct from a correlational link (Fig. 1d). Causal network inference is profoundly challenging15,16, and many methods for inferring regulatory networks connect correlated, or mutually dependent, nodes that might not have any causal relationship. Some approaches (e.g., directed acyclic graphs17,18,19) can in principle be used to infer causal relationships, but their success can be guaranteed only under strong assumptions15,20 that are almost certainly violated in biological settings. This is due to many limitations—some possibly fundamental—in our ability to observe and perturb biological systems.
(a) A directed edge denotes that inhibition of the parent node A can change the abundance of the child node B. (b) Causal edges, as used here, may represent direct effects or indirect effects that occur via unmeasured intermediate nodes. If node A causally influences node B via measured node C, the causal network should contain edges from A to C and from C to B, but not from A to B (top). However, if node C is not measured (and is not part of the network), the causal network should contain an edge from A to B (bottom). Note that in both cases inhibition of node A will lead to a change in node B. (c) Causal edges may depend on biological context; for example, a causal edge from A to B appears in context 1, but not in context 2 (lines in graphs are as defined in a). (d) Correlation and causation. Nodes A and B are correlated owing to regulation by the same node (C), but in this example no sequence of mechanistic events links A to B, and thus inhibition of A does not change the abundance of B (lines in bottom right graph are as defined in a). Therefore, despite the correlation, there is no causal edge from A to B.
These observations imply that it is essential to undertake careful empirical assessment in order to learn whether computational methods can provide causal insights in specific biological settings. Network inference methods are often assessed using data simulated from a known causal network structure (a so-called gold-standard network5,17). Such studies (and their synthetic biology counterparts21) are convenient and useful, but at the same time they are limited because it is difficult to truly mimic specific biological systems of interest. Inferred networks are often compared to the literature, but for the purpose of learning novel, potentially context-specific, regulatory relationships, this is an inherently limited approach, and experimental validation of network inference methods has remained limited9,10,19,22.
With the support of the Heritage Provider Network (HPN), we developed the HPN-DREAM challenge to assess the ability to learn causal networks and predict molecular time-course data. The Dialogue for Reverse Engineering Assessment and Methods (DREAM) project23 (http://dreamchallenges.org) has run several challenges focused on network inference22,24,25,26,27. Here we focused on causal signaling networks in human cancer cell lines. Protein assays were carried out using reverse-phase protein lysate arrays28,29 (RPPAs) that included functional phosphorylated proteins.
The HPN-DREAM challenge comprised three sub-challenges. Sub-challenge 1 was to infer causal signaling networks using protein time-course data. To focus on networks specific to genetic and epigenetic background, the task spanned 32 different contexts, each defined by a combination of cell line and stimulus, and each with its own training and test data. The test data were used to assess the causal validity of inferred networks, as described below. A companion in silico data task also focused on causal networks but by design did not allow the use of known biology. Sub-challenge 2 was to predict phosphoprotein time-course data under perturbation. This sub-challenge comprised both an experimental data task and an in silico data task, and the same training data sets were used as in sub-challenge 1. Sub-challenge 3 was to develop methods to visualize these complex, multidimensional data sets.
Across all sub-challenges, the scientific community contributed 178 submissions. In the network inference sub-challenge we found that several submissions achieved statistically significant results, providing substantive evidence that causal network inference may be feasible in a complex, mammalian setting (we discuss a number of relevant caveats below). The use of pre-existing biological knowledge (e.g., from online databases) seemed to be broadly beneficial. However, FunChisq, a method that did not incorporate any known biology whatsoever, was not only the top performer in the in silico data task but also highly ranked in the experimental data task.
Challenge data, submissions and code have been made available as a community resource through the Synapse platform30, which was used to run the challenge (https://www.synapse.org/HPN_DREAM_Network_Challenge; methods applied in the challenge are described in Supplementary Notes 1–3).
Results
Experimental training data
For the experimental data network inference task, participants were provided with RPPA phosphoprotein data from four breast cancer cell lines under eight ligand stimulus conditions31. The 32 (cell line, stimulus) combinations each defined a biological context. Data for each context comprised time courses for ∼45 phosphoproteins (Supplementary Table 1). The training data included time courses obtained under three kinase inhibitors and a control (dimethyl sulfoxide (DMSO)) (Fig. 2a; details of the experimental design, protocol, quality control and pre-processing can be found in the Online Methods). The data set is also available in an interactive online platform (http://dream8.dibsbiotech.com) that uses the Biowheel design developed by the winning team of the visualization sub-challenge.
(a) Protein data were obtained from four cancer cell lines under eight stimuli (described in ref. 31). For each of the 32 resulting contexts, participants were provided with training data comprising time courses for ∼45 phosphoproteins under three different kinase inhibitors and a control (DMSO). For the sub-challenge 1 experimental data task (SC1A), participants were asked to infer causal signaling networks specific to each context. In SC2A, the aim was to predict context-specific phosphoprotein time courses. In both cases, submissions were assessed using held-out, context-specific test data that were obtained under an unseen intervention (inhibition of the kinase mTOR). Each sub-challenge also included a companion in silico data task (SC1B and SC2B, respectively; described in the text, Online Methods and Supplementary Fig. 1). Abund., abundance; TP, true positives; FP, false positives. (b) Networks submitted for SC1A were assessed causally in terms of agreement with the interventional test data. For each context, the set of nodes that changed under mTOR inhibition was identified (gold-standard causal descendants of mTOR; described in the text and Online Methods). In the example shown, node X is a descendant of mTOR, whereas node Y is not. (c) Predicted descendants of mTOR from submitted context-specific networks were compared with their experimentally determined gold-standard counterparts. This gave true and false positive counts and a (context-specific) AUROC. (d) In each context, teams were ranked by AUROC score, and mean rank across contexts gave the final rankings.
Participants were tasked with using the training data to learn causal networks specific to each of the 32 contexts. Networks had to comprise nodes corresponding to each phosphoprotein with directed edges between the nodes. The edges were required to have weights indicating the strength of evidence in favor of each possible edge, but they did not need to indicate sign (i.e., whether activating or inhibitory). For the companion in silico data task, participants were provided with data generated from a nonlinear differential equation model of signaling12. The task was designed to mirror some of the key features of the experimental setup, and participants were asked to infer a single directed, weighted network (Online Methods and Supplementary Fig. 1). Whereas the experimental data task tested both data-driven learning and use of known biology, the in silico data task focused exclusively on the former, and for that reason node labels (i.e., protein names in the underlying model) were anonymized.
Empirical assessment of causal networks
An incorrect causal network can score very well on standard statistical assessments of goodness of fit or predictive ability; for example, two nodes that are highly correlated but not causally linked (Fig. 1d) may predict each other well. For the experimental data task, we therefore developed a procedure that leveraged interventional data to assess inferred networks in a causal sense. The key idea was to assess the extent to which causal relationships encoded in inferred networks agreed with test data obtained under an unseen intervention (Fig. 2a). Specifically, for a given context c, we identified the set of nodes that showed salient changes under a test inhibitor (here an mTOR inhibitor) relative to the DMSO-treated control (Fig. 2b and Online Methods). These nodes can be regarded as descendants of the inhibitor target (mTOR) in the underlying causal network for context c. We denote this gold-standard descendant set by  (Supplementary Fig. 2). Note that
(Supplementary Fig. 2). Note that  may include both downstream nodes and those influenced via feedback loops within the experimental time frame. We emphasize that these 'gold-standard' sets are derived from (held-out) experimental data and should not be regarded as representing a fully definitive ground truth.
may include both downstream nodes and those influenced via feedback loops within the experimental time frame. We emphasize that these 'gold-standard' sets are derived from (held-out) experimental data and should not be regarded as representing a fully definitive ground truth.
For each submitted context-specific network, we computed a predicted set of mTOR descendants ( ) and compared it with
) and compared it with  to obtain an area under the receiver operating characteristic curve (AUROC) score (Fig. 2c). Teams were ranked in each of the 32 contexts by AUROC score, and the mean rank across contexts was used to provide an overall score and final ranking (Online Methods, Fig. 2d and Supplementary Fig. 3a). We tested the robustness of the rankings using a subsampling strategy (Online Methods). In addition to mean ranks, we used mean AUROC scores (across the contexts) in the analyses described below; these scores complement the mean ranks by giving information on the absolute level of performance, and the two metrics are highly correlated (Supplementary Fig. 3c).
to obtain an area under the receiver operating characteristic curve (AUROC) score (Fig. 2c). Teams were ranked in each of the 32 contexts by AUROC score, and the mean rank across contexts was used to provide an overall score and final ranking (Online Methods, Fig. 2d and Supplementary Fig. 3a). We tested the robustness of the rankings using a subsampling strategy (Online Methods). In addition to mean ranks, we used mean AUROC scores (across the contexts) in the analyses described below; these scores complement the mean ranks by giving information on the absolute level of performance, and the two metrics are highly correlated (Supplementary Fig. 3c).
For the in silico data task, the true causal network was known (Online Methods and Supplementary Fig. 4) and was used to obtain an AUROC score for each participant that determined the final rankings (Supplementary Fig. 3b).
An alternative scoring metric to AUROC is the area under the precision-recall curve (AUPR), which is often used when there is an imbalance between the number of positives and negatives in the gold standard32. Some of our settings were imbalanced, and we therefore compared rankings based on the AUROC and AUPR, which showed reasonable agreement (Online Methods and Supplementary Figs. 5 and 6).
Performance of individual teams and ensemble networks
Across the 32 contexts included in the experimental data network inference task (Fig. 3a), a mean of 11.8 teams (s.d. = 7.3; Supplementary Fig. 7 includes a full set of counts by context) achieved statistically significant AUROC scores (FDR < 0.05; multiple testing correction performed within each context with respect to the number of teams; Online Methods). For the in silico data task, the top 14 teams achieved significant AUROC scores (Supplementary Fig. 3b). The fact that several teams achieved significant scores with respect to causal performance metrics suggests that causal network inference may be feasible in this setting. Supplementary Table 2 presents a summary of submissions.
(a) AUROC scores in each of the 32 (cell line, stimulus) contexts for the 74 teams that submitted networks for the experimental data task. (b) Scores in experimental and in silico data tasks. Each square represents a team. Red borders around squares indicate that a different method was used in each task. Numbers adjacent to squares indicate ranks for the top ten teams under a combined score (three teams ranked third). (c,d) Results of crowdsourcing for the experimental data task. Aggregate networks were formed by combining, for each context, networks from top scoring (c) or randomly selected (d) teams (Online Methods). Dashed lines indicate aggregations of all submissions. Results in d are mean values over 100 iterations of random selection (error bars indicate ±s.d.). (e,f) Performance by method type for the experimental (e) and in silico (f) data tasks. The final rank is shown above each bar, and the gray lines indicate the mean performance of random predictions. ODE, ordinary differential equation.
Scores on the experimental data and in silico data network inference tasks were modestly correlated (r = 0.35, P = 0.011) but were better correlated when only teams that did not use prior information were compared (r = 0.68, P = 0.002; Fig. 3b and Supplementary Note 4). To identify teams that performed well across both tasks, we averaged ranks for experimental and in silico data tasks (Fig. 3b and Supplementary Fig. 3d).
To test the notion of 'crowdsourcing'22,27,33,34 for causal network inference, we combined inferred networks across all teams (Online Methods, Fig. 3c and Supplementary Fig. 8a). For the experimental data task, this ensemble or aggregate submission slightly outperformed the highest-ranked individual submission (mean AUROCs of 0.80 and 0.78, respectively), and for the in silico data task it ranked within the top five (AUROC of 0.67). Combinations of as few as 25% of randomly chosen submissions performed well on average (mean AUROCs of 0.72 and 0.64 for experimental and in silico data tasks, respectively; Fig. 3d and Supplementary Fig. 8b).
Methodological details were provided by 41 of the 80 participating teams (Supplementary Note 1), allowing us to classify submissions (Fig. 3e,f, Supplementary Table 2 and Supplementary Note 5). Similar to previous DREAM challenges22,33, we observed no clear relationship between method class and performance. We note that the boundaries between method classes are not always well defined and that additional factors, including details of pre-processing and implementation, can be important.
Top-performing methods for causal network inference
The best-scoring method for the experimental data task, “PropheticGranger with heat diffusion prior,” by Team1, used a prior network created by averaging similarity matrices. The matrices were obtained via simulated heat diffusion applied to links derived from the Pathway Commons database35. The prior network was then coupled with an L1-penalized regression approach that considered not only past but also future time points (a detailed description is presented in Supplementary Note 1). The best scoring approach for the in silico data network inference task, and the most consistent performer across both data types, was the FunChisq method by Team7 (Supplementary Note 1). This approach used a novel functional χ2 test to examine functional dependencies among the variables and did not use any biological prior information. Before FunChisq was applied, the abundance of each protein was discretized via the Ckmeans.1d.dp method36, with the number of discretization levels selected using the Bayesian information criterion on a Gaussian mixture model.
Incorporating pre-existing biological knowledge
On average, teams that used prior biological information outperformed those that did not (Fig. 4a; one-sided rank-sum test, P = 0.032). The submission ranked second used only a prior network and did not use the protein data. However, use of a prior network did not guarantee good performance, with mean AUROC scores ranging from 0.49 to 0.78 for teams using a prior network. Interestingly, the same prior network that was itself ranked second was used in both the top-performing submission and the submission ranked 43rd, the difference being the approach used to analyze the experimental data. Conversely, not using a prior network did not necessarily result in poor performance; mean AUROC scores ranged from 0.49 to 0.71 for teams not using a prior network. The top-performing teams using prior networks in the experimental data task did not perform as well in the in silico data task (Fig. 3b).
(a) Box plots showing mean AUROC scores for teams that either did or did not use a prior network. P value calculated via Wilcoxon rank-sum test (n = 18). (b) Performance of aggregate prior network when combined with networks inferred by PropheticGranger (top performer in SC1A when combined with a network prior) or FunChisq (top performer in SC1B). The blue line indicates aggregate prior combined with randomly generated networks (mean of 30 random networks; shading indicates ±s.d.). The dashed line shows the mean AUROC score achieved by the top-performing team in SC1A. Error bars denote ±s.e.m. (c) Performance of aggregate submission network and aggregate prior network in each context. Top, performance by context. Box plots over AUROC scores for the top 25 performers for each context, shown for comparison. Bottom, receiver operating characteristic curves for two contexts that showed performance differences between aggregate submission and prior. For all box plots, line within the box indicates the median, and the box edges denote the 25th and 75th percentiles. Whiskers extend to 1.5 times the interquartile range from the box hinge. Individual data points are also shown.
To further investigate the influence of known biology, we combined submitted prior networks to form an aggregate prior network (Online Methods). This outperformed the individual prior networks and had a score similar to that of the aggregate submission described above (mean AUROC of 0.79). We combined the aggregate prior network with each of the two top methods (PropheticGranger and FunChisq) in varying proportions (Fig. 4b). Combining FunChisq with the aggregate prior improved upon the aggregate prior alone (this was not the case for PropheticGranger). Finally, we considered three-way combinations of PropheticGranger, FunChisq and the aggregate prior; the highest-scoring combination consisted of 20% PropheticGranger, 50% FunChisq and 30% aggregate prior (mean AUROC of 0.82; Supplementary Fig. 9). We set the combination weights by optimizing performance on the test data; we note that because additional test data were not available, we could not rigorously assess the combination analyses.
Context-specific performance
The overall score in the experimental data task was an average over all contexts; to gain additional insight, we further investigated performance by context. In line with their good overall performance, aggregate submission and prior performed well relative to individual submissions in most contexts (Fig. 4c). The aggregate prior network performed particularly well for cell line MCF7 but less well for BT549, supporting the notion that biological contexts differ in the extent to which they agree with known biology. The aggregate submission offered the greatest improvements over the aggregate prior in settings where the aggregate prior performed less well, suggesting that combining data-driven learning with known biology might offer the most utility in noncanonical settings.
Crowdsourced context-specific signaling hypotheses
The context-specific aggregate submission networks (see Fig. 5a for an example) provided crowdsourced signaling hypotheses. Comparing the aggregate submission with the aggregate prior network helped to highlight potentially novel edges; we have provided a list of context-specific edges with their associated scores as a resource (Supplementary Table 3). Dimensionality reduction suggested that differences between cell lines were more prominent than those between stimuli for a given cell line (Fig. 5b and Online Methods), in line with the notion that (epi)genetic background has a key role in determining network architecture.
(a) The aggregate submission network for cell line MCF7 under HGF stimulation. Line thickness corresponds to edge weight (number of edges shown set to equal number of nodes). To determine which edges were present and not present in the aggregate prior network, we placed a threshold of 0.1 on edge weights. Green and blue nodes represent descendants of mTOR in the network shown (Fig. 2b,c and Supplementary Fig. 2). The network was generated using Cytoscape40. (b) Principal component analysis applied to edge scores for the 32 context-specific aggregate submission networks (Online Methods).
Time-course prediction sub-challenge
In the time-course prediction sub-challenge, participants predicted phosphoprotein time courses obtained under interventions not seen in the training data (Online Methods). We assessed predictions by direct comparison with the test data using root-mean-square (r.m.s.) error (Online Methods and Supplementary Note 6), focusing on predictive ability rather than causal validity. Supplementary Table 4 and Supplementary Note 2 present team scores and descriptions of submissions. Testing the robustness of team ranks gave two top performers for the experimental data task and a single top performer for the in silico data task (Online Methods).
The two top performers for the experimental data task took different approaches. Team42 (ranked second) simply calculated averages of values in the training data. Team10 (ranked third) used a truncated singular value decomposition to estimate parameters in a regression model. This method also ranked highly for the in silico data task and was the most consistent performer across both data types. Team44, the top-ranked team, was not eligible to be named as a top performer because of an incomplete submission (Supplementary Note 7), but their approach also consisted of calculating averages. The good performance of averaging may be explained to some degree by a shortcoming with the r.m.s. error metric used here (Supplementary Fig. 10). Team34, the top performer for the in silico data task, used a model informed by networks learned in the network inference sub-challenge. This suggests that networks can also have a useful role in purely predictive analyses.
Visualization sub-challenge
A total of 14 teams submitted visualizations that were made available to the HPN-DREAM Consortium members, who then voted for their favorite (Online Methods). The winning entry, Biowheel, is designed to enhance the visualization of time-course protein data and aid in their interpretation (Supplementary Note 3). The data associated with a cell line are plotted to depict protein-abundance levels by color, as in a heat map, but are displayed as a ring, or wheel. Time is plotted along the radial axis and increases from the center outward. The interactive tool provides a way to mine data by displaying data subsets in various ways.
Discussion
Inferring molecular networks remains a key open problem in computational biology. This study was motivated by the view that empirical assessment will be essential in catalyzing the development of effective methods for causal network inference. Such methods will be needed to systemically link molecular networks to the phenotypes they influence. Although causal network inference may fail for many theoretical and practical reasons, our results, obtained via a large-scale, community effort with blinded assessment, suggest that the task may be feasible in complex mammalian settings. By “feasible,” we mean capable of reaching a performance level significantly better than that achieved by chance, and this was accomplished by a number of submissions, including approaches that did not use any prior information.
Our assessment approach focuses on causal validity and is general enough to be applicable in a variety of settings, such as gene regulatory or metabolic networks. However, it is important to take note of several caveats. First, the procedure relies on the specificity of test inhibitors. However, if the inhibitor were highly nonspecific, it would probably not be possible to achieve good results or for a prior network to perform well, because the predictions themselves are based on assumed specificity. In addition, data suggest that the mTOR inhibitor used here is reasonably specific37. Second, the procedure used only one of the inhibitors for testing, whereas rankings could be changed by the inclusion of additional inhibitors. Hill et al.31 used a cross-validation–type scheme that iterated over inhibitors. Such an approach, although more comprehensive, is not possible in a 'live' challenge setting, as training and test data must be fixed at the outset. Third, the procedure does not distinguish between direct and indirect causal effects. Finally, all downstream nodes were weighted equally, regardless of whether they were context specific. Metrics that better emphasize context-specific effects will be an important avenue for future research and would probably shed further light on the utility of priors (which are not usually context specific). We also emphasize that further work is needed to clarify the theoretical properties of the score used here with respect to capturing agreement with the (unknown) ground truth.
Several submissions used novel methods or incorporated novel adaptations of existing methods (Supplementary Tables 2 and 4). Notably, the best-performing team for the network inference in silico data task developed a novel procedure (FunChisq) that also performed well on the experimental data task without use of prior information, increasing confidence in its robustness. Indeed, the ability to make such comparisons is a key benefit of running experimental and in silico challenges in parallel. Although some approaches performed well on one data type only (Fig. 3b), the overall positive correlation between experimental and in silico scores is striking given that they were based on different data and assessment metrics. Teams that did not use prior information were relatively well correlated (Fig. 3b), suggesting that good performers among these teams on the in silico data task could perform competitively on experimental data if their methods were extended to incorporate known biology.
The observation that prior information alone performs well reflects the fact that much is already known about signaling in cancer cells and suggests that causal networks are not entirely 'rewired' in those cells. However, our analysis revealed contexts that deviate from known biology; such deviations are likely to be particularly important for understanding disease-specific dysregulation and therapeutic heterogeneity. Furthermore, it is possible that the literature is biased toward cancer, and for that reason priors based on the literature may be less effective in other disease settings. We anticipate that in the future a combination of known biology and data-driven learning will be important in elucidating networks in specific disease states.
A previous DREAM challenge also focused on signaling networks in cancer26. However, the scoring metric was predictive rather than causal (r.m.s. error between predicted and test data points) with a penalty related to sparseness of the inferred network. Our assessment approach shares similarities with other approaches in the literature, including those used by Maathuis et al.38, who focused on inferring networks from static observational data, and Olsen et al.39, who used a different scoring metric, considering predicted downstream targets in close network proximity to the inhibited node.
It remains unclear to what extent the ranking of specific submitted methods could be generalized to different data types and biological processes. In our view, it is still too early to say whether there could emerge broadly effective 'out-of-the-box' methods for causal network inference analogous to methods used for some tasks in statistics and machine learning. Given the complexity of causal learning and the wide range of application-specific factors, we recommend that at the present time network inference efforts should whenever possible include some interventional data and that suitable scores, such as those described in this paper, be used for empirical assessment in the setting of interest.
Methods
Challenge data.
The HPN-DREAM network inference challenge comprised three sub-challenges: causal network inference (SC1), time-course prediction (SC2) and visualization (SC3). SC1 and SC2 each consisted of two tasks, one based on experimental data (SC1A and SC2A, respectively) and the other based on in silico data (SC1B and SC2B, respectively).
Experimental data. The experimental data and associated components of the challenge are outlined in Figure 2a. Protein data from four breast cancer cell lines (UACC812, BT549, MCF7 and BT20) were provided for the challenge. All cell lines were acquired from ATCC, authenticated by short tandem repeat (STR) analysis, and tested for mycoplasma contamination. These cell lines were chosen because they represent the major subtypes of breast cancer (basal, luminal, claudin-low and HER2-amplified) and are known to have different genomic aberrations41,42,43. Each cell line sample was treated with one of eight stimuli (serum, PBS, EGF, insulin, FGF1, HGF, NRG1 and IGF1). We refer to each of the 32 possible combinations of cell line and stimulus as a biological context. For each context, data consisted of time courses for total proteins and post-translationally modified proteins, obtained under four different kinase inhibitors and a DMSO control. Full details of sample preparation, data generation, quality control and pre-processing steps can be found in ref. 31 and on the Synapse30 webpage describing the challenge (https://www.synapse.org/HPN_DREAM_Network_Challenge). In brief, cell lines were serum-starved for 24 h and then treated for 2 h with an inhibitor (or combination of inhibitors) or DMSO vehicle alone. Cells were then either harvested (0 time point) or stimulated by one of the eight stimuli for 5, 15, 30 or 60 min or for 2, 4, 12, 24, 48 or 72 h before protein harvest and analysis by RPPA at the MD Anderson Cancer Center Functional Proteomics Core Facility (Houston, Texas).
RPPA is an antibody-based assay that provides quantitative measurements of protein abundance28,44. The MD Anderson RPPA core facility maintains and updates a standard antibody list on the basis of antibody quality control as well as a variety of other factors, including scientific interest. Antibodies available for use in this assay are therefore enriched for components of receptor tyrosine kinase signaling networks and cancer-related proteins. For each cell line, we used the standard antibody list available at the time the assays were performed. We used 183 antibodies to target total (n = 132), cleaved (n = 3) and phosphorylated (n = 48) proteins (the set of phosphoproteins varied slightly between cell lines; Supplementary Table 1). As part of the RPPA pipeline, we performed quality control to identify slides with poor antibody staining. Antibodies with poor quality control scores were excluded from the data set. During the challenge period, it became known to challenge organizers that several antibodies were of poor quality. Participants were advised not to include the associated data in their analyses, and these data were excluded from the scoring process. Measurements for each sample were corrected for protein loading, and several outlier samples with large correction factors were identified and removed. The UACC812 data were split across two batches. A batch-normalization procedure was applied31 to enable the data from the two batches to be combined. The experimental data used in the challenge are a subset of the data reported by Hill et al.31.
The inhibitors were chosen because they target key components of the receptor tyrosine kinase signaling cascades assessed by the RPPA and are also relevant to breast cancer. Participants were provided with a training data set consisting of data for four out of the five inhibitor regimes (DMSO, PD173074 (FGFRi), GSK690693 (AKTi), and GSK690693 + GSK1120212 (AKTi + MEKi)). Note that there were no training data available for the AKTi + MEKi inhibitor regime for cell lines BT549 (all stimuli) and BT20 (PBS and NRG1 stimuli). Data for the remaining inhibitor (AZD8055 (mTORi)) formed a test data set, unseen by participants and used to evaluate submissions to the challenge.
The focus of the challenge was on short-term phosphoprotein signaling events and not on medium- to long-term changes over hours and days (for example, rewiring of networks due to epigenetic changes arising from prolonged exposure to an inhibitor). Therefore the training data consisted only of phosphoprotein data (∼45 phosphoproteins for each cell line) up to and including the 4-h time point; in the challenge this data set was referred to as the main data set. In case some participants found the additional data useful, measurements for the remaining antibodies and time points were also made available in a 'full' data set. The test data (and challenge scoring) also focused only on phosphoproteins up to and including the 4-h time point. At the time of the challenge, all data were unpublished (the training data set was made available to participants through the Synapse platform).
In silico data. The in silico data and associated components of the challenge are outlined in Supplementary Figure 1. Simulated data were generated from a nonlinear ordinary differential equation (ODE) model of the ERBB signaling pathway. Specifically, the model was an extended version of the mass action kinetics model developed by Chen et al.12. Training data were simulated for 20 network nodes (Supplementary Fig. 4; 14 phosphoproteins, two phospholipids, GTP-bound RAS and three dummy nodes that were unconnected in the network) under two ligand stimuli (each at two concentrations; applied individually and in combination) and under three inhibitors targeting specific nodes in the network or no inhibitor. Mirroring the experimental data, inhibitors were applied before ligand stimulation at t = 0. Time courses consisted of 11 time points (0, 1, 2, 4, 6, 10, 15, 30, 45, 60 and 120 min), and three technical replicates were provided for each sample. A measurement error model was developed to reflect the antibody-based readout of RPPAs and its technical variability. Node names were anonymized to prevent the use of prior information to trivially reconstruct the network. Further details of the simulation model can be found in Supplementary Note 8.
An in silico test data set was also generated to assess submissions to the time-course prediction sub-challenge and consisted of time courses for each node and stimulus, under in silico inhibition of each network node in turn. After the final team rankings for the in silico data task were calculated, two minor issues concerning the in silico test data were discovered. The issues were corrected, test data were regenerated, and final rankings and final leaderboards were updated. The top-performing teams remained unchanged after this update. Further details can be found in Supplementary Note 8.
Challenge questions and design.
For the network inference sub-challenge experimental data task, participants were asked to use the training data to learn 32 signaling networks, one for each of the (cell line, stimulus) contexts. Networks had to contain nodes for each phosphoprotein in the training data (node sets therefore varied depending on cell line), and network edges had to be directed (but unsigned). The networks were expected to describe causal edges, and this was reflected in the scoring (discussed below). A causal edge was defined as one for which inhibition of the parent node can result in a change in the abundance of the child node that is not fully mediated via any other measured node (but the influence can take place via unmeasured nodes; Fig. 1). Participants were asked to submit confidence scores (between 0 and 1) for each possible directed edge in each network. Node names were not anonymized for the experimental data task, and participants were allowed to use pre-existing biological information (e.g., from literature and online databases) in their analyses.
For the network inference sub-challenge in silico data task, participants were asked to infer a single network with 20 nodes (one for each variable in the training data) and directed edges corresponding to predicted causal relationships between the nodes. Submissions comprised a set of confidence scores for each possible directed edge in the network.
For the time-course prediction sub-challenge, participants were tasked with predicting time courses under interventions not contained in the training data set. For the experimental data task, predictions were requested for five test kinase inhibitors (participants were informed of the inhibitor targets). For each inhibitor, time courses consisting of seven time points (as in the training data) had to be predicted for each of the 32 contexts and for all phosphoproteins (except those targeted by the inhibitor). The in silico data task proceeded in an analogous fashion, with participants asked to predict time courses under inhibition of each of the 20 nodes in turn. Predicted time courses were required for each node for each of the eight stimulus contexts.
In the visualization sub-challenge, participants were asked to devise novel approaches to represent the data set provided with the challenge. The submission format was a schematic mock-up of the visualization.
The challenge was run over a period of 3 months. For the network inference and time-course prediction sub-challenges, participants were able to make submissions and obtain feedback via a leaderboard on a weekly basis (Supplementary Note 9). The frequency of feedback was chosen so as to obtain a balance between actively engaging participants and avoiding overfitting of models to the test data. To address this overfitting issue, other DREAM challenges34,45 used a second held-out test data set for final scoring of submissions. However, this was not possible here because of the small number of inhibitor conditions in the data.
As an incentive for participation, top-performing teams were awarded a modest cash prize (provided by HPN), invitations to present results at a conference and coauthor the paper describing the challenge, and (for SC1A only) the opportunity to have their method developed as a Cytoscape Cyni app39,46. Further details can be found on the Synapse web pages describing the challenge (https://www.synapse.org/HPN_DREAM_Network_Challenge) and in Supplementary Note 7.
Scoring procedure for the network inference sub-challenge experimental data task.
Interventional test data. For the experimental data task, we developed a scoring procedure that used held-out interventional data to assess the causal validity of networks submitted by participants. The procedure assessed the extent to which causal relationships encoded in network submissions agreed with causal information contained in the test data. Using the held-out mTOR inhibitor data, we identified those phosphoproteins that showed a salient change in abundance under the inhibitor relative to the DMSO-treated control (Fig. 2b). Specifically, we let  and
and  denote the mean abundance levels of phosphoprotein i for (cell line, stimulus) context c under DMSO control conditions and mTOR inhibition, respectively (mean values were calculated over seven time points on log-transformed data; any replicates at each time point were averaged before the mean was taken). A paired t-test was used to assess whether
denote the mean abundance levels of phosphoprotein i for (cell line, stimulus) context c under DMSO control conditions and mTOR inhibition, respectively (mean values were calculated over seven time points on log-transformed data; any replicates at each time point were averaged before the mean was taken). A paired t-test was used to assess whether  was significantly different from
was significantly different from  , resulting in a P value pic for each phosphoprotein and context.
, resulting in a P value pic for each phosphoprotein and context.
Some phosphoproteins show a clear stimulus response under DMSO, characterized by a marked increase and subsequent decrease in abundance over time (a 'peak' shape). In such cases, a change in abundance due to the mTOR inhibitor may be observable only at intermediate time points. Because the paired t-test described above considers all time points, this effect may be masked. Therefore we used a heuristic to detect phosphoproteins with a peak-shaped time course under DMSO and re-performed the paired t-test over the intermediate time points within the peak only. The resulting P value was retained if smaller than the original. For each context, a test was performed for each phosphoprotein. We corrected for multiple testing within each context using the median adaptive linear step-up procedure47, which resulted in q-values (FDR-adjusted P values) qic. Note that owing to the heuristic step, qic should not be interpreted formally.
For each context, a phosphoprotein was determined to have shown a change under the mTOR inhibitor if the following two conditions were satisfied: (1) qic < 0.05 and (2)  , where σi,c is the pooled replicate s.d. for the DMSO and mTOR inhibitor data. The second condition acted as a conservative filter to ensure that effect sizes were not small relative to replicate variation. We worked under the assumption that mTOR inhibition would lead to changes in the abundance of all descendants of mTOR in the underlying context-specific causal network (i.e., that changes would be observed in any node for which a directed path existed from mTOR to that node; this included downstream nodes as well as those influenced via feedback loops within the timescale of the experiments). This procedure resulted in context-specific gold-standard sets of causal descendants of mTOR
, where σi,c is the pooled replicate s.d. for the DMSO and mTOR inhibitor data. The second condition acted as a conservative filter to ensure that effect sizes were not small relative to replicate variation. We worked under the assumption that mTOR inhibition would lead to changes in the abundance of all descendants of mTOR in the underlying context-specific causal network (i.e., that changes would be observed in any node for which a directed path existed from mTOR to that node; this included downstream nodes as well as those influenced via feedback loops within the timescale of the experiments). This procedure resulted in context-specific gold-standard sets of causal descendants of mTOR  (Supplementary Fig. 2).
(Supplementary Fig. 2).
The scoring metric. For each context c, we compared the gold-standard descendant set  (obtained from the held-out test data) with predicted descendant sets obtained from context-specific networks submitted by participants (Fig. 2c). For context c, a submitted network consisted of edge confidence scores for each possible directed edge. Placing a threshold τ on edge scores resulted in a network structure consisting only of those edges with a score greater than τ, and from this network we obtained a predicted set of descendants of mTOR (at threshold τ), denoted by
(obtained from the held-out test data) with predicted descendant sets obtained from context-specific networks submitted by participants (Fig. 2c). For context c, a submitted network consisted of edge confidence scores for each possible directed edge. Placing a threshold τ on edge scores resulted in a network structure consisting only of those edges with a score greater than τ, and from this network we obtained a predicted set of descendants of mTOR (at threshold τ), denoted by  . Comparing
. Comparing  with
with  gave the number of predicted descendants that were correct (true positives; TP (τ)) and the number of predicted descendants that were incorrect (false positives; FP(τ)). Varying the threshold τ and plotting TP(τ) against FP(τ) resulted in a receiver operating characteristic curve, and the scoring metric was the area under this curve (normalized to be between zero and one; AUROC). For each team, AUROC scores were calculated for each of the 32 contexts.
gave the number of predicted descendants that were correct (true positives; TP (τ)) and the number of predicted descendants that were incorrect (false positives; FP(τ)). Varying the threshold τ and plotting TP(τ) against FP(τ) resulted in a receiver operating characteristic curve, and the scoring metric was the area under this curve (normalized to be between zero and one; AUROC). For each team, AUROC scores were calculated for each of the 32 contexts.
The statistical significance of AUROC scores was determined using simulated null distributions, generated by calculating AUROC scores for 100,000 random networks, each consisting of random edge scores (drawn independently from the uniform distribution on the unit interval [0,1]). Gaussian fits to the null distributions were used to calculate P values. For each context, the set of P values (across all teams) underwent multiple testing correction using the Benjamini-Hochberg FDR procedure. There were two contexts (BT549, NRG1 and BT20, insulin) for which no team achieved a statistically significant (FDR < 0.05) AUROC score (Supplementary Fig. 7b). These two contexts were therefore regarded as too challenging and were disregarded in the scoring procedure.
Teams were ranked in each context according to AUROC score. The resulting 30 rank scores for each team were then averaged to obtain a mean rank score. Final team rankings were obtained using mean rank scores (Fig. 2d).
During the challenge period, participants were informed only that submitted networks would be scored using test data obtained under interventions not present in the training data; details of the scoring procedure and the identity, nature and number of interventions in the test data were not revealed. Note that participants knew the identities of inhibitors in the training data.
Gold-standard network and scoring metric for the network inference sub-challenge in silico data task.
The true causal network underlying the variables in the in silico data was obtained from the data-generating nonlinear ODE model (Supplementary Fig. 4). However, deriving the causal network from the equations was not trivial because the model contained more variables than the 20 variables present in the challenge data and some variables appeared in the model in complexes. Details of how the causal network was obtained can be found in Supplementary Note 8.
Each team submitted a single network consisting of a set of edge scores. This was compared directly to the gold-standard causal network to produce a receiver operating characteristic curve (by calculating the number of true positive and false positive edges at various edge score thresholds), and the AUROC was used as the scoring metric. Self-edges were not considered for scoring. The statistical significance of AUROC scores was determined analogously to the experimental data task.
Alternative scoring metrics for the network inference sub-challenge.
We used AUROC as the scoring metric for the network inference sub-challenge, but we note that alternative metrics could have been used. In particular, the AUPR is often used when there is an imbalance between the number of positives and negatives in the gold standard32. Although many contexts in the experimental data task had a reasonable balance (median ratio of negatives to positives of 1.71), some contexts had many more negatives than positives, and there was also an imbalance for the in silico data task (ratio of negatives to positives of 4.14; Supplementary Fig. 5). Therefore AUPR could have been an appropriate choice in several cases. For this reason, at the end of the challenge period we performed comparisons of final team rankings (obtained using AUROC) to rankings obtained using AUPR or a combination of AUROC and AUPR (Supplementary Fig. 6). For the experimental data task, the AUROC-based rankings showed good agreement with those obtained under either alternative metric. Agreement was not as strong for the in silico data task, but it was still reasonable, with all metrics resulting in the same top performer. Furthermore, of the top ten teams under AUROC, only two were outside the top ten under AUPR, and they ranked 12th and 13th. Similarly, only two of the top ten teams under AUPR were not in the top ten under AUROC, and they ranked 11th and 12th. For openness and transparency, scores and rankings based on AUPR and the combination metric were included in the final leaderboards (available through Synapse at https://www.synapse.org/HPN_DREAM_Network_Challenge; combination metric scores are also included in Supplementary Table 2).
Scoring metric for the time-course prediction sub-challenge.
For both experimental data and in silico data, predictions of context-specific time courses under inhibitors not contained in the training data were directly compared against context-specific test data obtained under the corresponding inhibitor. Prediction accuracy was quantified using r.m.s. error with comparisons made on log-transformed data after averaging of replicates. The r.m.s. error scores were calculated separately for parts of the data that could potentially be on different scales. We refer to each portion of the data where an r.m.s. error score was calculated as a 'data block'. Teams were ranked within each data block, and a mean rank was calculated to obtain a final ranking. Some blocks of data, where no team achieved a statistically significant score, were disregarded in the scoring procedure (Supplementary Tables 5 and 6; FDR < 0.05). Full details of the scoring are presented in Supplementary Note 6.
Visualization sub-challenge scoring.
HPN-DREAM challenge participants scored submitted visualization proposals. Thirty-six participants cast votes by assigning ranks (from 1 to 3) to their three favorite submissions (the remaining submissions were all assigned a rank of 4). Teams were then ranked according to mean rank across the 36 votes (Supplementary Fig. 11).
Robustness of ranking under subsampling.
To ensure that team rankings were robust in the network inference and time-course prediction sub-challenges, we performed a subsampling analysis in which, for each of 100 iterations, 50% of the test data were removed at random and rankings of submissions were recalculated using the remaining test data. Team A was considered to be robustly ranked above team B if the former outranked the latter in at least 75% of iterations.
For the network inference sub-challenge experimental data task, we subsampled test data by either (i) removing 50% of the phosphoproteins for each (cell line, stimulus) context when making comparisons between gold-standard and predicted descendant sets (Supplementary Fig. 12a) or (ii) removing 50% of the contexts (i.e., scoring was based on 15 contexts instead of 30; Supplementary Fig. 12b). The top team (Team1) outranked the team ranked second (Team2) in 76% and 97% of iterations for subsampling methods i and ii, respectively. For the network inference sub-challenge in silico data task, 50% of the edges (and non-edges) in the gold-standard network were used for scoring (Supplementary Fig. 12c). The top-scoring performer (Team7) had a higher AUROC score than the team ranked second (Team11) in 89% of the subsampling iterations.
For the experimental and in silico data tasks in the time-course prediction sub-challenge, we subsampled test data by either (i) removing 50% of the data blocks or (ii) subsampling 50% of the data points within each data block. For the experimental data task, the top-ranked team (Team44) outranked the team ranked second (Team42) in 90% and 54% of iterations for subsampling methods i and ii, respectively. Because the 75% threshold was not met for one of the subsampling methods, Team44 was not regarded as ranked robustly above Team42. Team42 outranked the team ranked third (Team10) in 60% and 70% of iterations and so, again, the ranking was not regarded as robust. However, Team10 was robustly ranked above the team ranked fourth (93% and 94% of iterations). Team44 was not eligible to be named as a top performer because of an incomplete submission (Supplementary Note 7), and so the teams ranked second and third (Team42 and Team10, respectively) were named as top performers. For the in silico data task, the top team (Team34) outranked the team ranked second in 95% and 100% of iterations for subsampling methods i and ii, respectively.
Crowdsourced analyses: aggregate submission networks and aggregate prior network.
We obtained aggregate submission networks by integrating predicted networks across all teams (to avoid bias, we used a filtering process to remove correlated submissions from the aggregation; 66 and 58 teams formed the aggregate networks for the experimental and in silico data tasks, respectively; Supplementary Note 10 and Supplementary Table 2). For the experimental data task, an aggregate network was formed for each of the 32 contexts. Each aggregate submission network consisted of a set of edge scores, calculated by taking the mean of scores submitted by teams for each edge. To ensure that edge scores were comparable across teams, we scaled scores for each team before aggregation so that the maximum edge score (across all 32 contexts for the experimental data task) had a value of one.
For the experimental data task, an aggregate prior network was formed in an analogous manner to the aggregate submission networks, using ten prior networks provided by teams (the prior network submitted by Team2 was also used by several other teams but was included only once in the aggregation; Supplementary Table 2). Individual prior networks, and therefore the aggregate prior network, were not context specific.
Principal component analysis of context-specific aggregate submission networks.
The 32 context-specific aggregate submission networks for the network inference sub-challenge experimental data task were combined into a matrix E of edge scores in which columns corresponded to contexts and rows corresponded to edges (only network nodes common to all contexts were considered for this analysis). Each row of matrix E contained the scores for a specific edge in each of the contexts. Principal component analysis was performed on this matrix using the MATLAB function princomp.
Web-based community resource.
A community resource has been made available through the Synapse platform at https://www.synapse.org/HPN_DREAM_Network_Challenge under the section titled “HPN-DREAM Community Resource.” This resource includes all challenge data, participant submissions, participant code, participant prior networks and crowdsourced aggregate networks. Code for scoring submissions is available as part of the DREAMTools software package48 (Supplementary Note 11).
Accession codes.
All data used for the challenge are available through Synapse under ID syn1720047.
References
Bansal, M., Belcastro, V., Ambesi-Impiombato, A. & di Bernardo, D. How to infer gene networks from expression profiles. Mol. Syst. Biol. 3, 78 (2007).
Markowetz, F. & Spang, R. Inferring cellular networks—a review. BMC Bioinformatics 8, S5 (2007).
Hecker, M., Lambeck, S., Toepfer, S., van Someren, E. & Guthke, R. Gene regulatory network inference: data integration in dynamic models—a review. Biosystems 96, 86–103 (2009).
De Smet, R. & Marchal, K. Advantages and limitations of current network inference methods. Nat. Rev. Microbiol. 8, 717–729 (2010).
Marbach, D. et al. Revealing strengths and weaknesses of methods for gene network inference. Proc. Natl. Acad. Sci. USA 107, 6286–6291 (2010).
Maetschke, S.R., Madhamshettiwar, P.B., Davis, M.J. & Ragan, M.A. Supervised, semi-supervised and unsupervised inference of gene regulatory networks. Brief. Bioinform. 15, 195–211 (2014).
Ideker, T. & Krogan, N.J. Differential network biology. Mol. Syst. Biol. 8, 565 (2012).
de la Fuente, A. From 'differential expression' to 'differential networking'—identification of dysfunctional regulatory networks in diseases. Trends Genet. 26, 326–333 (2010).
Hill, S.M. et al. Bayesian inference of signaling network topology in a cancer cell line. Bioinformatics 28, 2804–2810 (2012).
Saez-Rodriguez, J. et al. Comparing signaling networks between normal and transformed hepatocytes using discrete logical models. Cancer Res. 71, 5400–5411 (2011).
Molinelli, E.J. et al. Perturbation biology: inferring signaling networks in cellular systems. PLoS Comput. Biol. 9, e1003290 (2013).
Chen, W.W. et al. Input-output behavior of ErbB signaling pathways as revealed by a mass action model trained against dynamic data. Mol. Syst. Biol. 5, 239 (2009).
Akbani, R. et al. A pan-cancer proteomic perspective on The Cancer Genome Atlas. Nat. Commun. 5, 3887 (2014).
Eduati, F., De Las Rivas, J., Di Camillo, B., Toffolo, G. & Saez-Rodriguez, J. Integrating literature-constrained and data-driven inference of signalling networks. Bioinformatics 28, 2311–2317 (2012).
Pearl, J. Causality: Models, Reasoning, and Inference 2nd edn. (Cambridge Univ. Press, 2009).
Freedman, D. & Humphreys, P. Are there algorithms that discover causal structure? Synthese 121, 29–54 (1999).
Husmeier, D. Sensitivity and specificity of inferring genetic regulatory interactions from microarray experiments with dynamic Bayesian networks. Bioinformatics 19, 2271–2282 (2003).
Friedman, N., Linial, M., Nachman, I. & Pe'er, D. Using Bayesian networks to analyze expression data. J. Comput. Biol. 7, 601–620 (2000).
Sachs, K., Perez, O. & Pe'er, D. Causal protein-signaling networks derived from multiparameter single-cell data. Science 308, 523–529 (2005).
Spirtes, P., Glymour, C.N. & Scheines, R. Causation, Prediction, and Search 2nd edn. (MIT Press, 2000).
Cantone, I. et al. A yeast synthetic network for in vivo assessment of reverse-engineering and modeling approaches. Cell 137, 172–181 (2009).
Marbach, D. et al. Wisdom of crowds for robust gene network inference. Nat. Methods 9, 796–804 (2012).
Stolovitzky, G., Monroe, D. & Califano, A. Dialogue on reverse-engineering assessment and methods: the DREAM of high-throughput pathway inference. Ann. NY Acad. Sci. 1115, 1–22 (2007).
Stolovitzky, G., Prill, R.J. & Califano, A. Lessons from the DREAM2 challenges. Ann. NY Acad. Sci. 1158, 159–195 (2009).
Prill, R.J. et al. Towards a rigorous assessment of systems biology models: the DREAM3 challenges. PLoS ONE 5, e9202 (2010).
Prill, R.J., Saez-Rodriguez, J., Alexopoulos, L.G., Sorger, P.K. & Stolovitzky, G. Crowdsourcing network inference: the DREAM predictive signaling network challenge. Sci. Signal. 4, mr7 (2011).
Meyer, P. et al. Network topology and parameter estimation: from experimental design methods to gene regulatory network kinetics using a community based approach. BMC Syst. Biol. 8, 13 (2014).
Tibes, R. et al. Reverse phase protein array: validation of a novel proteomic technology and utility for analysis of primary leukemia specimens and hematopoietic stem cells. Mol. Cancer Ther. 5, 2512–2521 (2006).
Mertins, P. et al. Ischemia in tumors induces early and sustained phosphorylation changes in stress kinase pathways but does not affect global protein levels. Mol. Cell. Proteomics 13, 1690–1704 (2014).
Derry, J.M.J. et al. Developing predictive molecular maps of human disease through community-based modeling. Nat. Genet. 44, 127–130 (2012).
Hill, S.M. et al. Context-specificity in causal signaling networks revealed by phosphoprotein profiling. bioRxiv doi:10.1101/039636 (2016).
Davis, J. & Goadrich, M. The relationship between Precision-Recall and ROC curves. in Proc. 23rd International Conference on Machine Learning 233–240 (ACM, 2006).
Costello, J.C. et al. A community effort to assess and improve drug sensitivity prediction algorithms. Nat. Biotechnol. 32, 1202–1212 (2014).
Margolin, A.A. et al. Systematic analysis of challenge-driven improvements in molecular prognostic models for breast cancer. Sci. Transl. Med. 5, 181re1 (2013).
Cerami, E.G. et al. Pathway Commons, a web resource for biological pathway data. Nucleic Acids Res. 39, D685–D690 (2011).
Wang, H. & Song, M. Ckmeans.1d.dp: optimal k-means clustering in one dimension by dynamic programming. R J. 3, 29–33 (2011).
Chresta, C.M. et al. AZD8055 is a potent, selective, and orally bioavailable ATP-competitive mammalian target of rapamycin kinase inhibitor with in vitro and in vivo antitumor activity. Cancer Res. 70, 288–298 (2010).
Maathuis, M.H., Colombo, D., Kalisch, M. & Bühlmann, P. Predicting causal effects in large-scale systems from observational data. Nat. Methods 7, 247–248 (2010).
Olsen, C. et al. Inference and validation of predictive gene networks from biomedical literature and gene expression data. Genomics 103, 329–336 (2014).
Shannon, P. et al. Cytoscape: a software environment for integrated models of biomolecular interaction networks. Genome Res. 13, 2498–2504 (2003).
Neve, R.M. et al. A collection of breast cancer cell lines for the study of functionally distinct cancer subtypes. Cancer Cell 10, 515–527 (2006).
Garnett, M.J. et al. Systematic identification of genomic markers of drug sensitivity in cancer cells. Nature 483, 570–575 (2012).
Barretina, J. et al. The Cancer Cell Line Encyclopedia enables predictive modelling of anticancer drug sensitivity. Nature 483, 603–607 (2012).
Hennessy, B.T. et al. A technical assessment of the utility of reverse phase protein arrays for the study of the functional proteome in non-microdissected human breast cancers. Clin. Proteomics 6, 129–151 (2010).
Eduati, F. et al. Prediction of human population responses to toxic compounds by a collaborative competition. Nat. Biotechnol. 33, 933–940 (2015).
Guitart-Pla, O., Kustagi, M., Rügheimer, F., Califano, A. & Schwikowski, B. The Cyni framework for network inference in Cytoscape. Bioinformatics 31, 1499–1501 (2015).
Benjamini, Y., Krieger, A.M. & Yekutieli, D. Adaptive linear step-up procedures that control the false discovery rate. Biometrika 93, 491–507 (2006).
Cokelaer, T. et al. DREAMTools: a Python package for scoring collaborative challenges. F1000Research 4, 1030 (2015).
Acknowledgements
P.T.S., S.M., G.B.M. and J.W.G. kindly provided the experimental data for this challenge before publication. We are grateful to the Heritage Provider Network for their support of the DREAM Challenge. This work was supported in part by the US National Institutes of Health (National Cancer Institute (NCI) grants U54 CA 112970 (to J.W.G.) and 5R01CA180778 (to J.M.S.), NCI award U54CA143869 to M.F.C. and National Institute of General Medical Sciences award 1R01GM109031 to J.M.S.), the Susan G. Komen Foundation (SAC110012 to J.W.G.), the Prospect Creek Foundation (grant to J.W.G.), the EuroinvesXgacion program of MICINN (Spanish Ministry of Science and InnovaXon), partners of the ERASysBio+ iniXaXve supported under the EU ERA-NET Plus Scheme in FP7 (SHIPREC), MICINN (FEDER BIO2008-0205, FEDER BIO2011-22568 and EUI2009-04018 to B.O.), the Royal Society (Wolfson Research Merit Award to S.M.), the German Federal Ministry of Education and Research GANI_MED Consortium (grant 03IS2061A to T.K.), and the US National Library of Medicine (grants R00LM010822 (to X.J.) and R01LM011663 (to X.J. and R.E.N.)). We thank P. Kirk for comments on the manuscript and D. Henriques for input into the post-challenge analysis of the in silico data set.
Author information
Authors and Affiliations
Consortia
Contributions
S.M.H., L.M.H., T.C., M.U., J.W.G., P.T.S., H.K., G.S., J.S.-R. and S.M. designed the challenge. J.W.G., P.T.S., N.K.N., G.B.M. and S.M. provided experimental data for use in the challenge. M.U. and H.K. provided data for the in silico data task. M.K., T.N. and S.F. developed and implemented the Synapse platform used to facilitate the challenge. S.M.H., L.M.H. and T.C. performed analyses of challenge data. S.M.H., L.M.H., T.C., M.U., H.K., G.S., J.S.-R. and S.M. interpreted the results of the challenge. D.E.C. and Y.Z. performed analyses to compare top-performing approaches submitted for the network inference sub-challenge. D.E.C., A.S., E.O.P., C.K.W., K.G., A.B. and J.M.S. designed the top-performing approach in the experimental data network inference task. Y.Z., H.W. and M.S. designed the approach that performed best in the in silico data network inference task and was the highest ranked across both experimental and in silico data network inference tasks. F.Z. and Y.G. developed an algorithm that was a top performer in the experimental data time-course prediction task and was also the highest ranked across both experimental and in silico data time-course prediction tasks. B.A., L.V.D., A.V.F., W.S.L., D.T. and E.J.F. were members of one of the top-performing teams in the experimental data time-course prediction task. C.W.H., B.L.L., D.P.N., A.J.B. and A.A.Q. designed the Biowheel visualization tool. The HPN-DREAM Consortium provided predictions and descriptions of the algorithms. S.M.H., L.M.H., T.C., M.U., D.E.C., Y.Z., M.S., J.M.S., H.K., G.S., J.S.-R. and S.M. wrote the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
COMPETING FINANCIAL INTERESTS
The authors declare no competing financial interests.
Integrated supplementary information
Supplementary Figure 1 The HPN-DREAM network inference challenge: overview of in silico data tasks.
Data were generated from a nonlinear dynamical model of the ErbB signaling pathway (Chen et al., 2009). Training data consisted of time-courses for 20 network nodes under three inhibitors targeting specific nodes, or no inhibitor, and under two ligand stimuli, applied individually and in combination at two concentrations. In total there were 20 different (inhibitor, stimulus) conditions as shown (top right). Time-courses comprised 11 time points and three technical replicates were provided. Node names were anonymized to prevent use of biological prior information. The sub-challenge 1 in silico data task (SC1B) asked participants to infer a single directed, weighted network using the training data. The aim of the sub-challenge 2 in silico data task (SC2B) was to predict stimulus-specific time-courses under unseen interventions. For SC1B, submissions were assessed against a gold-standard network extracted from the data-generating model, with agreement quantified using AUROC score. For SC2B, predicted time-courses were assessed using held-out test data obtained under in silico inhibition of each network node in turn, with prediction accuracy quantified using root mean square error (RMSE). See Online Methods for further details of the in silico data tasks.
Chen, W.W. et al. Input-output behavior of ErbB signaling pathways as revealed by a mass action model trained against dynamic data. Mol. Syst. Biol. 5, 239 (2009).
Supplementary Figure 2 Context-specific ‘gold-standard’ causal descendant sets for the network inference sub-challenge experimental data task (SC1A).
Context-specific networks submitted to SC1A were assessed using held-out test data, obtained under inhibition of mTOR. Each column in the heatmap indicates, for a given (cell line, stimulus) context c, the phosphoproteins that showed salient changes under mTOR inhibition relative to DMSO control (black cells) and those that did not (white cells). Such changes were determined from the test data using a procedure centered around a paired t-test. Phosphoproteins that show salient changes can be regarded as descendants of mTOR in the underlying causal signaling network. Columns therefore represent context-specific experimentally-determined sets of causal descendants of mTOR, DcGS, and were used as a ‘gold-standard’ to assess inferred context-specific networks. Further details regarding the determination of the gold-standard descendant sets and the scoring procedure can be found in Online Methods. Missing data is indicated by gray cells (some phosphoprotein antibodies were only present in the (training and test) data for a subset of cell lines). Based on a figure in Hill, Nesser et al. (2016).
Hill, S.M., Nesser, N.K. et al. Context-specificity in causal signaling networks revealed by phosphoprotein profiling. bioRxiv doi:10.1101/039636 (2016).
Supplementary Figure 3 Network inference sub-challenge (SC1) final team scores and rankings.
(a) Mean rank scores for the 74 teams that participated in the experimental data task (SC1A). Mean rank scores were used to obtain final team rankings. For the 40 teams that provided information regarding their approach, bar color indicates method type (see also Fig. 3e, Supplementary Table 2 and Supplementary Note 5). Stars above bars indicate teams with statistically significant AUROC scores (FDR < 0.05) in at least 50% of (cell line, stimulus) contexts (2 stars) or at least 25% of contexts (1 star) (multiple testing correction performed within each context with respect to number of teams). (b) AUROC scores for the 65 teams that participated in the in silico data task (SC1B). AUROC scores were used to obtain final team rankings. As in a, color indicates method type (see also Fig. 3f, Supplementary Table 2 and Supplementary Note 5). Stars above bars indicate statistically significant AUROC scores (FDR < 0.05). (c) Comparison of mean rank and mean AUROC scores for SC1A. (d) Final ranks for SC1A (dashed blue line) and SC1B (dotted green line) were averaged to obtain a combined score (solid red line) for the 59 teams that participated in both tasks. Teams ordered by combined score (see “SC1A/B combined final rank” column in Supplementary Table 2). See Online Methods for full details of scoring for SC1.
Supplementary Figure 4 Gold-standard causal network for the network inference sub-challenge in silico data task (SC1B).
The gold-standard network, used to assess networks submitted to SC1B, was obtained from a data-generating dynamical model of the ErbB signaling pathway. Derivation of the network was non-trivial due to variables appearing in complexes within the model and full details can be found in Supplementary Note 8. Three unconnected dummy nodes were incorporated in the model and node names were anonymized in the training data.
Supplementary Figure 5 Balance of positives and negatives in the gold-standards for the network inference sub-challenge (SC1).
The gold standard for the experimental data task (SC1A) comprised sets of descendants of mTOR for each (cell line, stimulus) context, experimentally-determined using the held-out test data. Shown (left) are the number of positives and negatives for each context; that is, the number of phosphoproteins that are descendants of mTOR according to the test data (positives) and the number that are non-descendants of mTOR (negatives). For the in silico data task (SC1B), the gold-standard consisted of the data-generating network. Shown (right) are the number of edges in this network (positives) and the number of non-edges (negatives).
Supplementary Figure 6 Comparison of AUROC with an alternative scoring metric, AUPR, for the network inference sub-challenge (SC1).
(a) Alternative team rankings were calculated by replacing AUROC with AUPR (area under the precision-recall curve) in the scoring procedure. The alternative rankings were compared with the original AUROC-based rankings for both the experimental data task (SC1A; left) and in silico data task (SC1B; right). (b) A further alternative ranking, combining both AUROC and AUPR, was obtained by ranking teams based on an average of final rank under AUROC and final rank under AUPR, and was compared with the original AUROC-based rankings.
Supplementary Figure 7 Statistical significance of AUROC scores for the network inference sub-challenge experimental data task (SC1A).
For each (cell line, stimulus) context, a null distribution over AUROC was generated and used to calculate an FDR-adjusted P value for each team (Online Methods). (a) The number of significant (FDR < 0.05) AUROC scores obtained by each team across the 32 contexts (multiple testing correction performed within each context with respect to number of teams). Teams are ordered according to their final ranking in SC1A (based on mean rank score). (b) For each context, the number of teams (out of a total of 74) that obtained significant AUROC scores. For two regimes (BT549, NRG1) and (BT20, Insulin), no teams obtained a significant AUROC score. These two regimes were disregarded in the scoring process.
Supplementary Figure 8 Crowdsourced analysis for the network inference sub-challenge in silico data task (SC1B).
(a) Aggregate submission networks were formed by integrating predicted networks across the top N teams (as given by final team rankings), with N varied between 1 (top performer only) and all teams (after removal of correlated submissions; Supplementary Note 10). Integration was done by averaging predicted edge weights (Online Methods). The blue line shows performance (AUROC) of the aggregate submission networks. Individual team scores are also depicted (red circles). (b) Predicted networks were integrated for subsets of N teams, selected at random. The blue line shows mean performance of the aggregate submission networks, calculated over 100 random subsets of teams (error bars indicate s.d.). Crowdsourced analysis for the experimental data network inference task is shown in Figure 3c,d.
Supplementary Figure 9 Weighted combinations of two top performing approaches and aggregate prior network for the network inference sub-challenge experimental data task (SC1A).
An extension of Figure 4b to show three-way combinations of (i) PropheticGranger – top performer for the experimental data task when combined with a prior network (here, the method is used without the prior network); (ii) FunChisq – top performer for the in silico data task and most consistent performer across both data types; and (iii) an aggregate prior network formed by integrating prior networks used by participants (Online Methods). The three approaches were combined by taking weighted averages of predicted edge scores for each (cell line, stimulus) context and performance assessed using mean AUROC. For example, the best performance (mean AUROC = 0.82) was achieved by combining 20% PropheticGranger, 50% FunChisq and 30% aggregate prior network, and is highlighted with an “X”. See Supplementary Note 1 for full details of the PropheticGranger and FunChisq approaches.
Supplementary Figure 10 Time-course prediction sub-challenge experimental data task (SC2A): phosphoproteins showing the largest changes under mTOR inhbition are predicted with least accuracy.
SC2A tasked participants with predicting phosphoprotein time-courses for each (cell line, stimulus) context under an unseen intervention (mTOR inhibition - mTORi). Submitted predictions were assessed against held-out test data obtained under mTORi. For each team, root mean square error (RMSE) scores were calculated for each (cell line, phosphoprotein) pair (see Supplementary Note 6). (a) Left: for each (cell line, phosphoprotein) pair, normalized RMSE1 for the top-ranked team (Team44) vs. absolute effect size. The effect size for a given (cell line, phosphoprotein) pair is a measure of the magnitude of abundance change under mTORi relative to DMSO control2. Note that this measure is based on the mTORi test data and is independent of team predictions. The strong positive correlation indicates that phosphoproteins showing little or no change under mTORi were predicted relatively well but phosphoproteins that showed large changes under mTORi were predicted badly. Right: examples of time-courses underlying the scatter plot (left). Shown are abundances of three phosphoproteins for cell line UACC812 under DMSO control and under mTORi, as predicted by Team44 and test data values. Note that normalized RMSE and effect size values are calculated across all stimuli, but only serum stimulus time-courses are shown here. (b) Scatter plots as in a for teams ranked 2 to 5 in SC2A. These results highlight the challenging nature of predicting protein abundance under unseen interventions but also point to a shortcoming of the RMSE score used here, namely that it does not sufficiently emphasize ability to predict proteins that change under intervention. For a future challenge, a modified metric that focuses on those proteins might therefore be useful.
1To ensure comparability across cell lines and phosphoproteins, each RMSE score was normalized by the standard deviation of the test data used in the RMSE calculation. 2Effect size is defined as the mean difference in phosphoprotein abundance between DMSO control and mTORi, normalized by the standard deviation of the differences. Means and standard deviations are calculated across all time points and stimuli for the given cell line.
Supplementary Figure 11 Visualization sub-challenge (SC3) voting results and rankings.
14 teams made submissions to the visualization sub-challenge. HPN-DREAM challenge participants were asked to select and rank (from 1 to 3) their three favorite submissions. The remaining unranked submissions were then assigned a rank of 4. Thirty-six participants participated in the voting process and the number of votes of each rank type is shown (bar plot, left axis). Final team ranks were based on the mean rank across the 36 votes (green line, right axis).
Supplementary Figure 12 Robustness of rankings for the network inference sub-challenge (SC1).
The test data was subsampled to assess robustness of rankings (Online Methods). Box plots show team ranks over 100 subsampling iterations, with 50% of the test data left out at each iteration. (a) Experimental data task - subsampling performed by removing 50% of phosphoproteins when assessing descendant sets for each (cell line, stimulus) context. (b) Experimental data task – subsampling performed by removing 50% of contexts from the scoring process. (c) In silico data task – subsampling performed by considering only 50% of edges/non-edges in the gold-standard network. For all box plots, the central line indicates the median, and the box edges denote the 25th and 75th percentiles. Whiskers extend to 1.5 times the interquartile range from the box hinge. Data points beyond the whiskers are regarded as outliers and are plotted individually.
Supplementary information
Supplementary Text and Figures
Supplementary Figures 1–12 and Supplementary Notes 1–11 (PDF 8568 kb)
Supplementary Table 1
List of antibodies. (XLSX 18 kb)
Supplementary Table 2
Network inference sub-challenge (SC1) results, metadata, and inclusion of teams in Consortium and post-challenge analyses. (XLSX 40 kb)
Supplementary Table 3
Comparison of aggregate submission networks with the aggregate prior network to identify novel, context-specific edges. (XLSX 137 kb)
Supplementary Table 4
Time-course prediction sub-challenge (SC2) results, metadata, and inclusion of teams in Consortium. (XLSX 18 kb)
Supplementary Table 5
(Cell line, phosphoprotein) pairs disregarded in the scoring procedure for the time-course prediction sub-challenge experimental data task (SC2A). (XLSX 11 kb)
Supplementary Table 6
(Test inhibitor, predicted node) pairs disregarded in the scoring procedure for the time-course prediction sub-challenge in silico data task (SC2B). (XLSX 12 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. The images or other third party material in this article are included in the article's Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/.
About this article
Cite this article
Hill, S., Heiser, L., Cokelaer, T. et al. Inferring causal molecular networks: empirical assessment through a community-based effort. Nat Methods 13, 310–318 (2016). https://doi.org/10.1038/nmeth.3773
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nmeth.3773
This article is cited by
-
EnsInfer: a simple ensemble approach to network inference outperforms any single method
BMC Bioinformatics (2023)
-
Deep learning of causal structures in high dimensions under data limitations
Nature Machine Intelligence (2023)
-
Improved baselines for causal structure learning on interventional data
Statistics and Computing (2023)
-
Data-driven learning how oncogenic gene expression locally alters heterocellular networks
Nature Communications (2022)
-
Analysis of the first genetic engineering attribution challenge
Nature Communications (2022)