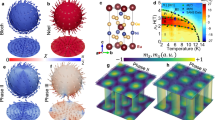
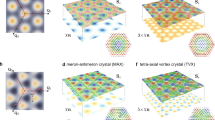
Abstract
Following the early prediction of the skyrmion lattice (SkL)—a periodic array of spin vortices—it has been observed recently in various magnetic crystals mostly with chiral structure. Although non-chiral but polar crystals with Cnv symmetry were identified as ideal SkL hosts in pioneering theoretical studies, this archetype of SkL has remained experimentally unexplored. Here, we report the discovery of a SkL in the polar magnetic semiconductor GaV4S8 with rhombohedral (C3v) symmetry and easy axis anisotropy. The SkL exists over an unusually broad temperature range compared with other bulk crystals and the orientation of the vortices is not controlled by the external magnetic field, but instead confined to the magnetic easy axis. Supporting theory attributes these unique features to a new Néel-type of SkL describable as a superposition of spin cycloids in contrast to the Bloch-type SkL in chiral magnets described in terms of spin helices.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 12 print issues and online access
$259.00 per year
only $21.58 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Bogdanov, A. N. & Yablonskii, D. A. Thermodynamically stable ‘vortices’ in magnetically ordered crystals. The mixed state of magnets. Zh. Eksp. Teor. Fiz. 95, 178–182 (1989).
Bogdanov, A. N. & Yablonskii, D. A. Contribution to the theory of inhomogeneous states of magnets in the region of magnetic-field-induced phase transitions. Mixed state of antiferromagnets. Zh. Eksp. Teor. Fiz. 96, 253–260 (1989).
Bogdanov, A. N. & Hubert, A. Thermodynamically stable magnetic vortex states in magnetic crystals. J. Magn. Magn. Mater. 138, 255–269 (1994).
Bogdanov, A. N. & Hubert, A. The properties of isolated magnetic vortices. Phys. Status Solidi b 186, 527–543 (1994).
Rössler, U. K., Bogdanov, A. N. & Pfleiderer, C. Spontaneous skyrmion ground states in magnetic metals. Nature 422, 797–801 (2006).
Leonov, A. Twisted, Localized, and Modulated States Described in the Phenomenological Theory of Chiral and Nanoscale Ferromagnets PhD thesis (2014); http://nbn-resolving.de/urn:nbn:de:bsz:14-qucosa-83823
Mühlbauer, S. et al. Skyrmion lattice in a chiral magnet. Science 323, 915–919 (2009).
Münzer, W. et al. Skyrmion lattice in the doped semiconductor Fe1−xCoxSi. Phys. Rev. B 81, 041203(R) (2010).
Yu, X. Z. et al. Real-space observation of a two-dimensional skyrmion crystal. Nature 465, 901–904 (2010).
Yu, X. Z. et al. Near room-temperature formation of a skyrmion crystal in thin-films of the helimagnet FeGe. Nature Mater. 10, 106–109 (2011).
Wilhelm, H. et al. Precursor phenomena at the magnetic ordering of the cubic helimagnet FeGe. Phys. Rev. Lett. 107, 127203 (2011).
Seki, S., Yu, X. Z., Ishiwata, S. & Tokura, Y. Observation of skyrmions in a multiferroic material. Science 336, 198–201 (2012).
Adams, T. et al. Long-wavelength helimagnetic order and skyrmion lattice phase in Cu2OSeO3 . Phys. Rev. Lett. 108, 237204 (2012).
Tonomura, A. et al. Real-space observation of skyrmion lattice in helimagnet MnSi thin samples. Nano Lett. 12, 1673–1677 (2012).
Milde, P. et al. Unwinding of a skyrmion lattice by magnetic monopoles. Science 340, 1076–1080 (2013).
Shibata, K. et al. Towards control of the size and helicity of skyrmions in helimagnetic alloys by spin–orbit coupling. Nature Nanotech. 8, 723–728 (2013).
Park, H. S. et al. Observation of the magnetic flux and three dimensional structure of skyrmion lattices by electron holography. Nature Nanotech. 9, 337–342 (2014).
Wilson, M. N. et al. Extended elliptic skyrmion gratings in epitaxial MnSi thin films. Phys. Rev. B 86, 144420 (2012).
Wilson, M. N. et al. Chiral skyrmions in cubic helimagnet films: The role of uniaxial anisotropy. Phys. Rev. B 89, 094411 (2014).
Ta Phouc, V. et al. Optical conductivity measurements of GaTa4Se8 under high pressure: Evidence of a bandwidth-controlled insulator-to-metal Mott transition. Phys. Rev. Lett. 110, 037401 (2013).
Abd-Elmeguid, M. M. et al. Transition from Mott insulator to superconductor in GaNb4Se8 and GaTa4Se8 under high pressure. Phys. Rev. Lett. 93, 126403 (2004).
Dorolti, E. et al. Half-metallic ferromagnetism and large negative magnetoresistance in the new lacunar spinel GaTi3VS8 . J. Am. Chem. Soc. 132, 5704–5710 (2010).
Kim, H.-S., Im, J., Han, M. J. & Jin, H. Spin-orbital entangled molecular jeff states in lacunar spinel compounds. Nature Commun. 5, 3988 (2014).
Guiot, V. et al. Avalanche breakdown in GaTa4Se8−xTex narrow-gap Mott insulators. Nature Commun. 4, 1722 (2013).
Singh, K. et al. Orbital-ordering-driven multiferroicity and magnetoelectric coupling in GeV4S8 . Phys. Rev. Lett. 113, 137602 (2014).
Pocha, R., Johrendt, D. & Pöttgen, R. Electronic and structural instabilities in GaV4S8 and GaMo4S8 . Chem. Mater. 12, 2882–2887 (2000).
Ruff, E. et al. Ferroelectric skyrmions and a zoo of multiferroic phases in GaV4S8. Preprint at http://xxx.lanl.gov/abs/1504.00309 (2015)
Okamoto, Y., Nilsen, G. J., Attfield, J. P. & Hiroi, Z. Breathing pyrochlore lattice realized in A-site ordered spinel oxides LiGaCr4O8 and LiInCr4O8 . Phys. Rev. Lett. 110, 097203 (2013).
Kimura, K., Nakatsuji, S. & Kimura, T. Experimental realization of a quantum breathing pyrochlore antiferromagnet. Phys. Rev. B 90, 060414(R) (2014).
Yadav, C. S., Nigam, A. K. & Rastogi, A. K. Thermodynamic properties of ferromagnetic Mott-insulator GaV4S8 . Physica B 403, 1474–1475 (2008).
Nakamura, H. et al. Low-field multi-step magnetization of GaV4S8 single crystal. J. Phys. Conf. Ser. 145, 012077 (2009).
Thessieu, C., Pfleiderer, C., Stepanov, A. N. & Flouquet, J. Field dependence of the magnetic quantum phase transition in MnSi. J. Phys. Condens. Matter 9, 6677–6687 (1997).
Lamago, D., Georgii, R., Pfleiderer, C. & Böni, P. Magnetic-field induced instability surrounding the A-phase of MnSi: Bulk and SANS measurements. Physica B 385–386, 385–387 (2006).
Pfleiderer, C. et al. Skyrmion lattices in metallic and semiconducting B20 transition metal compounds. J. Phys. Condens. Matter 22, 164207 (2010).
Adams, T. et al. Long-range crystalline nature of the skyrmion lattice in MnSi. Phys. Rev. Lett. 107, 217206 (2011).
Bak, P. & Jensen, M. H. Theory of helical magnetic structures and phase transitions in MnSi and FeGe. J. Phys. C: Solid State Phys. 13, L881–L885 (1980).
White, J. S. et al. Electric-field-induced skyrmion distortion and giant lattice rotation in the magnetoelectric insulator Cu2OSeO3 . Phys. Rev. Lett. 113, 107203 (2014).
Dzyloshinskii, I. E. Theory of helicoidal structures in antiferromagnets. I. Nonmetals. Sov. Phys. JETP 19, 960–971 (1964).
Heinze, S. et al. Spontaneous atomic-scale magnetic skyrmion lattice in two dimensions. Nature Phys. 7, 713–718 (2011).
Romming, N. et al. Writing and deleting single magnetic skyrmions. Science 341, 636–639 (2013).
Romming, N., Kubetzka, A., Hanneken, C., von Bergmann, K. & Wiesendanger, R. Field-dependent size and shape of single magnetic skyrmions. Phys. Rev. Lett. 114, 177203 (2015).
Fert, A., Cros, V. & Sampaio, J. Skyrmions on the track. Nature Nanotech. 8, 152–156 (2013).
Sampaio, J., Cros, V., Rohart, S., Thiaville, A. & Fert, A. Nucleation, stability and current-induced motion of isolated magnetic skyrmions in nanostructures. Nature Nanotech. 8, 839–844 (2013).
Mochizuki, M. et al. Thermally driven ratchet motion of a skyrmion microcrystal and topological magnon Hall effect. Nature Mater. 13, 241–246 (2014).
Acknowledgements
We thank H. A. K. V. Nidda and T. Fehér for useful discussions. This work was supported by the Hungarian Research Funds OTKA K 108918, OTKA PD 111756 and Bolyai 00565/14/11, by the European Research Council Project CONQUEST, by the Swiss NSF Grant Nos. 153451, 146870 and 141962, by the DFG under Grant No. SFB 1143 and via the Transregional Research Collaboration TRR 80 From Electronic Correlations to Functionality (Augsburg/Munich/Stuttgart) and by JSPS KAKENHI under Grant Nos. 25870169 and 25287088 from MEXT Japan.
Author information
Authors and Affiliations
Contributions
I.K., S.B., P.M., E.N., L.M.E., J.S.W., C.D.D., D.E. and V.T. performed the measurements; I.K., S.B., P.M., E.N., H.M.R., J.S.W. and A.L. analysed the data; V.T. and H.N. contributed to the sample preparation; M.M. and K.Y. developed the theory; I.K. wrote the manuscript and planned the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Information (PDF 998 kb)
Rights and permissions
About this article
Cite this article
Kézsmárki, I., Bordács, S., Milde, P. et al. Néel-type skyrmion lattice with confined orientation in the polar magnetic semiconductor GaV4S8. Nature Mater 14, 1116–1122 (2015). https://doi.org/10.1038/nmat4402
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nmat4402
This article is cited by
-
Dzyaloshinskii-Moriya interactions, Néel skyrmions and V4 magnetic clusters in multiferroic lacunar spinel GaV4S8
npj Computational Materials (2024)
-
Discovery of strong bulk Dzyaloshinskii-Moriya interaction in composition-uniform centrosymmetric magnetic single layers
Science China Physics, Mechanics & Astronomy (2024)
-
Stabilization and racetrack application of asymmetric Néel skyrmions in hybrid nanostructures
Scientific Reports (2023)
-
When Ising met Kibble–Zurek
Nature Physics (2023)
-
Resonating holes vs molecular spin-orbit coupled states in group-5 lacunar spinels
Nature Communications (2023)