Abstract
Pairing in an attractively interacting two-component Fermi gas in the absence of time-reversal symmetry or inversion symmetry may give rise to exotic superfluid states. Notable examples range from the Fulde–Ferrell–Larkin–Ovchinnikov state with a finite centre-of-mass momentum in a polarized Fermi gas to the topological superfluid (TSF) state in a two-dimensional (2D) Fermi gas under Rashba spin–orbit coupling and an out-of-plane Zeeman field. Here we show that a TSF state with a single-component nonzero centre-of-mass momentum, called a topological Fulde–Ferrell (tFF) state, can be stabilized in a 2D Fermi gas with Rashba spin–orbit coupling and both in-plane and out-of-plane Zeeman fields. The tFF state features a non-trivial Berry phase, along with unique properties that may be detected using existing experimental techniques.
Similar content being viewed by others
Introduction
Since their original proposal in the 1906s, unconventional pairing states with finite centre-of-mass momentum have caught a considerable amount of attention in different physical contexts1,2,3, including organic superconductors4, heavy fermions5 and dense quark matter6. Initially proposed as a compromise between superconductivity and finite magnetization, the key ingredient of this so-called Fulde–Ferrell–Larkin–Ovchinnikov (FFLO) state is a pairing mechanism between fermions having a finite centre-of-mass momentum. In the weak-coupling limit, this can be achieved by pairing particles residing either on distinct Fermi surfaces, as in the case of spin-polarized systems where spin-up and spin-down Fermi surfaces are mismatched, or on a single deformed Fermi surface which breaks the spatial inversion symmetry. The latter possibility has been discussed in the context of non-centrosymmetric superconductors, where spin–orbit coupling (SOC) of the Rashba (σxkx+σyky) or the Dresselhaus type (σxkx−σyky) would lead to a non-uniform superconducting state under external magnetic fields7,8,9,10,11. Here, σi are the Pauli matrices and ki is the ith (i=x, y, z) component of the single-particle momentum.
In ultracold Fermi gases, the pursuit of FFLO states has stimulated extensive investigation almost immediately after the realization of pairing superfluidity12. Recently, evidence for the FFLO superfluid has been reported in quasi-one-dimensional geometry at Rice Univeristy13. Meanwhile, the realization of synthetic SOC adds another important piece to the already versatile toolbox of controllability in cold atoms14,15,16,17. By Raman-coupling two hyperfine states in the ground state manifold of alkali atoms, experimentalists have implemented an equal mixture of Rashba and Dresselhaus SOC with both out-of-plane and in-plane effective Zeeman fields. In these experiments, the SOC strength depends on the wave vectors of the Raman lasers, and the effective out-of-plane (in-plane) Zeeman field is proportional to the Rabi frequency (two-photon detuning) of the Raman process. Theoretical investigation has demonstrated that the interplay of SOC, pairing superfluidity and effective Zeeman fields can lead to exotic superfluid phases in various dimensions18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41. In these systems, as SOC mixes different spin states, both intra- and inter-branch pairings can take place and the competition between them results in rich phase structures. An important example here is the topological superfluid (TSF) state in a two-dimensional (2D) Fermi gas with Rashba SOC and an out-of-plane Zeeman field27. The TSF state acquires a chiral Majorana edge mode protected by the gap in the bulk, and can be understood in the weak-coupling limit as a consequence of intra-branch pairing when the chemical potential lies within or below the gap opened by the out-of-plane Zeeman field. As both the inversion and the time-reversal symmetries are broken in the system, the TSF state belongs to class D.
In this work, we show that a TSF state with a single-component nonzero centre-of-mass momentum, that is, a topological Fulde–Ferrell (tFF) state, can be stabilized in a 2D Fermi gas with Rashba SOC and both in-plane and out-of-plane Zeeman fields. Similar to the case of a TSF state, in the weak-coupling limit, the emergence of the tFF state can be understood as a result of single-branch pairing within the lower helicity branch. The application of the additional in-plane Zeeman field introduces deformation of the single-particle dispersion, and drives the system towards a more stable Fulde–Ferrell (FF) state. The resulting pairing state would preserve all topological properties provided that the deformation of the Fermi surface should not be drastic enough to violate the single-branch pairing scenario. This last condition is equivalent to the requirement that the introduction of the in-plane Zeeman field should not close the bulk gap. Thus, the topological nature of this state is protected by a full gap of quasi-particle spectra. This tFF state belongs to the same classification as that of the TSF state found in 2D Fermi gases with Rashba SOC27, and acquires all topological features including gapless edge states and Majorana zero modes in vortex cores42. We note that the centre-of-mass momentum of this tFF state is antiparallel to the in-plane Zeeman field. By mapping out the zero-temperature phase diagram, we further discuss the competition between various FF states with different centre-of-mass momentum. In particular, we find a nodal FF (nFF) state and characterize the evolution of its non-trivial gapless contours in momentum space. The tFF and nFF states should leave signatures in the species-selective momentum distribution and momentum-resolved radio-frequency spectroscopy, respectively, which, in principle, can be detected using existing experimental techniques.
Results
Phase diagram and the tFF state
We consider a two-component Fermi gas in two dimensions with a Rashba SOC and both in-plane and out-of-plane Zeeman fields, where the Hamiltonian can be written as follows:

Here, ξk=εk–μ, εk=ħ2k2/2m, ak σ ( ) is the annihilation (creation) operator for the pseudo-spin state σ with σ=(↑, ↓), m is the atomic mass, α denotes the strength of the SOC and HC stands for Hermitian conjugate. The out-of-plane (h) and in-plane (hx) Zeeman fields can be effectively induced depending on how the synthetic SOC is implemented. As an example, h and hx are proportional to the effective Rabi frequency and the two-photon detuning, respectively, of the Raman process in the current experimental scheme15,16. The bare s-wave interaction rate U should be renormalized as43:
) is the annihilation (creation) operator for the pseudo-spin state σ with σ=(↑, ↓), m is the atomic mass, α denotes the strength of the SOC and HC stands for Hermitian conjugate. The out-of-plane (h) and in-plane (hx) Zeeman fields can be effectively induced depending on how the synthetic SOC is implemented. As an example, h and hx are proportional to the effective Rabi frequency and the two-photon detuning, respectively, of the Raman process in the current experimental scheme15,16. The bare s-wave interaction rate U should be renormalized as43:  , where is the quantization area, and Eb is the binding energy of the two-body bound state in two dimensions without SOC, which can be tuned, for instance, via the Feshbach resonance technique44. We focus on the zero-temperature properties of the system on the mean-field level, where the pairing order parameter
, where is the quantization area, and Eb is the binding energy of the two-body bound state in two dimensions without SOC, which can be tuned, for instance, via the Feshbach resonance technique44. We focus on the zero-temperature properties of the system on the mean-field level, where the pairing order parameter  , with Q the center-of-mass momentum of the pairing states.
, with Q the center-of-mass momentum of the pairing states.
For pairing states with zero centre-of-mass momentum (Q=0), analytical form of the dispersion spectrum can be obtained in the absence of the in-plane Zeeman field (hx=0)27. In this case, a fully gapped TSF can be stabilized in a fairly large parameter region. The topological nature of this phase is characterized by a non-trivial topological number, and is protected by the underlying particle-hole symmetry. For the case of hx≠0, it can be proved that the zero centre-of-mass momentum state becomes unstable against an FF state with pairing momentum  . Thus, a topologically non-trivial FF state can be expected, provided that the in-plane field should not be large enough to close the gap of the bulk.
. Thus, a topologically non-trivial FF state can be expected, provided that the in-plane field should not be large enough to close the gap of the bulk.
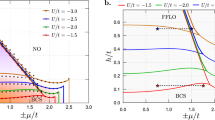
To characterize the stability region of the tFF state, we map out the phase diagram on the plane of the SOC strength (α) and the chemical potential (μ), with fixed out-of-plane Zeeman field h and finite hx (Fig. 1). Under the local density approximation, the phases traversed by a downward vertical line in the diagram represent those one should encounter by moving from a trap centre to its edge. From Fig. 1, we see that the TSF phase in a 2D polarized Fermi gas with Rashba SOC and zero in-plane field is now replaced by a tFF phase with centre-of-mass momentum along the x-direction, as we have anticipated. To characterize the non-trivial topological nature of this state, we further calculate the Berry phases associated with the two quasi-particle (η=+, ν=1, 2) and two quasi-hole (η=−, ν=1, 2) bands:
(a–c) Illustration of pairing mechanisms that give rise to different phases in the weak-coupling limit: (a) intra-branch pairing with a single Fermi surface, (b) intra-branch pairing with two Fermi surfaces and (c) inter-branch pairing. The filled areas with different colours represent the Fermi surfaces in the lower and upper helicity branches, and the black dot represents the origin of the momentum space. (d) Phase diagrams on the α−μ plane for Eb/h=0.5 and hx/h=0.1, where Eb is the binding energy of the two-body bound state in two dimensions without SOC. The solid curves are first-order boundaries, whereas the dash-dotted curves represent phase boundaries of continuous phase transitions. The dashed curves surrounding the normal region (N) are the threshold with ΔQ/h=10−3, whereas the dotted curves are the boundary against vacuum (VAC). In the weak-coupling limit, the tFF state corresponds to the pairing mechanism (a), the gapped FF (gFF) state and the nFF state correspond to the pairing mechanism (b), while (c) gives rise to a parameter region on the phase diagram where the global ground state is the result of competition between different FF states with centre-of-mass momentum in the x- or the y-direction (mixed). The out-of-plane Zeeman field h is taken to be the unit of energy, whereas the unit of momentum kh is defined through  .
.

where the Berry curvature is defined as45

with  the shorthand notation. The Berry phase of the superfluid state is then a summation over the contribution
the shorthand notation. The Berry phase of the superfluid state is then a summation over the contribution  from the two occupied quasi-hole bands. A numerical evaluation shows that the resulting Berry phase vanishes in the topological trivial phase and becomes unity in the tFF state. As we have discussed before, the stabilization of the tFF state is due to the SOC-induced intra-branch pairing and the Fermi surface asymmetry.
from the two occupied quasi-hole bands. A numerical evaluation shows that the resulting Berry phase vanishes in the topological trivial phase and becomes unity in the tFF state. As we have discussed before, the stabilization of the tFF state is due to the SOC-induced intra-branch pairing and the Fermi surface asymmetry.
nFF states and topological phase transitions
The simple picture of single-branch pairing becomes complicated with increasing chemical potential or increasing SOC intensity, such that particles on the higher helicity branch get involved into pairing. Due to the spin mixing induced by the SOC, both intra- and inter-branch pairings can take place with centre-of-mass momentum along either the x- or the y-direction. As a consequence, the ground state of the system is the result of competitions between the various FF pairing states, leading to a variety of FF states as depicted in Fig. 1.
In the case of strong SOC intensity, or equivalently weak out-of-plane Zeeman field, the ground state of the system becomes a topologically trivial FF state (gFF in Fig. 1), which is separated from the tFF state via a continuous phase boundary. This gFF phase is also fully gapped and with centre-of-mass momentum along the x axis. In the weak-coupling limit, the gFF phase corresponds to an intra-branch pairing in the presence of two Fermi surfaces. By tuning through the tFF–gFF phase boundary, the excitation gap closes and opens again, while the pairing order parameter ΔQ remains finite. A typical variation of the minimum excitation gap Eg, the pairing order parameter ΔQ and the pairing momentum Qx with increasing chemical potential are plotted in Fig. 2a,b, respectively.
(a,b) Evolution of the minimum excitation gap (a), the order parameter (a:inset) and pairing momentum (b) with increasing chemical potential. A full gap closes and opens again by traversing the continuous phase boundary between the tFF state and the gFF state. In these subplots, hx/h=0.1. (c,d) Evolution of the minimum excitation gap and the pairing order parameter (insets) with increasing in-plane field hx, with: (c) μ/h=1 and (d) μ/h=0.8. Other parameters used in this figure are Eb/h=0.5 and αkh/h=1.
Besides the gFF state, intra-branch pairing with two Fermi surfaces may also lead to an nFF phase. Indeed, close to the tFF and the gFF states, we identify a region on the phase diagram where the ground state is an nFF phase with pairing momentum along the x-direction, as depicted in Fig. 1. This gapless superfluid state acquires two disconnected gapless contours in momentum space, which shrink to two separated gapless points and disappear at the continuous phase boundaries. A typical evolution of the two gapless contours are displayed in Fig. 3a with increasing chemical potential. In principle, these features can be reconstructed via momentum-resolved radio-frequency spectroscopy or Bragg spectroscopy. Notice that at the phase boundaries between the nFF and the gapped FF states (gFF or tFF), the quasi-particle and quasi-hole spectra touch the Fermi surface at different places (see Fig. 3c for example). This is in contrast to the phase boundary between the tFF and the gFF states, where the gap closes at a single point k=(Qx/2, 0) in momentum space (see Fig. 3d). Hence, the topological phase boundary between the tFF and the gFF states can be worked out by examining the gap closing condition
(a) Evolution of gapless contours in the momentum space for the nFF states with αkh/h=0.49, and μ/h=1.002 (magenta), 1.05 (blue) and 1.15 (black). (b–d) Dispersion spectra of quasi-particle and quasi-hole along the kx axis with (b) αkh/h=0.49, μ/h=1.05; (c) αkh/h=0.49, μ/h=1.002; and (d) αkh/h=0.8, μ/h=0.87. It is apparent from (c–d) that at the topological phase boundaries, two gapless points exist between the nFF and the tFF states, whereas a single gapless point exists between the gFF and the tFF states. Other parameters used in these plots are Eb/h=0.5 and hx/h=0.1.

On the other hand, the topological phase boundary between the nFF and the tFF states needs to be determined numerically.
Alternatively, the inter-branch pairing scenario can become significant with decreasing SOC intensity or increasing out-of-plane Zeeman field, which can effectively polarize the helices within each helicity branch and hence hinder intra-branch pairing. This gives rise to a parameter region on the phase diagram labelled as Mixed, where the global ground state is the result of competition between different FF states with centre-of-mass momentum in the x- or the y-direction. These states are typically very close in energy, and can be qualitatively understood as conventional FF states dressed by SOC.
The phase transitions between the various FF states, the topological ones in particular, can also be investigated by sweeping the in-plane Zeeman field hx. In the weak-coupling limit, the presence of a larger hx shifts the upper helicity branch and enlarges the gap between two branches. As a consequence, the tFF state, which is dominated by the intra-branch pairing within the lower helicity branch, becomes stable in an extended parameter region, and the phase boundaries surrounding the tFF state are shifted towards larger values of chemical potential and SOC intensity. In Fig. 2c,d, we show the variation of the minimum excitation gap and the pairing order parameter with increasing in-plane field hx, indicating the two representative evolution paths of the system from gFF to nFF and eventually to tFF (Fig. 2c), or from gFF directly to tFF (Fig. 2d), depending on the starting point on the phase diagram.
Finally, we note that although the various FF states discussed above acquire spatially modulating order parameters, we expect no supercurrent flow within the system. In fact, similar FFLO states under SOC have been investigated in the context of non-centrosymmetric superconductors, where explicit calculations in the weak-coupling limit gave zero supercurrent10,11.
Momentum distribution across the topological phase boundary
To characterize properties of the various phases on the phase diagram, we calculate their respective momentum distribution. In Fig. 4, we show the momentum profiles of the minority spin component for cases within the tFF region (a and b) and the gFF region (c and d). It is apparent that the momentum distribution in a topologically non-trivial phase is drastically different from that in a topologically trivial phase. In particular, the density profile in momentum space for the minority spin features a dip in the tFF phase, in contrast to a peak in the gFF case. These results can be qualitatively understood by noticing that in the weakly interacting limit, the tFF state corresponds to intra-branch pairing within the lower helicity branch, where the population of the minority fermions is small around the point where the spin-mixing term vanishes. Meanwhile, the gFF state corresponds to the case of intra-branch pairing with two Fermi surfaces, where a filled upper helicity branch implies a maximally occupied minority spin state around the same location.
The qualitative difference in momentum distribution of the minority fermions leads to an abrupt jump as the topological phase boundary is crossed. By extracting the momentum distribution from species-selective time-of-flight imaging, we may identify the tFF state in the underlying system.
Discussion
At present, only an equal mixture of Rashba and Dresselhaus SOC has been realized experimentally by Raman-coupling two hyperfine states in the ground state manifold of alkali atoms14,15,16. In these experiments, the effective Zeeman fields and the SOC strength are all dependent upon the laser parameters. This is also the case in most of the existing theoretical proposals for realizing Rashba SOC in ultracold atoms46,47. For instance, in ref. 47, Liu et al. proposed to implement Rashba SOC in a 2D Fermi gas trapped in a lattice potential. Although the SOC there relies on periodically modulated Raman fields, the out-of-plane and the in-plane Zeeman fields can be realized and tuned by introducing two-photon detuning in the Raman processes, and on-site fields which couple the hyperfine spins, respectively. Experimentally, the relevant parameters are typically on the order of the recoil energy Er, which is estimated to be 2πħ × 8.3 kHz in 40K atoms15. For a Raman process consisting of counter-propagating lasers, a moderate Rabi frequency of 8Er, and a small two-photon detuning of 0.8Er should lead to the parameters h~4Er, hx~0.4Er and αkh/h~1. For Eb=0.5h~2Er as chosen for Fig. 1, the tFF state can be stabilized over a considerable range of the chemical potential. We stress that these parameters can be further optimized. At finite temperatures, we expect that the tFF state be stable below the Berezinskii–Kosterlitz–Thouless transition temperature, which is on the order of 0.1TF for a 2D Fermi gas with SOC28,30. For a 2D Fermi gas without SOC, a temperature of T~0.27TF has recently been reported48. With these, it is reasonable to expect that the tFF state can be prepared and probed in future experiments.
To summarize, we have investigated the pairing states of a 2D Fermi gas with Rashba SOC and both in-plane and out-of-plane Zeeman fields. Our results indicate the stabilization of a tFF state with centre-of-mass momentum antiparallel to the direction of the in-plane field.
During the preparation of the final version of this article, we became aware of similar work by Qu et al., which also discusses the existence of a topological FFLO state in Fermi systems with spin-orbit coupling49.
Methods
Mean-field formalism
We focus on the zero-temperature properties of the FF pairing states with a single-valued centre-of-mass momentum on the mean-field level1,2. This should provide a qualitatively correct phase diagram at zero temperature. The effective mean field Hamiltonian can then be arranged into a matrix form in the hyperfine spin basis 

where Λk=α(kx+iky)−hx and the order parameter  . It is then straightforward to diagonalize the effective Hamiltonian and evaluate the thermodynamic potential at zero temperature
. It is then straightforward to diagonalize the effective Hamiltonian and evaluate the thermodynamic potential at zero temperature

where the quasi-particle (η=+) and quasi-hole (η=−) dispersions  (ν=1, 2) are the eigenvalues of the matrix in Hamiltonian (5), and Θ(x) is the Heaviside step function. Without loss of generality, we assume h, hx>0, and ΔQ to be real throughout the work. The pairing order parameter ΔQ as well as the centre-of-mass momentum Q for the pairs can then be found by minimizing the thermodynamic potential in equation (6). Note that in general, the Hamiltonian (5) cannot be diagonalized analytically, and the thermodynamic potential needs to be evaluated numerically.
(ν=1, 2) are the eigenvalues of the matrix in Hamiltonian (5), and Θ(x) is the Heaviside step function. Without loss of generality, we assume h, hx>0, and ΔQ to be real throughout the work. The pairing order parameter ΔQ as well as the centre-of-mass momentum Q for the pairs can then be found by minimizing the thermodynamic potential in equation (6). Note that in general, the Hamiltonian (5) cannot be diagonalized analytically, and the thermodynamic potential needs to be evaluated numerically.
Instability of the BCS state
In the presence of a finite in-plane Zeeman field, the Fermi surface is deformed. In this case, the SOC-induced intra-branch pairing leads to the stabilization of an FF state with finite centre-of-mass momentum. The instability of Bardeen–Cooper–Schrieffer (BCS) pairing in this case can be checked by an expansion of the thermodynamic potential around the BCS pairing state with respect to small centre-of-mass momentum Q=(Qx, 0)

where the expansion coefficients Ωi (i=0,1,2⋯) can be evaluated numerically. We find that for finite hx, the second-order expansion coefficient Ω2 is positive definite, whereas the first-order coefficient Ω1 is always nonzero and has an opposite sign to that of hx. Hence, the ground state of the system under finite hx is an FF state with the centre-of-mass momentum antiparallel to the in-plane Zeeman field. This can be further checked by explicit evaluations of the thermodynamic potential (see Fig. 5).
Additional information
How to cite this article: Zhang, W. and Yi, W. Topological Fulde–Ferrell–Larkin–Ovchinnikov states in spin–orbit-coupled Fermi gases. Nat. Commun. 4:2711 doi: 10.1038/ncomms3711 (2013).
References
Fulde, P. & Ferrell, R. A. Superconductivity in a strong spin-exchange field. Phys. Rev. 135, A550–A563 (1964).
Larkin, A. I. & Ovchinnikov, Y. N. Inhomogeneous state of superconductors. Sov. Phys. JETP 20, 762–769 (1965).
Casalbuoni, R. & Nardulli, G. Inhomogeneous superconductivity in condensed matter and QCD. Rev. Mod. Phys. 76, 263–320 (2004).
Ardavan, A. et al. Recent topics of organic superconductors. J. Phys. Soc. Jpn 81, 011004 (2012).
Radovan, H. A. et al. Magnetic enhancement of superconductivity from electron spin domains. Nature 425, 51–55 (2003).
Alford, M., Bowers, J. A. & Rajagopal, K. Crystalline color superconductivity. Phys. Rev. D 63, 074016 (2001).
Agterberg, D. F. Novel magnetic field effects in unconventional superconductors. Physica C 387, 13–16 (2003).
Samokhin, K. V. Magnetic properties of superconductors with strong spin-orbit coupling. Phys. Rev. B 70, 104521 (2004).
Kaur, R. P., Agterberg, D. F. & Sigrist, M. Helical vortex phase in the noncentrosymmetric CePt3Si. Phys. Rev. Lett. 94, 137002 (2005).
Dimitrova, O. & Feigel’man, M. V. Theory of a two-dimensional superconductor with broken inversion symmetry. Phys. Rev. B 76, 014522 (2007).
Michaeli, K., Potter, A. C. & Lee, P. A. Superconducting and ferromagnetic phases in SrTiO3/LaAlO3 oxide interface structures: possibility of finite momentum pairing. Phys. Rev. Lett. 108, 117003 (2012).
Radzihovsky, L. & Sheehy, D. E. Imbalanced Feshbach-resonant Fermi gases. Rep. Prog. Phys. 73, 076501 (2010).
Liao, Y. A. et al. Spin-imbalance in a one-dimensional Fermi gas. Nature 467, 567–569 (2010).
Lin, Y. J., Jiménez-García, K. & Speilman, I. B. Spin-orbit-coupled Bose-Einstein condensates. Nature 471, 83–86 (2011).
Wang, P. et al. Spin-Orbit coupled degenerate Fermi gases. Phys. Rev. Lett. 109, 095301 (2012).
Cheuk, L. W. et al. Spin-injection spectroscopy of a spin-orbit coupled Fermi gas. Phys. Rev. Lett. 109, 095302 (2012).
Zhang, J. Y. et al. Collective dipole oscillations of a spin-orbit coupled Bose-Einstein condensate. Phys. Rev. Lett. 109, 115301 (2012).
Zhang, C., Tewari, S., Lutchyn, R. M. & Das Sarma, S. p x+ip y superfluid from s-wave interactions of fermionic cold atoms. Phys. Rev. Lett. 101, 160401 (2008).
Sato, M., Takahashi, Y. & Fujimoto, S. Non-abelian topological order in s-wave superfluids of ultracold fermionic atoms. Phys. Rev. Lett. 103, 020401 (2009).
Vyasanakere, J. P., Zhang, S. & Shenoy, V. B. BCS-BEC crossover induced by a synthetic non-abelian gauge field. Phys. Rev. B 84, 014512 (2011).
Gong, M., Tewari, S. & Zhang, C. BCS-BEC crossover and topological phase transition in 3D spin-orbit coupled degenerate Fermi gases. Phys. Rev. Lett. 107, 195303 (2011).
Yu, Z. Q. & Zhai, H. Spin-orbit coupled Fermi gases across a Feshbach resonance. Phys. Rev. Lett. 107, 195305 (2011).
Hu, H., Liu, X. J. & Pu, H. Probing anisotropic superfluidity in atomic Fermi gases with Rashba spin-orbit coupling. Phys. Rev. Lett. 107, 195304 (2011).
Iskin, M. & Subasi, A. L. Stability of spin-orbit coupled Fermi gases with population imbalance. Phys. Rev. Lett. 107, 050402 (2011).
Yi, W. & Guo, G. C. Phase separation in a polarized Fermi gas with spin-orbit coupling. Phys. Rev. A 84, 031608(R) (2011).
Dell’Anna, L., Mazzarella, G. & Salasnich, L. Condensate fraction of a resonant Fermi gas with spin-orbit coupling in three and two dimensions. Phys. Rev. A 84, 033633 (2011).
Zhou, J., Zhang, W. & Yi, W. Topological superfluid in a trapped two-dimensional polarized Fermi gas with spin-orbit coupling. Phys. Rev. A 84, 063603 (2011).
Gong, M., Jia, S. & Zhang, C. Searching for Majorana fermions in 2D spin-orbit coupled Fermi superfluids at finite temperature. Phys. Rev. Lett. 109, 105302 (2012).
Han, L. & Sá de Melo, C. A. R. Evolution from BCS to BEC superfluidity in the presence of spin-orbit coupling. Phys. Rev. A 85, 011606(R) (2012).
He, L. & Huang, X. G. BCS-BEC crossover in 2D Fermi gases with Rashba spin-orbit coupling. Phys. Rev. Lett. 108, 145302 (2012).
Yang, X. & Wan, S. Phase diagram of a uniform two-dimensional Fermi gas with spin-orbit coupling. Phys. Rev. A 85, 023633 (2012).
Yi, W. & Zhang, W. Molecule and polaron in a highly polarized two-dimensional Fermi gas with spin-orbit coupling. Phys. Rev. Lett. 109, 140402 (2012).
Zheng, Z., Gong, M., Zou, X., Zhang, C. & Guo, G. C. Route to observable Fulde-Ferrell-Larkin-Ovchinnikov phases in 3D spin-orbit coupled degenerate Fermi gases. Phys. Rev. A 87, 031602(R) (2013).
Han, L. & Sá de Melo, C. A. R. Ultra-cold fermions in the flatland: evolution from BCS to Bose superfluidity in two-dimensions with spin-orbit and Zeeman fields. Preprint at http://arXiv.org/abs/1206.4984 (2012).
Iskin, M. & Subasi, A. L. Topological superfluid phases of an atomic Fermi gas with in- and out-of-plane Zeeman fields and equal Rashba-Dresselhaus spin-orbit coupling. Phys. Rev. A 87, 063627 (2013).
Wu, F., Guo, G. C., Zhang, W. & Yi, W. Unconventional superfluid in a two-dimensional Fermi gas with anisotropic spin-orbit coupling and Zeeman fields. Phys. Rev. Lett. 110, 110401 (2013).
Wu, F., Guo, G. C., Zhang, W. & Yi, W. Unconventional Fulde-Ferrell-Larkin-Ovchinnikov pairing states in a Fermi gas with spin-orbit coupling. Phys. Rev. A 88, 043614 (2013).
Zhou, X. F., Guo, G. C., Zhang, W. & Yi, W. Exotic pairing states in a Fermi gas with three-dimensional spin-orbit coupling. Phys. Rev. A 87, 063606 (2013).
Dong, L., Jiang, L. & Pu, H. Fulde-Ferrell pairing instability in spin-orbit coupled Fermi gas. New J. Phys. 15, 075014 (2013).
Iskin, M. Spin-orbit-coupling-induced Fulde-Ferrell-Larkin-Ovchinnikov-like Cooper pairing and skyrmion-like polarization textures in optical lattices. Phys. Rev. A 88, 013631 (2013).
Xu, Y., Qu, C., Gong, M. & Zhang, C. Competing superfluid orders in spin-orbit coupled fermionic cold atom optical lattices. Preprint at http://arXiv.org/abs/1305.2152 (2013).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Randeria, M., Duan, J. M. & Shieh, L. Y. Bound states, Cooper pairing, and Bose condensation in two dimensions. Phys. Rev. Lett. 62, 981–984 (1989).
Bloch, I., Dalibard, J. & Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 80, 885–964 (2008).
Xiao, D., Chang, M. C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959–2007 (2010).
Campbell, D. L., Juzeliunas, G. & Spielman, I. B. Realistic Rashba and Dressehaus spin-orbit coupling for neutral atoms. Phys. Rev. A 84, 025602 (2011).
Liu, X. J., Law, K. T. & Ng, T. K. Realization of 2D spin-orbit interaction and exotic topological orders in cold atoms. Preprint at http://arXiv.org/abs/1304.0291 (2013).
Feld, M., Fröhlich, B., Vogt, E., Koschorreck, M. & Köhl, M. Observation of a pairing pseudogap in a two-dimensional Fermi gas. Nature 480, 75–78 (2011).
Qu, C. et al. Topological superfluids with finite momentum pairing and Majorana fermions. Nat. Comm. (2013) doi:10.1038/ncomms3710 (in press).
Acknowledgements
We thank Hong Yao and Ying Ran for helpful discussions. This work is supported by NKBRP (2013CB922000), NFRP (2011CB921200, 2011CBA00200), NNSF (60921091), NSFC (11105134, 11274009), the Research Funds of Renmin University of China (10XNL016) and the Fundamental Research Funds for the Central Universities (WK2470000006).
Author information
Authors and Affiliations
Contributions
Both authors contributed equally to all parts of the work.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Zhang, W., Yi, W. Topological Fulde–Ferrell–Larkin–Ovchinnikov states in spin–orbit-coupled Fermi gases. Nat Commun 4, 2711 (2013). https://doi.org/10.1038/ncomms3711
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms3711
This article is cited by
-
Superconductivity in a ferroelectric-like topological semimetal SrAuBi
npj Quantum Materials (2023)
-
Vortex structure in spin–orbit-coupled spin-1 Bose gases with unequal atomic mass
Pramana (2022)
-
Spin-orbital-angular-momentum-coupled quantum gases
AAPPS Bulletin (2022)
-
Topological Larkin-Ovchinnikov phase and Majorana zero mode chain in bilayer superconducting topological insulator films
Communications Physics (2019)
-
Majorana fermions in semiconducting nanowire and Fulde–Ferrell superconductor hybrid structures
Frontiers of Physics (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

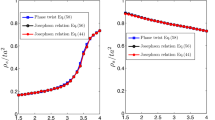




 and the chemical potentials are: (a) μ/h=−0.85, (b) μ/h=0.6977,(c) μ/h=0.6980 and (d) μ/h=1. Notice that the momentum distribution features a dip for the tFF state (a,b), and a peak for the gFF state (c,d).
and the chemical potentials are: (a) μ/h=−0.85, (b) μ/h=0.6977,(c) μ/h=0.6980 and (d) μ/h=1. Notice that the momentum distribution features a dip for the tFF state (a,b), and a peak for the gFF state (c,d).